基于多元统计分析的工资总额管控研究与应用

何丽

摘要：工资总额管控对于企业经济效益和提高企业职工工资水平等方面均有着重要意义，关乎整个企业职工的切身利益。为实现工资总额管控精细化以及预算方法多元化，科学有效地进行经济预测，寻求更多的创新思想和方法以做好管控工作，多方向进行预算比较，获得更为科学、有效、切合实际的工资总额预算数据。文章基于多元统计分析方法在工资总额管控方面的应用，并结合公司历史元素及变量因素对当前及未来工资总额管控的影响进行分析与研究。根据已知历史数据对短期未来数据进行规律探寻和建模分析，以更好地实现统计分析方法在工资总额管控方面的科学合理研究。

关键词：工资总额管控;工资总额预算;经济预测;多元统计分析;建模分析

工资总额管控对于企业经济效益和提高企业职工工资水平等方面均有着重要意义，关乎整个企业职工的切身利益。当前公司在工资总额预算管理方面存在预算变动频繁，相互制动的管控局面。有必要寻求多元统计分析方法对预算工作做进一步的管控研究。

为实现工资总额管控精细化以及预算方法多元化，科学有效地进行经济预测，有必要寻求更多的创新思想和方法以做好管控工作，多方向进行预算比较，获得更为科学、有效、切合实际的工资总额预算数据。基于多元统计分析方法，探索和研究该方法在工资总额管控方面的应用，能结合公司历史元素以及变量因素对当前及未来工资总额管控的影响进行分析与研究。能够基于已知历史数据对短期未来数据进行规律探寻和建模分析。以实现统计分析方法在工资总额管控方面的科学合理研究。

一、多元统计分析方法概述

（一）多元统计分析应用价值

随着科学发展和时代进步。企业经营成本管理要求和预算需要都在日益提升。统计学在应用数学知识的基础上，逐渐与计算机技术相融合，利用计算机快速、有效的应用能力。多元统计学作为经典统计学的一个重要分支，遵循了继承、发展的原则。通过多元统计分析方法的运用，为企业的经济指标进行科学合理的建模和预测。

运用多元统计分析方法，能更有效的解决当前企业工资总额管控的预算桎梏，以成熟的统计学理论有效实现工资总额的多元化预测以及应用建模。

（二）方法综述

1. 多元统计分析主要方法

基于统计分析的经济案例中，广泛应用的多元统计方法有以下几种：多元回归分析、因子分析法、主成分分析以及对某一变量的时间序列分析。该课题研究选取多元回归分析以及主成分回归来对企业的工资总额预算进行建模分析。

2. 多元線性回归模型

多元线性回归模型的为：

y^=β0+β1x1+β2x2+β3x3+β4x4+β5x5+βnxn+ε（1）

其中，β0为回归常数项， ε为随机误差（假设满足等方差、不相关假设，服从标准正态分布，σ2是未知参数，x1，x2，x3，x4，x5，…，xn为非随机变量，y为随机变量。

回归分析需要对模型中的未知参数β0，β1，β2，β3，β4，β5，…，βn及σ2做出估计，并且对建立的回归方程进行参数检验和设定检验，通过检验的模型可以用来解释现象和对未来进行预测。

对于模型的过程检验包括基本假设的满足性检验、选模型以及多重共线性检验。根据模型所存在的问题进行相应的处理，如果违背基本假设，需进行加权最小二乘估计;如果确定不了模型变量的选择，则进行选模型，通常采用逐步回归法进行选择;如果存在多重共线性，则需要消除多重共线性，通常采用主成分回归。与此同时，还可以对非线性回归进行建模比较所得的拟合值，以求得到更为优化的多元线性回归模型。

（1）回归模型检验分析与修正。建模目的是为了应用于经济问题，回归建模确定后，还需进一步对模型进行检验分析，验证被解释变量和解释变量之间的关系是否满足基本假设条件。对于回归模型的检验需要进行统计检验和模型经济意义检验。

（2） 统计检验。统计检验是整个回归模型确定的重要验证过程，包括对回归模型的相关显著性检验，回归系数的显著性检验，相关性的拟合优度检验，随机误差项的序列相关性检验，异方差性检验以及多重贡献性检验。对于不满足模型的统计检验的回归问题，则需要根据各类问题进行进一步的模型修正。

（3）模型经济意义检验。经济运用方面的回归模型中，有不少的模型通过了系列的统计检验，然而经济解释不甚合理，系数的正负号不符合经济意义。如果所见模型存在经济意义不合理的问题，则需要对模型进行不断的修正，以得到理想的回归模型投入应用。

二、工资总额案例分析

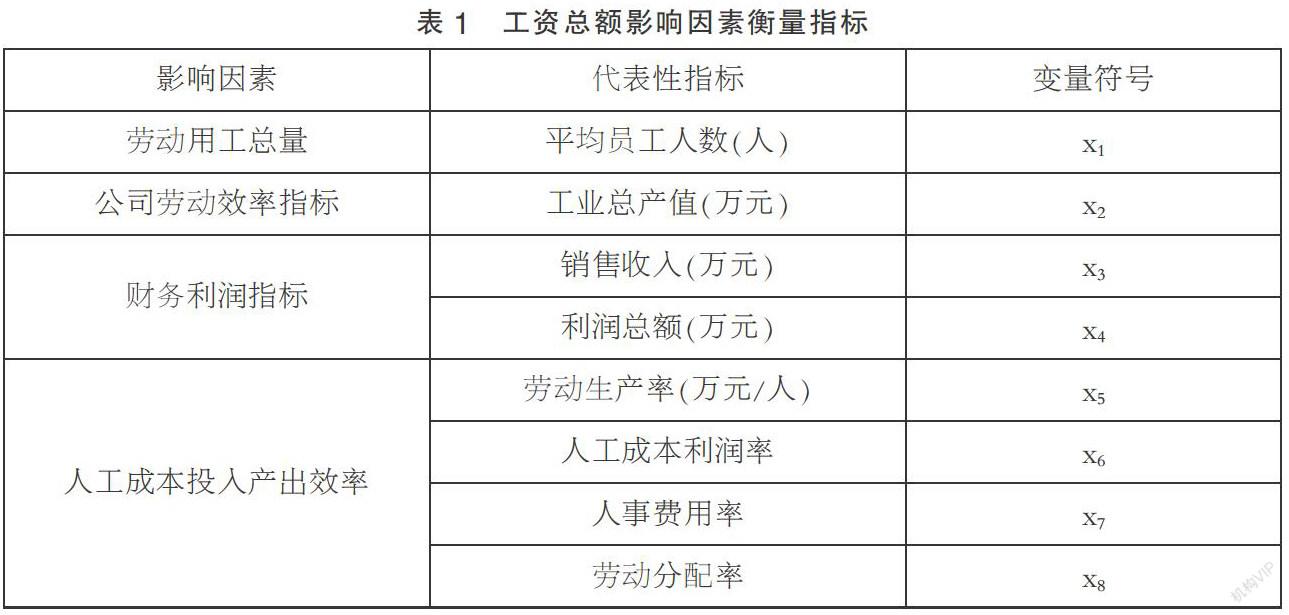
为提升公司工资总额管控水平，加强统计分析方法的应用实践，研究影响工资总额（万元）的因素，进行回归建模应用于当前公司实际工资总额管控预测，结合历史实际情况，选取了表1中的影响工资总额的主要因素。

（一）相关性分析

对原始数据进行标准化后，进行相关性分析，根据相关系数矩阵结果，得出利润总额与人工成本利润率，人工成本利润率与人事费用率，工业总产值与销售收入，存在着突出的相关性，符合实际经济运行情况中指标间的影响关联性。在统计分析建模过程中需要考虑回归模型存在多重相关性。

（二）多元线性回归初步建模

1.初步建模

首先对样本数据进行多元线性回归初步建模，使用SPSS软件得出线性回归输出结果，由回归系数表得到多元线性回归模型：

y^=-4704.69+1.46x1-0.01x2+0.06x3-0.45x4+402.92x5+2581.04x6+8686.71x7+218.08x8（2）

2. t检验分析

各自变量的回归系数都通过了t检验，t检验用于检验回归系数的显著性，输出结果表明各项指标的回归系数都通过了显著性检验。