基于事故属性及时空相关性的突发事件下交通量预测方法

何雅琴 陈俊

摘  要：为了提高突发事件下交通量预测的便捷性和预测精度，提出了一种基于事故属性及时空相关性的突发事件下交通量预测方法;引入事故属性维度，分析交通事故交通流变化的时空相关性，将当前突发事件与历史数据库中的突发事件进行相关度分析，利用灰色预测模型对突发事件下交通量进行预测;最后以上海市延安路高架的實测交通事故数据进行了案例分析。结果表明，与其他预测方法相比，该方法快速简单，且与实际数据对比，该预测方法的平均相对误差为3.014%，证明该方法是有效的。

关键词：交通量预测;突发事件;时空相关性;事故相关性;灰色预测

中图分类号：F570    文献标识码：A

Abstract： In order to improve the convenience and prediction accuracy of traffic volume prediction under emergencies， a traffic volume prediction method under emergencies based on accident attributes and time-space correlation is proposed; the dimensions of accident attributes are introduced to analyze the time and space of traffic flow changes in traffic accidents correlation： analyze the correlation between current emergencies and emergencies in the historical database， and use the gray prediction model to predict traffic volume under emergencies; finally， a case analysis is made with the measured traffic accident data of Shanghai Yan'an elevated highway. The results show that compared with other forecasting methods， this method is fast and simple， and compared with actual data， the average relative error of this forecasting method is 3.014%， which proves that this method is effective.

Key words： traffic volume prediction; emergencies; spatio

-temporal correlation; accident correlation; grey prediction

0  引  言

随着社会经济的发展及机动化进程的加快，城市突发事件发生愈来愈频繁，对道路上的交通正常运行带来一定的负面影响。对突发事件下的交通流进行预测有助于交通管理部门准确掌握城市道路交通流运行状态及变化[1]，从而采取及时有效的交通管制措施。

目前，国内外学者对城市道路交通流预测进行了大量的研究，也取得了丰富的成果，如Kumar Selvaraj Vasantha[2]提出了一种基于卡尔曼滤波技术（KFT）的交通流预测方法。Messai Nadhir[3]等提出了一种基于前馈的神经网络模型来预测短时交通流，并利用真实交通数据验证了该模型的预测性能。Zhang Qianqian[4]等分析了北京市某地区的交通流量特征，并建立了基于BP神经网络的交通流量预测模型。Deshpande Minal[5]等将神经网络和模糊逻辑的互补功能结合在一起，进行短时交通流量预测。Hou Qinzhong[6]等首先利用线性自回归综合移动平均（ARIMA）方法和非线性小波神经网络（WNN）方法来预测交通流量，然后通过模糊逻辑对两个模型的输出进行分析和组合，并将加权结果作为最终预测结果。文峰[7]等考虑了道路交通流量的时空特性，建立了基于支持向量回归（SVR）的交通流量预测模型，并使用实际交通流量数据来验证该模型的有效性。蔡翠翠[8]等通过对交通流时间和空间特性的分析，利用灰色神经网络组合模型对预测路段进行短时交通流预测，有效提高了预测精度。但是，国内外大部分学者都只是考虑了正常交通状态下的交通流预测，对于突发事件下的交通流预测研究相对较少。M Levin，G M Krause[9]利用上游和下游时间占有率之间的差异和上游空间占有率作为交通流特征，基于贝叶斯算法进行突发事件状态下的交通流预测。黄宝静[10]等基于事故路段上下游速度相关性，结合随机森林、ARIMA模型以及卡尔曼滤波算法对突发事件下的交通流进行预测。陈岳明[11]等利用异常突发事件下交通流序列特征，引入基于跳转的ARIMA模型，对突发事件下路段的交通流进行预测。文江辉[12]等考虑到突发事件下交通流中不同类型车辆的换道规律，提出了一种含概率崩塌各异性的改进沙漏模型来进行突发事件下的交通流预测。

目前已有的预测方法如支持向量机、卡尔曼滤波、神经网络等预测模型需要大量的历史训练数据，且计算过程繁琐，无法很好地满足突发事件下需要快速响应的要求。因此，本文引入事故属性维度，基于突发事件下交通流变化的时空特性，提取交通事故数据的判定属性数据（事故发生时间、事故占道情况、事故路段车道数、天气状况以及是否工作日等），并将当前交通事故和历史数据库中交通事故的判定属性数据进行对比，通过相关度计算从历史数据库中找到与当前交通事故相关性最强的事故的交通流序列，利用灰色预测模型来快速预测当前事故发生后的交通量，为交通管理部门及时有效管制交通提供技术支持。

1  突发事件下交通流时空相关性分析

交通流量既具有时间相关性，又具有空间相关性[13]。本文利用上海市延安高架2018.8.26～2018.9.8采集到的交通事故数据和交通量数据，提取并分析交通事故数据的判定属性数据，对突发事件下交通流的时空相关性进行具体分析。

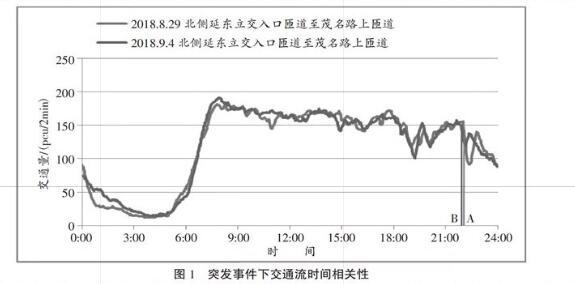
1.1  时间相关性分析。时间相关性主要是指交通流在不同时间下的规律相似性。为了更好地分析突发事件下交通流的时间相关性，并使不同事故的交通流在不同时间下的规律相似性更加明显，在交通事故数据集中，选取事故属性相似，事故空间位置相近，时间不同的两起事故进行分析，这两起事故分别是2018年8月29日22：02和2018年9月4日22：00发生在北侧延东立交入口匝道至茂名路上匝道之间路段上的交通事故，事故均占据一车道，事故当天均为工作日且均为多云天气，如图1所示，其中A、B代表事故发生的时刻。从图中可以看出，两条曲线整体的变化趋势具有明显的相似性，且在A点和B点之后的变化趋势也具有一定的相似性，说明突发事件状态下的交通流量变化在时间上存在一定的相关性，即突发事件下的交通流具有时间相关性。

1.2  空间相关性分析。空间相关性主要是指交通流在不同空间位置下的规律相似性。同样地，为了更好地分析突发事件下交通流的空间相关性，并使不同事故的交通流在不同空间位置下的规律相似性更加明显，在交通事故数据集中，选取事故发生时间相近，空间位置不同的两起事故进行分析，这两起事故分别是2018年9月7日13：18在北侧延西立交入口匝道2至娄山关下匝道之间路段发生和2018年9月7日13：04在南侧江苏路上匝道至华山路上匝道之间路段发生，事故均占据一车道，事故路段均为3车道。两起事故的交通量在事故发生前后的变化曲线如图2所示，其中C、D分别表示两起事故发生的时刻。从图中可以看出，两条曲线整体的变化趋势具有明显的相似性，且在C点和D点之后的变化趋势也具有一定的相似性，说明突发事件状态下的交通流量变化在空间上存在一定的相关性，即突发事件下的交通流具有空间相关性。

2  事故相关性分析

2.1  事故属性聚类分析。为了简化计算以及提高预测模型的精度和效率，本文先将历史数据集中的事故样本通过事故属性进行聚类分析，主要从事故路段车道数、事故发生时间、事故类型、事故占道情况、天气状况以及是否工作日等几个方面进行聚类分析。具体的事故属性聚类步骤如下。

Step1  将获取得到的交通事故构建历史交通事故数据集，并提取事故判定属性数据;

Step2  在历史交通事故数据集中筛选出与某一事故a事故路段车道数相同的事故，将其记作集合M;

Step3  在集合M中筛选出与事故a事故发生时间相近的事故，将其记作集合N;

Step4  在集合N中筛选出与事故a事故类型一致的事故，将其记作集合O;

Step5  在集合O中筛选出与事故a事故占道情况相同的事故，将其记作集合P;

Step6  在集合P中筛选出与事故a事发当日天气状况相似的事故，将其记作集合Q;

Step7  在集合Q中筛选出与事故a事发当日工作日类别一致的事故，将其记作集合R，集合R即为与事故a相似的样本事故集。

2.2  事故相关度计算。通过事故属性聚类分析找到某一事故a相似的样本事故集R之后，为了找出样本事故集R中与事故a相关程度最高的一起事故，引入相关系数概念，计算相似事故交通流序列的相关度，利用的是事故发生前10min的交通流量数据，最后将得到的相关系数最大的样本事故m作为与事故a事故相关度最强的事故。

相关系数是由统计学家卡尔·皮尔逊最先提出的统计指标，是研究两个变量之间线性相关程度的量[14]，一般用字母 r 表示，计算公式如式（1）所示。

r=                                        （1）

其中：r為两个交通流序列的相关系数，x、y表示两个交通流序列。0≤r≤1，r越大，说明x和y的相关程度越强。r越小，说明x和y的相关程度越弱。

3  灰色预测模型

灰色预测模型具有建模所需样本量少、计算量小等特点。基于此，本文利用灰色预测模型来进行突发事件下的交通量预测。通过对当前事故和相关事故的相关度计算，得到强相关事故，对当前事故和强相关事故的历史交通流序列进行灰色模型GM1，1建模。灰色预测模型GM1，1用较少的数据序列对系统进行定量分析，主要过程是将原始序列经过累加后生成新的数据序列，建立微分方程，通过对微分方程求解得出系统模型[15]。建模步骤如下：

第一步，数据的预处理，求出原始交通流量数据列的数列级比，λk为数列级比：

λk=                                            （2）

所的级比均需在可容覆盖区间X=e， e内，则数列x才可以建立GM1，1模型以及进行灰色预测。否则，对数据做适当的变换处理。

第二步，建立GM1，1灰色预测模型xk+αxt=b，用回归分析法算出α，b，其中xk为原始数据，xk为生成数据。算出α，b后，得出白化模型方程：

+αxt=b                                           （3）

从而相应得到预测值k+1=k+1-k， k=1，2，3，…，n-1。

第三步，对预测值进行检验处理：计算出原始数据和预测值的相对残差值εk：

εk=， k=1，2，…，n                                       （4）

如果对所有的εk<0.1，则认为到达较高的要求;若对所有的εk<0.2，则认为达到一般要求。

4  案例分析

4.1  数据来源。仍然采用上海市延安高架2018.8.26～2018.9.8采集到的95起交通事故数据和交通量数据作为数据样本进行分析。交通量数据的采样间隔为2min。构建预测模型时，在数据集中随机选取一起事故A（2018年9月5日13：26发生在南侧江苏路至华山路上匝道之间路段上的一起事故），假设事故A为当前发生事故。

4.2  事故相关性分析

（1）事故属性聚类分析。通过事故属性聚类筛选得到与事故A相似的样本事故集R，其中包含5组样本事故，结果如表1所示。

（2）事故相关度计算。在事故属性聚类筛选结果的基础上，根据相关系数计算公式（式1），利用事故发生前10min的交通流量数据，分别计算样本事故集R中5起事故与事故A的相关度，结果如表2所示。

计算所得到的相关系数均大于0.5（依据数学理论上的划分，当r>0.5时，说明这两个时间序列相关程度显著），如图3所示，其中，事故3与事故A的相关系数最大，对应的相关系数为r=0.97，说明事故3与事故A强相关。于是确定事故3（2018年9月4日13：22发生在北侧虹许路上匝道至外环机场出口匝道之间路段的一起事故）为与事故A最相似的样本事故。

4.3  灰色预测。通过事故属性聚类分析以及事故相关度计算找到与当前事故A最相似的样本事故3之后，对事故3进行快速整理分析，找出事故3在事故持续时间范围内的交通流量数据（记为数据B）：B=q，q，…，q=（145，136，129，122， 115，109，103，98，92，99，109，114，120，126，133，140，147），然后将数据B输入灰色预测模型，对事故A发生之后道路的交通流量数据进行预测。

第一步：建立數据B即为原始交通流量数据x，时间间隔为2min。

将x=q，q，q，…，q=145，136，130，121，116，107，102，98，94，99，107，113，122，128，135，140，145进行预处理，求出原始交通流量数据列的数列级比：

λ=1.066，1.046，1.074，1.043，1.084，1.049，1.041，1.043，0.949，0.925，0.947，0.926，0.953，0.948，0.964，0.966得到的级比均在可容覆盖区间0.889，1.125内，因此x可以建立GM1，1模型和灰色预测。

第二步：建立GM1，1灰色预测模型，得出白化模型方程并相应得到预测值。

为了减小随机序列的随机性和波动性，将x累加得到新的数列，然后建立关于白化形式的微分方程：

+αxt=b

通过Matlab计算结果即为预测值：

=q，q，q，…，q=145，136，129，122，115，109，103，98，92，99，109，114，120，126，133，140，147

第三步，对预测值进行检验处理。

计算出原始数据和预测值的相对残差值，如表3所示，其中εk为相对残差值。

表3中所得到的相对残差值εk均小于0.1，如图4所示，认为达到比较高的要求标准。

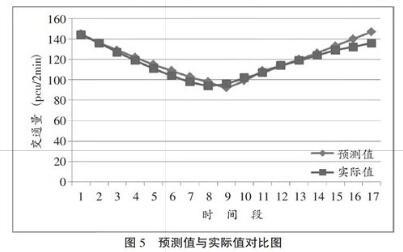
4.4  预测结果分析评价。通过灰色预测模型得到预测值之后，将预测值与实际值——即事故A发生之后的交通流序列（记为数据A）：A=q，q，…，q=144，136，127，119，111，104，98，94，96，102，107，114，119，124，129，132，136进行对比分析，结果如图5所示。从图5中可以看出，灰色预测模型的预测值与实际值之间的差值并不大。

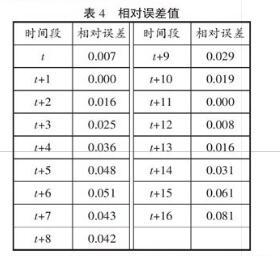
为了更加准确地评判灰色预测模型的预测性能，计算预测值与实际值之间的相对误差，如表4所示，预测值与实际值之间的相对误差均小于0.1，同时，计算出平均相对误差为3.014%，说明提出的灰色预测模型是有效的。

5  小  结

（1）本文引入事故属性维度，考虑突发事件下交通流变化的时空特性，计算事故之间的相关度，利用灰色预测构建模型进行突发事件下交通量预测，预测误差在允许范围内，且该预测算法较为简单，应用性较强。

（2）由于采集到的历史数据库中事故样本量较少，且事故聚类分析时采用了Excel的筛选功能，使得数据筛选太严格，得到聚类之后的事故样本太少，可能会使案例中的预测结果存在一定的误差，但是在车联网和交通大数据的时代背景之下，今后交通事故数据及交通量数据的收集会变得更加容易，另外下一步会对事故聚类分析方法进行深入研究，因此，该方法的预测精度将会进一步提高。

参考文献：

[1] 贺新光. 基于突变理论的城市路网交通状态判别与预警研究[D]. 重庆：重庆交通大学（硕士学位论文），2016.

[2]  Kumar S V. Traffic Flow Prediction using Kalman Filtering Technique[J]. Procedia Engineering， 2017，187（1）：582-587.

[3]  Messai N， Thomas P， Lefebvre D. A neural network approach for freeway traffic flow prediction[J]. IEEE Conference on Control Applications-Proceedings， 2002，2（1）：984-989.

[4]  Zhang Q， Liu S. Urban traffic flow prediction model based on BP artificial neural network in Beijing area[J]. Journal of Discrete Mathematical Sciences and Cryptography， 2018，21（4）：849-858.

[5]  Deshpande M， Bajaj P R. Short term traffic flow prediction based on neuro-fuzzy hybrid sytem[J]. Proceedings of 2016 International Conference on ICT in Business， Industry， and Government， ICTBIG 2016， 2017（1）：2020.

[6]  Hou Q， Leng J， Ma G. An adaptive hybrid model for short-term urban traffic flow prediction[J]. Physica A： Statistical Mechanics and its Applications， 2019，527：121065.

[7] 文峰，張国. 基于SVR的短时交通流量预测[J]. 科技创新导报，2018，15（25）：189-190.

[8] 蔡翠翠，王本有，常志强. 基于时空特性和灰色神经网络的短时交通流预测[J]. 沈阳理工大学学报，2019，38（2）：32-36，43.

[9] Levin M， Krause G M. Incident detection： a Bayesian approach[J]. Pubtisher SAGE Pubtishing， 1978，682：52-58.

[10] 黄宝静. 突发事件下道路交通流预测方法研究[D]. 北京：北京交通大学（硕士学位论文），2016.

[11] 陈岳明，杨帆. 异常突发事件下交通流特征分析与预测[J]. 科学技术与工程，2016，16（23）：75-78.

[12] 文江辉，江泽武，徐佳恒，等. 基于改进沙漏模型的突发事件下交通流预测[J]. 交通运输系统工程与信息，2014，14（6）：86-91.

[13] 熊亭，戚湧，张伟斌，等. 基于时空相关性的短时交通流预测模型[J]. 计算机工程与设计，2019，40（2）：501-507.

[14] 熊娟，吴萌. 城市道路的交通事件影响范围预测方法研究[C] // 2014第九届中国智能交通年会大会论文集. 北京：中国智能交通协会，2014.

[15] 于涛，黄涛，潘膺希，等. 基于BP神经网络和灰色关联度组合模型的城市生活垃圾清运量预测[J]. 安全与环境学报，2013，13（4）：94-97.