突发事件下考虑外协和弹性的 制造商库存策略研究
陈俐 方叶祥 甘平


摘 要:由于突发事件的不确定性,制造商往往会面临缺货的风险,为了减少缺货损失和提高服务水平,制造商采取外協策略以应对紧急缺货。从制造商的年需求满足度出发,在同类企业相互协作的背景下构建制造商库存决策的成本
—弹性模型,研究制造商最优库存决策。采用精英策略的非支配排序的Nsga-Ⅱ遗传算法和数值仿真得出制造商外协策略成本—弹性模型的最优库存决策,并对模型中的参数进行了分析。研究结果表明,为保证总成本最小,当信息误差率较低时,应适当减少初始期初库存,为降低信息共享误差率,可建立信息共享平台,使供需双方信息透明化;当需求越不稳定时,更需要加强制造商间的协作,建立长期合作框架协议,以便共同抵御突发事件的影响。
关键词:突发事件;外协;需求满足度;弹性
中图分类号:F253 文献标识码:A
Abstract: Due to the uncertainty of emergencies, manufacturers often face the risk of stock shortage. In order to reduce the loss of stock shortage and improve the service level, manufacturers adopt outsourcing strategies to deal with emergency stock shortage. Based on the annual demand satisfaction of the manufacturer, the cost-elasticity model of the inventory decision of the manufacturer is constructed under the background of the cooperation of similar enterprises, and the optimal inventory decision of the manufacturer is studied. The elite strategy of non-dominated sorting the Nsga-Ⅱ genetic algorithm and numerical simulation that manufacturers outsourcing strategy cost-elastic model of optimal inventory decisions, and analyses the parameters in the model. The results show that,in order to minimize the total cost, when the error rate of information is low, the initial inventory should be appropriately reduced. In order to reduce the error rate of information sharing, an information sharing platform can be established to make the information of the supply and demand parties transparent. When the demand is more unstable, it is more necessary to strengthen the cooperation between manufacturers and establish a long-term cooperation framework agreement, so as to jointly resist the arrival of emergencies.
Key words: emergency; outsourcing; degree of demand satisfaction; elasticity
0 引 言
近年来,随着突发事件的频繁发生,企业面临着巨大的考验。突发事件会直接导致供应的中断,并且由于突发事件的持续性影响,如果没有及时应对,那么将会给企业带来巨大的经济损失。因此,突发事件下企业的管理策略越来越受关注。关于预防和应对突发事件的库存管理策略,学者们有所研究:Beamon等[1]从人道主义角度出发,建立随机库存控制模型,研究了长期紧急救援反应的最优订货数量和再订货点;Selda等[2]提出了一种基于飓风预测模型的多周期库存决策;Taskin等[3]提出了一种具有飓风预报更新的贝叶斯决策模型;王芹等[4]运用最优性原理分析了突发事件影响下的最优订货批量、最佳订货周期和最大利润的存在性问题。以上研究企业发生紧急情况时采取的是独立响应策略,而独立响应策略往往采取的措施有:设置更高的安全库存,选择多个供应商,降低设备利用率等,采取增加冗余资源来独立响应突发事件,一方面企业会面临高成本问题,另一方面,对于严重的突发事件,单独的企业无法获得足够的资源来应对。由于企业对于突发事件的独立响应是存在缺陷的,所以突发事件下企业间的协同应对机制成了学者们的热点关注话题[5-9]。
在企业协同应对突发事件的研究中,不少学者认为企业的协同合作增强了企业的弹性,但是都没有明确给出弹性的定义和定量化描述。关于弹性的定义问题,早在1973年,Holling[10]就提出弹性是系统平衡被打破前吸收扰动的能力;Brandon等[11]定义弹性为受到干扰的可接受的时间内恢复正常的能力;孟宏旭[12]将弹性定义为系统在受到干扰时, 快速恢复到最初状态或一个更好状态的能力;蔡振英[13]定义弹性为面对内部或外部干扰时,能够自我恢复的一种性能。关于弹性的定量化描述,Anupam等[14]提出了一种基于模糊技术的订单偏好综合模糊决策方法,用容量缓冲投资、反应能力和应对危机持有战略库存的能力三个指标来衡量弹性;王宇奇等[15]研究了我国原油供应链的适度弹性,将时间指标和成本指标相结合构建弹性系数;Petti等[16]提出了一个帮助企业应对变化的新的弹性框架,从脆弱性和能力两方面衡量弹性。通过以上研究发现,到目前为止,仍没有明确的弹性定义,对于弹性的定量化描述也是各有千秋。本文将弹性定义为企业发生中断后的及时响应能力。特别借鉴刘飞[17]模型中对于弹性的定量化表述,采用发生紧急缺货前后的需求满足度来衡量其弹性。
外协是将资源延伸的一种方式,其主要指由于本企业生产能力不足或有特殊工艺要求,由其它单位或组织协作完成任务。在同类产品制造业的环境下,针对制造商A遭遇突发事件,生产能力已达最大化且发生了紧急缺货的情况,采取外协策略以及时应对突发状况。本文中的外协策略是指在制造商A发生紧急缺货时,区域内有制造商B以高出产品单价的价格提供产品转运服务(文中以A表示外协需求方,B表示产品转运供应方)。本文研究的是突发事件下的紧急缺货情况,在实行外协策略后制造商A能以最小的年总成本获得最大的需求满足比,并得出库存最优决策。需求预测的准确性是库存决策中的重要决定因素,制造商根据零售商分享的需求信息做决策,但分享的信息并不是零售商的最优决策[18]。很有可能存在零售商为了私有的利益而谎报需求信息的情况[19],从而影响了需求预测的准确性,进而导致制造商做出的库存决策并不合理。本文为了得到更合理的库存决策在模型中加入了信息共享误差率因素。
1 问题描述及库存协同模型构建
1.1 弹性的定义
本文定义弹性为制造商A发生缺货(生产能力已达最大化)能立即响应的能力。以紧急补充库存后制造商A的需求满足度与发生缺货时制造商A的需求满足度的比值来衡量弹性,其中,需求满足度表示为年生产能力与年实际需求的比值,表达式如下:
ε= (1)
其中:ε表示彈性,i表示季度,X表示制造商A的实际需求量;S表示制造商A的生产能力,本文制造商A的生产能力以其当期计划产量S表示,计划产量S=需求预测量+安全库存量S-期初库存量S,即S=+S-S,由于需求预测的不确定性高,所以会设定一定量的安全库存S=α*λ*(λ表示信息共享误差率,λ越高,意味着信息共享越不准确,在0~1之间取值)。
1.2 问题描述
以包含多个同产业制造商的区域为研究背景,区域内各个制造商生产着可完全相互替代的同一种产品。当某一制造商在面临突发事件导致的紧急缺货且生产能力已达最大化时,需要区域内另一制造商提供紧急补货,A表示外协需求方,B表示产品转运可供方,外协策略合作如图1所示。
本文假设区域内各个制造商面临的需求满足相同且独立的正态分布:N=μ,σi=1,2,3,…。各个制造商面临相似的市场需求,因此会出现以下几种可能:(1)制造商面对下游分销商过高的订货发生缺货;(2)制造商面对下游分销商的订货减少发生库存积压的情况;(3)制造商跟分销商的供需相等。本文考虑的是第一、二种可能情况。当制造商A发生缺货且生产能力已达最大化时,需要找制造商B实行外协策略。
1.3 基本假设
(1)区域内的制造商面临的市场需求遵循相同且独立的概率分布;
(2)当发生缺货时,制造商的生产能力已达最大化;
(3)制造商A采取外协策略时,一定存在制造商B可以成功补货;
(4)产品需求和生产能力为整数。
1.4 构建模型目标函数
制造商A的成本主要由以下两部分构成:(1)短缺成本:发生缺货时的惩罚成本和产品订购成本;(2)存储成本:产成品库存可以满足下游需求,剩余的产成品库存用作下期期初库存的存储费用。本文计算的是制造商A的年度总成本,分季度计算。
当制造商A的本季度的产品需求大于其生产能力时,需要进行产品订购。已知产品需求的密度函数为fx, 分布函数为FX=PX>S=fxdXi=1,…,n。单位产品生产成本为C,单位产品订购成本为C,单位产品缺货惩罚成本为C,则A的第i季度的短缺成本为:
C=C+C·X-S·p·fXdX+C·S (2)
当制造商A的本季度产品需求小于等于最大生产能力时,库存可以满足需要。不考虑已使用产品的存储费用,已知单位产品存储成本为C,则第i季度A的存储成本为:
C=C·S-X·p·fXdX+C·S (3)
则,制造商A的年度总成本为:
EC=C+C·X-S·p·fXdX+C·S-X·p·fXdX+C·S n=4 (4)
下个季度的期初库存由上个季度的生产能力减去上个季度的实际需求得出,即:
S=S-X (5)
其中,第一季度的生产能力:
S=+α·λ·-S (6)
第二季度的生产能力:
S=+α·λ·-S-X (7)
第三季度的生产能力:
S=+α·λ·-S-X (8)
第四季度的生产能力:
S=+α·λ·-S-X (9)
本文的数学模型如下:
(10)
2 带精英策略的非支配排序的遗传算法Nsga-Ⅱ
2.1 Nsga-Ⅱ算法简介
NSGA-Ⅱ算法是Srinivas和Deb于2000年在NSGA[1]的基础上提出的,它比NSGA算法更加优越:它采用了快速非支配排序算法,计算复杂度比NSGA大大的降低;采用了拥挤度和拥挤度比较算子,代替了需要指定的共享半径ShareQ,并在快速排序后的同级比较中作为胜出标准,使准Pareto域中的个体能扩展到整个Pareto域,并均匀分布,保持了种群的多样性;引入了精英策略,扩大了采样空间,防止最佳个体的丢失,提高了算法的运算速度和鲁棒性。
2.2 算法计算过程
本文采用带精英策略的非支配排序的遗传算法Nsga-Ⅱ来求解该问题。
步骤1:随机产生规模为N的初始种群,非支配排序后通过遗传算法的选择、交叉、变异三个基本操作得到第一代子代种群;
步骤2:从第二代开始,将父代种群与子代种群合并,进行快速非支配排序,同时对每个非支配层中的个体进行拥挤度计算,根据非支配關系以及个体的拥挤度选取合适的个体组成新的父代种群;
步骤3:通过遗传算法的基本操作持续产生新的子代种群,直至满足结束条件。
求解过程见图2。
3 实证分析
3.1 基本仿真与分析
制造商A的某产品需求量随季度不同而变化且需求量大小服从正态分布N300,100^2,现下游零售商给出了后一年内四个季度该产品的需求预测,如表1所示。其他数据如下:单位产品生产成本为200元/件,单位产品存储成本为100元/件,单位产品订购成本为400元/件,单位产品缺货惩罚成本为1 000元/件。由于需求预测的不确定性高,另考虑有25%的安全库存。另外,下游给的需求预测值的信息共享误差率是1,计算结果如图3、图4所示。
图3左边可以看出,随着年实际需求量与年生产能力差值的减小,年总成本是逐渐增加的。在现实制造业的生产活动中,要实现需求与生产能力的平衡是很复杂且需要花费一定成本的,制造商A需要制定合适的综合生产平衡计划,如科学地确定产品的产量、根据企业的特点合理安排产品生产进度以及涉及到多品种时有效搭配生产等。
图3右边可以看出,制造商A的弹性是随着成本的提升先减小至零而后增加的。在发生紧急缺货后,制造商A需要动用全部的安全库存和采取外协策略后紧急补充库存来应对,随着可用库存的慢慢减少,制造商A的弹性逐渐减少至没有弹性;在紧急补充库存后,制造商A慢慢恢复产能,弹性也慢慢增加。
由图4可以看出,当需求预测出现季度性差异时,实际需求仿真出来也是跟需求预测一样的变化幅度,除了第一季二者比较接近外,后面三个季度实际仿真值都大于需求预测值,且第二季度后,制造商A的生产能力一直下滑,这意味着制造商A在下一年的生产计划要更改,尤其是第二季度,可以增加安全库存量,提高计划产量。
3.2 变动参数仿真与分析
由成本—弹性模型可以看出,需求量的不稳定程度和信息共享误差率是成本和弹性的影响因素,因此有必要对这两个因素进行进一步分析。
(1)信息共享误差率λ的影响分析
由于制造商A的生产计划是根据下游零售商给的需求预测值所决定的,需求预测的可靠性对制造商A的生产决策意义重大。需求预测的可靠性由信息共享误差率λ表示,λ的范围是(0,1],λ越接近1,表示下游给的需求预测越不可靠,λ越接近0,则意味着下游给的需求预测越可靠。
由图5可以看出,信息共享误差率λ与总成本呈正相关。随着信息共享误差率λ的增加,成本也是增加的。这说明,需求预测的信息共享误差率对成本影响很大,怎样减小信息共享误差率对制造商有效控制成本来说意义重大。制造商A可以通过支付信息共享费用来激励零售商共享需求预测信息[20],也可以在产品具有互补性时,制造商A通过设定一定的收益共享契约,在分享零售商一部分收入前提下,可降低批发价格,激励零售商进行信息共享[21]。
由图6可以看出,随着信息共享误差率的降低,初始期初库存也减少。这意味着当零售商给的需求预测越可靠时,可以适当降低初始期初库存量。
(2)需求量不稳定程度的影响分析
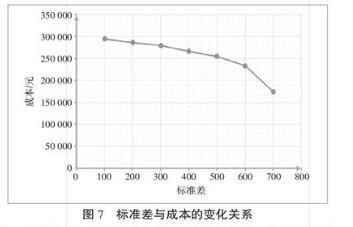
假设制造商A的某产品的需求服从正态分布N300,100^,通过标准差来表示制造商A面临的需求不确定程度。标准差越高,则需求不确定程度越高,意味着需求越不稳定,标准差越低则意味着需求越稳定。
由图7可以看出,当标准差增大时,成本逐渐减少。这意味着,当制造商A面临的需求不稳定程度越高时,越是应该采取外协策略,有利于控制总成本。
4 结论与展望
外协策略是企业在面对突发事件影响时可考虑采取的,尤其是面对较大的突发事件。本文通过研究同类产品制造业相互协作的背景下发生突发事件时制造商的库存决策,建立了考虑外协和弹性的制造商成本—弹性模型,求解考虑最大需求满足比最优期初库存与总成本。最后通过算例和参数变动分析,得出需求不稳定时,外协策略有利于制造商降低总成本,以及信息共享误差率越小,初始期初库存越小的结论。
本文在区域内有单一制造商B可以完成对制造商A紧急补货的假设下进行研究,后续研究可对多个制造商B对制造商A进行紧急补货进行研究。
参考文献:
[1] Beamon B, Stephen K. Inventory modelling for complex emergencies in humanitarian relief operations[J]. International Journal of Logistics Research and Applications, 2006,9(1):1-18.
[2] Selda T, Lodree EJ. Inventory decisions for emergency supplies based on hurricane count predictions[J]. International Journal of Production Economics, 2009,126(1):66-75.
[3] Taskin S, Lodree EJ. A Bayesian decision model with hurricane forecast updates for emergency supplies
inventory management[J]. Journal of the Operational Research Society, 2011,62(6):1098-1108.
[4] 王芹,高志军,徐最,等. 突发事件影响下应急物资的库存管理策略[J]. 上海海事大学学报,2018,39(1):80-84.
[5] 张宁,刘春林,王全胜. 企业间应急协作:应对突发事件的机制研究[J]. 商业经济与管理,2009(9):30-35.
[6] 王兴鹏,吕淑然. 基于知识协同的跨区域突发事件应急协作体系研究[J]. 科技管理研究,2016,36(8):216-221.
[7] Kapucu N, Arslan T, Demiroz F. Collaborative emergency management and national emergency management network[J]. Disaster Prevention and Management, 2010,19(4):452-468.
[8] Goran D Putnik, Varela L, Modr?觃k V. Intelligent Collaborative Decision-Making Models, Methods, and Tools[EB/OL]. (2018)[2021-01-31]. https://doi.org/10.1155/2018/9627917.
[9] 张海涛,刘雅姝,周红磊,等. 情报智慧赋能:重大突发事件的智能协同决策[J]. 情报科学,2020,38(9):3-8.
[10] Holling C. Resilience and stability of ecological systems[J]. Annual Review of Ecology and Systematics, 1973(4):1-23.
[11] Brandon J, Emma, Brian S, et al. A contingent resource-based perspective of supply chain resilience and robustness[J]. Journal of Supply Chain Management, 2014(50):55-73.
[12] 孟宏旭. 基于中断—应急的弹性供应链网络设计[J]. 物流技术,2018,37(12):110-114.
[13] 蔡政英,肖人彬. 中断环境下供應链弹性运作分析与优化[J]. 系统工程理论与实践,2014,34(6):1443-1452.
[14] Anupam H, Amitava R, Debamalya B, et al. Resilient supplier selection under a fuzzy environment[J]. International Journal of Management Science and Engineering Management, 2014,9(2):147-156.
[15] 王宇奇,刘金玲. 适度弹性视阈下我国原油供应链系统结构优化模型[J]. 系统工程,2018,36(11):127-139.
[16] Petti T, Fiksel J, Croxton K. Ensuring Supply Chain Resilience: Development of a Conceptual Framework[J]. Journal of Business Logistics, 2011,31(1):1-21.
[17] 刘飞. 突发事件下资源调度的医疗供应链网络弹性研究[D]. 南京:东南大学(硕士学位论文),2015.
[18] 翟昕,刘忠轶,吴江华. 基于零售商私有信息的分销系统协调[J]. 系统工程理论与实践,2011,31(10):1903-1911.
[19] Ruomeng C, Gad A, Achal B, et al. Information Sharing in Supply Chains: An Empirical and Theoretical Valuation[J]. Management Science, 2015,61(11):2803-2824.
[20] 王文隆,王成军. 基于竞争型制造商创新投入的零售商需求预测信息共享研究[J]. 中国管理科学,2020,28(8):127-138.
[21] 周建亨,王晓敏. 收益共享机制下的供应链纵向信息共享策略[J]. 系统管理学报,2018,27(5):971-980.

