基于逻辑回归的股指期货价格预测

顾书豪 罗效禹 何江 西华大学经济学院

一、引言与文献综述

中国的第一份股指期货合约沪深300股指期货合约于2010年4月16日推出。在这之后，随着金融市场的不断完善，相继推出了两种股指期货，包括上证50股指期货和中证500股指期货。由于股指期货市场流动性差，市场主体无法对冲风险。基于此，国内学者围绕股指期货展开了大量研究，尽管少数学者研究证实推广股指期货会降低股市波动的影响，但仍对能否稳定股市功能存在学术争议。现有对股指期货的研究多集中于期货的价格发现功能和波动溢出效应，使用的方法也是基于传统的计量模型。随着互联网时代的不断发展，更多的学者开始将机器学习、人工智能引入金融领域，这在股票市场、汇率市场开始出现，但对于股指期货市场的价格走势预测还相对较少。

事实上，现在有大量的国内外学者开始在金融领域通过在传统计量模型的基础上，加入机器学习进行研究，为资本市场的价格走势预测提供新的方向。Galeshchuk（2016）的研究通过描述和实证检验外汇市场数据发现了人工神经网络的经济目的。对汇率的面板数据（USD/EUR，JPY/USD，USD/GBP）进行了检验，并利用神经网络对时间序列进行了优化预测。Hew（2020）等人应用人工神经网络（ANN）来研究驱动移动社交商务的阻力。Lahmiri等人在金融数据分类中使用了集成学习。Lei（2020）等人提出了一种时间驱动的特征感知联合深度强化学习（DRL），用于金融信号表示和算法交易。Sermpinis（2013）等人引入了一种基于粒子群优化和自适应径向基函数（ARBFPSO）的混合神经网络结构和用于财务预测的神经网络适应度函数。这是通过标杆ARBF-PSO的结果与三种不同的神经网络架构（最近邻算法（k-NN），自回归移动平均模型（ARMA），移动平均收敛/辐散模型（MACD））的结果实现。Wang（2020）等人提出了一种由长短期记忆网络和均值-方差模型组成的混合方法，结合资产预选优化投资组合的形成，从而捕获金融时间序列数据的长期依赖性。该实验使用了1994年3月至2019年3月期间英国证券交易所100指数的大量样本数据。研究发现，长短时记忆网络适用于金融时间序列预测，比其他基准模型具有明显的优势。在国内，众多学者也开始将机器学习的方法运用到了金融领域之中。张瑞（2020）基于网络搜索数据，针对部分商品零售价格指数的非线性变化，采用支持向量机（SVR）对商品的零售价格指数进行预测。包振山等（2020）提出利用长短期记忆细胞神经网络（LSTM）预测中证500股票未来价格，并在此基础上，又运用遗传算法进行调参，进一步提高了预测效果。戴德宝等（2019）利用文本挖掘技术和情感分析方法生成情绪时间序列数据，用支持向量机和神经网络预测股票市场价格变化。杨康等（2017）提出利用基于细粒度演化超网络的股票预测方法，对证券年报数据进行处理，并预测其中的股票走势。

二、逻辑回归的理论介绍

预测股票的涨跌趋势本质上是一个二类分类问题。逻辑回归、费歇判别分析、支持向量机和人工神经网络等方法在价格走势预测中较为常见。由于支持向量机不能提供类概率估计，费歇判别分析需要对输入特征作正态分布假定，人工神经网络因为噪音累积、非平稳特征和复杂维数在学习方式上有限制等原因产生不稳定的预测精度，故本文采用既能提供类概率估计又能提高预测精度的逻辑回归模型作为二类分类函数。

（一）逻辑分布

逻辑分布是一种连续型的概率分布，其分布函数和密度函数分别为：

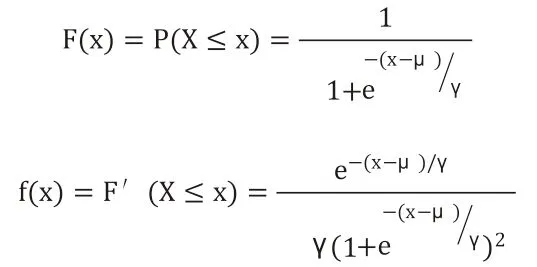
其中，μ表示位置参数，γ > 0为形状参数。

逻辑分布是由其位置和尺度参数定义的连续分布。逻辑分布的形状与正态分布的形状相似，但是逻辑分布的尾部更长，所以我们可以使用逻辑分布来建模比正态分布具有更长尾部和更高波峰的数据分布。

（二）逻辑回归

逻辑回归主要用于二分类问题，即对于所给数据集假设存在一条直线可以将数据完成线性可分，如图1所示。

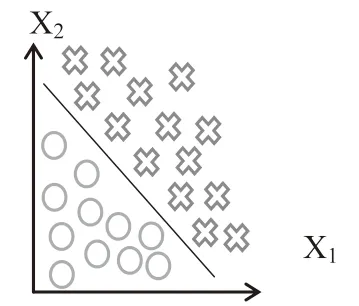
图1 数据集

决策边界表示为：w1x1+w2x2+b=0。假设某个样本点hw（x）=w1x1+w2x2+b>0，则可判断类别为1，逻辑回归在此基础之上，还要找到分类概率P（Y=1）与输入向量x的直接关系，通过比较概率值来判断类别。考虑到本文数据集所采用的二分类问题，给定数据集：

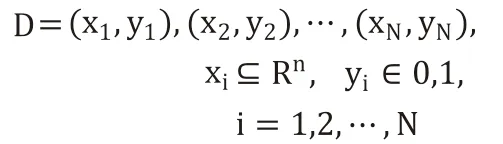
考虑到wTx+b取值是连续的，因此它不能拟合离散变量。可用它来拟合条件概率P（Y=1|x），因为概率的取值是连续的。但对于ω≠0，wTx+b取值为R，不符合概率取值从0到1，故采用广义线性模型。最理想的单位阶跃函数：

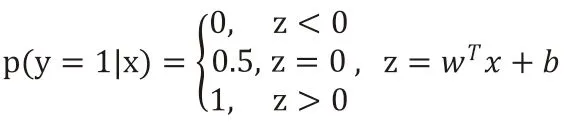
但这个阶跃函数不可微，取对数几率函数去替代该函数：

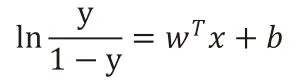
将y视为x为正例的概率，则1-y为x为其反例的概率。两者的比值称为几率，特指该事件发生概率与不发生概率的比值，若事件发生的概率为p。则对数几率：

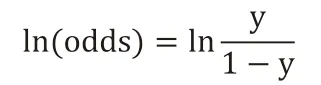
将y视为类后验概率估计，重新书写公式有：

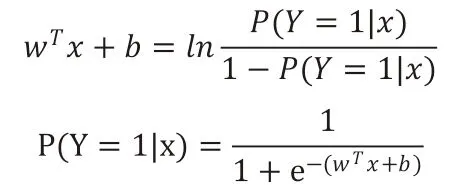
即对数几率输出为Y=1是由线性函数输入x表示的模型，这也就是逻辑回归模型。当wTx+b得的值越接近正无穷，P（Y=1|x）概率值也就越接近1。

（三）代价函数

在统计学中，经常使用极大似然估计法来求解，通过找到一组参数，在这组参数下，使得数据的似然度最大。设：

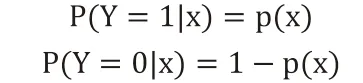
似然函数：

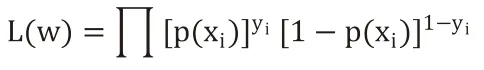
为了便于求解，在等式两边取对数，写做对数似然函数：

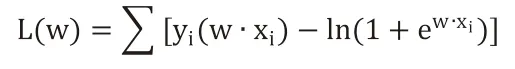
损失函数是衡量模型预测错误的程度。若取整个数据集上的平均对数似然损失，可得到：

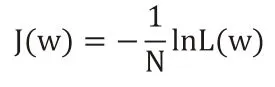
由此式可知，在逻辑回归模型中，最大化似然函数和最小化损失函数实际上是等价的。

（四）求解

求解逻辑回归模型的方法有很多种，本文采用了梯度下降算法。逻辑回归的损失函数是：

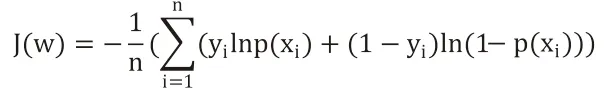
梯度下降算法通过J（w）对w的一阶导数来找下降方向，并以迭代的方式来更新参数，更新方式为：

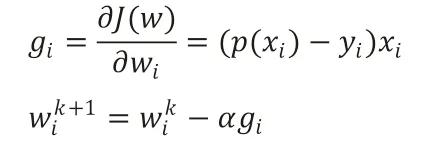
三、实证分析

（一）数据选取与处理

数据选用中证500股指期货从2015年4月16日9点14分到2016年12月30日14点59分的开盘价、最高价、最低价、收盘价、成交量的每分钟数据，共84328行有效数据。首先对数据进行简要分析，图2和图3为2015年4月16日9点14分 到2016年12月30日14点59分中证500股指期货的对数收益率极其波动率。

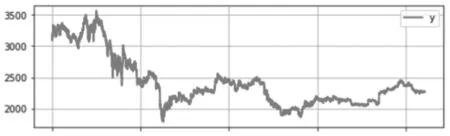
图2 对数收益率

从图3可以看出，中证500股指期货的对数收益率2015年到2016年12月间在1500-3500之间波动，且在2015年6月到8月价格水平波动较大，出现峰值之后开始下降；2015年9月至2016年12月在一个较低的价格水平内波动，没有明显的上升趋势。波动率主要波动幅度集中在（0.000，0.003）之间。将对数收益率与正态分布图相比中证500股指期货对数收益率呈现出尖峰后尾的特征，符合金融数据的波动特点（见图4）。

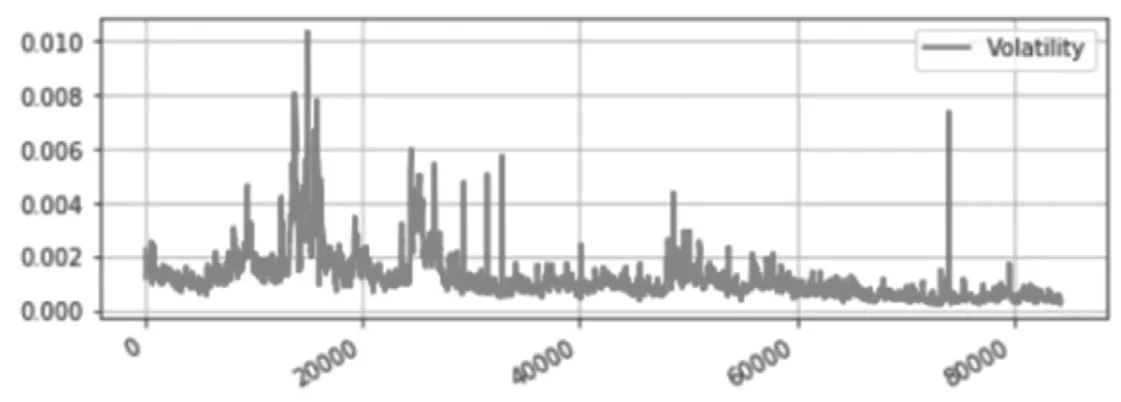
图3 对数收益率的波动率

图4 中证500股指期货对数收益率正态分布图

其次，将中证500股指期货指数前一天的最高价、开盘价、最低价、成交量作为逻辑回归的4个技术指标，将后一天股指期货收盘价的预测作为输出结果，将原始数据集按照8：2的比例随机分成训练集和测试集。表1是5个指标的描述统计量，从表1可知，5个指标标准差和均值均较大，且收盘价最大值为3564.6，最小值为1793，成交量每天最小成交1笔，最多成交8287笔，具体情况如表1。

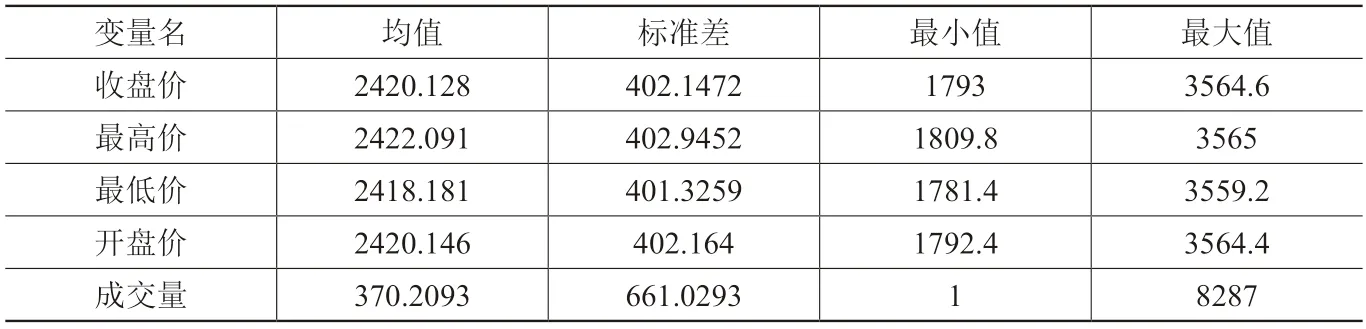
表1 5个技术指标的描述统计量

（二）逻辑回归模型预测股票涨跌

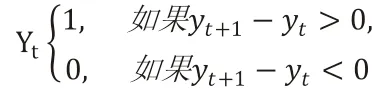
表示股指的涨跌趋势，则建模股指涨跌趋势的逻辑回归模型可以表示为：

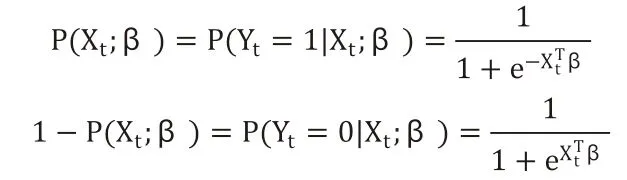
其中β=（β0，β1，…，β5）T

（三）原始数据预测

按照上文对逻辑回归模型的分析与建立，对中证500股指期货指数2015年4月16日9点14分到2016年12月30日14点59分的全部数据进行整体回归分析预测，得到的回归预测拟合结果如图5所示。从图中可以看出拟合值与真实值基本重合，表示拟合效果良好，得到的均方误差为1.430，部分预测值与真实值比较如表2所示。

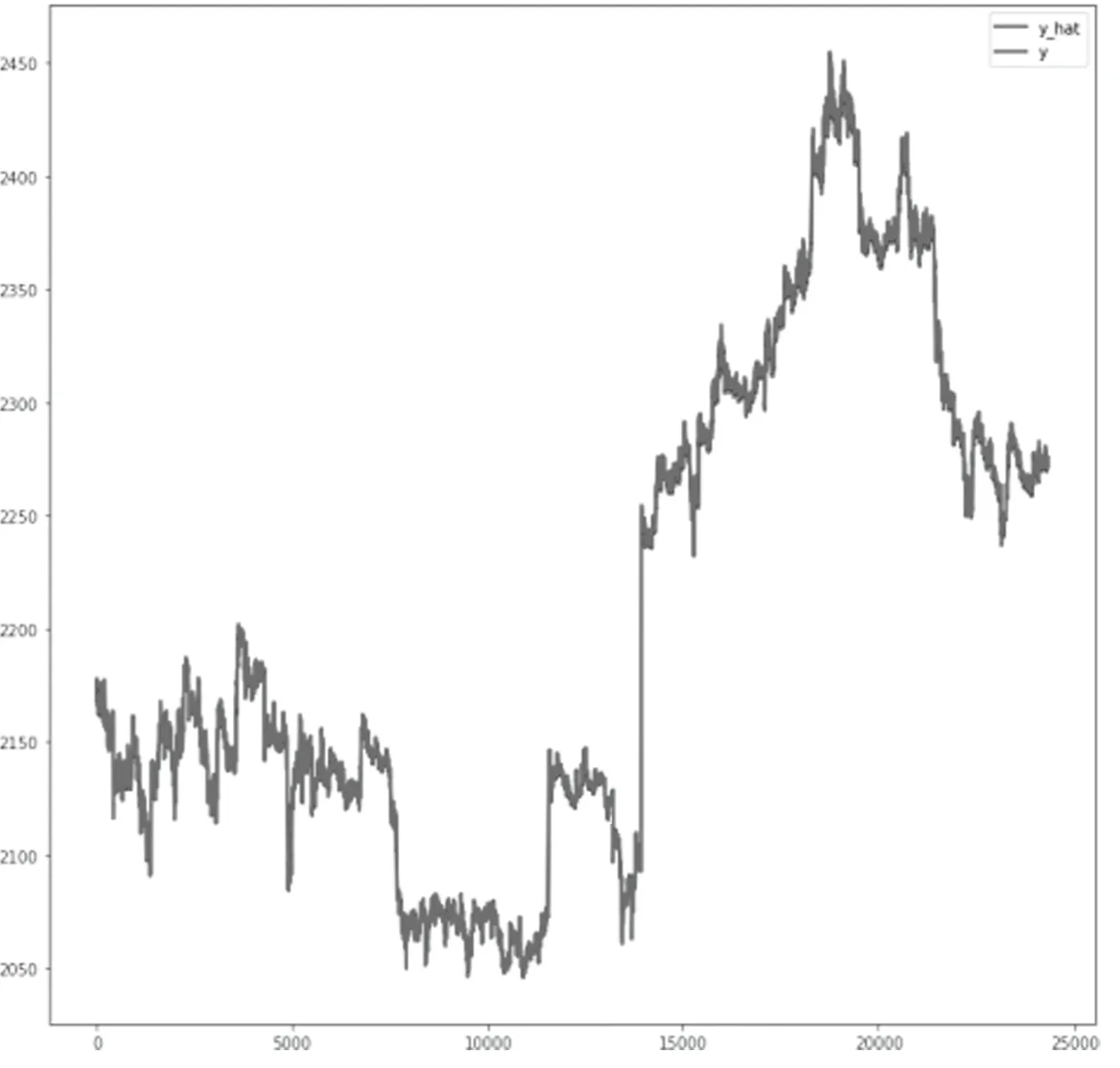
图5 整体回归拟合图

表2 部分预测值与真实值比较

四、结论

股指期货于2011年4月推出，相对于股票发展时间较短。针对于股指期货的研究也大多是对股指期货的市场波动进行研究，对于股指期货本身的预测问题相对较少，且多用计量统计的办法进行预测，但多是使用传统的线性经济学模型，不能应对非线性的股指期货市场。随着互联网时代的发展，人工智能、机器学习开始大范围应用于金融预测方面的研究。本文采取2015年4月16日9点14分到2016年12月30日14点59分的分钟数据建立逻辑回归模型，利用最高价、最低价、收盘价、开盘价、成交量为样本数据，在预测前对数据进行统计分析，发现其呈尖峰后尾的分布，符合金融数据的特征。为了证明逻辑回归模型的预测效果，将原始数据集按照8：2的比例随机分成训练集和测试集，通过python编程得到逻辑回归模型进行预测，由得到的拟合结果可知逻辑回归模型在股指期货的预测中效果良好。但由于存在观测值缺陷，数据量不大，没有用同一数据集与其他模型进行对比，因此还需要大量的后续研究来得出更加精确合理的预测模型。