基于GP2X陀螺全站仪改正的井下双导线测量方法研究

何军泉

(温州市勘察测绘研究院，浙江 温州 325000)

随着GNSS测量的快速发展，地面平面控制网布设已经从传统全站仪导线测量逐步转换到GNSS静态测量，但井下贯通测量限制于其特殊的测量环境，依旧需要使用传统导线测量方法布设[1-3]。由于贯通测量常采用支导线测量，为提高测量成果的可靠性会采用单条路线往返测量的方法[4-5]，往返测量虽然可以通过二次测量确保测量成果中不出现粗差，但会存在两方面的问题：(1)支导线不存在闭合路线，测量成果精度较差；(2)由于井下测量存在视线差、道路坑洼多、视线折角大等不利因素，往返测量会极大地影响测量效率，长时间井下作业也会给测量人员产生隐形的不安全因素[6-8]。针对以上存在的问题，本文提出了基于GP2X陀螺全站仪改正的井下双导线测量方法，即利用高精度陀螺全站仪加测陀螺坚强边获得方向附和导线，以改正转折角的观测值，通过导线边归化改正精化观测点之间的距离观测值[9-12]，通过将推算的坐标与已知数据进行对比，检验测量精度。

1 虚拟双导线布设与测量

1.1 虚拟双导线布设

如图1所示，起始控制点为导线起算的已知控制点，终端点为导线测量的未知终点，K1，K2，K3，……，K15为常规导线布设的测量控制点，K1′，K2′，K3′，……，K15′为虚拟导线点，与上述控制点为一一对应关系。虚拟导线点号命名原则是与测量控制点进行对应，使测量人员与记录人员能快速找到测量导线与虚拟导线的点位关系。布设时，每间隔2～4个点虚拟导线必须与测量导线形成闭合环，以保证虚拟导线的可靠性。实际测量过程中K1′，K2′，K3′，…… ，K15′等虚拟控制点与K1，K2，K3，……，K15等导线控制点均为相同点位，在实测位置上没有区别，可假想虚拟控制点为无限接近导线控制点的成对的控制点。

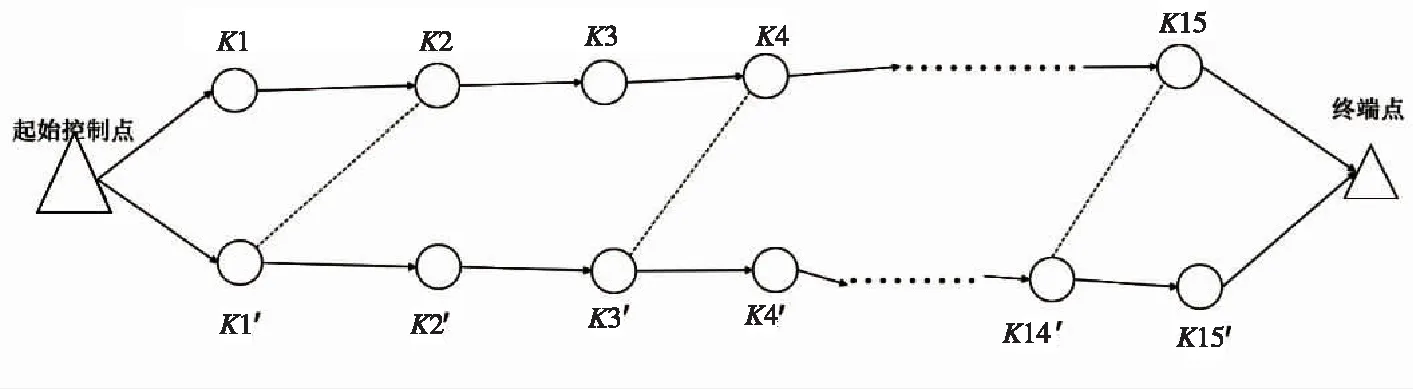
图1 井下虚拟双导线布设

1.2 虚拟双导线外业观测

以K3与K3′这一对对应点为例叙述外业观测步骤，其他点位观测方法依照此两点类推即可。

外业采集数据时应保证观测视线清晰、光线充足，将全站仪架设在K3点上，反射镜架设在K2、K4点上，选择K2方向为起始方向，按照盘左观测照准K2、顺时针照准K4、倒镜盘右观测照准K4、逆时针照准K2的读数顺序完成一测回的读数，获取水平角度、导线边长等测量数据，按此方法可进行K3点其他测回测量步骤。记录的转折角格式为K2-K3 -K4，表示以K3为顶点，K2顺时针转到K4的夹角。以上为K3点的测量步骤。

K3′点测量时，虽然与K3为同一点，但必须重新架设全站仪，完成独立的数据观测。按照盘左观测照准K4、盘左观测微动后照准K4′、顺时针照准K2′、倒镜盘右观测照准K2′、逆时针照准K4′、盘右观测逆时针微动后照准K4的读数顺序完成一测回的读数，获取水平角度、导线边长等测量数据，按此方法可进行K3′点其他测回测量步骤。记录的转折角格式为K4-K3′-K2′、K4-K3′-K4′，表示以K3′为顶点，K4顺时针转到K2′与K4′的夹角。这里特别说明，K2-K3 -K4是测量导线的常规测量转折角，K4-K3′-K2′、K4-K3′-K4′两个转折角的和实质上就是K2′-K3′-K4′这个虚拟导线的转折角，将虚拟导线转折角分两个小角测量的目的是将虚拟导线与测量导线连接形成闭合回路以便检查测量成果，提高控制网的可靠性。虽然K3与K3′两点位于同一个位置，但由于测量误差存在偶然性，实际测量时K3′会位于K3附近的随机位置。

2 井下导线布设与双导线测量成果

本文所使用的测量成果来自江苏某煤矿副井与风井之间的巷道贯通工程，在地面副井与风井附近各布设两个GNSS近井点，通过竖井联系测量向井下导入坐标系统。控制导线布设为7″首级控制导线，导线测量路线长度2.076 km，共有17个导线点，采用防爆型全站仪型号NIKON452-C，陀螺全站仪为索佳GP2X，标称精度均为2″、2 mm+2 ppm，测量导线具体布设情况如图2所示，由于虚拟导线与测量导线整体基本一致，未在图2中勾画虚拟导线，具体测量步骤参考1.2虚拟双导线外业观测，图中标记角度为1.2中提及的转折角，标记距离为归化改正后的导线点距离。需要说明一点，由于实际测量时永19(永19含义为永久控制点19)与永20之间出现了视线阻挡的情况，因此，取ZD作为转点进行测量，ZD不属于永久控制点，为保证其精度，在ZD与永20之间额外加测一次陀螺坚强边，此陀螺边的目的意在增强临时控制点的精度，与导线整体的陀螺控制无关，因此，本次计算时该陀螺边不参与导线解算，参与解算的陀螺边为永20-永21、永24-永25。

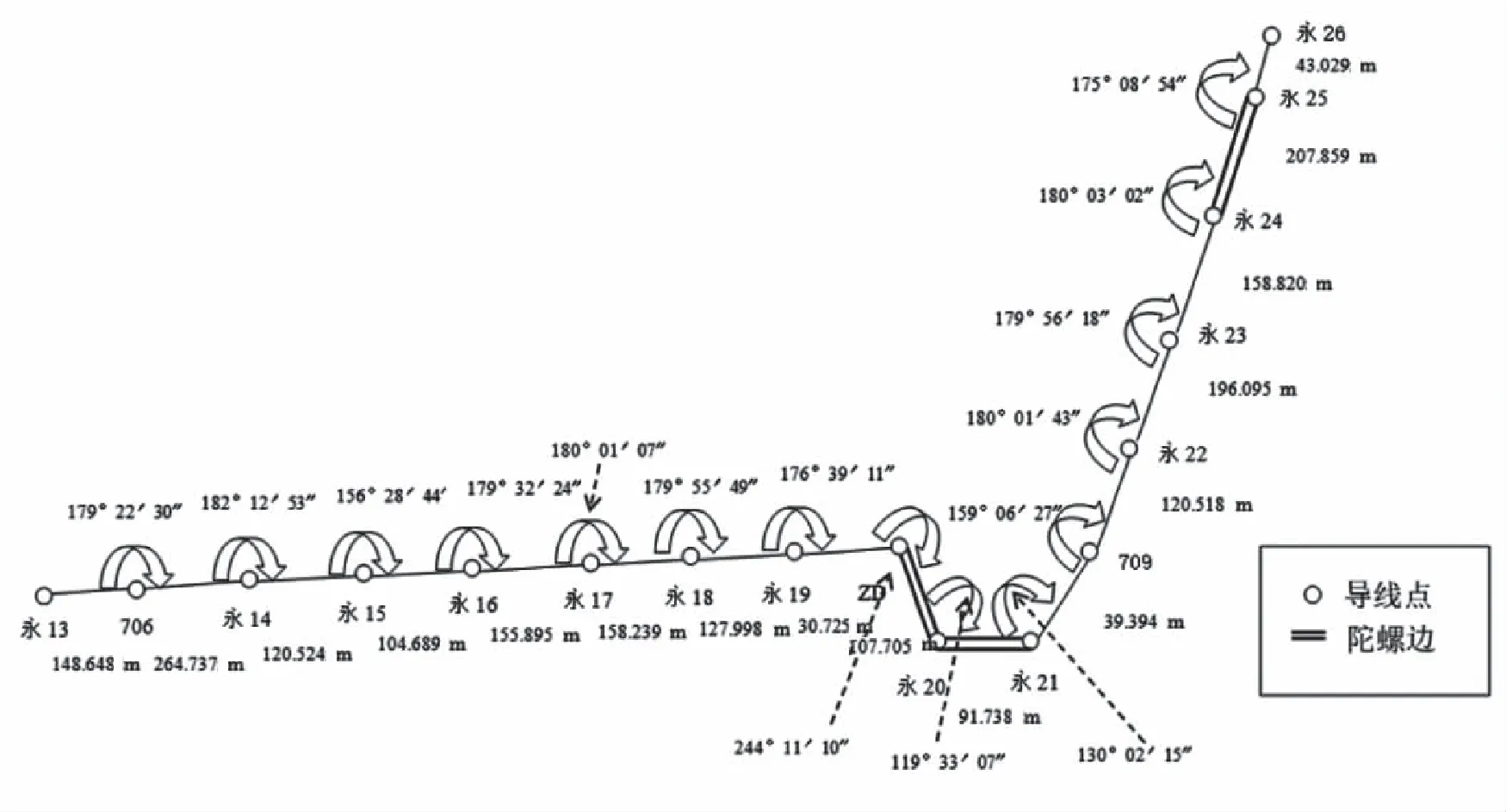
图2 井下导线测量布设

通过虚拟双导线技术单程对导线进行两次测量，结果如表1所示。通过对比发现两次测量结果非常接近，不存在粗差，因此，取两次测量平均值作为转折角测量的最终成果。

表1 双导线测量成果

距离测量取四次测量平均值后，还需进行归化改正，即化算到海平面及化归高斯投影面两项改正数。其中，导线边长化算到海平面的改正公式为：

ΔLM=-0.000 157Hl

(1)

式中，H为高程；l为未改正长度，m。当H为正时，ΔLM为负，反之亦然。

导线边长化归到高斯投影面的改正公式为：

(2)

式中，ym为导线边平均横坐标，即导线边中点到投影带中央子午线的距离，km；R为地球的平均半径，其值为6 371 km。导线边长归化改正结果列举如表2所示。

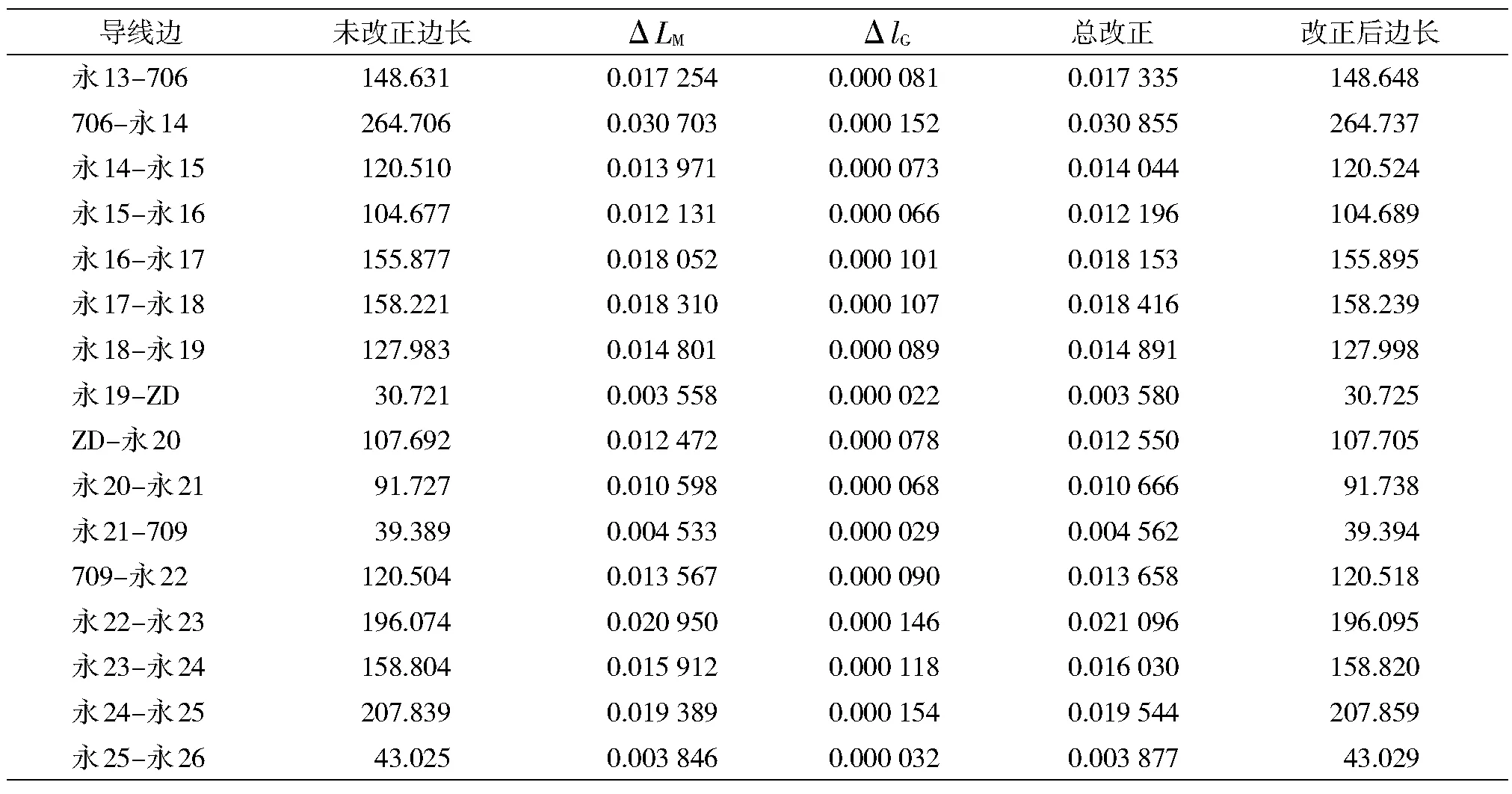
表2 导线边长归化改正成果/m

3 陀螺坚强边计算与使用方法

由于井下测量已知点数量不足，且测量环境差、转角多，容易出现已知数据不足、系统误差较大、短边测量引起误差增大等问题。陀螺全站仪能锁定真北方向，进而计算可以确定任意测边的坐标方位角，通过陀螺坚强边测量能够获得方向附和导线以提高测量精度。

与陀螺定向有关的方向主要有：陀螺北方向A′、真北方向A、坐标北方向α坐，陀螺仪的仪器常数Δ就是真北方向与陀螺北方向的差值，偏东为正，偏西为负。子午线收敛角γ是真北方向与坐标北方向之间的差值，偏东为正，偏西为负，三者关系如图3所示。

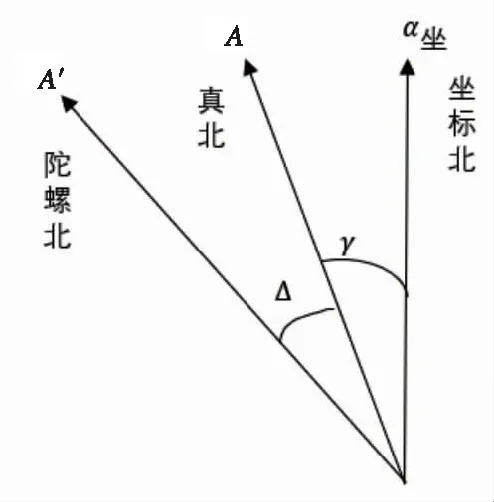
图3 陀螺北、真北、坐标北的关系示意图

由以上可知，想求得某未知边的坐标方位角，需先求得陀螺仪仪器常数与子午线收敛角。然后加入测量得到的陀螺方位角，可按以下公式求得坐标方位角：

α坐=A′+Δ-γ

(3)

式中，α坐为坐标方位角；A′为陀螺方位角；Δ为陀螺仪的仪器常数；γ为子午线收敛角。

依据《隧道贯通测量技术要求》，陀螺定向技术要求如表3所示。

表3 陀螺定向的主要限差

测量陀螺定向边的步骤如下：

(1)在井上已知边上测定仪器常数：测定仪器常数进行四次，每次三个测回，2次读数，规程要求各次之间的互差小于40″。

(2)在井下定向边上测定陀螺方位角：要求测定定向边陀螺方位角应进行三次下放，3次读数，其互差小于40″。

(3)在井上已知边重新测定仪器常数：测定仪器常数共进行两至三次，每次三个测回，1次读数，互差小于40″。

3.1 子午线收敛角的计算

测量仪器常数使用地面已知边I03-I04，陀螺边为永20-永21、永24-永25，因此，需计算I03、永20、永24三点的子午线收敛角。计算前需已知所用三点的坐标值(概略坐标即可，不需要太准确)，如表4所示。

表4 子午线收敛角计算所用已知点坐标值/m

子午线收敛角计算公式：

γ=K·y

(4)

式中，K为子午线收敛角系数；y为控制点Y坐标值。需要注意此处的Y坐标应去除带号，换算成km单位并减去500 km。将X坐标值换算为km后，根据具体数值查子午线收敛角系数表以获取值。现以I03点为例详细介绍计算过程：

由表4获知I03点坐标值(表4中已去掉带号)，首先，处理Y坐标，495 010.8×0.001-500=-4.99，即完成了Y坐标的单位转换与减去500 km，计算结果如表5所示。X坐标换算单位：3 856 672×0.001=3 856.672，查子午线收敛角系数表可知3 800 km(结果3 856.672 km的取整结果)对应计算系数为0.367 7和125，0.367 7+125×0.000 1×(3 856.672-3 800)×0.01=0.375，此结果即为子午线收敛角系数的值，结果如表5所示。然后根据式(4)可得子午线收敛角的以分为单位的小数值，换算为分秒结果如表5所示。

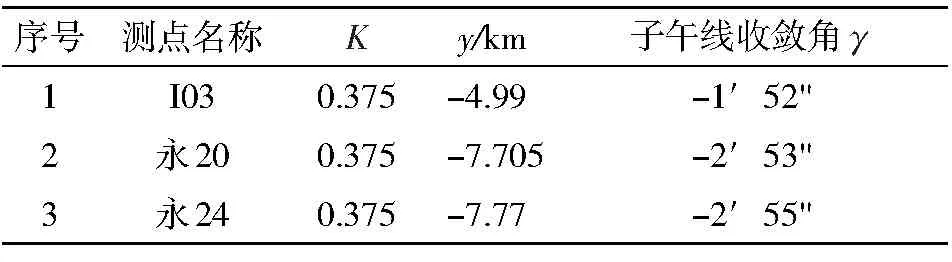
表5 子午线收敛角计算成果

3.2 陀螺仪器常数与坐标方位角计算

为测量永20-永21测边，在已知边I03-I04上进行7次测量，得到7次测量的陀螺方位角，由于子午线收敛角和坐标方位角已知，根据式(3)可计算得到每次测量的仪器常数，并计算仪器常数平均值，仪器常数与平均值的差值为V，如表6所示。由于篇幅原因，永24-永25测边所用仪器常数计算过程不再列出。

表6 陀螺经纬仪仪器常数计算表(I03-I04已知边)

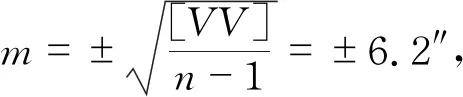
陀螺方位角观测值与陀螺定向边坐标方位角计算结果如表7所示，其中，永20-永21测边进行三次下放，永24-永25测边进行四次下放。

表7 坐标方位角计算表

由于永13-706边已知初始方向，根据计算所得陀螺方位角，根据图2可将导线整体划分为永13-永21，永20-永25，永25-永26三部分，其中，永13-永21，永20-永25均为起始、终末方向已知的导线，在测定方向上属于附和导线，可计算角度闭合差并反号平均分配到各转折角中，以提高导线测量的精度与可靠性。

4 精度对比

通过以上过程获得了导线边的转折角与距离，转折角通过方向附和导线的方法分配闭合差，距离进行了归化改正，可根据坐标正算公式推算各未知控制点的横纵坐标，并与已知控制点成果及无陀螺定向的导线测量进行对比，对比结果如表8所示。

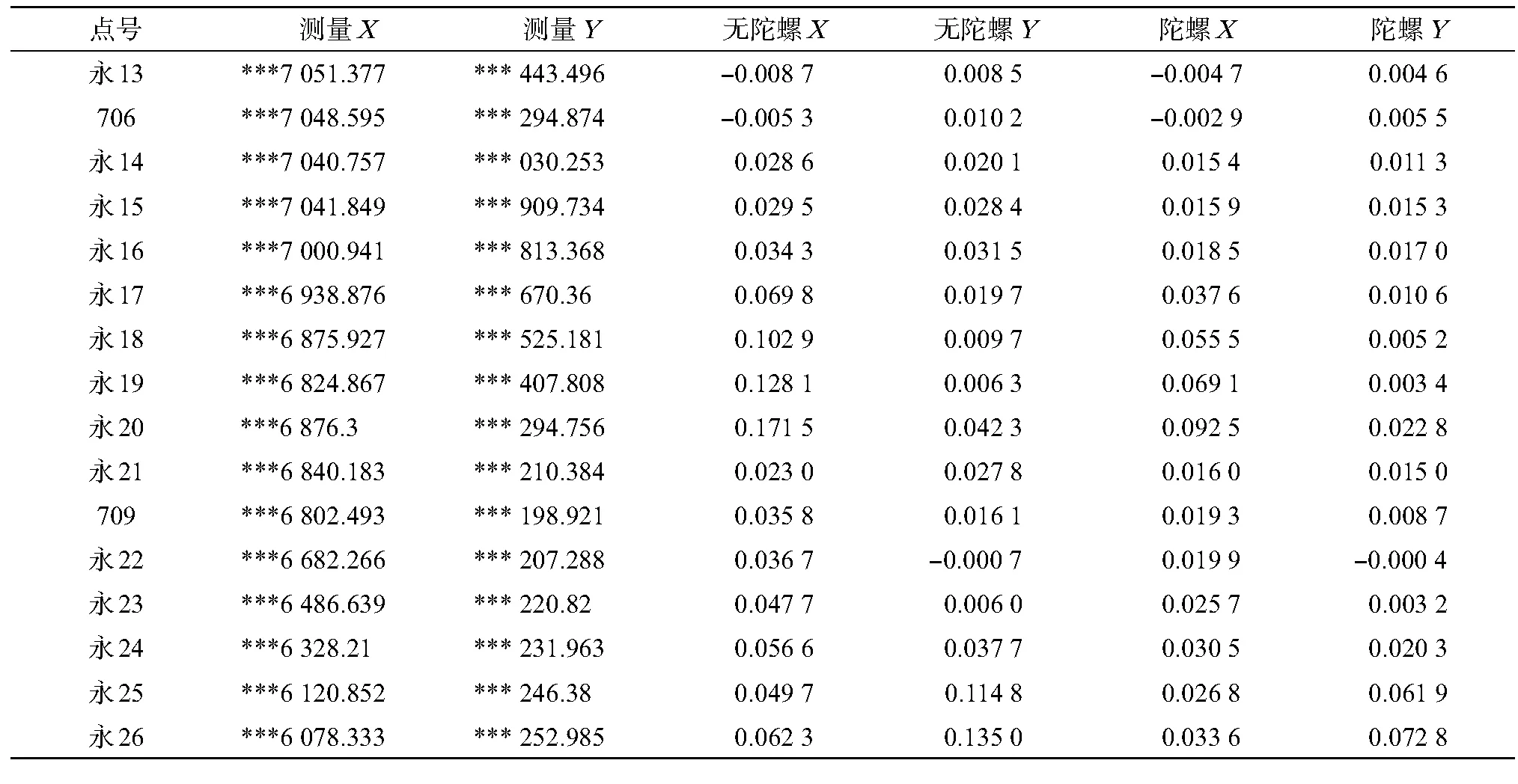
表8 坐标计算成果对比/m

计算X坐标无陀螺测量中误差为0.072 3 m，陀螺定向改正的测量中误差为0.039 3 m，计算Y坐标无陀螺测量中误差为0.050 7 m，陀螺定向改正的测量中误差为0.027 4 m，显然陀螺定向测量可以提高导线可靠性和测量精度。由于已知数据间隔时间较长，仅能作为概略数据参考，本次井下支导线测量坐标成果与概略坐标相差不大，可以认为测量的精度较高。

5 结 论

本文介绍了井下虚拟双导线的布设与测量方法，虚拟双导线技术可以相对往返测量提高工作效率，降低了埋点布设的难度，避免了测量人员长时间井下作业，提高了项目施工的效率与经济收益。从子午线收敛角计算开始，介绍了包括仪器常数计算方法、坐标方位角计算方法、导线边距离归化改正方法等技术，对井下导线测量进行了比较全面的精度控制。通过与已知数据计算对比，可以认为本次测量获得了比较高的精度，结果具有很强的可靠性。