基于参数贡献度的硬件安全分析方法在列控系统中的应用
高 莺
列车运行控制系统(以下简称“列控系统”)是集计算机、通信、控制、信号技术为一体,确保列车安全高效运行的系统,具有典型的计算机系统结构。例如,测速测距传感器、加速度传感器等传感输入信息,需要通过计算机系统,将列车的运行距离、速度、加速度等处理成能够被车载处理器识别的二进制信息,以便控制列车运行速度,确保行车安全;车载的各种制动实施信号、车门的关闭且锁闭信号等,也需要处理成二进制信息,以便及时实施制动或开/关门操作;另外,列控系统与司机、调度、维护等相关人员进行的人机交互,也需要由计算机系统完成。为此,本文通过分析计算机系统的安全特征来验证列控系统的安全性。
一些研究机构针对计算机系统(尤其是航空、军工等行业)各种组件的失效类型进行了总结和讨论,并形成了国际标准或商用数据库[1]。其中,很多标准按照失效致因机理的差别,将计算机系统的失效分为随机性失效和系统性失效[2]。系统性失效主要是由于系统需求和硬件设计错误导致的,需要在设计和实施阶段采用质量控制和检查流程等手段避免发生或及时予以纠正,可以看作是确定事件,只能进行定性分析;而随机性失效可以看作是一个或一系列随机事件,具有不确定性,在已知硬件元器件的失效率、失效模式和随机失效出现次数等基础上,可以对其量化,因此可以进行定量分析[3]。本文着眼于列控系统硬件安全性的定量分析,针对可能影响定量分析结果的参数,利用蒙特卡洛采样法对输入参数进行采样,得出不同的采样值,再对比分析不同参数对列控系统硬件安全性的影响。
1 系统安全分析原理
随着计算机事故致因机理及信号系统的复杂性不断提高,轨道交通行业的安全理念也不断发生转变,“危险”成为系统安全理念的核心。诸多国际标准中定义“危险”为“系统运行过程中,真实存在或可能出现的条件,这种条件下可能引发某个或一系列意外事件,导致人员伤亡、设备/财产损失、环境破坏、职业疾病的恶劣后果”[4]。危险不是系统的静止状态,而是系统行为与运行环境的耦合作用,即系统在某种环境或前因后果下的特定输出。列控系统是否安全,与设备的工作环境、子系统间接口、线路参数等紧密相关。系统安全保障的主线是在整个运行过程中对系统危险进行跟踪控制,其核心过程见图1[5]。
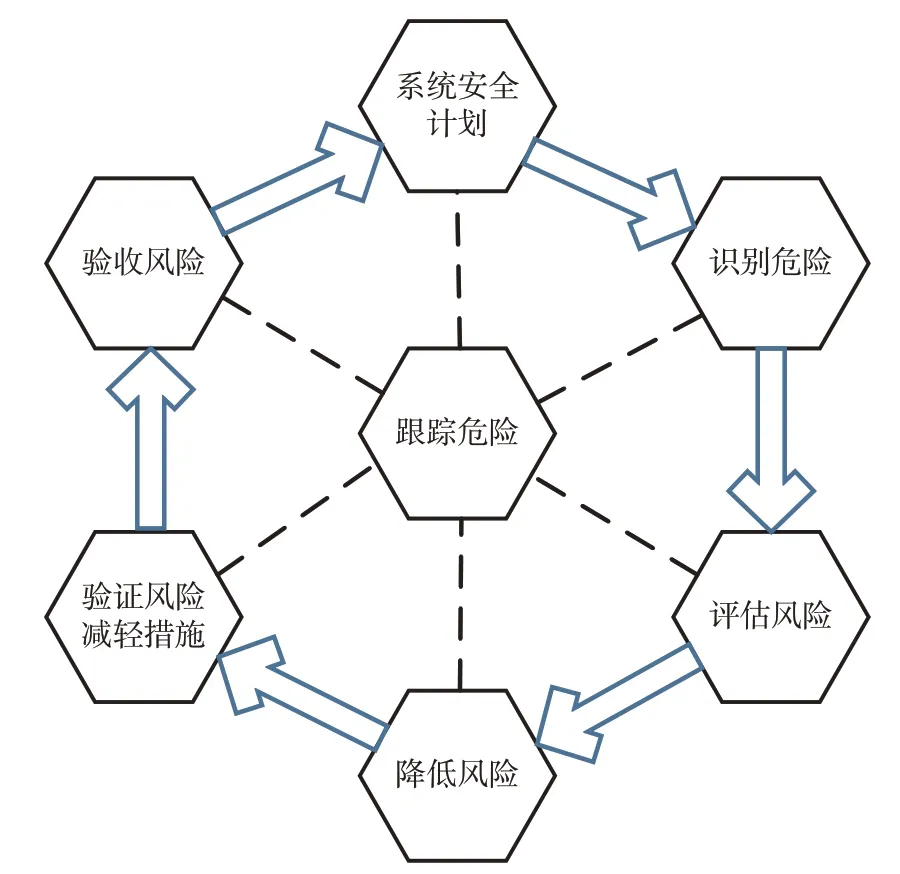
图1 系统安全保障核心过程
由于“安全”是相对的,因此可以用具体的量值表示危险程度,找出导致事故发生的潜在危险,并且用具体的数值来表示其发生的可能性,计算由其导致事故发生的概率和严重程度,制定对策和措施,从而预防事故的发生。
《电气、电子、可编程电子安全相关系统的功能安全》(IEC 61508)中规定了在低要求模式、高要求模式或连续模式下,需要分配给一个安全相关系统安全功能的目标失效概率区间。铁路信号系统属于“高要求模式或连续模式”,其量化指标为“每小时危险故障的平均频率(PFH)”。同时,“安全完整性”定义为“在规定的条件下和规定的时间内,安全相关系统成功实现所要求的安全功能的概率”。为了量化安全完整性,IEC 61508 提出了安全完整性等级(Safety Integrity Level, SIL)的概念,用于衡量系统是否具备达到所要求的安全功能的能力。SIL 分为5 个等级,SIL4 为最高等级,SIL0为最低等级,SIL值越高,安全相关系统在执行安全功能时失效的可能性越小,每一级SIL对应一个PFH的取值范围[6]。本文用SILXU表示SIL的等级,且为每一级SIL的上限。
2 列控系统安全计算机结构
本文选用列控系统安全计算机二乘二取二结构作为分析对象。该结构依据IEC 61508、EN 50129和EN 50128 标准,基于分层思想设计,逻辑上分成应用软件层、安全计算机软件层、实施多任务操作系统层和硬件层,如图2所示[7]。
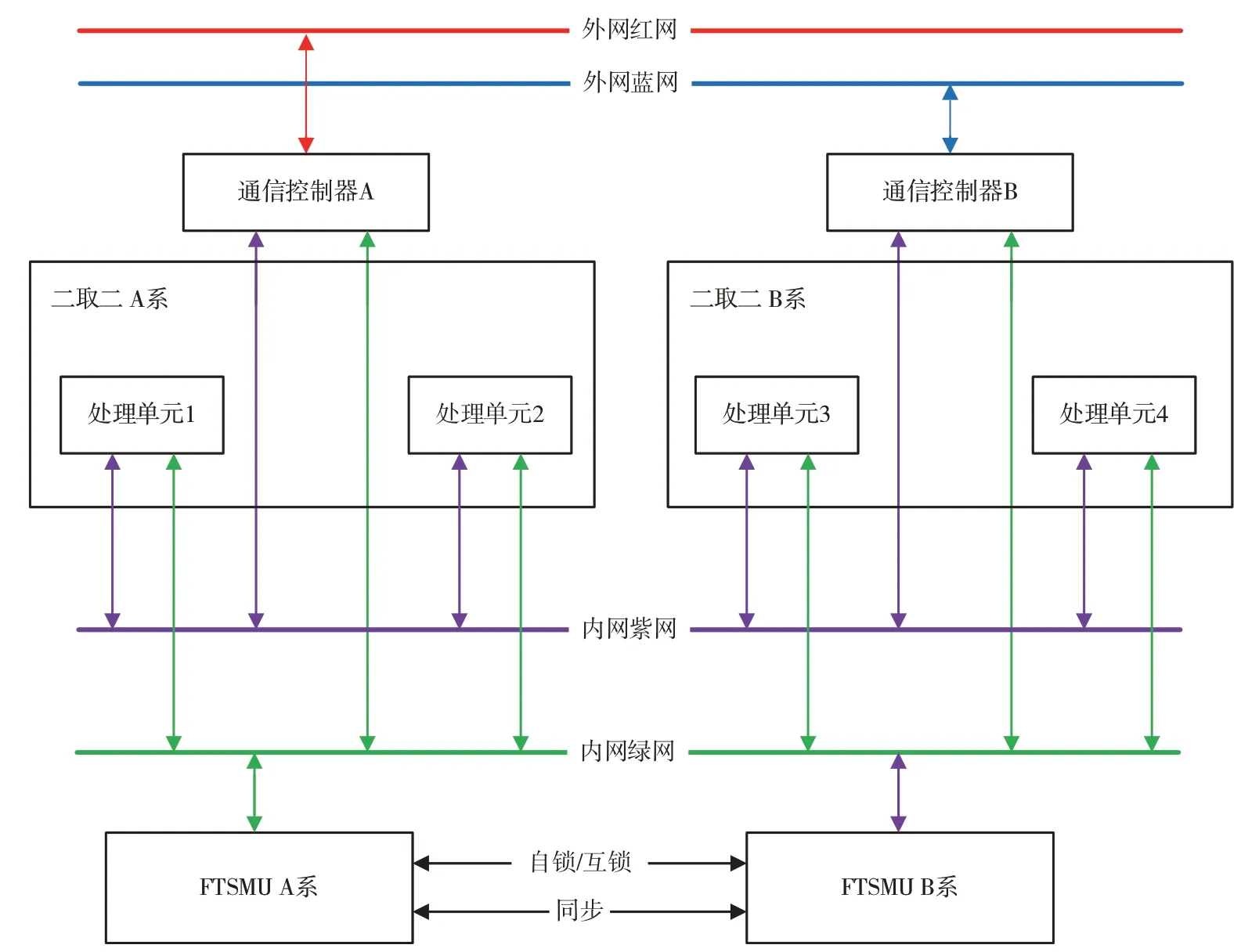
图2 列控系统安全计算机二乘二取二结构
FTSMU 容错及安全管理(Fault Tolerant and Safe Management Unit)机制是保证列控系统安全计算机安全性的基础。基于确定性原则设计,要求安全计算机在正确的时间执行正确的动作,并产生正确的结果,否则判错而导向安全。列控系统安全计算机接收的应用数据通过以太网外网,分别发送给通信控制器A 和B,二取二的A 系处理单元1 和2、二取二的B系处理单元3和4承载的列控应用软件,在FTSMU A 系和B系的控制下,通过冗余的以太网内网,读取通信控制器A和B中的应用数据并进行处理[8]。
3 基于参数贡献度的PFH分析方法
IEC 61508-6 提供的几种安全苛求系统的PFH常用计算方法,均可以将PFH表示为参数MTTR、λD、β、βD、DC的 函 数 , 即PFH=Φ(MTTR,λD,β,βD,DC)[6]。其中:MTTR为系统平均故障恢复时间;λD为单位时间内(每小时)危险侧的失效概率,可以表示为λD=λDU+λDD;λDU表示未检测到的危险侧失效概率;λDD表示检测到的危险侧失效概率;β为未检测到的共因失效因子;βD为检测到的共因失效因子;DC为诊断覆盖率 , 与λDD、λDU的 关 系 为λDU=λD(1-DC),λDD=λD·DC。
蒙特卡洛采样法是常见的用来分析随机变量不确定的方法,本文采用蒙特卡洛采样法获得PFH计算中需要抽样的样本值。
定义1:设x为随机变量,其累积分布函数为F(x),则其逆函数为[9]
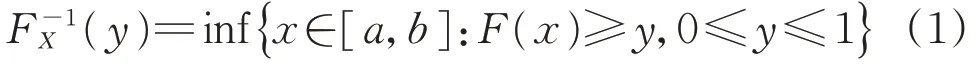
通过逆变换算法获得随机变量x的样本值:①根据随机变量x的概率密度函数,计算其累计分布函数F(x);②求F(x)的反函数F-1(x);③设置随机变量Z,Z在(0,1)范围内服从均匀分布,即Z~Uniform(0,1);④令Z=F(x),通过随机数发生器获得随机数Z;⑤计算样本值X,X=完成随机变量x的样本抽样。
假设PFH计算中输入的参数MTTR,λD,β,βD,DC都是不确定的,将它们依次表示为X1,X2,X3,X4,X5,通过蒙特卡洛采样法均匀采样n次,获得输入参数的数据样本Xi,即Xi=(xi1,xi2,…,xin),i=1,2,3,4,5;用Yi表示输出数据样本,即PFH的样本,将输入参数的数据样本Xi代入PFH=Φ(MTTR,λD,β,βD,DC)可获得输出数据样本Yi,并得到输出样本分布fY(y)=(Y1,Y2,…,Yn)[10]。
定义2:FY为输出数据样本中PFH高于SILXU的累积分布概率,则
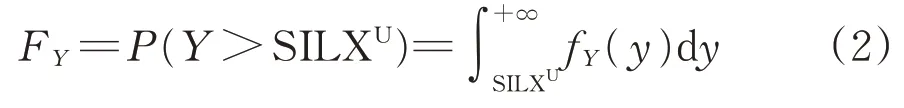
定义 3:FY|Xi=xˉi为在Xi=xˉi条件下的输出数据样本中PFH高于SILXU的累积分布概率,则

利用式(3)可以计算输入参数Xi的不确定性,对系统的安全完整性等级影响的贡献度Ci:

式中,ΔF=FY-FY|Xi=xˉi。
图3 表示消除了输入参数的不确定性后,ΔF的3种典型情况,具体说明如下。
1)ΔF=FY,此时Ci=1,输出数据全部分布在规定的SILX 区域内,见图3(a)。表明输入参数不确定导致硬件安全完整性等级不确定的概率为100%,即输入参数完全影响硬件安全完整性等级。
2)ΔF=0,此时Ci=0,输出数据不在SILX区域内的部分累积分布与输入参数不确定时的累积分布相同,见图3(b)。表明输入参数不确定导致硬件安全完整性等级不确定的概率为0,即输入参数对硬件安全完整性等级没有影响。
3) 0< ΔF< 1,此时 0<Ci<1,输出数据不在SILX 区域内的部分累积分布大于输入参数不确定时的累积分布,见图3(c)。表明输入参数的不确定导致硬件安全完整性等级不确定性的概率为0~100%,即输入参数对硬件安全完整性等级有积极影响。
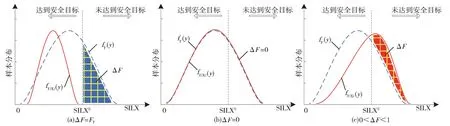
图3 ΔF典型情况
通过上述3 种典型情况分析可知:Ci值越大,相应的输入参数对硬件安全完整性等级的影响越大。
4 实例应用及分析
在列控系统安全计算机二乘二取二结构下,分析MTTR,λD,β,βD和DC这 5 个输入参数对硬件安全完整性等级影响的贡献度。假设各输入参数服从均匀分布,通过蒙特卡洛采样法得到输入数据的样本,每次采样获得样本个数为10 000,各输入参数取值为:MTTR~U(0.5,24);λD~U(5e-8,1e-6);β~U(0.02,0.2);βD~U(0.01,0.1);DC~U(0.9,0.99)。
4.1 MTTR对SILX的影响
令λD、β、βD、DC不变,通过蒙特卡洛采样法,分别获得MTTR在不确定条件下的PFH输出数据样本及其累积分布函数,见图4。假定二乘二取二结构硬件的安全目标为SIL4,即SIL4U=1e-8。由图4 可知,MTTR不确定时,PFH输出数据不在SIL4 区域内部分的累积分布与MTTR确定时的情况相同,即CMTTR=0,则MTTR不会对硬件的安全完整性等级的取值产生影响。

图4 MTTR在不确定条件下对硬件SIL影响的贡献度分析
4.2 λD 对 SILX 的影响
令MTTR、β、βD、DC不变,分别获得λD在不确定条件下的PFH输出数据样本及累积分布函数,见图5。假定2 乘2 取2 结构硬件的安全目标为SIL4,由图5 可知,λD不确定时,PFH输出数据全部分布在规定的SIL4 区域内,即CλD=1,可知λD完全影响硬件的安全完整性等级。如果希望硬件的安全完整性等级达到SIL4,首先需要控制好λD的取值。
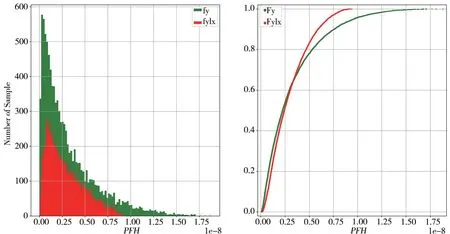
图5 λD在不确定条件下对硬件SIL影响的贡献分析
4.3 β 对 SILX 的影响
令MTTR、λD、βD、DC不变,分别获得β在不确定条件下的PFH输出数据样本及累积分布函数,见图6。假定安全目标为SIL4,由图6可知,β不确定时,PFH输出数据不在SIL4 区域内部分的累积分布大于β不确定时的累积分布。同时,根据公式(4),通过Python 工具进行计算可得Cβ=0.8610,可知β对硬件的安全完整性等级有积极影响。如果希望硬件的安全完整性等级达到SIL4,需要关注β的取值。

图6 β在不确定条件下对硬件SIL影响的贡献分析
4.4 βD对SILX的影响
令MTTR、λD、β、DC不变,分别获得βD在不确定条件下的PFH输出数据样本及累积分布函数。假定安全目标为SIL4,则βD不确定时,PFH输出数据不在SIL4 区域内部分的累积分布与MTTR确定时相同,CβD=0,可知βD不会对硬件的安全完整性等级的取值产生影响,其对SIL 影响的贡献分析曲线与图4类似。
4.5 DC对SILX的影响
令MTTR、λD、β、βD其他输入参数不变,分别获得DC在不确定下的PFH输出数据样本及累积分布函数。假定安全目标为SIL4,DC不确定时,PFH输出数据不在SIL4 区域内部分的累积分布大于β不确定时的累积分布。通过Python工具计算可得,CDC=0.8568,可知DC对硬件的安全完整性等级有积极影响,其对SIL 影响的贡献分析曲线与图6 类似。如果希望硬件的安全完整性等级达到SIL4,需要关注DC的取值。
综合上述分析结果,可得到各输入参数在二乘二取二结构下对硬件安全完整性等级影响的贡献度大小,如表1所示。

表1 二乘二取二结构中输入参数对硬件SIL影响的贡献度
通过表1 可知:在二乘二取二结构下,CλD>Cβ>CDC>CMTTR/CβD,即λD对 SILX 的影响最大,β和DC有一定影响,λD和MTTR几乎没有影响。这是因为:λD指向危险侧失效概率,表示的失效是导向危险的,因此在系统安全性中是最需要关注的指标;β指向没有检测到的共因失效,由于是没有检测到的失效,所以有潜在的风险,也是需要关注的;DC指向能够检测到的危险侧失效率,因此对安全性的影响比λD和β小。相比之下,βD指向可以检测到的共因失效,贡献度比β小;MTTR是系统平均故障恢复时间,在系统可靠运行周期中所占比重很小,因此对系统安全性的影响最小。
5 结束语
本文以安全完整性等级作为衡量列控系统安全性的指标,分析了二乘二取二结构中不同输入参数对其安全性的影响。为了避免单一的分析结果缺乏说服力,采用蒙特卡洛分析法对所有的输入参数进行采样,得出一组不同的采样值,再逐一分析每一个参数在其他输入参数不变的条件下,对列控系统安全完整性等级的贡献度。该分析结果对列控系统研发人员在设计产品的性能指标及参数的选择方面具有一定的参考意义。定量的安全分析能够为控制随机性失效,识别产品中的安全薄弱环节,找到影响安全指标的关键部件提供参考依据,指导设计进行针对性优化和失效防护。

