基于一维综合孔径微波辐射计的大气海洋环境参数敏感性分析

冯梦延, 艾未华, 刘茂宏, 陈冠宇, 陆 文

基于一维综合孔径微波辐射计的大气海洋环境参数敏感性分析

冯梦延1, 艾未华1, 刘茂宏1, 陈冠宇2, 陆 文1

(1. 国防科技大学 气象海洋学院, 江苏 南京 210000; 2. 中国人民解放军32033部队, 海南 海口 570100)

相比于实孔径微波辐射计, 一维综合孔径微波辐射计具有高空间分辨率和多入射角观测特点。本文提出采用观测频率为6.9, 10.65, 18.7, 23.8和36.5 GHz, 且入射角范围为0°～65°的一维综合孔径微波辐射计遥感大气海洋环境要素。基于构建的微波大气海洋辐射传输正演模型, 分析了辐射计亮温对大气海洋环境要素的敏感性, 为辐射计关键指标确定和大气海洋环境要素反演算法设计提供技术支撑。结果表明: 一维综合孔径微波辐射计的垂直和水平极化亮温对大气海洋环境要素的敏感性表现出不同特性, 且敏感性随入射角的改变而变化显著; 6.9和10.65 GHz对海面温度的敏感性较大, 且随着入射角的增大, 垂直极化亮温的敏感性增大, 水平极化亮温的敏感性减小; 10.65和18.7 GHz对海面风速的敏感性相对较大, 且敏感性最大的风速区间位于10～20 m/s; 23.8 GHz对大气水汽含量最敏感, 且水汽含量较低、入射角较大时, 敏感性越大; 36.5 GHz对云液态水含量最敏感, 随着入射角的增大, 垂直极化亮温的敏感性减小, 水平极化的敏感性增大, 但两者均在液态水含量较小时表现出较大的敏感性。

一维综合孔径微波辐射计; 高空间分辨率; 多入射角; 敏感性分析

地球表面约三分之二的面积被海洋覆盖。获取海洋环境信息对研究全球气候具有重要的作用。虽然浮标等测量方式可以获得较高精度的海洋环境信息, 但是其不能满足长期的, 大尺度范围的数据需求[1]。因此, 利用微波辐射计获取海面温度、海面风场、大气水汽含量和云液态水含量成为重要方式[2-4]。

目前, 可以提供海洋环境产品的星载微波辐射计主要包括TMI、WindSat、AMSR2、HY-2, 其均为实孔径微波辐射计, 且入射角为一个定值。由于空间分辨率和天线尺寸成反比, 导致传统实孔径微波辐射计的空间分辨率较低。例如, WindSat和AMSR2上的C波段通道, 其空间分辨率大约为50 km[5-6]。所以, Schanda提出了将综合孔径方法应用到遥感领域来解决空间分辨率与天线物理尺寸之间的固有矛盾[7], 其原理与综合孔径射电望远镜类似[8]。

一维综合孔径微波辐射计用一维的小孔径天线阵列代替大的实孔径天线, 对相隔一定距离的天线对进行复相关运算可以测量场景辐射的空间频率分量[9]。小天线观测信号的复相关输出称为可见度函数, 通过对可见度函数进行傅里叶变换获得亮温图像[10]。相比于实孔径微波辐射计, 由于不同小天线对应不同的入射角, 其合成的亮温图像是在多个入射角处的亮温组合。图1为星载一维综合孔径微波辐射计的观测示意图。

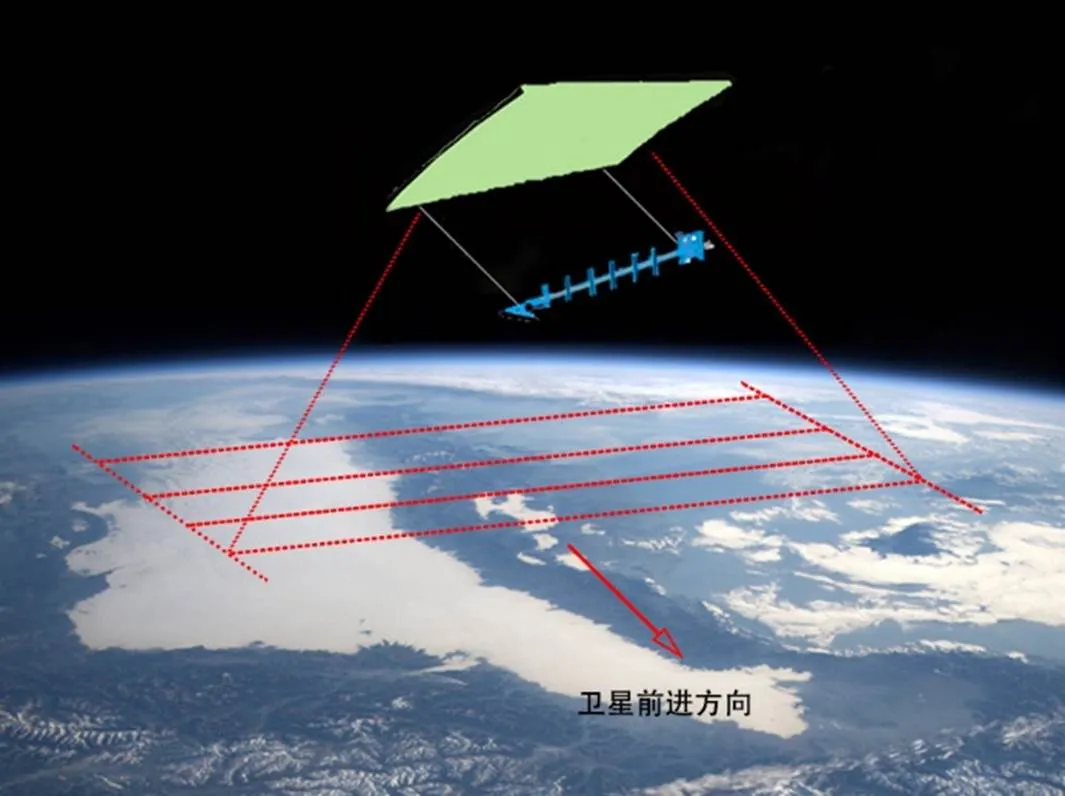
图1 星载一维综合孔径微波辐射计的观测示意图

为了获取高空间分辨率的海洋环境产品, 本文提出采用星载一维综合孔径微波辐射计获得海洋环境参数。假设该一维综合孔径微波辐射计的观测频点为: 6.9、10.65、18.7、23.8和36.5 GHz, 且每个频点为、双极化模式。由于场景辐射亮温随入射角变化很大, 例如当入射角出现1°的误差时, 海面温度的反演值会出现6 ℃的误差[6], 所以, 对于一维综合孔径微波辐射计, 在不同入射角处研究亮温对海洋环境要素的敏感性具有重要意义。目前, 许多学者针对固定入射角的实孔径微波辐射计开展了一系列敏感性研究[11-12]; 陈冠宇等针对C波段的单频点一维综合孔径微波辐射计, 开展了若干入射角的敏感性分析[13]。本文基于辐射传输正演模型, 仿真了5个频点在0°～65°入射角范围内的辐射亮温。其次, 计算了0°～65°入射角范围内亮温对海面温度、海面风速、海面风向、水汽含量和云液水含量的敏感性。

1 海洋大气辐射传输正演模型

如图2所示, 大气顶向外出射的辐射亮温T, p可以表示为[14-15]:

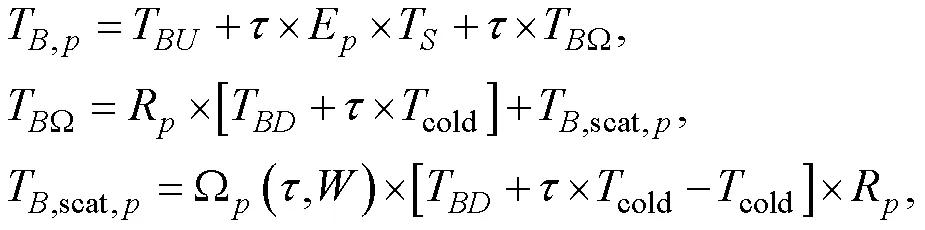
其中, p为极化方式, p = v, h。TBU和TBD分别表示大气辐射的上行和下行亮温, τ为整层大气透过率, Ep为海面发射率(由海面发射率模型计算)。TS为海面温度。Rp=1–Ep表示海面反射率。TBΩ为大气下行亮温和宇宙背景亮温被海面反射和散射的辐射值。Tcold为宇宙背景亮温, 通常取2.73 K。Ωp表示被海面散射下行辐射的经验校正系数, 与频率f, 入射角θ, 透过率τ和风速W有关。TB, scat, p表示非平静海面对大于或小于入射角方向的大气辐射亮温的散射作用。

1.1 海面发射率模型

海面发射率模型是本文研究的基础。目前, 计算海面发射率的物理模型主要包括: 双尺度模型[16]、光学模型[17]和小斜率近似模型(SSA)[18]。这些模型计算复杂且精度较低, 不能满足研究需求。本文采用Meissner等建立的海面发射率模型[14], 该模型是以星载微波辐射计WindSat、SSM/I F13亮温数据, QuikSCAT、ncep、HRD的风速风向数据以及Reyno­lds OI 海面温度数据等为基础构建的经验海面发射率模型。该模型可以计算0°～65°入射角范围内和–2～ 40 ℃海面温度范围内的海面发射率E[14]。该模型将海面发射率分成3个部分, 分别为平静海面发射率0, p, 由风速引起的发射率增量ΔE, p和由风向引起的发射率增量Δ, p。如下所示:

E=0, p+ ΔE, p+ Δ, p, (2)

其中,0, p是频率, 入射角, 海面温度T和海面盐度的函数, 由Fresnel定律计算得到[14, 19]。ΔE, p和Δ, p分别与风速和风向有关, 具体算法参考[14]。

1.2 大气吸收发射模型

在非降水大气条件下, 气溶胶等粒子对微波的散射可以忽略。在低于100 GHz的频率范围内, 主要的吸收成分为氧气、水汽和液态水。T,T和可以根据大气廓线计算得到[20-21]。由于该方法计算速度慢, 本文采用Wentz经验模型[6]计算T,T和[6], 其以频率, 入射角, 海面温度T, 总柱液态水含量和总柱水汽含量为输入。需要说明的是, 由于该模型[6]中计算云液态水吸收系数的算法需要输入云的平均温度T, 且该数据很难获得, 所以, 本文采用公式(3)计算云液态水吸收系数[12]:

A=b0(1+b1)。 (3)

一维综合孔径微波辐射计同时观测目标场景在多个入射角的辐射值, 且各个方向的辐射值相互独立。本文采用的辐射传输正演模型适用于一维综合孔径微波辐射计系统。金梦彤等利用微波辐射传输正演模型[22]仿真了星载一维综合孔径微波辐射计遥感海面盐度的亮温值[23]; 刘泽霖[24]在研究综合孔径微波辐射计反演大气温度廓线时也采用了DOTLRT模型[25]仿真了亮温值。

2 亮温对大气海洋环境要素的敏感性分析

为了定量计算亮温对海洋环境要素的敏感性大小, 本文假设了5个环境场, 如表1所示。以环境场为基础, 用辐射传输正演模型计算大气顶出射的辐射亮温, 根据公式(4)计算亮温对大气海洋环境要素敏感性。由于海水盐度对该一维综合孔径微波辐射计的观测频率影响很小, 本文将海水盐度设为常数。海面风速和海面风向为海面10 m风速和风向。风向为风矢量与卫星观测方位的夹角, 顺风时为0°, 逆风时为180°。

表1 大气海洋环境要素值

2.1 亮温对海洋环境要素的敏感性分析

海洋环境要素的变化会直接影响海面发射率的变化, 从而造成辐射计观测亮温的改变。在不同入射角处, 不同的观测频率对海洋环境要素的敏感性不同。理论上, 敏感性越大, 反演精度越高。本节首先计算亮温对海洋环境要素的敏感性系数, 根据场景1, 2, 3, 利用辐射传输正演模型分别计算亮温对海面温度, 海面风速, 海面风向的敏感性系数。

2.1.1 海面温度敏感性分析

图3为亮温对海面温度在0°～65°入射角范围内的敏感性。从图3可以看出, 垂直极化亮温对海面温度的敏感性略大于水平极化亮温。6.9 GHz和10.65 GHz对海面温度的敏感性表现相似且6.9 GHz和10.65 GHz对海面温度的敏感性较高。6.9和10.65 GHz的垂直极化和水平极化亮温对海面温度的敏感性随海面温度的增加而增加, 但是18.7, 23.8, 36.5 GHz的垂直极化和水平极化亮温对海面温度的敏感性随海面温度先减小后增加, 如图3i和3j所示, 敏感性系数的最小值没有出现在海面温度最小值处。

6.9和10.65 GHz的垂直极化亮温对海面温度的敏感性随入射角的增加而增加, 其水平极化亮温对海面温度的敏感性随入射角的增大而减小。18.7, 23.8, 36.5 GHz的垂直极化亮温对海面温度的敏感性与入射角的关系在不同的海面温度范围内表现不同。例如, 图3g中显示, 在T<283 K内, 敏感性随入射角的增大先减小后增大, 但是在283≤T≤313 K内, 敏感性随入射角的增大持续增大。总体上, 18.7, 23.8, 36.5 GHz的水平极化亮温对海面温度的敏感性随入射角的增大而减小。36.5 GHz的水平极化亮温对海面温度的敏感性在低海面温度处达到最大, 这与其他频点的表现相反。

从海面温度反演的角度分析, 6.9 GHz是核心频率, 其次是10.65 GHz, 这与许多研究者得到的结论一致[6, 26-28]。垂直极化亮温对海面温度反演的贡献主要在高海温和大入射角处。36.5 GHz垂直极化亮温在T≤278 K和0°≤≤30°也有较大的贡献。除了36.5 GHz, 水平极化亮温对海面温度反演的贡献主要在高海温和小入射角处, 而36.5 GHz水平极化亮温对海面温度反演的贡献主要在低海温和小入射角处。

2.1.2 海面风场敏感性分析

图4为亮温对海面风速在0°～65°范围内的敏感性。从图中可以看出, 水平极化亮温对海面风速的敏感性大于垂直极化亮温。总体来看, 10.65, 18.7和36.5 GHz对海面风速的敏感性较大, 23.8 GHz的敏感性最小。在12 m/s≤≤25 m/s和0°≤≤45°范围内, 垂直极化亮温对海面风速的敏感性较大。10.65, 18.7和36.5 GHz垂直极化亮温对海面风速的敏感性大于6.9和23.8 GHz。在25 m/s≤≤30 m/s范围内, 垂直极化亮温对海面风速的敏感性随海面风速的增加几乎不变, 这说明在25 m/s≤≤30 m/s范围内, 风速与亮温呈线性关系, 但是其随入射角的增大而减小。

所有频点的水平极化亮温对海面风速的敏感性表现相似。与垂直极化亮温相比, 水平极化亮温对海面风速的敏感性在0 m/s≤≤5 m/s和55°≤≤65°范围内也存在极大值。例如, 在图4f中, 当风速为1 m/s且入射角为65°时, 水平极化亮温对海面风速的敏感性为1.902 1 K/(mּs–1)。与垂直极化亮温类似, 在25 m/s≤≤30 m/s范围内, 水平极化亮温对海面风速的敏感性随海面风速的增加几乎不变, 但是其随入射角的增大而增大。

具有较大敏感性的区间, 其海面风速反演精度更高。综上所述, 6.9, 10.65, 18.7 GHz垂直极化亮温对反演海面风速的贡献主要在10 m/s≤≤30 m/s和0°≤≤45°。23.8, 36.5 GHz垂直极化亮温对反演海面风速的贡献主要在10 m/s≤≤25 m/s和0°≤≤35°。6.9, 10.65, 18.7和36.5 GHz水平极化亮温对反演海面风速的贡献主要在12 m/s≤≤30 m/s和0°≤≤65°; 0 m/s≤≤5 m/s和50°≤≤65°。23.8 GHz水平极化亮温对反演海面风速的贡献主要在10 m/s≤≤25 m/s和0°≤≤45°; 0 m/s≤≤5 m/s和50°≤≤65°。

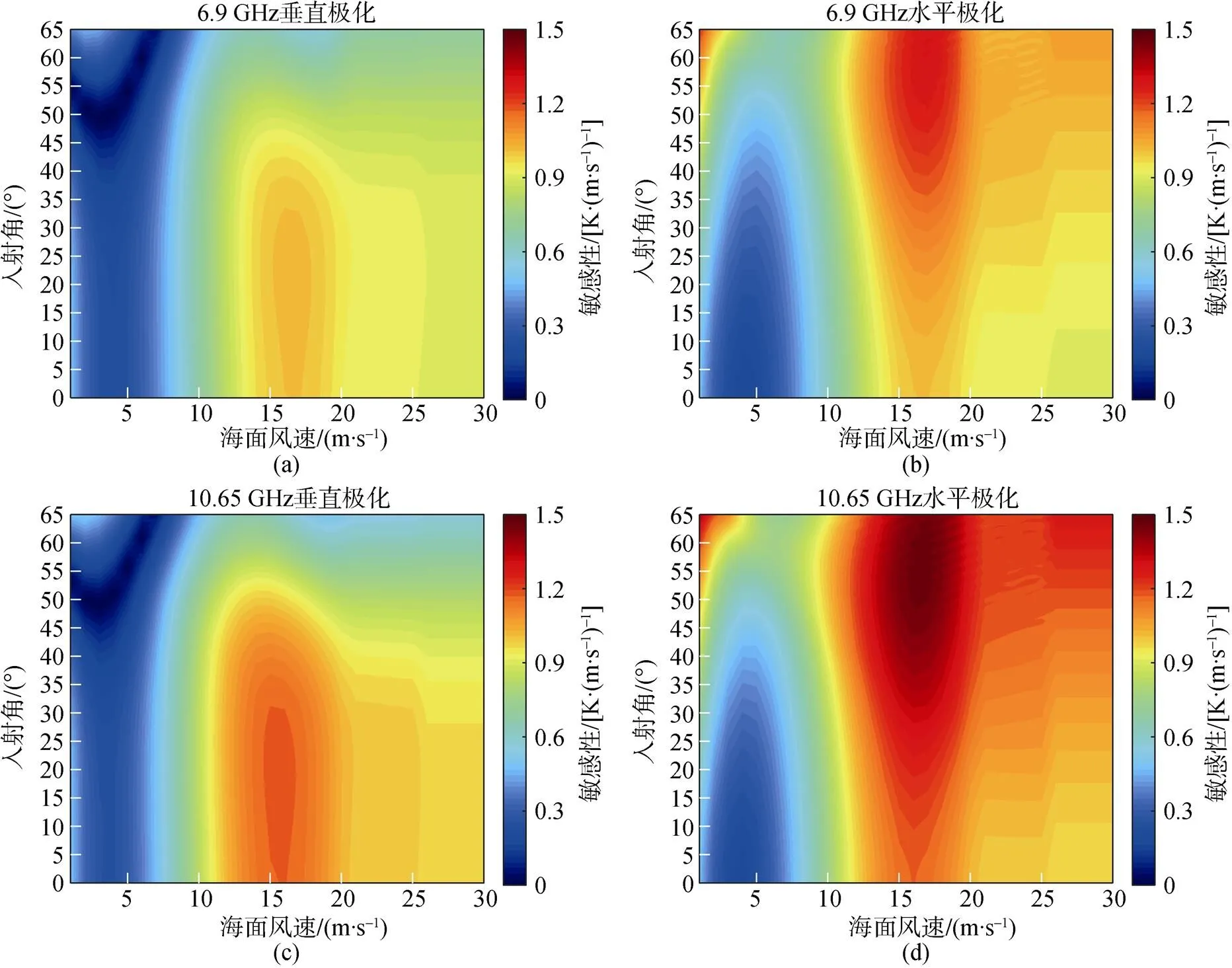
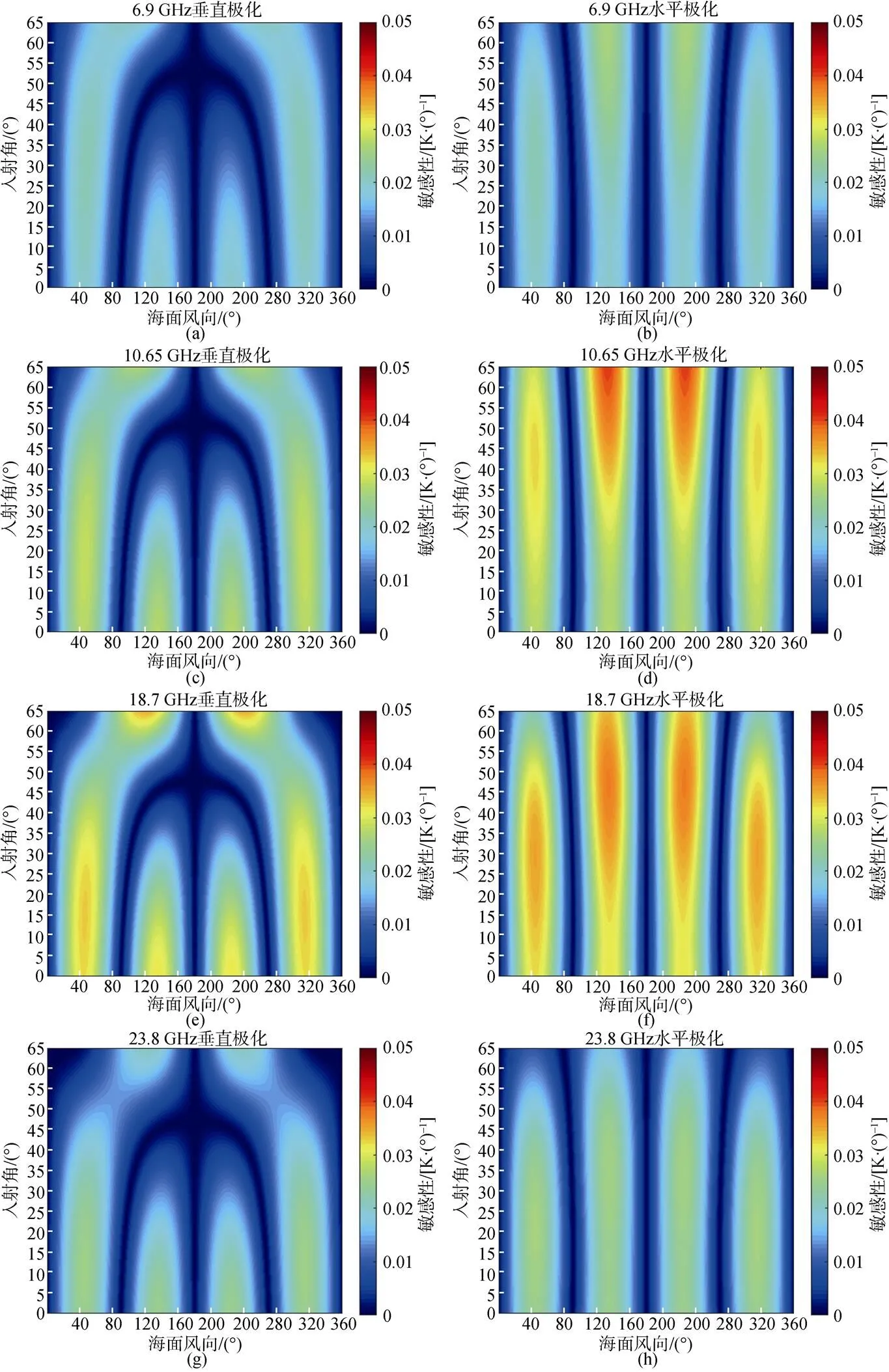
图5为亮温对海面风向在0°～65°内的敏感性。从图中可以看出亮温对海面风向的敏感性较小。图5为轴对称图形且对称轴为≤180°。18.7和36.5 GHz的垂直极化和水平极化亮温对海面风向的敏感性较高, 但是最大值均小于0.05 K/°。

2.2 亮温对大气参数的敏感性分析

根据无散射条件下的辐射传输方程, 星载一维综合孔径微波辐射计接受到的辐射包括水汽和云液态水的辐射信息。水汽和液态水直接影响大气透过率和大气辐射亮温, 从而间接影响辐射计的观测亮

温。为了量化大气参数对辐射计观测亮温的影响, 本节根据场景4和场景5分别计算亮温对水汽含量和云液态水含量的敏感性。

2.2.1 水汽含量敏感性分析

图6为亮温对大气水汽含量在0°～65°范围内的敏感性。从图中可以看出, 水平极化亮温对大气水汽含量的敏感性大于垂直极化亮温。6.9和10.65 GHz对大气水汽含量的敏感性较低, 这表明6.9和10.65 GHz对大气水汽含量反演的影响很小。总的来说, 6.9和10.65 GHz对大气水汽含量的敏感性随着入射角的增大而增大, 其最大值小于0.2 K/mm。

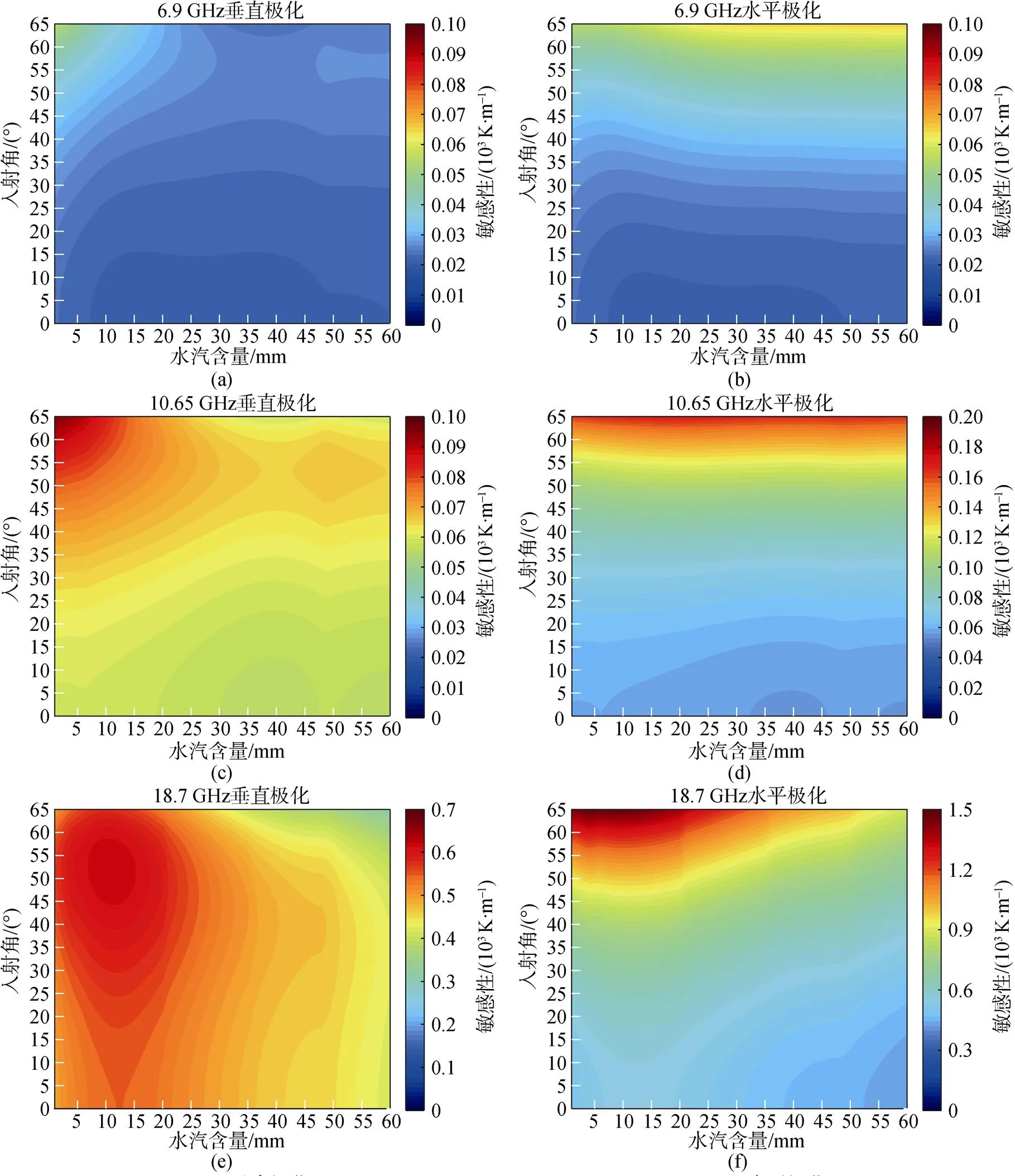
由于23.8 GHz位于水汽的吸收带[29], 其对大气水汽含量的敏感性最大, 所以23.8 GHz是反演大气水汽含量的核心频率。23.8 GHz水平极化亮温对大气水汽含量的敏感性最大值约为4 K/mm (= 1 mm,= 65°)。18.7, 23.8和36.5 GHz对大气水汽含量的敏感性具有相似的特点, 即敏感性随水汽含量和入射角的变化趋势相似。

WindSat提供的大气水汽含量数据是通过18.7, 23.8和36.5 GHz垂直和水平极化亮温反演得到的, 其没有采用6.9和10.65 GHz的原因有两个: (a) 6.9和10.65 GHz对大气水汽含量的敏感性较低, 对提升大气水汽含量的反演精度影响不大; (b) 由于6.9和10.65 GHz的空间分辨率较低, 采用这两个频率进行反演会降低产品的空间分辨率。由于一维综合孔径微波辐射计的空间分率较高, 所以应采用所有频点反演大气水汽含量。从图6可以得出, 18.7, 23.8和36.5 GHz垂直极化亮温对大气水汽含量的敏感性在≤35 mm内较大, 在≥35 mm范围内, 敏感性相对较小。但是其敏感性在0°～65°范围内差别很小。这说明在≤35 mm范围内, 18.7, 23.8和36.5 GHz垂直极化亮温对反演大气水汽含量的影响最大。18.7, 23.8和36.5 GHz水平极化亮温对大气水汽含量的敏感性在≤25 mm和50°≤≤65°范围内较大, 这表明在这个范围内, 18.7, 23.8和36.5 GHz水平极化亮温对反演大气水汽含量的影响较大。

2.2.2 云液态水含量敏感性分析

根据场景5计算了亮温对大气水汽含量在0°～65°范围内的敏感性(图7)。从图7中可以看出亮温对云液态水的敏感性随入射角的增大而增大, 随着液态水含量的增大, 但其变化不明显。6.9, 10.65和18.7 GHz的垂直极化亮温对云液态水的敏感性的最大值没有出现在65°处, 例如图7e中最大值的位置在28°～48°内。23.8和36.5 GHz的垂直极化亮温对云液态水的敏感性随入射角的增大而减小, 水平极化亮温对云液态水的敏感性随入射角的增大而增大。总的来说, 水平极化亮温的敏感性大于垂直极化亮温, 且36.5 GHz对云液态水含量的敏感性最大, 该频点是反演云液态水含量的主要频点。

3 结论

本文提出采用一维综合孔径微波辐射计遥感大气海洋环境参数, 假设该一维综合孔径微波辐射计的观测频率为6.9, 10.65, 18.7, 23.8和36.5 GHz, 并且其入射角在0°～65°之间。本文针对其观测频率和多入射角的特点, 以辐射传输正演模型为基础, 开展了亮温对海面温度, 海面风速, 海面风向, 水汽含量和云液态水含量的敏感性分析。结果如下:

(1) 亮温对海面温度的敏感性: 6.9和10.65 GHz对海面温度的敏感性较高。当入射角一定时, 6.9和10.65 GHz对海面温度的敏感性随海面温度的增加而增加, 但是18.7, 23.8, 36.5 GHz对海面温度的敏感性随海面温度先减小后增加, 说明在相同的亮温测量精度下, 低海温的反演误差大于高海温。当海面温度一定时, 6.9和10.65 GHz的垂直极化亮温对海面温度的敏感性随入射角的增加而增加, 其水平极化亮温对海面温度的敏感性随入射角的增大而减小。18.7, 23.8, 36.5 GHz的垂直极化亮温对海面温度的敏感性与入射角的关系在不同的海面温度范围内表现不同。

(2) 亮温对海面风矢量的敏感性: 水平极化亮温对海面风速的敏感性大于垂直极化亮温, 其中10.65, 18.7和36.5 GHz对海面风速的敏感性较大, 23.8 GHz的敏感性最小。所有频点的亮温对海面风速的敏感性表现相似。在25 m/s≤≤30 m/s范围内, 亮温对海面风速的敏感性随海面风速的增加几乎不变, 这表明在这个范围内风速与亮温呈线性关系。亮温对海面相对风向的敏感性较小, 其最大值均小于0.05 K/(°), 且敏感性随海面相对风向呈波动特征。

(3) 亮温对大气环境要素的敏感性: 水平极化亮温对大气水汽含量的敏感性大于垂直极化亮温。6.9和10.65 GHz对大气水汽含量的敏感性较低, 其最大值小于0.2 K/mm。23.8 GHz对大气水汽含量的敏感性最大, 其水平极化亮温对大气水汽含量的敏感性最大值大约为4 K/mm。18.7, 23.8和36.5 GHz对大气水汽含量的敏感性具有相似的特点。亮温对云液态水的敏感性随入射角的增大而增大, 但是随着液态水含量的增大, 其变化的不明显。36.5 GHz对云液态水含量的敏感性最大, 其水平极化亮温对云液态水的敏感性最大可以达到0.45 K/(0.01 mm)。

致谢: 感谢Wentz提供的海面发射率模型。

[1] YAO P, WAN J, WANG J, et al. Satellite retrieval of hurricane wind speeds using the AMSR2 microwave radiometer[J]. Chinese Journal of Oceanology and Limnology, 2015, 33: 1104-1114.

[2] MEISSNER T, WENTZ F. Ocean retrievals for WindSat: radiative transfer model, algorithm, validation[C]. Proceedings of OCEANS 2005 MTS/IEEE, 2005: 130-133.

[3] LILJEGREN J C, CLOTHIAUX E E, MACE G G, et al. A new retrieval for cloud liquid water path using a ground-based microwave radiometer and measurements of cloud temperature[J]. Journal of Geophysical Research: Atmospheres, 2001, 106(D13): 14485-14500.

[4] BOBYLEV L P, ZABOLOTSKIKH E V, MITNIK L M, et al. Atmospheric water vapor and cloud liquid water retrieval over the arctic ocean using satellite passive microwave sensing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(1): 283-294.

[5] GAISER P, GERMAIN K, TWAROG E, et al. The WindSat spaceborne polarimetric microwave radiometer: sensor description and early orbit performance[J]. Geoscience and Remote Sensing, IEEE Transactions on, 2004, 42: 2347-2361.

[6] WENTZ F J, MEISSNER T. Algorithm Theoretical Basis Document (ATBD) AMSR Ocean Algorithm, Remote Sensing Systems, Santa Rosa, CA, Tech. Rep. 2000, 121599A-1.

[7] SCHANDA E. Multiple wavelength aperture synthesis for passive sensing of the earth’s surface[C]. 1979 Antennas and Propagation Society International Symposium, 1979: 762-763.

[8] RYLEC M. The New Cambridge Radio Telescope[J]. Nature, 1962, 194(4828): 517-518.

[9] RUFC C S, SWIFT C T, TANNER A B, et al. Interferometric synthetic aperture microwave radiometry for the remote sensing of the Earth[J]. IEEE Transactions on Geoscience and Remote Sensing, 1988, 26(5): 597-611.

[10] VINE D M L. The sensitivity of synthetic aperture radiometers for remote sensing applications from space[J]. Radio Science, 1990, 25(4): 441-453.

[11] KILIC L, PRIGENT C, AIRES F, et al. Expected performances of the copernicus imaging microwave radio­meter (CIMR) for an all-weather and high spatial resolution estimation of ocean and sea ice parameters[J]. Journal of Geophysical Research: Oceans, 2018, 123(10): 7564-7580.

[12] WANG Rui, SHI Shunwen, YAN Wei, et al. Sea surface wind retrieval from polarimetric microwave radiometer in typhoon area[J]. Chinese Journal of Geophysics- Chinese Edition, 2014, 57: 738-751.

[13] 陈冠宇, 艾未华, 陆文, 等. 一维综合孔径微波辐射计遥感海面温度的敏感性分析[J]. 海洋学报, 2019, 41(3): 143-154.

CHEN Guanyu, AI Weihua, LU Wen, et al. Sensitivity analysis of remote sensing of sea surface temperature by one dimensional synthetic aperture microwave radiometer[J]. Haiyang Xuebao, 2019, 41(3): 143-154.

[14] MEISSNER T, WENTZ F J. The emissivity of the occean surface between 6 and 90 GHz over a large range of wind speeds and earth incidence angles[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(8): 3004-3026.

[15] MEISSNER T, WENTZ F J. Wind-vector retrievals under rain with passive satellite microwave radiometers[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(9): 3065-3083.

[16] YUEH S H, WILSON W J, LI F K. Modelling of wind direction signals in polarimetric sea surface brightness temperatures[C]. IGARSS’96. 1996 International Geoscience and Remote Sensing Symposium, 1996: 1132- 1134.

[17] GASIEWSKI A J, KUNKEE D B. Polarized microwave emission from water waves[J]. Radio Science $V 29, 1994, 6: 1449-1466.

[18] IRISOV V G. Small-slope expansion for thermal and reflected radiation from a rough surface[J]. Waves in Random Media, 1997, 7(1): 1-10.

[19] MEISSNER T, WENTZ F J. The complex dielectric constant of pure and sea water from microwave satellite observations[J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(9): 1836-1849.

[20] ROSENKRANZ P W. Water vapor microwave continuum absorption: A comparison of measurements and models[J]. Radio Science, 1998, 33(4): 919-928.

[21] LIEBE H J, ROSENKRANZ P W, HUFFORD G A. Atmospheric 60-GHz oxygen spectrum: New laboratory measurements and line parameters[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 1992, 48(5): 629-643.

[22] HOLLINGER J P. Passive microwave measurements of sea surface roughness[J]. IEEE Transactions on Geoscience Electronics, 1971, 9(3): 165-169.

[23] 金梦彤, 刘浩, 武林, 等. 星载一维综合孔径微波辐射计海洋盐度探测任务仿真及外部误差源分析[J]. 遥感技术与应用, 2017, 32(2): 346-355.

JIN Mengtong, LIU Hao, WU Lin, et al. Task simulation and external error sources analysis for an ocean salinity mission with wne-dimensional synthetic aperture micro­wave radiometer[J]. Remote Sensing Technology and Application, 2017, 32(2): 336-355.

[24] 刘泽霖. 综合孔径微波辐射计大气温度廓线直接反演算法[D]. 武汉: 华中科技大学, 2019.

LIU Zelin. An algorithm for retrieving atmospheric temperature profiles directly from visibility function of aperture synthetic microwave radiometer[D].Wuhan: Huazhong University of Science and Technology, 2019.

[25] VORONVICH A G, GASIEWSKI A J, WEBER B L. A fast multistream scattering-based Jacobian for microwave radiance assimilation[J]. IEEE Transactions on Geoscien­ce and Remote Sensing, 2004, 42(8): 1749- 1761.

[26] ALSWEISS S O, JELENAK Z, CHANG P S. Remote sensing of sea surface temperature using AMSR-2 mea­surements[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2017, 10(9): 3948-3954.

[27] GENTEMANN C, WENTZ F, MEARS C, et al. In situ validation of tropical rainfall measuring mission microwave sea surface temperatures[J]. Journal of Geophysical Research, 2004, 109.

[28] GENTEMANN C, MEISSNER T, WENTZ F. Accuracy of satellite sea surfacetemperatures at 7 and 11 GHz[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48: 1009-1018.

[29] LIEBE H J. An updated model for millimeter wave pro­pagation in moist air[J]. Radio Science, 1985, 20: 1069- 1089.

Sensitivity analysis of atmospheric and oceanic environmental parameters based on one-dimensional synthetic aperture microwave radiometer

FENG Meng-yan1, AI Wei-hua1, LIU Mao-hong1, CHEN Guan-yu2, LU Wen1

(1. National University of Defense Technology, College of Meteorology and Oceanography, Nanjing 210000, China; 2. PLA Troop 32033, Haikou 570100, China)

one-dimensional synthetic aperture microwave radiometer; high spatial resolution; multiple incidence angles; sensitivity analysis

Compared with the real-aperture microwave radiometer, the one-dimensional synthetic aperture microwave radiometer has the characteristics of high spatial resolution and multiple incidence angles. This paper proposes a one-dimensional synthetic aperture microwave radiometer operating at observation frequencies 6.9, 10.65, 18.7, 23.8, and 36.5 GHz and an incidence angle range from 0° to 65° to obtain the atmospheric and oceanic environmental parameters. The sensitivity of the polarization brightness temperature to atmospheric and oceanic environmental parameters is evaluated based on the constructed microwave radiation transmission forward model. This research technically supports in determining the key indicators of the radiometer and the retrieval algorithm design. Results show that the sensitivity of the vertical and horizontal polarization brightness temperatures to the environmental parameters shows different characteristics and varies significantly with the incidence angle (0°～65°). The polarization brightness temperature becomes more sensitive to the sea surface temperature at 6.9 and 10.65 GHz, and the sensitivity of the vertical polarization brightness temperatures increases with the incidence angle. The polarization brightness temperature of 10.65 and 18.7 GHz have a relatively large sensitivity to the sea surface wind speed, and The sensitivity is greatest when the wind speed is within 10～20 m/s. The polarization brightness temperature is the most sensitive to atmospheric water vapor content at 23.8 GHz, the sensitivity is large when the water vapor content is low and the incidence angle is large. 36.5 GHz is the most sensitive to cloud liquid water content, and the sensitivity of vertical polarization brightness temperature is opposite to that of horizontal polarization brightness temperature whose sensitivity increases with the incidence angle. In addition, both of them show greater sensitivity when the cloud liquid water content is low.

Jul. 20, 2020

National Natural Science Foundation of China with the grant number, Nos. 41475019, 41705007]

P715.7

A

1000-3096(2021)08-0047-13

10.11759/hykx20200720007

2020-07-20;

2020-12-17

国家自然科学基金 (41475019, 41705007)

冯梦延(1996—), 男, 硕士研究生, 主要从事海洋微波遥感研究, E-mail: a1044175130@163.com; 艾未华(1979—), 通信作者, 博士, 副教授, E-mail: awhzjax@126.com。

(本文编辑: 康亦兼)