复合材料CNG气瓶充气温升的数值模拟

林玉娟，王志伟，高 东

(1.东北石油大学机械科学与工程学院，黑龙江 大庆 163318; 2.中科(广东)炼化有限公司，广州 湛江 524076)

随着压缩天然气汽车的迅速发展，作为其关键零部件之一的压缩天然气气瓶也备受关注。目前，车用的压缩天然气气瓶都朝着轻便化、强压化、高安全性和低成本等趋势发展，因而复合材料CNG气瓶在国内外越来越受到重视。与全金属气瓶相比，复合材料CNG气瓶具有使用寿命较长、强度高、结构轻便、安全性高等优势。但是温度对复合材料有很大的影响，而且复合材料的粘合剂用树脂作为原材料，当出现温度太高的情况时，纤维缠绕层(简称纤维层)与内胆层容易发生脱离，使得容器的负荷能力受到影响，直接影响气瓶的安全使用【1】。天然气气瓶的充装是一个温升过程，为了防止充装过程中气瓶内温度太高，需要研究其快速充装过程，观测快充时的温度变化。此外，天然气加气站在计量天然气时用的是质量流量计，而为了使充装质量达到规定值，气瓶往往充得很满，由于气瓶内的温升作用，充装压力将会上升，这可能致使气瓶的充装压力超出额定值，导致危险发生【2】。因此，对于气瓶的安全快速充装而言，复合材料CNG气瓶的充气温升研究具有实际意义。

国内外已经进行了气瓶快充时温升问题的相关理论与试验研究。Kenneth J Kountz【3】从理论角度对天然气气瓶的快速充装温升问题进行了分析，假设气瓶内部的温度均匀分布，研究结果表明在20 MPa下用5 min将气瓶充满，温升不会高出 30 ℃；Eric Shipley【4】进行的试验研究表明在实际充装时，气瓶温升会略低一些。王恺【5】对复合材料气瓶充放气试验数据和数值模拟数据进行了对比分析，证明了其实际充放气数值模拟模型的真实性。刘伯运【6】为得到充气过程中的温变规律进行了试验与仿真研究，得到仿真结果与试验结果大概相同的结论。以上研究间接表明天然气气瓶温升效应确实存在于气瓶的快充过程，同时也表明了仿真模拟的真实性。

目前，国内外研究学者对于金属内胆CNG气瓶的研究较多，但对于复合材料缠绕的塑料内胆CNG气瓶的充气温升研究很少，因此本文将对全塑气瓶的充气过程进行温升模拟，且将改变气瓶外层传热结构的数值模拟结果与之进行对比，为CNG气瓶的对比研究及优化设计提供一定的参考。

1 理论分析

图1所示的模型为气瓶快充天然气的简化模型，其中A为高压储气罐，B为车载复合材料CNG气瓶。依据模型分析，在复合材料CNG气瓶充气过程中，天然气温升的主要原因有：压缩天然气做功，因此温度升高；在填充时，高压天然气的动能转化为内能，致使温度上升【7】。

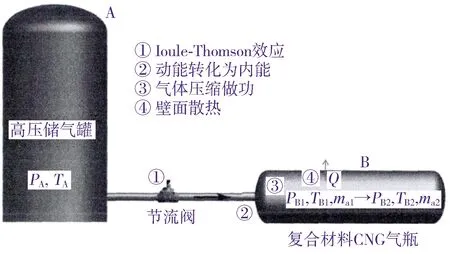
PA、TA分别为高压储气罐中的压力、温度；Q为散热量；PB1、TB1、mB1分别为复合材料CNG气瓶充气前的压力、温度、质量；PB2、TB2、mB2 分别为复合材料CNG气瓶充气后的压力、温度、质量。

由于气瓶实际充装过程中，随着时间的推移，边界层的温度变化较为复杂，热量的传递以热对流和热传导为主，内壁面的传热量随着充气的进行在不断变化，而且内壁传热量对其温度的影响较大，所以用瞬态的数值模拟对气瓶充装过程进行模拟较为合适。

2 数值模型

基于以上情况，本文利用 Fluent17.0 软件对工作压力 30 MPa复合材料CNG气瓶的充气过程进行仿真模拟研究，对不同时间点的气瓶内温度分布与变化以及充气时气瓶的壁面温变状况进行分析；之后在气瓶缠绕层与内胆间加入导热介质，与其进行模拟对比分析。

2.1 数值模拟的基本假设

由于实际模型的繁杂性，气瓶充气的仿真模拟需要进行合理的简化，因此有以下假设：

1)在充气之前，假定储气罐内的温度、气瓶内初始温度、周围环境温度一致；

2)假设气体重力和浮力不计，且在内部气体流动呈轴对称性；

3)假定纤维层为均质性材料，纤维层导热系数为恒定值；

4)假定气瓶壁面与外界空气传热方式为自然对流，则取外壁传热系数为定值；

5)在充气时，假定充装气体基本为甲烷(CH4)气体，天然气中的其他成分不计；

6)假设在充装过程中，储气罐与CNG气瓶连接管道以及节流阀的能量损耗不计。

2.2 控制方程

气瓶充气时的气流实际流场是中强旋流湍流场，湍流具有不可控性，随着时间与空间的改变，流体内的各种物理性质也随之改变。从宏观来看，气体流动倾向于稳态，但并非为稳态，故本文将气瓶充气过程按非稳态处理。Fluent软件是比较强大的求解器，其结合控制方程、湍流模型等可实现对复杂流体流动的数值模拟【8】。

2.2.1 连续性方程

(1)

式中：ρ——密度；

t——时间；

ux、uy、uz——分别为x、y、z方向上速度分量。

2.2.2 动量方程

(2)

式中：p——静压力;

ui——轴向的速度分量;

uj——径向的速度分量；

xi——轴向位移;

xj——径向位移;

Tij——应力张量。

2.2.3 湍流方程

在充气时，压缩天然气气体的流动是湍流，所以湍流模型是否适宜很大程度上影响着模拟结果的准确性。通过对充气时内部气体的流动状况进行分析，认为选用Realizablek-ε模型较为合理【9】。该模型比平板和圆柱射流发散比率模型预测的准确性高。Realizablek-ε模型的表述如下【8】：

湍流耗散率ε和湍动能k的运输方程为：

+Gk+Gb-ρε-YM+Sk

(3)

(4)

式中：μ——垂直于重力的分量；

μt——湍流速率；

σk、σε——分别为k方程和ε方程的湍流Prandtl 数；

Gk——层流产生的湍动能；

Gb——浮力产生的湍动能；

YM——在可压缩湍流中过度的扩散产生的波动；

Sk、Sε——分别为自定义的湍动能项和湍流耗散源项；

C1、C1ε、C2、C3ε——常量；

ν——流体平行于重力的速度分量。

在Fluent中默认值为C1=1,C1ε=1.44，C2=1.9，C3ε=1.0，σk=1.0，σε=1.2。

2.2.4 能量方程

(5)

式中：E——气体能量；

keff——有效热导率；

Cp——定压比热容；

Prt——湍流的普朗特数；

T——温度；

(τij)eff——偏应力张量。

2.2.5 真实气体方程

由于气体温度升高的最主要原因是气体压缩做功，气体分子间作用力对气体与内壁面强对流传热有影响，因此，30 MPa压力下充装时内部高压气体也不能被看作理想气体，为模拟充装时的气体热力状态，必须采用一种真实气体模型。本文采用真实气体Redlich-kwong方程，详细表述如下【10】：

(6)

式中：R——普适气体常量；

νm——摩尔体积,νm=1/ρ；

a、b——两个物理常数。

其中a和b的表达式为：

(7)

(8)

式中：Tc——甲烷的临界温度；

Tc——甲烷的临界压力。

2.3 壁面材料属性

采用80L、30 MPa的工况进行快速充装温升分析，其壁面各层材料属性如表1所示。

表1 气瓶壁面材料物性参数

2.4 求解相关设置

气瓶选择压力为基础的求解器，具体为耦合式求解器(PBCS)，即同时求解压力和动量方程。充气过程由于气瓶内部气体随着时间变化，故采用瞬态求解，选择压力入口边界，且随时间线性变大。用UDF编译其入口条件，方程为:

Pin=2 000 000+233 333.333·t

(9)

式中：Pin——入口压力。

由于气瓶充装前其内部均会有残余压力，故本文中气瓶初始压力设为2 MPa，起始温度293 K，加注速率为66.7 g/s，2 min充装完毕，终止压力30 MPa。气体方程选择为真实气体方程，湍流模型选择为Realizablek-ε模型，由于充气过程涉及传热，故开启能量方程。

3 结果与分析

3.1 气瓶温度场模拟结果与分析

图2～图4分别展示了气瓶在充气到10 s、30 s、120 s时的温度云图。由图2～图4看出：在充气过程中气瓶瓶尾的封头段小块区域基本分布了高温区域，而气瓶的进口位置则分布了低温区，进口处的温度分布呈现羽流状；在充气前期(t=10 s)，气瓶进口温度比内部最高温度低42 K，且前期内部气体温度上升的速率快；气瓶充气30 s时，最高温度区域面积减小，气瓶内温度分布层次更加分明，但高温区保持不变；充气结束(t=120 s)时，内部气体的温度分布状况与30 s时基本一致，由此可知，在充气后期气体基本稳定流动。

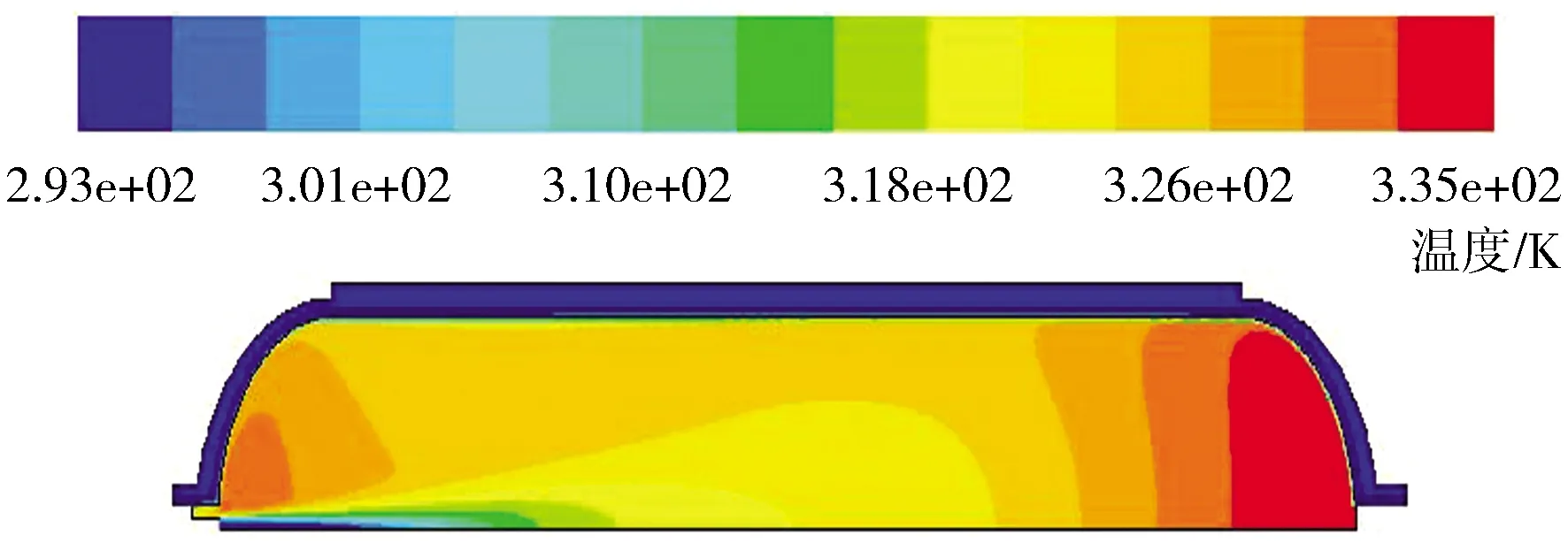
图2 10 s时的温度云图

图3 30 s时的温度云图

图4 120 s时的温度云图

图5展示了内部气体在充装过程中的最高温升和平均温升。由图5可以看出：随着充装时间的增长，内部气体温度持续升高，但是与时间成非线性关系；气瓶加注时的前20 s，气瓶内气体的温升速率偏快，最高温度与平均温度分别比充气前上升了约52 K和40 K。

图5 充装过程内部气体平均温度和最高温度变化曲线

从加注时间20 s至加注结束时的120 s，内部气体的温升速率快速降低，最高温度与平均温度分别比充气20 s时上升了6.14 K和5.25 K。以上现象表明，充气初期合理地控制的充装速率可以使气瓶内部温度有一定幅度的下降。

在加注过程中，气体动能转化为内能和气瓶压缩做功是气瓶内部温升的主要因素。在充气初期，气瓶内压与外界压力相差较大，气体充装速率快，因此充气初期气瓶内部温升速率快。在充气后期，气瓶内压与外界压力差逐渐变小，使得气体的加注速率变慢，并且气瓶内温度极高，热量大部分都通过壁面扩散到外界环境当中，所以充气末期气瓶内部温升速率较慢。

3.2 气瓶壁面温升的分析

在气瓶加注过程中，按照相关规定，气瓶壁面的许用温度为80 ℃。因为气瓶壁面的主要结构是玻璃纤维缠绕层和内胆层，若壁面温度太高，纤维层的强度和使用寿命势必会受到影响，从而使复合材料气瓶使用的危险性提高。因此在模拟过程中，在气瓶纤维缠绕层与内胆层的交界面选取了4个点，对壁面温升状况进行监测。图6为选取的壁面监控点位置示意。

图6 气瓶壁面监控点位置示意

图7是监控点在加注过程中的温升曲线。由图7中的曲线可知，在充气结束时,其瓶尾段壁面温度最高，但在充气初期，气瓶筒身中段壁面的温升速率比瓶尾处壁面的温升速率高。监控点2(0.5,0.166)与监控点3(0.75,0.166)位于气瓶筒身中段(监控点坐标单位为m)，且两点位置都处于气瓶回旋流的区域，在充气的初期，加注速率高，气流回旋与壁面摩擦，产生了强制对流现象，所以气瓶筒身中段壁面的温升速率快。在充装时，内部气体受到压缩，密度上升，导致其流动速率变小，从而使得强制对流产生的热量变少，进而引起筒身中段壁面的温升速率降低。监控点4(0.95,0.166)位于瓶尾，这一监控点气体流速极小，接近于零，故瓶尾处的对流可以看作是自然对流，因此充装初期气瓶筒身中段的温升速率高于瓶尾的温升速率。随着加注过程的进行，气体高温区一直分布于气瓶的尾部，且内部气体温度不断升高，瓶尾部分内外的温差持续加大，导致传热速率也在持续升高，致使充气结束时在瓶尾区域出现壁面温度的峰值。

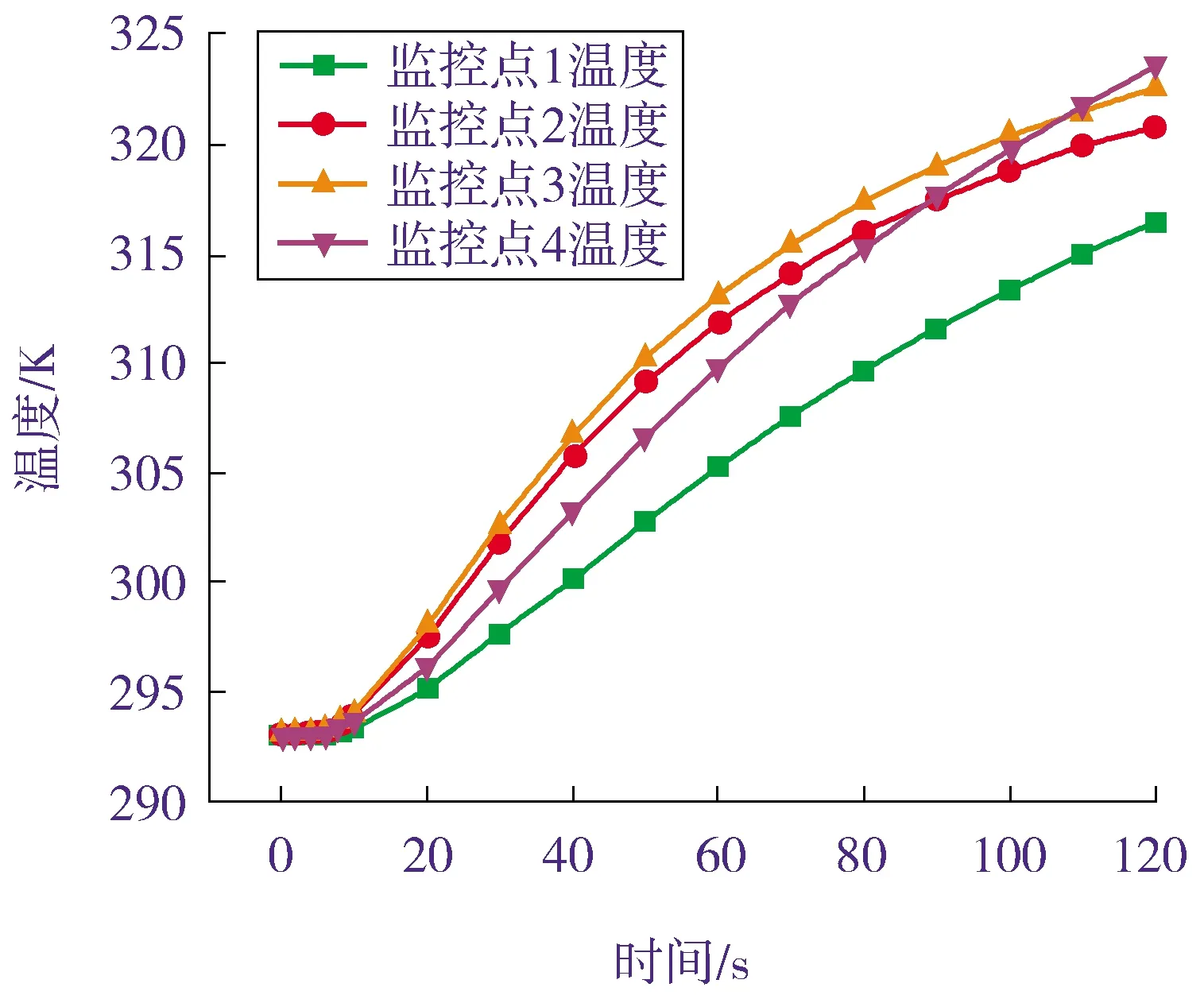
图7 气瓶壁面监控点温升曲线

气瓶纤维缠绕层与内胆层在充气时的平均温升和最高温升曲线如图8所示。从图8的曲线可以看出：气瓶的壁面温升和充气时间成非线性关系；充气结束后，纤维缠绕层与内胆层的最高温度没有超过气瓶的许用温度80 ℃(353.15 K)；在充气前期，纤维缠绕层的温升速率较低，随着充气的进行，其温升速率提高，但最高温升与平均温升相差较大，内胆层的温升速率有所下降。

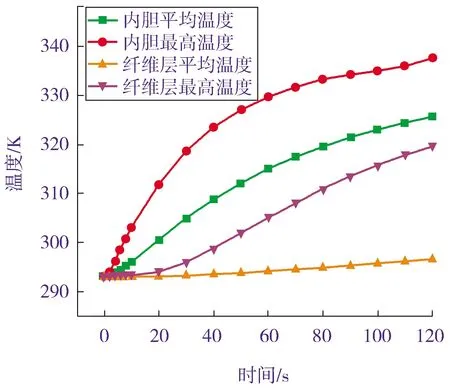
图8 气瓶壁面平均温升和最高温升曲线

从图8中还可看出：纤维缠绕层的最高温升速率与平均温升速率相差较大。由此可知，纤维缠绕层温度呈现不均匀分布，这是由于复合材料层偏低的热传导率导致的。随着充气的进行，气体密度逐渐变大，流速随之下降，因此对流系数变小，进而使得气体温升速率降低。气体温升速率急速下降也导致了内胆层温升速率的下降。

3.3 导热胶泥的应用

因为空气的导热系数极低，导致气瓶无法通过热传导迅速把热量扩散出去，气瓶中的热量传递只能是被通过密封于内胆与纤维层间空气的对流传热实现，所以会出现以下情况：

1)传热效果差，易使内胆出现缺陷。由于气瓶中的热量不易散发到空气中，因此内胆的温度可能达不到所要求的水平，这就可能会使内胆长时间受热，严重时会导致其出现缺陷。

2)传热效果差，易使内胆与纤维缠绕层之间产生分层现象。气瓶的内胆层与纤维缠绕层是贴紧但分离的一个状态，纤维层的内壁依附于内胆层上，二者之间几乎没有粘合力。

3)受热面不均匀，易使结构改变。由于热量在瓶内的不均匀分布，导致结构各部位的受热程度不同，使得气瓶各部位变形量不同，如果长时间积累，可能导致结构形状产生大的改变。

解决普通散热问题可采用导热胶泥。导热胶泥俗称导热泥或导热凝胶，是以硅胶为基体，填充以多种高性能陶瓷粉末制成的类似于橡皮泥状的一种导热黏土。导热胶泥具有导热率高、可压缩性强、可塑性高、抗老化、耐高温、耐辐射、绝缘等优良性能，并且在-50 ℃～200 ℃的温度下可长时期保持膏状。将其放置于内胆与纤维缠绕层之间的空隙处，使导热胶泥层代替原来的空气层，可在很大程度上扩大内胆与纤维缠绕层间的传热面积，同时使传热方式由原来的热辐射变为热传导。高导热系数的导热胶泥可以将气瓶中的热量迅速传到外界环境中，从而提升内胆与纤维缠绕层间的传热效率，确保散热要求。导热胶泥的使用对气瓶的安全快速充装具有实用价值。

依据对气瓶壁面温升状况的分析，纤维缠绕层与内胆层的最高温度虽然均没有超过气瓶的许用温度80 ℃(353.15 K)，但是内胆层的最高温度已经与许用温度十分接近，为了使气瓶的安全性更高，需在气瓶的壁面中加入导热胶泥，加速壁面传热。本次模拟采用JM-250有机型导热胶泥，其对金属和非金属具有较强的附着力。由于导热胶泥的粘接强度较高，由导热胶泥与金属和非金属之间的线膨胀系数不同而产生的温差应力足以被导热胶泥与其之间的结合力克服，因此仅需将导热胶泥涂抹在内胆与纤维缠绕层之间即可。涂抹效果如图9所示。

图9 加入导热胶泥后气瓶简化的几何模型

设置同样的模拟条件，并将导热胶泥的导热系数设置为10.5 W/(m·K)。对加入导热胶泥后的气瓶再次进行充气模拟，在气瓶壁面选取同样的监控点对充气过程中壁面温升情况进行监控。通过监测得到了新的监测点温升曲线和壁面温升曲线。

图10为加入导热胶泥后的监控点温升曲线。从图10中可以看出：4个监控点的整体温升速率有所降低，可能是有导热胶泥层之后,散热速率加快，导致了监控点的温升速率变慢；并且图中监控点位置的最高温度均低于未加导热胶泥层时，这表明导热胶泥对扩散气瓶快速充装时产生的热量起到了一定的促进作用。

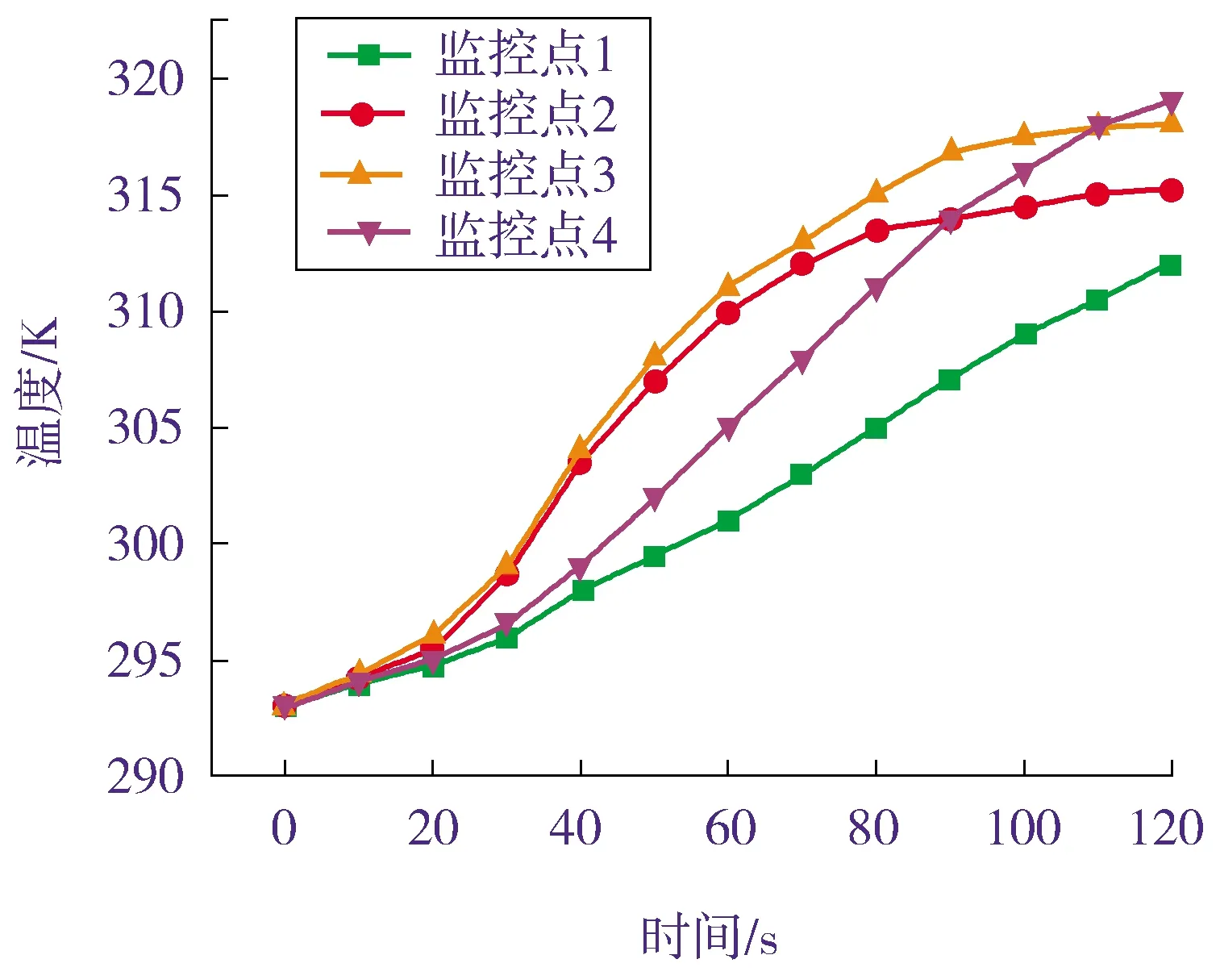
图10 加入导热胶泥后壁面监控点温升曲线

图11为加入导热胶泥后壁面平均和最高温升曲线。从图中11可知：在充气后期，内胆层温升速率较之前有所上升，并且在充气过程中温升速率变化不大。纤维层平均温升速率与最高温升速率基本一致，且较之前平均温升与最高温升的差值变小；充气结束时，内胆层与纤维层的平均温度和最高温度均较之前有所下降。在充气过程中，内胆层温升速率较为稳定，这是因为加了导热胶泥后，气瓶的散热速率增大，充气前期导热胶泥层快速扩散掉了内胆层的高温，使内胆层温度升高不明显，温升速率一直保持稳定，所以在充气后期其温升速率较之前有所升高。加入导热胶泥后，复合材料层的热导率升高，使得纤维层的平均温升与最高温升差值变小，且由于温度扩散加快，在充气结束时，纤维层平均与最高温度均有所降低。

导热胶泥层的加入使得内胆层最高温度较之前有所下降，一定程度上增加了气瓶充装的安全性，也使得纤维层温度升高速率较为稳定、纤维层与导热胶泥层不会因为温差过大而发生剥离，从而延长气瓶的使用寿命。

3.4 模拟可靠性验证

对文献【11】中的试验气瓶进行充氢模拟，并与文献试验进行对比，以验证模拟的正确性和可靠性。该文献中的试验高压氢气瓶为Ⅲ型气瓶，容积为74L。建立与本文模型相同假设的模型，其起充压力为9.43 MPa，终止压力为35 MPa，充气时长38 s，选择压力入口边界，并且为更加贴合文献试验，选择压力拟合曲线，用UDF方程编译，即

Pin=-11 800t2+1 117 200t+9 380 500

(10)

仿真模拟与试验进口压力对比如图12所示,仿真模拟与试验的平均温升对比如图13所示。由图13可见，气瓶平均温度随着时间的推移逐步上升，上升速率逐渐缓和，且仿真模拟结果与试验结果趋势相符，得到的结论相同，最大误差6 K，在允许范围内。上述结果表明，本文的气瓶充气温升数值模拟较为准确。

图13 仿真模拟与试验的平均温升对比

4 结论

为对气瓶快充温升现象进行分析，对工作压力为30 MPa的复合材料CNG气瓶建立了快充过程的仿真模型，并对其进行研究，研究结果如下：

1)在充装的整个过程中，气瓶瓶尾的封头段基本分布了高温区域，而进口位置则分布了低温区，进口处的温度分布呈现羽流状；

2)气瓶内部气体温度随着充装的进行在持续上升，但是与时间不成线性关系；

3)在充气前期，纤维层的平均温升和最高温升速率较低，随着充气进行，纤维层最高温升的速率有明显提高，而纤维层平均温升的速率提升幅度较低，同时，内胆层的温升速率小幅降低；

4)气瓶的壁面温升和充气时间成非线性关系；

5)加入导热胶泥层之后，内胆层与纤维层的平均温升速率与最高温升速率都保持相对稳定，且在充气结束时平均温度与最高温度均较之前有所降低。