龙卷风涡旋场气流的动力学分析

武 圆

(北京人文大学，北京 101300)

引 言

龙卷风一般持续时间短，袭击时间突然，破坏力强，常给人民的生命财产带来巨大损失[1-5]。虽然有学者在17世纪就对龙卷风开始了研究[6]，但直到目前关于龙卷风的问题依然是世界难题[7-8]。目前国内也有学者对龙卷风的涡旋结构与维持特性进行了理论研究与讨论[9-12]，但更多的学者则倾向使用数值模拟来研究探索龙卷风涡旋场[13-18]。由于人们对龙卷风涡流场缺乏足够的认识与了解，以至于在对处于龙卷风涡旋场中的物体进行受力分析时缺乏必要的可靠理论依据。比如现行的二维Rankin平面涡旋模型就没有考虑龙卷风涡旋对物体的轴向作用力，而一些三维龙卷风涡旋模型如Wen建立的半经验三维理论风场模型对气压降考虑得不够完善，Burgers三维龙卷风涡旋模型对龙卷风轴向运动气流的描述与实际情况不一致，而其他的一些三维龙卷风涡旋模型也都与现实风场存在一定的差距[19]。对此，本文将根据新提出的龙卷等涡旋的动力学模型[20]，分别对龙卷风涡旋场中旋转与轴向运动气流的运动与受力,以及物体在龙卷风涡旋场中径向与轴向的受力，进行理论分析，以期使人们对龙卷风的涡旋现象有更深刻的认识与理解，并为学者在以后研究龙卷风等涡旋方面的问题[21-25]时提供必要可靠的动力学模型和理论计算方法。比如依据本文对龙卷风涡旋动力学的分析与理解，可进一步研究解决一般中气旋形成龙卷风的理论判据，或一般龙卷风的生成条件，以在对龙卷风预警时可以提前更多的时间并提高预报精度，甚至在未来有可能将龙卷风灾害消灭在生成阶段，可以最大限度地将龙卷风灾害影响降到最小。

1 龙卷风涡旋动力学模型及其涡旋场负压差计算

1.1 龙卷风涡旋的动力学模型及其压差变化梯度场的计算

龙卷风涡旋运动涡核区的气流属于以一定角速度ω进行涡旋运动的层流，其涡核区的涡旋运动气流的压差分布可依据龙卷风快速旋转的气流所具有的离心力Fa与旋转气压梯度力Fp平衡的物理条件得出[20]。如图1所示，其中，r为旋转气流位置到旋转中心的距离，Δr为旋转气流层的厚度；Δz为旋转气流层动力学模型的高度，并取Δz充分小；ω为龙卷风风场旋转气流的角速度；ρ为旋转气流的密度。根据龙卷风涡旋风场的旋转气流层动力学模型，可得在龙卷风涡核区中的压差p的变化梯度随涡旋半径的变化规律。

图1 龙卷风涡旋风场r处旋转气流层的动力学模型

若取Δr→0，则涡旋气流层在位置区间[r，r+Δr]处的质量Δm=2πr·Δr·Δz·ρ，旋转气流速度v=rω，且旋转气流层在位置区间[r，r+Δr]处承受的负压强差为Δp(r)，则承受负压强差为Δp(r)的面Δs(r)=2πr·Δz，则根据Fa=Fp：

(1)

(2)

令Δr→0，则由式(2)可得：

(3)

式(3)表示的是在龙卷风的涡旋场内压差变化梯度随其半径的变化关系。

1.2 龙卷风涡旋场中涡旋气流承受的负压差的计算

由式(3)可知，龙卷风压差梯度场中r位置涡旋气流承受的相对大气常压的负压差p(r)：

(4)

2 一般几何形物体在龙卷风梯度场径向的受力分析

根据龙卷风动力学模型及该模型的压差变化的梯度场方程式(3)，假设在该龙卷风的动力学模型中存在一物体Ω=Ω(x,y,z)，其中Ω(x,y,z)为该物体的体函数,且该物体完全存在于龙卷风涡旋梯度场内，则在该物体中任取一点Ω(xi,yi,zi)，以及该点的无限接近点Ω(xi+Δx,yi+Δy,zi+Δz)，则以该两点为对角点组成了一个边长分别为Δx、Δy和Δz的矩形(如图2)。其中rmin与rmax分别为龙卷风旋转气流的内外边界。

图2 物体在龙卷风梯度场的受力分析

显然，该体元的体积ΔΩ=Δx·Δy·Δz。由龙卷风的动力学模型可知：该体元ΔΩ沿水平方向(坐标x轴和y轴方向)承受梯度压强差，令该体元承受沿x轴方向上的梯度压强差为Δp(xi)，y轴方向上的梯度压强差为Δp(yi)，z轴方向上的梯度压强差为Δp(zi)，且龙卷风涡旋场铅垂面上没有旋转气流存在，所以z轴方向上的梯度压强差Δp(zi)=0。

结合式(3)，若令Δx→0，可得该矩形承受x轴方向上的梯度压强差为Δp(xi)：

(5)

对于该矩形ΔΩ，承受该梯度压强差Δp(xi)的面定义为：ΔSyz=Δy·Δz，则该矩形承受的沿x轴方向上的梯度压差力为ΔF(xi)，该力指向涡旋中心，且令Δx→0、Δy→0、Δz→0，则：

ΔF(xi)=Δp(xi)·ΔSyz=ρω2xi·ΔΩ

(6)

当式(6)中ΔF(xi)的xi取值遍历其所占体积Ω(x,y,z)的取值范围，可得在该龙卷风的动力学模型中一个其体积为Ω物体的所承受的沿x轴方向上的压差力F(x)：

(7)

对比式(7)可得该物体承受的沿y轴方向上的压差力F(y)，同理该力指向涡旋中心，且

F(y)=∭Ωρω2y·dΩ

(8)

于是可得该体积为Ω的物体在龙卷风中受到的径向合力F(r)：

(9)

以上分析与计算为一般物体在龙卷风的压差梯度场的径向受力分析过程与计算方法。式(7)(8)与式(9)表明，物体在龙卷风涡旋场中受到的径向力等于该物体在龙卷风涡旋压差梯度场的体积分，即气压梯度力对处于龙卷风涡旋场中物体的作用及表现形式。

3 龙卷风涡旋场轴向运动气流的动力学分析

3.1 龙卷风涡旋场对接触地面(或大气)的作用力分析与计算

当龙卷风涡旋场两端的负压区暴露时，或者龙卷风涡旋场的底部接触地面或大气时，龙卷风涡旋场与地面(或大气)存在接触面。此时分析龙卷风涡旋场对接触面的作用力。由图2可知，龙卷风涡旋底部与地面(或大气)的接触面为旋转气流的内外边界rmin与rmax所围成的环面，且令该环面为D(0)，0为龙卷风涡旋距离地面高度为0的接触环面。

在龙卷风涡旋场与地面接触的面上任取一点D(xi,yi,0)及该点的无限接近点D′(xi+Δx,yi+Δy,Δz)，并组成涡旋场气流体元，且在该点D(xi,yi,0)气流体元与地面接触，并结合式(4)可得，在龙卷风旋转气流涡旋场中，在D(xi,yi,0)位置点上涡旋场气流体元存在一个相对于大气压的压差p(xi,yi,0)，则

(10)

则已知点D(xi,yi,0)与该点的无限接近点D′(xi+Δx,yi+Δy,zi+Δz)所构成的气流体元ΔΩ=Δx·Δy·Δz的底部与地面接触，根据压差各向同性的原理，可以得出地面在涡旋场D(xi,yi,0)处也存在相对大气压的负压差p(xi,yi,0)，且该处与体元接触的地面在压差p(xi,yi,0)的作用下沿涡旋轴向的受力为ΔFi(0)，且同时令Δx→0、Δy→0，则：

ΔFi(0)=p(xi,yi,0)·ΔxΔy

(11)

结合式(10)，当式(11)中xi、yi的取值遍历龙卷风涡旋底部与地面的接触面D(0)的取值范围，可得龙卷风涡旋场对接触地面D(0)的轴向作用力F(0)：

(12)

由于龙卷风涡旋底部与地面(或大气)的接触面为旋转气流的内外边界rmin与rmax所围成的环面，则式(12)中

并直接计算式(12)，得F(0)：

(13)

分析式(13)的结果可知，当涡旋气流与地面接触形成龙卷风时，其旋转气流层将与地面接触，而此时龙卷风涡旋底部气流层存在的相对于大气压的压差p(x,y,0)将会与地面产生作用，并对地面产生一个沿涡旋场轴向的压强吸力，该吸力将把龙卷风涡旋气流经过地方的气流、泥土、甚至树木脱离地面，式(13)的计算结果即该吸力的值。

3.2 龙卷风风场内轴向运动气流的受力分析

根据上文3.1章节的分析可知，当环境中的气流体元通过涡旋气流与地面(或大气)的接触面在压差p(x,y,0)作用下而进入龙卷风涡旋场并沿涡旋场轴向运动，并同时在涡旋场中与作旋转运动的涡旋场气流形成螺旋向上复合运动的涡旋气流，且当该轴向运动气流体元形成螺旋向上复合运动的涡旋气流后，则根据式(3)(4)(5)的分析可知,该进入龙卷风涡旋场中气流体元也会因其具有旋转运动而在该涡旋场中继续产生压差，即当气流体元在龙卷风涡旋场中沿轴向运动一定距离Δz后，该轴向运动的气流体元也会因其旋转运动而在其螺旋上升的同时在该涡旋场D(x,y,0)处产生压差p(x,y,0)，且使后续在涡旋场底部的气流体元也处在压差p(x,y,0)的作用下而被持续地吸入龙卷风涡旋场中。

假设当环境中的气流体元通过涡旋气流与地面(或大气)的接触面进入龙卷风涡旋场中运动一定距离Δz后不再作轴向运动而仅作涡旋旋转运动时，则后续在轴向压差p(x,y,0)作用下而作上升运动的气流体元以一定的速度动能(见式(17)的分析，负压差对气流体元的做功完全转化为体元的动能，两者完全相等)接触于该体元的底部面元时，后续上升的气流体元所具有的动能转化为对该体元的底部面元的正压强能，进而把该气流体元在上升一定距离Δz后底部所受到旋转气流层产生的负压作用平衡掉，使该体元的底部不再承受负压差。即该上升一定距离Δz后的气流体元的底部相当于受到的压强为大气常压，而该气流体元的上部面元仍会继续受到旋转气流层产生的轴向负压差作用，则使该气流体元在龙卷风涡旋场中上升一定距离Δz后仍会在轴向压差作用力下继续沿其轴向运动。

若对在龙卷风涡旋场中轴向运动的气流连续分析可知,气流体元在涡旋场轴向运动过程中,始终承受涡旋旋转气流产生的轴向压差作用，这与其在涡旋场轴向运动的高度无关，仅与从涡旋底部是否有连续进入涡旋场的气流有关。这也是一般常见的龙卷风涡旋中的气流总是螺旋连续上升的原因。也即当龙卷风涡旋底部有连续进入涡旋场的气流并上升一定高度z时，则该连续进入涡旋场的气流在涡旋轴向运动上仍会受到轴向压差p(x,y,z)的作用，其中p(x,y,z)为在龙卷风涡旋场中(x,y,z)高度位置中存在的相对于大气常压的压差值。

3.3 龙卷风涡旋场轴向运动气流的速度分析与计算

根据功能守恒定律，针对体元可得ΔW=ΔEk+ΔEp，

即

(14)

化简：

(15)

式(15)的计算结果为高度z上点D(x,y,z)处轴向压差p(x,y,z)对气流体元ΔΩ的做功，所以取其运动高度Δz→0，则式中ρ(z)gΔz项为一阶无穷小项，予以忽略。则式(15)化为

(16)

带入式(10)，可得体元在压差p(x,y,z)作用下的气流轴向运动瞬时速度：

(17)

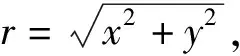
在龙卷风涡旋场中，虽然在高度方向上不存在因旋转气流存在而产生的梯度压差，但是进入涡旋场中沿轴向运动的气流，都会在轴向压差p(x,y,z)的作用下，不断以一瞬时速度v(x,y,z)沿龙卷风轴向运动。比如对于水龙卷而言，其涡旋场中存在的最大的压差仅为一个大气压，一般一个大气压的压差最多能使水抬升10 m左右的高度，但在水龙卷中，则能使水以一定速度被抬升上千米高度。

式(15)中的一阶无穷小项ρ(z)gΔz也体现了龙卷风对进入其涡旋场的气流(以及水流或其他物质)一直做功的方式，虽然在龙卷风涡旋场每点高度上其轴向压差p(x,y,z)对轴向运动气流克服重力做功几乎为零，但这却是龙卷风本身能量的一种耗散方式，也是龙卷风涡旋存在周期短的重要原因之一。

根据式(17)可知，龙卷风在接触地面或水面的瞬间，会吸入尘土或水，使其轴向运动气流的密度大于龙卷的水平旋转气流的密度，其龙卷涡旋气流的旋转速度会大于其轴向瞬时速度。但当龙卷风在接触地面或水面一段时间后，其轴向运动气流的密度会与龙卷的水平旋转气流的密度相等，龙卷涡旋气流的旋转速度也会与其轴向瞬时速度相等。

4 一般几何形物体在龙卷风涡旋场轴向的受力分析与计算

假设在一存在连续轴向运动气流的龙卷风涡旋场内存在一物体，且根据上文3.2与3.3章节的分析可知，该物体的底部存在连续轴向运动的气流，则该物体的底部在后续轴向上升气流动压的作用下，该物体底部受到旋转气流层产生的负压作用被平衡，受到的压强为大气常压。且由于涡旋气流压差的各向同性的特点，则该物体的上表面会受到涡旋场中旋转气流产生的相对于大气常压的负压差的作用，使该物体在涡旋场中承受轴向压差，并沿轴向受力。图3为物体在龙卷风涡旋场的轴向受力示意图。

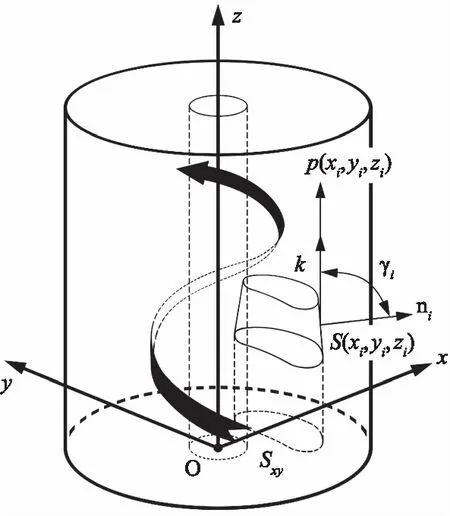
图3 物体在龙卷风涡旋场的轴向受力示意图

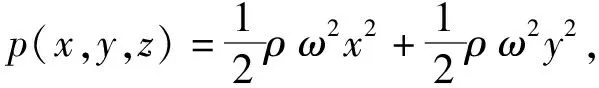
ΔF(zi)=p(xi,yi,zi)ΔSicosγi

(18)

根据高等数学中关于面积分的分析，当式(18)中ΔSi的取值遍历该物体的表面方程S=S(x,y,z)的上表面时，取面元ΔSi→0时，可得该物体Ω=Ω(x,y,z)在龙卷风涡旋场所受到的轴向合力F(z)：

(19)

式(19)即为该物体Ω=Ω(x,y,z)在龙卷风涡旋场中轴向受力的合力F(z)及其计算方法，其中Sxy为该物体的上表面方程S=S(x,y,z)在龙卷风涡旋场中x—o—y平面上的投影。

5 龙卷风涡旋场内边界(风眼)成因分析

5.1 龙卷风上升气流在其涡旋平面上的物质通量分析与计算

根据式(17)可知，在龙卷风涡旋场内，沿轴向运动气流高度z上的瞬时速度v(x,y,z)与其到涡旋中心的距离r不等而不同。假设，若该龙卷风涡旋稳衡存在，则该龙卷风在高度方向上旋转角速度ω相等，且令龙卷风涡旋场中的沿轴向运动的气流密度与旋转运动的气流密度ρ相等，则根据式(17)，可得沿轴向运动气流高度z上的瞬时速度v(x,y,z)=rω，即涡旋场的上升速度与其旋转速度相等,即涡旋气流层在位置区间[r，r+Δr]处Δt时间内的沿轴向运动的物质通量QΔt(r)：

QΔt(r)=2πrΔr·rω·Δtρ

(20)

取Δr→0，可得在龙卷风涡旋z高度平面D(z)上在时间Δt内沿轴向运动的物质通量QΔt：

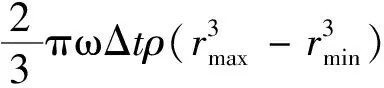
(21)

则单位时间内通过龙卷风涡旋z高度平面上的物质通量Q=QΔt/Δt，即

(22)

该龙卷风涡旋z高度平面上的物质通量Q可以估算龙卷风涡旋场对沿轴向运动物质的运输效率。

5.2 龙卷风涡旋场内边界rmin成因分析

下面根据物质通量的守恒原理，对龙卷风内边界rmin给出其存在机制原理，并给出其存在的条件。在龙卷风轴向上任取两个与其轴向垂直的两个面D(z1)与D(z2)，其中z1与z2分别表示龙卷风在不同高度位置的环面(龙卷风涡旋气流在不同高度上内外边界rmin、rmax组成的环面，见图2)，且z2>z1，并根据一般龙卷风在实际存在中一般为“漏斗”状，即D(z2)高度位置的涡旋外边界半径rz2max一般大于或等于D(z1)高度位置的涡旋外部边界半径rz1max，则令：rz2max=λrz1max，其中λ≥1。且根据式(17)，假设在该龙卷风涡旋场内，流经面D(z1)与D(z2)气流的密度分别为ρ(z1)、ρ(z2)，即在同一涡旋面上，旋转与轴向运动气流的密度均相等。且令龙卷风涡旋场在D(z1)面的内边界rz1min=0，龙卷风在高度范围内其旋转角速度均不变，为ω。则根据式(22)，可得龙卷风涡旋场在D(z1)面沿轴向运动气流的物质通量Q(z1)：

(23)

同理依据式(22)可得龙卷风涡旋场在D(z2)面沿轴向运动气流的物质通量Q(z2)：

(24)

根据物质通量的守恒原理，可得龙卷风涡旋场在D(z1)面沿轴向运动气流的物质通量Q(z1)与其涡旋场在D(z2)面沿轴向运动气流的物质通量Q(z2)必然相等，即Q(z1)=Q(z2)。于是联立式(23)与式(24)，并移项化简可得

(25)

式(25)即是龙卷风涡旋场内部边界存在的决定式。根据式(25)可知，若流经面D(z1)与D(z2)的气流密度满足关系λ3ρ(z2)=ρ(z1)，则龙卷风涡旋场在面D(z2)位置上不会存在一个边界为rz2min的区域；同理，若λ3ρ(z2)-ρ(z1)>0，则龙卷风涡旋场在面D(z2)位置上一定会产生一个不为零的边界区域rz2min。由以上分析可知，龙卷风内部边界rmin是由物质通量的守恒原理的限制产生的。

6 结论与应用展望

6.1 结 论

(1)根据龙卷风场的动力学模型，以及由该动力学模型得出的龙卷风涡旋压差变化梯度场gradp(r)=ρω2r·er，进一步研究分析得出一般物体在龙卷风梯度场中所承受的径向力即等于该物体在该梯度场中的体积分；并依据龙卷风涡旋场的压差变化梯度场，计算出涡旋气流承受的相对于周围大气压的负压差的分布规律(式4)；依据式(4)，并结合理想流体中压差的各向同性的特性，对龙卷风涡旋场中的气流在轴向上的受力与运动进行了理论分析，并得出其气流的轴向运动是由其涡旋场中水平旋转气流运动影响产生的，涡旋气流的水平运动与轴向运动是不可独立对待、分析的。这也是文中关于龙卷风涡旋动力学模型中，仅设定存在龙卷风涡旋气流的水平旋转运动，却依然可分析其涡旋气流的轴向运动的原因。通过对物体在龙卷风涡旋场轴向的受力分析与研究，得到物体的轴向受力表达式式(19)。

(2)论文依据对龙卷风涡旋场中轴向运动气流的分析，对龙卷风轴向运动气流的物质通量进行了分析与计算，并给出龙卷风内部边界rmin(或风眼)的存在需要满足式(25)要求的条件：λ3ρ(z2)-ρ(z1)>0，即该风眼产生的原因是龙卷风轴向运动气流遵守物质通量守恒的结果。

6.2 应用展望

文中依据新的龙卷风涡旋的动力学模型，分析得出的物体在龙卷风涡旋场中的径向与轴向受力计算表达式，以及相关的分析过程与计算方法，都具有重要的应用意义，可以预见的有以下三个方面的应用：

(1)建筑风工程理论研究方面。比如对国家核电站等重要或其他安全等级要求较高的建筑设施，需要考虑对龙卷风涡旋的受力校核，那就可以根据该文章所得出的式(7)(8)(9)与式(19)分别对处于龙卷风涡旋场的设施与建筑物沿涡旋径向与轴向受力进行理论分析与计算。

(2)龙卷风的数值模拟与有限元分析方面。如果现实中的一些物体(比如一些桥梁和铁塔)是异形的，难以在龙卷风涡旋场中对物体的外形Ω=Ω(x,y,z)及其在涡旋轴向投影Sxy进行参数化方程建模，也即无法直接应用文中式(7)(8)(9)与式(19)对处于涡旋场中的物体进行受力计算。这时就需要对物体进行三维仿真建模，并同时通过流体有限元分析软件，对龙卷风涡旋场进行参数化定义与描述，并通过本文对物体在龙卷风涡旋场中的受力分析方法，将文中关于物体的线元、面元与体元按精度要求具体赋值，也即将物体在龙卷风涡旋场中进行网格参数化，进而对物体在龙卷风涡旋场中的径向与轴向受力进行有限元分析与计算。

(3)航空飞行器设计方面。目前世界最先进的飞行器都注重对于翼面涡升力的利用以增加飞行器飞行时的升力，比如我国的歼20威龙战机。具体为利用飞行器机翼前方的边条等结构产生脱体涡旋并流经于机翼上表面，显然该脱体涡旋的轴向与翼面平行。根据式(7)(8)(9)的分析可知，此时涡旋在流经机翼上表面而对机翼产生的径向作用力即为涡旋对机翼产生的涡升力，也即本文相关的分析方法与计算结果在航空航天飞行器设计上也有应用与参考的价值。