一种新型高阶连续的点对点运动轨迹规划算法
肖友刚,朱铖臻,李 蔚,韩 锟
(1.中南大学 交通运输工程学院,长沙 410075; 2.轨道交通安全关键技术国际合作联合实验室(中南大学),长沙 410075)
点对点运动广泛存在于机器人、数控装备、起重机械等领域。利用目标位置与当前位置的误差进行反馈控制,是很多点对点运动控制系统普遍采用的算法,这种方法存在着初始控制量大、过程不可控以及振动和冲击较大等缺陷。为了解决这个问题,通常采用轨迹规划法。合理的点对点轨迹规划应该将最大速度、加速度、加加速度等进行合理约束,并能根据被控对象特点有效调整加、减速过程,且保证系统平稳运行。目前,大多数轨迹规划是根据点对点运动所经历的加速、匀速、减速过程构造分段函数,然后利用各种方法对各段的衔接处进行平滑处理[1-6]。文献[2]将取放路径分解为两个正交的坐标轴,基于三次B样条曲线设计了高速取放并行机器人的四阶连续平滑轨迹。文献[7]建立了基于四元数的直线与圆弧运动的位姿模型,并采用弧长增量法插补技术实现了机械手空间轨迹规划。文献[8]将三角函数与直线连接组成加速度曲线,提出一种加加速度无突变且起止端连续的S型加减速规划算法。文献[9]采用五阶S曲线加减速方法对电机启动输入信号进行规划来抑制系统扭振,并运用粒子群优化算法选取五阶S曲线参数。文献[10]以循环计算方式获得加速段的运动距离与速度、最大速度的作用时间,提出了四阶S型轨迹规划算法。文献[11]通过设计机器人末端位置和姿态的数学表达式,在过渡节点之间采用一种有限项的正弦级数进行曲线拟合,提出了一种工业机器人连续轨迹规划过渡算法。文献[12]将两个周期不同的三角函数叠加,构造了伺服电机加减速曲线,降低了伺服电机的功率要求。文献[13]将速度和位移方程转换为单一凸形函数,并根据加速度、速度约束条件进行修正,提出了一种高效的加减速时间规划算法。文献[14]针对加速度的不连续变化,研究了一种基于S型速度曲线的轨迹规划方法。文献[15]使用五次多项式修改生成的轨迹,给出了由三点确定一般平面曲线的条件,提出了一般曲线插值方法,在此基础上设计了一种新轨迹。文献[16]将取放路径分解为两个正交的坐标轴,基于三次B样条曲线设计了高速取放并行机器人的四阶连续平滑轨迹。根据标准逻辑函数构造了分段S型加速度函数,得到了一条在速度、加速度、加加速度约束下四阶可微的轨迹。文献[17]将三次多项式和贝塞尔曲线相结合,设计了起、始点都光滑的轨迹。文献[18]探讨了最大速度曲线的特点,提出了一种最大或最小加速度的简便计算方法。文献[19]为减少高速运动阶段的残余振动,设计了一条加加速度约束下的非对称运动轨迹。文献[20]提出了一种基于相平面分析的轨迹规划法,可将台车速度、加速度以及负载最大摆幅始终约束在允许范围内。文献[21]利用三角函数设计了S型速度曲线,并利用其对旋转起重机两级残留摆角进行了控制。
综上可以看出,绝大部分轨迹规划都以梯形、S型速度或加速度曲线为基础,生成的轨迹表达式都是在加速、匀速、减速段的衔接点存在断点的分段函数。采用高次多项式、在衔接点采用正弦、余弦、样条或者双曲正切等光滑函数过渡,可以提升轨迹的平滑性和可微的阶次,但是这种方法通常增加了曲线衔接点的个数,使曲线表达形式更加复杂,时间规划更加困难,而且这些曲线参数众多,难以根据被控对象要求对启停进行针对性调整,使其效率或精度受到影响。
本文利用两段双曲正切函数构造衔接点在匀速段的非对称S型速度曲线,并将S型曲线与跟踪微分器结合,生成一种高阶连续的点对点运动轨迹(HCPPMT),其具有结构简单、光滑、冲击强度可控、各阶段的快慢程度可调、适用范围广等优点。与其他两种轨迹的性能指标进行对比,说明了HCPPMT的优越性。
1 高阶连续的点对点运动轨迹规划
点对点运动要求启动平稳、停车精准,而其所经历的加、减速阶段势必对其产生冲击,缓慢运行可减少冲击,但低下的效率使人难以接受。因此,需要根据被控对象特点,设计一条冲击强度可调、在匀速段能以最大速度运行、终点恰好为目标点的高效运动轨迹。S型曲线包含加、减及匀速3个阶段,符合点对点运动的特点,因此,先构造各阶段状态都可按需调整的S型曲线。为了避免S型曲线在加速、匀速、减速段的衔接点出现断点,构造一个具有加速、匀速、减速特点,且能光滑过渡的函数就很关键。
以v1表示运动点的实时位置,sd表示目标位置,当v1∈[0,sd/2],即运动点在起点和中点之间时,利用双曲正切函数设计包含加速和部分匀速段、且变化率可调的光滑连续曲线S1:
f1(v1,sd)=-kd·tanh[(v1+ε)·r1]
(1)
式中:kd为额定速度;r1为加速调节因子,可调节加速阶段的快慢程度,r1∈R+,r1越小,近似线性部分斜率越小,越平缓;ε为启动加速度调节因子,用于调节启动加速度。
当v1∈(sd/2,sd],即运动点在中点和目标点之间时,设计包含部分匀速和减速段、且变化率可调的光滑连续曲线S2:
f2(v1,sd)=kd·tanh[(v1-sd)·r2]
(2)
式中r2为减速调节因子,可调节减速阶段的快慢程度,r2∈R+。
将曲线S1和S2在中点进行衔接,形成包含加速、匀速及减速段的S型曲线:
(3)
该曲线中点附近处于匀速段,保障了整个S型曲线的连续性,利用双曲正切函数的平滑特性实现了点对点运动中加速、匀速、减速阶段的平滑过渡,有效避免了传统点对点运动轨迹规划中分别设计加速、匀速、减速段,然后采用平滑函数连接各段的繁琐过程,有效克服了传统设计中加速、匀速、减速衔接点处高阶不可微、使系统冲击和振动大的弊端。
被控对象启动时相当于被施加了一阶跃信号,该信号高阶不可微,会对被控对象造成严重冲击,阶跃信号经过跟踪微分器后,其输出曲线变为一条平滑曲线,可有效消除初始点高阶不可微的问题,因此对0点到v1-sd点用跟踪微分器处理,得
(4)
式中r为速度调节因子,可调节被控对象的运行速度,r∈R+。
对式(3)、(4)进行综合,得到速度、加速度和加加速度始终有界,可准确收敛至目标点,且高阶连续的点对点光滑运动轨迹(HCPPMT):
(5)
从HCPPMT的构造过程可以看出,在中点处存在衔接点,处理不当会产生断点,致使其高阶不可微。为克服这一缺陷,应使式(3)在sd/2邻域都处于匀速段。在目标点较远时,式(3)可保证被控对象以最大速度匀速运行较长距离,不会出现断点。而目标点很近时,若加、减速阶段运行的总距离等于sd,则意味着加速到最大运行速度后就需要减速,这时就会出现拐点,使其高阶不可微。因此,需调整速度调节因子r,使速度至少在sd/2邻域的2N个计算步长内都以最大速度匀速运行,N表示可微的阶数。最大运行速度根据目标点距离sd,加速阶段和减速阶段的调节因子r1、r2,额定速度kd,速度调节因子r,用龙格库塔法通过数值计算确定。
式(5)描述的高阶连续点对点运动轨迹具有如下性质:1)收敛至目标点sd处;2)速度始终有界,且r∈[0,2]时,0≤v2≤kd;3)加速度和加加速度始终有界。
2 高阶连续的点对点运动轨迹性质证明
定理1高阶连续的点对点运动轨迹(HCPPMT)收敛至目标位置sd处。
考虑到启动加速度调节因子ε的数值很小,为使证明过程简洁明晰,将其忽略不计。
构造如下函数h(v1):
(6)
式中Q=ln(cosh(r1sd/2))。当v1≤sd/2时,ln(cosh(r1v1))≤ln(cosh(r1sd/2)),又ln(cosh(r1v1))≥0,且kd、r、r1均为正数,因此式(6)≥0。
将式(6)对时间求导,可得
(7)
构造如下Lyapunov候选函数:
(8)
根据式(6)可知,V为恒大于等于0的函数,将V对时间求导,可得
(9)
由式(9)≤0可知,HCPPMT是Lyapunov意义下稳定的。

综合式(3)、(5)可知,当t→∞时,f(v1,sd)=0,因此可得
(10)
定理2HCPPMT的期望轨迹速度始终大于0且有界,且r∈[0,2]时,0≤v2≤kd。
证明构造新函数:
(11)
令G(v1)=g(v1)+f(v1,sd),接下来证明G(v1) ≥0。
当0≤v1<1/(2r1)时,
G(v1)=kd(2r1v1-tanh(r1v1))
(12)
对式(12)针对v1求导,可得
(13)
因此,在[0,0.5/r1]内,G(v1)为单调递增函数,又因为G(0)=0,因此在[0,0.5/r1]内,G(v1)≥0。
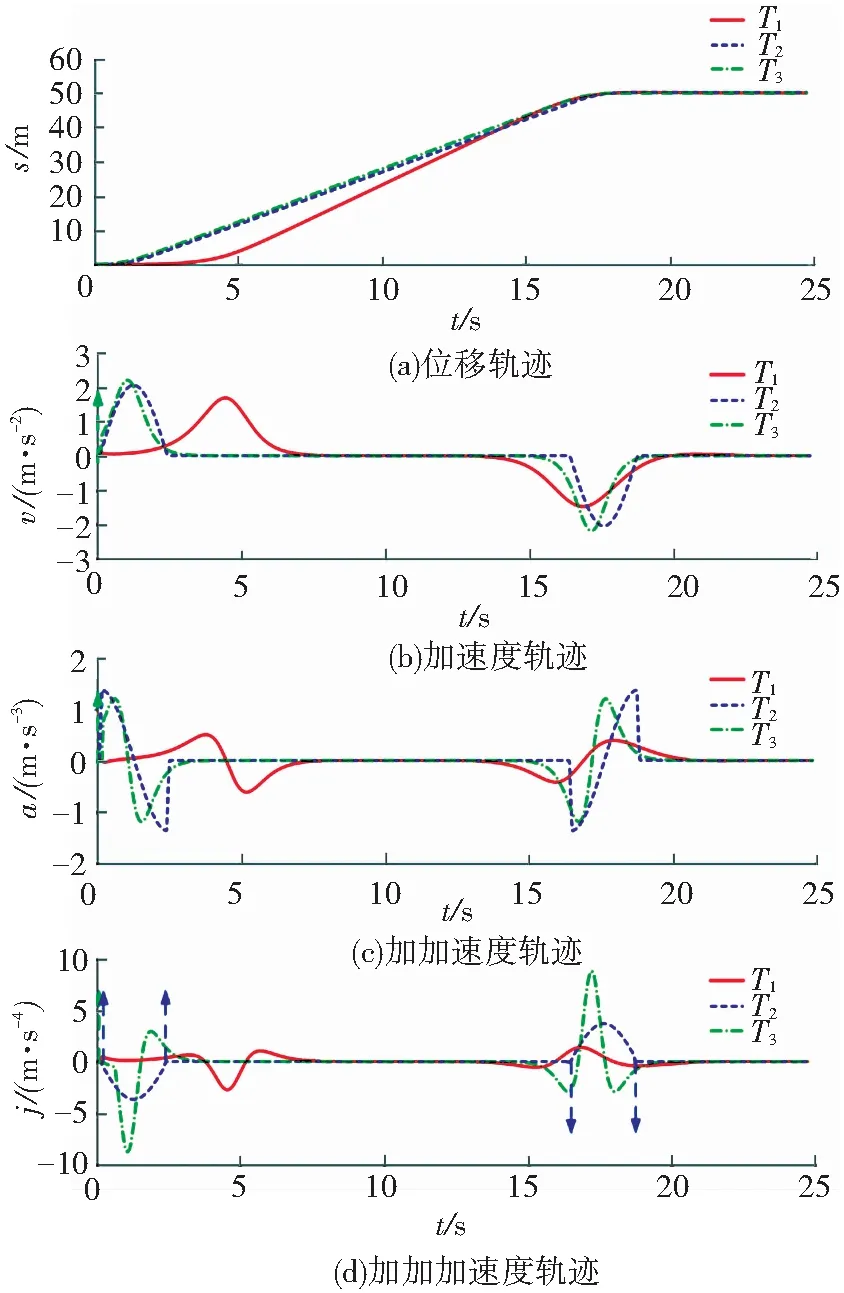
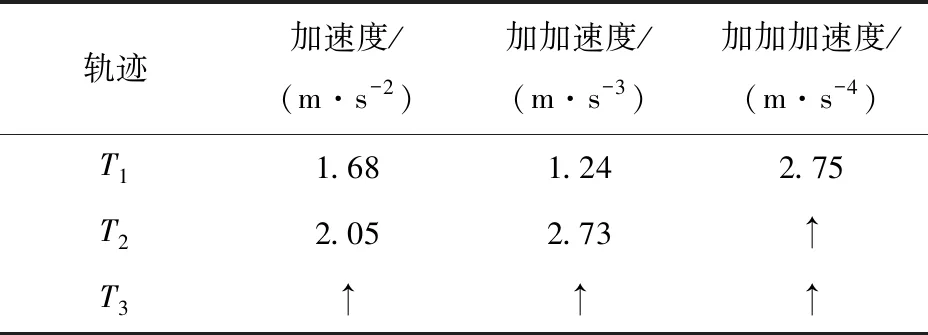
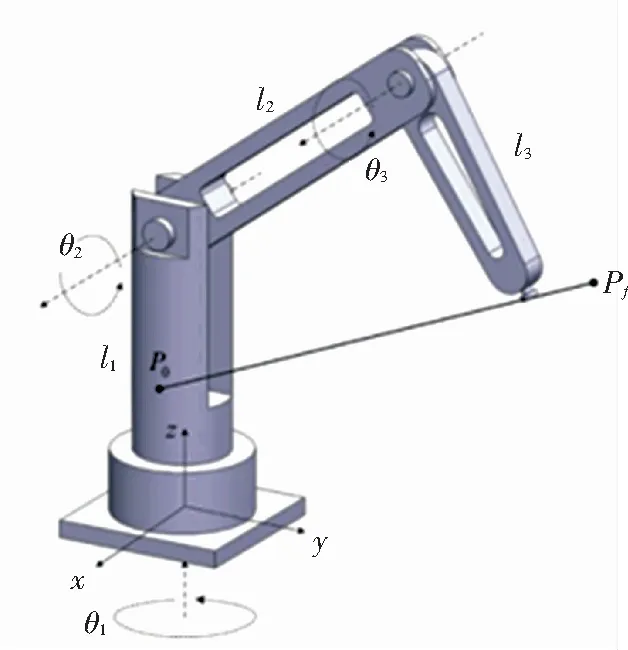
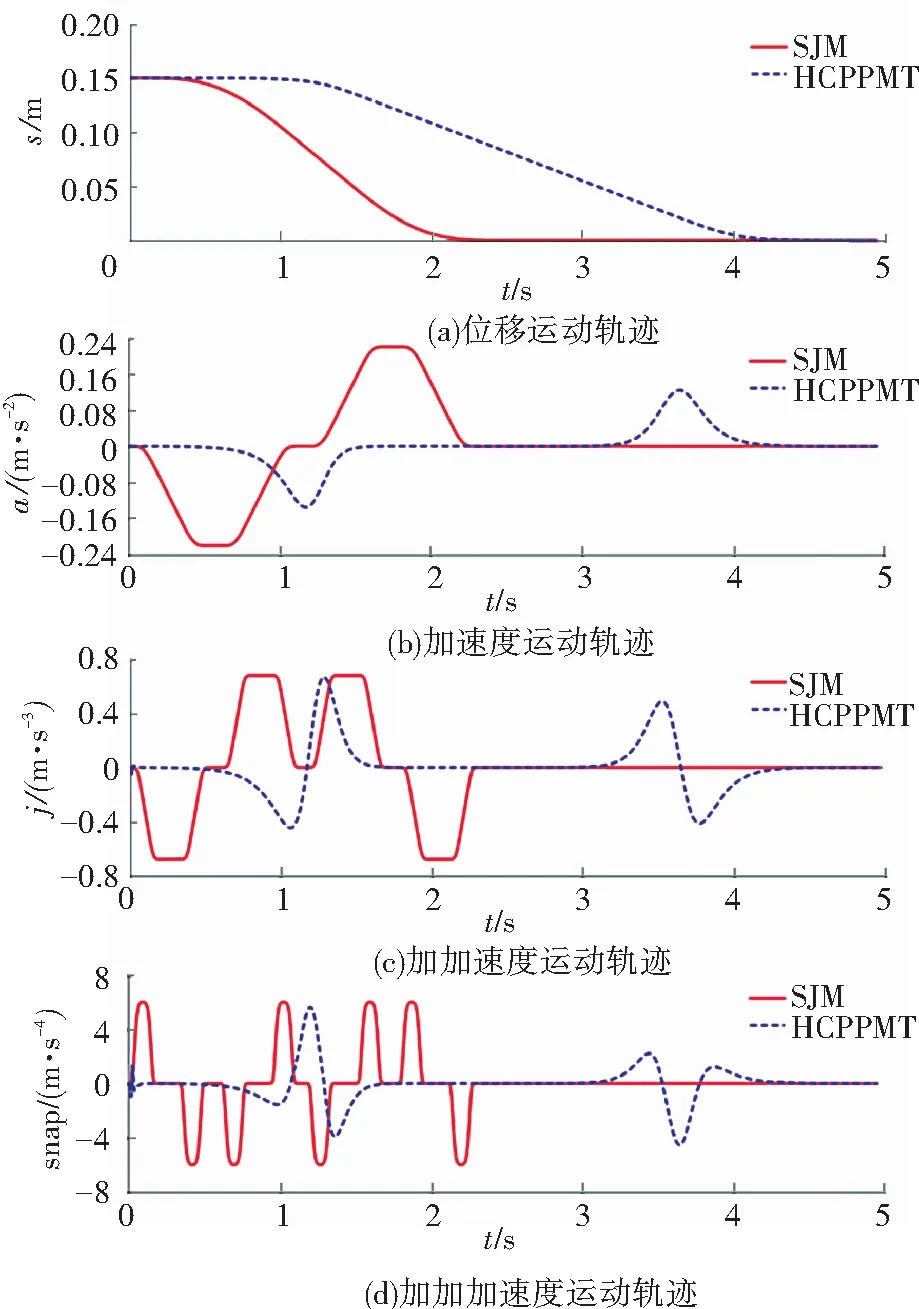
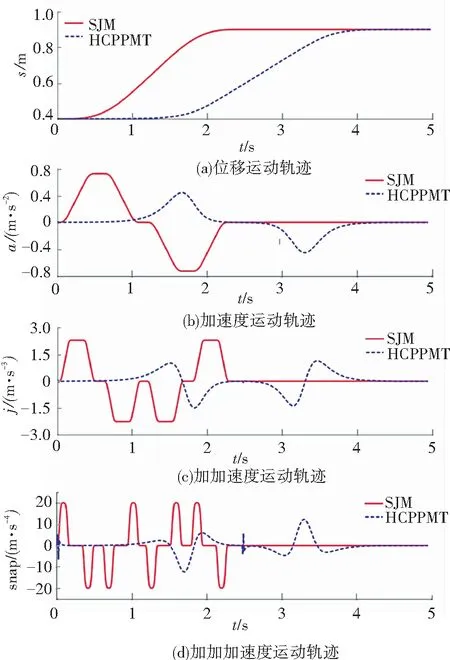
当1/(2r1)≤v1<(2sd-1)/(2r2)时,很显然G(v1)≥0;当(sd-0.5)/r2≤v1 G(v1)=kdtanh(r2(v1-sd))-2kd(r2v1-sd) (14) 对式(14)中的v1求导,得 (15) 因此,在[(sd-0.5)/r2,sd/r2]内,G(v1)为单调递减函数,又因为G(sd)=0,因此,在[(sd-0.5)/r2,sd/r2]内,G(v1)≥0。 综上证明可得,在[0,sd/r2]内, -f(v1,sd)≤g(v1) (16) 接下来构造一个新微分方程: (17) (18) v1=c1eψ11t+c2eψ12t (19) (20) 其中:c1、c2为待定参数(根据初始状态确定),kd为额定速度,显然式(20)是有界的。 由于t=0时,v1=0,将其代入式(19),可得 c1=-c2 (21) 由v1≥0可知,c1为正数。 对式(19)求导,并结合式(21),可得 v2=c1(ψ11eψ11t-ψ12eψ12t) (22) (23) (24) 对式(24)求导,得速度v2: (25) 对式(25)求导,并将t1代入,得 (26) 当t2≤t≤t3时, (27) (28) 这是一个典型的二阶系统,当r2≤1/kd时,其阶跃响应可以无超调地跟踪设定值sd,因而其位移是有界的,当然速度也是有界的。又由于无超调的阶跃响是单调上升的,因此当t2≤t≤t3,r2≤1/kd时,v2>0且有界。 由于所规划轨迹的最大速度在匀速段,而匀速段所在区间为[t1,t2],该区间内的最大速度为rkd/2,因而整个区间的速度都小于rkd/2。 综合以上分析,可得期望轨迹速度始终大于0且有界,且r∈[0,2]时,0≤v2≤kd。 定理3HCPPMT的期望轨迹加速度和加加速度分别有界。 根据式(23)、(26)、(27),显然加速度有界。 将式(5)对时间求导,得 (29) 由于加速度有界,且tanh函数为有界函数,因此式(29)有界,即加加速度有界。 对不同被控对象,在加速、匀速、减速阶段有不同要求。譬如:为提高效率,起重机械要求较快加速到最大运行速度后匀速运行,为保证安全,其最大运行速度也要根据环境风速进行调整,减速阶段则要求缓慢地停靠在目标点,以实现精准定位。因此,有必要研究可调参数对HCPPMT各阶段状态和冲击强度的影响规律,使其在不同的应用场合发挥最大效能。 为研究最大速度调节因子r对HCPPMT的影响,令sd=30 m、kd=2 m/s、ε=0.01、r=2、r2=0.4,当r分别取2、1.61和1.24时,位移、速度、加速度随时间的变化如图1所示,从图中可以看出,当r等于2时,轨迹的最大匀速运行速度等于额定速度。r越小,最大匀速运行速度越小,在作业距离一定时,耗时也越长。因此,作业距离越远,应使r越大,以便尽可能提高作业效率,但r不能大于2;近距离作业时,则应使r较小,但太小会降低作业效率,因此以在sd/2邻域的2N个计算步长内都以最大速度匀速运行为前提。对在室外环境中作业的起重机械,为保证安全,应根据风速等级,选择合适的r值。 为研究加速调节因子r1对HCPPMT的影响,令sd=30 m、kd=2 m/s、ε=0.01、r=2、r2=0.4,当r1分别取0.65、1和1.8时,HCPPMT的位移、速度、加速度随时间的变化如图2所示,从图2中可以看出,r1越小,轨迹初始阶段越平缓,到达最大速度的时间变长,运行规定距离所耗费的时间也越多,随着r1的增加,加速度变大,冲击强度增加,到达最大速度的时间变短,匀速段和减速段提前,但最大速度大小和减速阶段状态不受影响。因此,对于需要慢启动的精密机械,应取较小的r1值,以减小冲击,而对于行程较长的起重机械,在不超过最大加速度的前提下,则宜使用较大r1值,以便提高效率。 图1 参数r对HCPPMT轨迹的影响 图2 参数r1对轨迹的影响 为研究减速调节因子r2对HCPPMT的影响,令sd=30 m、kd=2 m/s、ε=0.01、r=1.24、r1=1, 当r2分别取0.2、0.28和0.36时,HCPPMT的位移、速度、加速度随时间的变化如图3所示,从图中可以看出,在进入减速段前,整个轨迹曲线保持不变,但r2越小,进入减速段的时间越早,使匀速段的时间变短,减速段的时间变长,完成整个作业过程的时间增多,但变化趋势越平缓,接近目标点时的速度也越慢,对于需要在目标点精确对位的精密装备,如岸桥起重机,宜选择较小的r2值。 图3 参数r2对轨迹的影响 为了检验HCPPMT的效果,取sd=20 m、kd=5 m/s、ε=0.01、r=1.28、r1=0.5、r2=0.2,计算步长取0.05进行仿真,得仿真结果T1。同时,在相同目标位置和计算步长下,将S型速度曲线的仿真结果记为T2,S型位移曲线的仿真结果记为T3。 S型速度曲线采用文献[22]中的形式,为便于对比,将角度转换成位移: (30) 其中:yc为该轨迹的最大速度,t1为加速阶段时间,t2为匀速阶段时间,T为总时间,具体参数取值分别为yc=3.065 m/s,t1=2.345 s,t2=12 s、T=18.69 s。 S型位移曲线采用文献[23]中的表达式: (31) 其中:ve为最大速度,ae为最大加速度,κ为初始加速度调节因子,κ=1.4,ve=3.056 m/s,ae=2.2 m/s2。 将仿真时间步长设置为0.01 s,仿真结果如图4及表1所示。 图4 3种轨迹的运动状态随时间的变化曲线 表1 3种轨迹各项指标最大值对比 图4中自上至下分别为T1、T2、T3的位移、加速度,加加速度,加加加速度随时间t的变化曲线,从图中4(a)可以看出:3种轨迹几乎同时到达指定位置,也就是在合适条件下它们的运行效率基本相同。从图4(b)及表1可以看出:轨迹T3的加速度在初始阶段出现了突变,说明利用轨迹T3进行跟踪控制时,在起动时需要很大驱动力,这势必要求提高执行器的功率,而且会对系统产生严重冲击,T1、T2的加速度都是连续的,但轨迹T1的最大加速度更小,说明所需的最大驱动力更小,对执行器的最大功率要求也就更低,有利于降低成本,而且T2在各段(加速、匀速、减速)衔接处出现了明显转折,而轨迹T1的加速度在整个过程中都比较平滑,因而利用T1进行轨迹跟踪控制,系统运行更平稳。从图4(c)及表1可以看出:T3初始阶段的加加速度也出现了突变,会对系统产生很大的柔性冲击,使其大幅振动,T2则在各段衔接处出现了最大值为2.73 m/s3的跃变,会对系统产生明显的冲击和振动,而T1加加速度的最大值为1.24 m/s3,远小于T2、T3的加加速度最小值,并且T2的加加速度平滑且连续,不会对系统产生大冲击和振动。从图4(d)可以看出,轨迹T2、T3的加加加速度在各段衔接处都出现了突变,而轨迹T1的加加加速度光滑且连续,且最大值只有2.75 m/s4,即使进行更高阶微分,都将是平滑且连续的,因此特别适用于需要进行高阶微分的场合(图中↑表示在该时刻,纵坐标值为无穷大值)。 三自由度机械臂运动轨迹曲线对机械臂末端运动有着重要影响,如果轨迹的加速度或者加加速度过大,会使机械臂在运行过程中出现振荡、使运动关节经受大冲击,太大的加速度还将使机械臂执行器饱和,使机械臂无法完成既定任务。三自由度机械臂的结构如图5所示,其中,l1、l2、l3分别表示机械臂1、2、3的长度,分别为0.85、0.95、0.65 m;θ1、θ2、θ3分别表示机械臂1、2、3的转动角度,末端执行器坐标为(px、py、pz),机械臂轨迹规划是通过对机械臂末端执行器空间坐标的x轴、y轴、z轴进行点对点规划,再利用末端执行器坐标和机械臂的转动角度关系式,将设计好的x轴、y轴、z轴的轨迹转化为关节的转动,实现末端执行器的空间运动。末端执行器坐标和机械臂的转动角度关系式可用式(32)描述[16]: (32) 图5 三自由度机械臂的结构 为了验证HCPPMT的有效性,在同样条件下将HCPPMT和文献[16]设计的光滑7段式三自由度机械臂末端执行器运动轨迹(SJM)进行对比,SJM的表达式为 j(t)=sign(D)· (33) 式中:D为定位距离,Jmax为最大加加速度。 与文献[16]一样,根据表2中机械臂末端执行器起始点、目标点坐标和路径距离用HCPPMT算法进行仿真,并与SJM进行对比,得到的结果如图6、图7、图8和表2所示。从这些图中可以看出,在整个过程中,这两种方法的加速度、加加速度、加加加速度都光滑连续,但HCPPMT法在这3个指标上均比较有优势,其最大值都小于SJM法的最大值,然而,HCPPMT法到达目标点的时间稍长,这是由于加入跟踪微分器后虽然进一步保证了HCPPMT的高阶可微性,但是使启停过程变得比较平缓,因此需要探寻既能使两段双曲S型轨迹高阶可微,又不影响启停快慢的函数与其结合,这是后续将深入研究的课题。 表2 末端执行器对应的坐标和距离 图6 末端执行器x轴方向的运动轨迹 图7 末端执行器y轴方向的运动轨迹 图8 末端执行器z轴方向的运动轨迹 从表3可以看出,为了在相同时间内到达目标点,采用SJM法,y轴方向的最大加速度比z轴方向的最大加速度大1.18 m/s2,比x轴方向的最大加速度大1.69 m/s2;y轴方向的最大加加速度比z轴方向的最大加加速度大3.63 m/s3,比x轴方向的最大加加速度大5.22 m/s3;y轴方向的最大加加加速度比z轴方向的最大加加加速度大32.07 m/s4,比x轴方向的最大加加加速度大46.12 m/s4;而采用HCPPMT法,y轴方向的最大加速度比z轴方向的最大加速度大0.70 m/s2,比x轴方向的最大加速度大1.18 m/s2;y轴方向的最大加加速度比z轴方向的最大加加速度大3.29 m/s3,比x轴方向的最大加加速度大4.56 m/s3;y轴方向的最大加加加速度比z轴方向的最大加加加速度大26.32 m/s4,比x轴方向的最大加加加速度大35.16 m/s4。因此,定位距离越大,采用HCPPMT法的加速度、加加速度、加加加速度的增量越小,对执行器功率的要求越低,出现执行器饱和而不能完成指定任务的概率就越小;对系统的冲击越小,系统振动幅度也就越低,系统的运动精度也就越高。 表3 末端执行器加速度、加加速度、加加加速度最大值 1)通过利用两段双曲正切函数构造衔接点在匀速段的S型速度曲线,并将其与跟踪微分器结合,生成了结构简单、高阶连续的点对点运动轨迹,实现了点对点运动加速、匀速、减速过程的平滑过渡,减少了加速、匀速、减速段切换过程中的冲击,增强了运动的平稳性。 2)通过调整HCPPMT的相关参数,可调节加、减速阶段的快慢程度、匀速阶段的最大速度、作业时间,使HCPPMT的平滑程度、冲击强度可控,各阶段状态可调,且HCPPMT的收敛性及物理性质都通过了严格的数学证明,适用于不同应用场合。后续将利用HCPPMT对数控机床、起重机等进行轨迹跟踪控制研究。 3)通过和其他两种轨迹对比,以及在三自由度机械臂末端执行器轨迹规划上的应用,说明了HCPPMT的优越性。
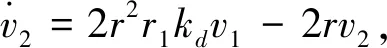
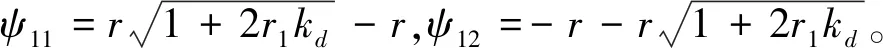

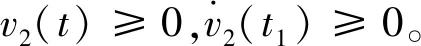
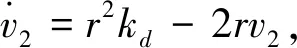

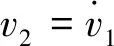
3 可调参数对HCPPMT的影响分析



4 3种轨迹生成算法的对比分析
5 HCPPMT在三自由度机械臂轨迹规划中的应用分析



6 结 论

