实时工况仿真场景下蒸汽发生器液面智能预测模型的实现与验证

佘兢克，王佳妮，杨溯源，薛时雨

（湖南大学 信息科学与工程学院，长沙 410082）

0 引言

核能是一种具有丰富储量且高能低耗的清洁能源，是当下生产力高度发展、对能源有高度需求的工业4.0时代的首选。作为核电站中核岛和常规岛的连接枢纽，蒸汽发生器在核电站中的重要地位仅次于反应堆。目前，核电厂普遍选取传统PID控制法进行各级各类设备的控制管理。但PID是一种对于线性定常系统有效的控制策略，而对于蒸汽发生器水位这种时变、复杂的非最小相非线性系统的控制效果有所欠缺，并且PID中的积分部分存在着积分饱和的隐患，无法精准、及时、有效地进行控制[1]。

当前解决蒸汽发生器控制问题多以物理原理为切入点，通过对PID控制器参数的整定方式进行改进进而优化控制效果[2]，如M. Davanipour[3]等人提出的基于模糊小波神经网络模型的自整定PID控制法，M.G. Na[4]等人研究的模糊控制器的自整定方法，潘玉成[5]等人提出的基于模糊RBF神经网络的PID控制法，苏应斌[6]等人提出基于CFNN的控制法，Kento Kinoshita[7]等人提出通过虚拟参考迭代调整法均为使用神经网络实现PID控制器实时整定参数。然而，这种通过原理角度进行优化的方式实施成本高，并且无法彻底解决蒸汽发生器系统时变性、非线性给系统控制带来的困难。

上述方法中的参数调整方法都是基于蒸汽发生器本身物理模型以及液面变化的物理模型来构建和实施，方法的精确度依赖于物理模型构建的精确度。对于蒸汽发生器这样一个非线性时变复杂系统来说，精确构建其运行时的物理模型面临非常巨大的挑战和困难，也由此导致现行方法都存在无法完全捕捉蒸汽发生器液面变化等系统行为细节特点的问题。为了避免构建精准系统物理模型的“白盒子”问题，可以使用海量历史数据训练精准的机器学习模型，通过数据驱动方法，基于系统过往行为特点来预测系统后续的行为趋势。将困难较大的白盒子转换为直观简单的黑盒子，依赖强大的数据存储和处理平台，能够在预测实时性和精准度上达到理想的效果。由此获得的预测结果成为精准的决策依据，为PID控制系统的智能优化奠定了基础。

本文工作采用长短期记忆模型（Long-Short Term Memory，LSTM）作为蒸汽发生器液面工况的预测方法。LSTM作为比较成熟的深度学习方法，适用于长时间序列数据的跟踪和预测。它使用“门”的概念来区分和管控不同重要性的数据流，使与预测参数密切相关的数据能够持续保留在循环迭代过程中，从而保证在长时间序列中预测结果的准确度[8]。而使用LSTM方法来预测核电站的工况和参数已经证明为可行并高效[9]。LSTM模型中神经元的结构如图1所示。

图1 LSTM神经元结构图Fig.1 LSTM neuron structure diagram

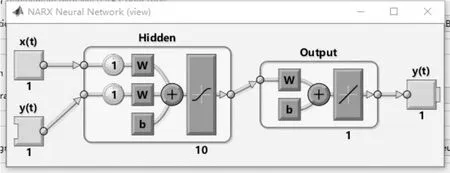
图2 LSTM模型网络结构展开图Fig.2 LSTM Model network structure expansion diagram

应用智能方法的控制系统相比于传统控制具有以下优势：

①具有人的学习能力和控制策略；②适应性强[10]；③较强恢复能力；④变结构非线性；⑤较强组织功能；⑥支持混合控制过程[11]。

因此，应用人工智能方法来辅助传统控制手段，能有效提升系统对控制对象的感知能力，进而使控制器的性能提升成为可能。

1 预测模型构建

智能预测模型采用LSTM方法设计，并通过仿真实验中该模型损失函数的分析来验证该模块模型在诸如蒸汽发生器液面调控这一类长时间序列过程中的可行性。

1.1 智能预测单元的设计

预测单元是本文智能预测模型的核心元件，其原理应用了循环神经网络中的LSTM结构。LSTM模型具有RNN的反馈结构特征，又改善了神经元的内部结构，因而能够解决长期问题中的梯度消失和梯度爆炸问题，在处理长序列问题中具有比传统RNN更佳的性能。LSTM模型通过引入“遗忘门”的结构，不断减少向下传递的内容[8]，并引入“细胞状态”实现长期学习。

本文基于LSTM模型结构设计具有一层隐藏层、一层输出层的网络，结点数量分别为10和1。

其中，输出门和遗忘门选取sigmoid函数作为激活函数，输入门则选取sigmoid函数和tanh函数作为激活函数。模型的搭建平台选取MATLAB中的深度学习工具箱。经过有效训练神经网络的模块通过SIMULINK模块生成功能，直接生成如图3所示的封装单元。

图3 LSTM预测单元（封装）Fig.3 LSTM Prediction unit (package)

1.2 智能预测模型的训练

本文选取工业级仿真机模拟的数据进行训练。选取仿真数据中6014个时间点的数据，归一化处理并添加信噪比为80的高斯噪声以增加数据多样性并预防过拟合现象。经过预处理的数据被划分为训练集、验证集、测试集三部分，分别占总数据量的70%、15%、15%。训练算法选取深度学习工具箱中提供的L-M反向传播算法，该算法虽占用内存较大但训练速度较快。迭代的训练次数由深度学习工具箱自适应决定，决策依据为训练过程中损失值的变化情况。本文选取均方误差（MSE）为损失函数，训练次数为275次，训练过程中各数据集MSE的变化情况如图4所示，最终MSE值见表1。

表1 训练结果均方误差Table 1 Mean square error of training results

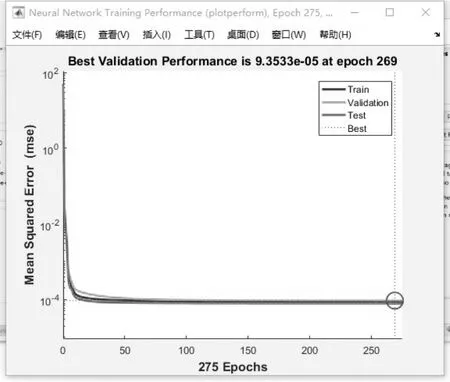
图4 均方误差变化Fig.4 Mean square error change

2 智能预测模型及其实时验证平台

基于LSTM的智能预测模型和传统PID液面控制模型组成了智能预测模型的实时验证平台。智能预测模型采用上文介绍的使用蒸汽发生器液面调控数据训练完毕的封装LSTM模型；同时，利用SIMULINK库中模块模拟搭建蒸汽发生器液面控制的PID控制模型。二者均使用一个观测模块输出的液面测量信号（即控制反馈）作为各自输入，形成两个独立回路。智能预测模型回路依据输入的液面信号预测出后续液面调控变化；PID控制回路以传统方式输出控制信号调节液面变化。通过对PID实际调控的液面变化与智能预测模型预测的液面变化对比，验证智能预测模型在指定工况场景下的预测精度。

2.1 传统PID控制模型

传统PID控制模型的实现是本文验证智能预测模型的重要基础，为了便于结合LSTM模型，首先以SIMULINK为实验平台设计实现蒸汽发生器的单冲量控制模型。传统控制模型以蒸汽发生器液位控制方框图（见图5）为理论基础[13]，在此基础上将元件抽象划分为计算、执行、反馈3个单元并另添加观测单元以便于观测实验结果。以下元件的设计与实现均源于平台SIMULINK。

图5 蒸汽发生器液位控制方框图Fig.5 Block diagram of steam generator level control

2.1.1 计算单元

计算单元包含误差计算模块和控制信号计算模块两部分。

误差计算模块对应于图5中标号1，选取SUM元件实现。如图6所示，用于计算蒸汽发生器实际液位高度与设定的标准值之差。

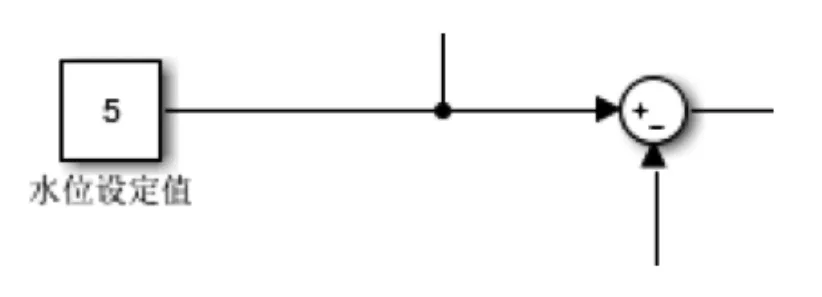
图6 误差计算模块Fig.6 Error calculation module

控制信号计算模块对应于图5中标号2，选取PID控制元件实现。如图7所示，用于根据当前误差给出控制信号，以调节液位高度，比例参数设定为35，积分参数设定为0.01，微分参数设定为25。

图7 控制信号计算模块Fig.7 Control signal calculation module

2.1.2 执行单元

执行单元包含执行器和物理过程两部分。

执行器对应于图5中标号3，选取增益元件实现。如图8所示，用于将上一级输出的控制信号通过内部封装的放大器等功能元件转化为具有控制给水阀能力的开度信号，调节参数设定为15。

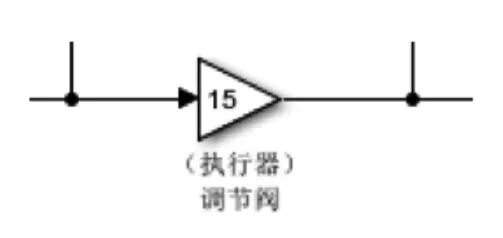
图8 执行器Fig.8 Actuator

物理过程对应于图5中标号4、5，通过多个元件协同模拟，包含施加外部干扰的给水扰动模块（选取脉冲信号实现）、模拟调节时间非瞬时过程的延时模块（选取延时函数实现）以及将水阀开度信号转化为水位高度的传递函数，其公式见式（1）[14]：

2.1.3 反馈单元

反馈单元用于将测量所得的液位真实数据反馈至计算单元，对应于图5中标号6，其主要元件为差压变送器，由增益元件实现。由于采用单冲量控制，因而增益参数设定为1。

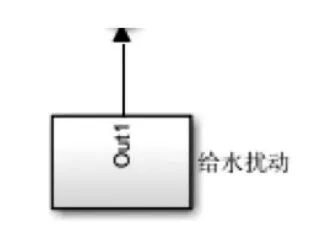
图9 给水扰动模块Fig.9 Feedwater disturbance module

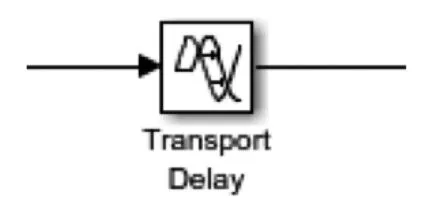
图10 延时模块Fig.10 Delay module

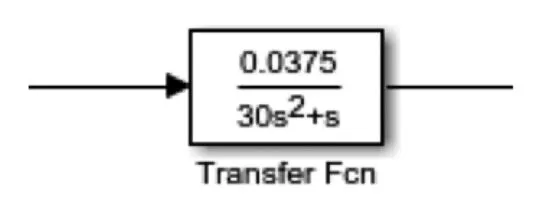
图11 传递函数Fig.11 Transfer function

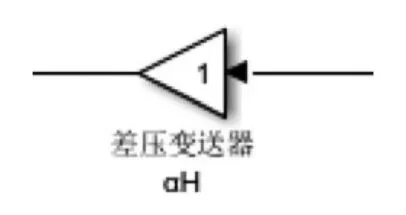
图12 差压变送器Fig.12 Differential pressure transmitter

图13 差压变送器数据采集子系统Fig.13 Differential pressure transmitter data acquisition subsystem

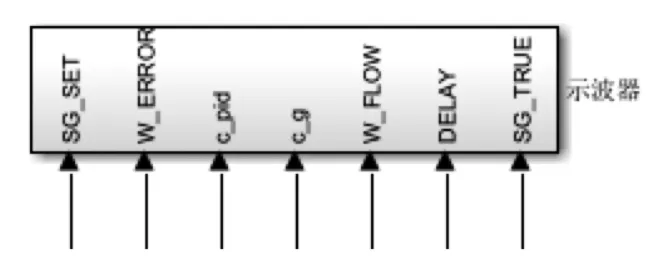
图14 执行器示波器子系统Fig.14 Actuator oscilloscope subsystem

2.1.4 观测单元

观测单元包括数据观测模块和图像观测模块两部分。

数据观测模块选取To Workspace元件实现，用于获取各信号的在采样时刻的数值，通过集成封装成数据采集子系统。

图像观测模块选取Scope元件实现，用于观测信号的变化情况，通过集成封装成示波器子系统。

2.2 验证平台集成

传统PID控制模型与智能预测模型的系统架构与交互方式如图15所示。经传统PID控制模型得到的真实水位变化数据在反馈到误差计算模块的同时也输入到预测单元，经预测单元处理得到的水位预测值与PID控制实现的水位值共同由观测单元的比较模块实现对比。

图15 验证平台的系统架构Fig.15 System architecture of the verification platform

在上述传统PID控制模型元件实现的基础上，根据图15的系统架构将各元件依次连接构成智能预测模型的总体验证平台。预测单元则根据其“预测未来水位数据”的功能添加在反馈单元与观测单元之间，使经测量得到的水位数据成为其输入信号。经预测单元处理后所得的预测值能够展示在观测单元中。另外，在智能预测模型的观测单元上另外添加了比较模块，以观察水位预测值与真实值之间的偏差，由SUM元件、To Workspace元件、Scope元件共同构成并加以封装，如图16所示。

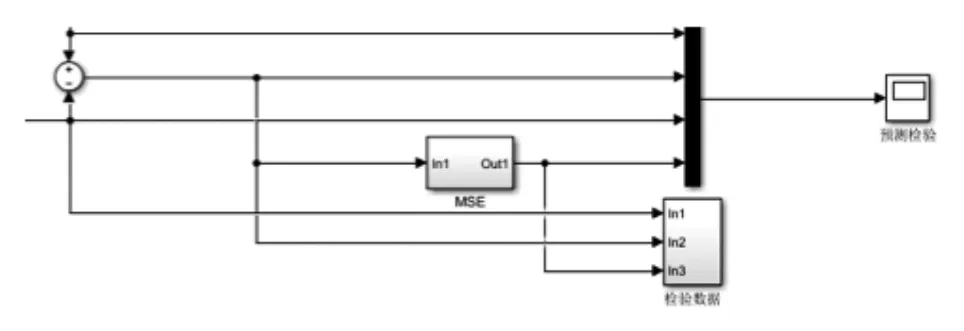
图16 比较模块Fig.16 Comparison module

最终生成的蒸汽发生器液面智能预测模型的实时验证平台如图17所示。

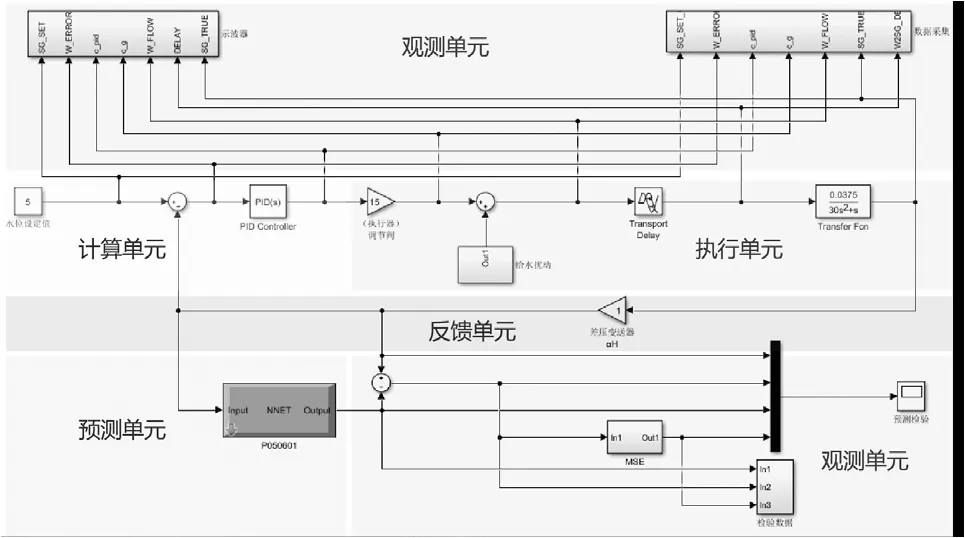
图17 智能预测模型实时验证平台Fig.17 Real-time verification platform of intelligent prediction model

3 智能预测仿真实验及结果分析

3.1 仿真实验准备

智能预测模型的仿真过程在MATLAB的SIMULINK上实现，其检测要点如下：

1）控制后的水位值是否最终收敛，若不收敛则需调整PID控制器的控制参数。

2）控制后的水位值收敛至稳态时，是否为最初的设定值。若错误，则需调整执行器或差压变送器的参数。

3）给水扰动是否发挥作用。若否，则需调整脉冲值的范围。

4）预测单元的水位预测结果。若得不到预测结果，则需检查归一化步骤、反归一化步骤、输入数据的格式和维度等。

5）预测结果与真实结果之间的误差以及均方误差。若误差或均方误差较大，则需考虑调整预测单元的神经网络结构，或重新训练预测单元，或预测单元是否出现过拟合现象。

3.2 实验结果及分析

工况仿真时长为200 s，且在仿真过程中周期性地给予系统水位扰动信号，形成“扰动-调整-稳态”的周期性水位波动，为对比分析提供多样化的分析样本。由于0时刻暂无反馈，预测结果初始为0。本文仿真实验与文献[9]中仿真过程的差别在于本文采用PID控制器实时产生的水位调节结果作为预测模型输入，在检验预测模型预测功能的同时，也检测其在实时工况环境下对工况变化的敏感度以及动态预测的准确性。

水位预测结果图像如图18所示，其中，(b)图与(c)图均为由(a)图放大的局部图像。

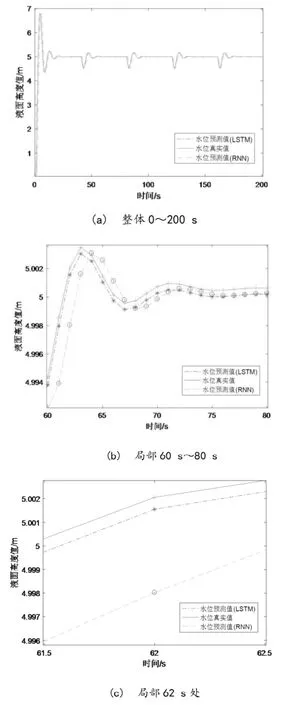
图18 水位变化真实值与两类模型预测值对比Fig.18 Comparison of the real value of water level change and the predicted value of the two types of models

如图18(b)所示，基于LSTM和RNN分别实现的预测单元产生的水位预测结果在整体变化上均符合实际水位趋势，但LSTM的预测结果明显更加贴合水位真实值。以第62 s为例，水位真实值与LSTM预测值的差别如图18(c)所示，相比于RNN的预测值误差更小。由此可见，智能预测模型的预测单元能够生成符合水位变化特征的预测值，且LSTM的预测效果优于RNN。

预测精度图像如图19所示，其中给出了LSTM和RNN两种预测手段在精度上的差别，并分别给出误差值和MSE值。

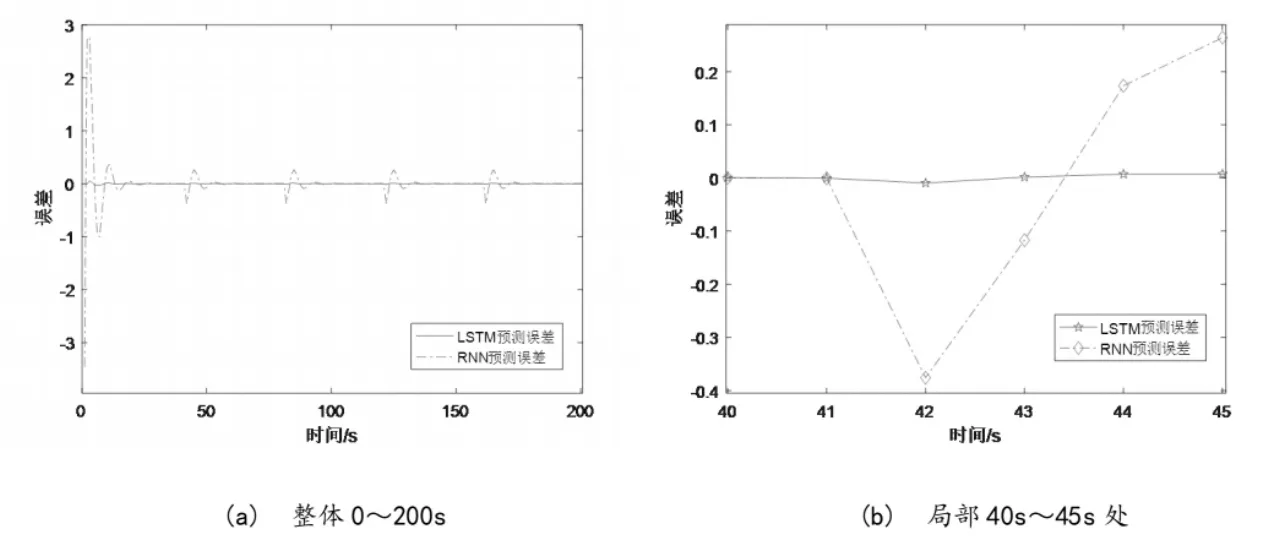
图19 预测误差对比图Fig.19 Comparison of prediction errors

如图20所示，由图像可直观看出LSTM预测结果的误差值明显低于RNN，且误差值图像波动更小，说明其预测效果稳定，适合用于非线性、时变性强的数据预测，例如蒸汽发生器的液面变化。在误差偏移量较大的第42 s处，LSTM预测误差值为6×10-3。从表2所示的不同采样点误差值也可以看出RNN预测误差值较高，不如LSTM预测值精确。从表3所示的预测损失值MSE来看，基于LSTM建立的预测单元的预测损失值基本在10-8量级，而且LSTM预测结果的MSE比RNN的更小且更稳定。同时可以看到，LSTM预测的MSE值在预测过程开始后较快地减小到并稳定在10-8量级，表现出了较快的计算收敛性，因此能够在更短时间内获得准确的预测结果。

表2 不同采样点误差值Table 2 Error values of different sampling points

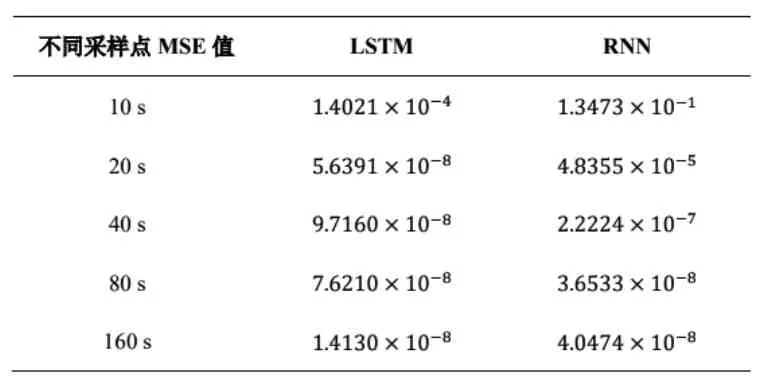
表3 不同采样点MSE值Table 3 MSE Values of different sampling points

4 结论

本文设计、实现并验证了一个基于LSTM方法的核电站蒸汽发生器液面智能预测模型，并采用与传统PID控制器相结合的方法进行了实时工况场景下的验证。PID控制器调控产生的水位反馈信号同时作为LSTM模型的输入，以此验证其对于工况水位变化的敏感性和预测的准确性。实验证明，LSTM模型能有效地响应水位变化并在较短时间内输出精确的水位预测值。其预测误差最小可以达到-1.1887×10-4，且预测误差水平非常稳定；其预测精度较高，神经网络运算损失值最低可达1.4130×10-8。同时，实验结果表明LSTM模型在预测过程中收敛较快，这对于需要及时获得工况预测结果来加强控制效果，或者提升安全系数的核电站仪控设备来说非常重要。可见，LSTM模型对于传统控制方法是非常有益的辅助和补充。未来进一步的工作可以专注于将LSTM的精准预测结果与传统控制机理结合起来，提高传统控制方法的智能化水平，从而提升核电站仪控设备的工作效率，为更加高效安全的核电站运行打下基础。

致谢

本文作者衷心感谢下列科研项目和单位对本文工作的支持：

1）湖南省自然科学基金项目，“基于预测控制的核电站快速响应与智能控制研究”（2018JJ2057）。

2）湖南省“湖湘高层次人才聚集工程—创新人才计划”（2018RS3050）。

3）2019年工业互联网创新—基于工业互联网平台的生产线数字孪生系统项目。

4）国家电力投资集团有限公司中央研究院。

5）中广核研究院有限公司。

6）湖南湘江人工智能学院。