考虑多种变量不确定性的梯级水电站中期调度及交易决策方法
卢 佳,李 刚,程春田,刘本希
(大连理工大学 水电与水信息研究所,辽宁 大连 116024)
0 引言
随着新一轮电改逐步推进,各省市建立起规则完善、体系健全的中长期市场[1]。中长期交易由于风险较小、收益稳定,成为市场参与者规避风险的“压舱石”[2-4]。同时,中长期市场还起到锚定现货市场价格的作用。对于流域梯级水电站而言,中长期市场可以很好地使其规避因径流不确定性而带来的运行风险,特别是对于误差较大的长期运行及交易计划,水电企业可以根据更加精确的预测结果,利用中期优化调度调整长期计划以及制定交易策略。
在中长期市场环境下,梯级水电传统的调度方式[5]受到了极大冲击。不同于其他电源类型的发电企业,水电在参与电力市场时不仅需要考虑交易阶段由市场结构、交易结算规则和竞价策略等因素导致的成交风险,还需要考虑运行阶段因径流时空分布不均匀、不确定以及梯级水电站水力、电力时空紧耦合等因素导致的运行风险。但是在参与月度中长期市场时,为追求更高收益,决策者通常采取多发电和高报价2种途径,中期径流和电价的预测值不可避免地存在误差,这可能导致发电量不足而无法履约或报价过高使竞价失败,因此,在中期调度背景下参与中长期交易时,需要考虑市场出清电价的不确定性和日径流的随机性使梯级水电站面临的两阶段风险,即中长期市场申报阶段的成交风险和中期调度阶段的运行风险,如何联合考虑上述风险并在相应阶段做出合理的决策,是当前我国水电面临的主要挑战。
目前,国内外学者针对上述问题已有一些研究。针对申报阶段的风险决策,文献[6]考虑构建风电出力的不确定集,并基于该不确定集将风电企业日前申报决策模型转化为鲁棒优化模型。文献[7]考虑需求侧资源的不确定性给负荷聚合商在双重市场的投标带来的困难,建立负荷聚合商在双重市场的投资分配和利润模型。文献[8]构建包含配电网运营商、分布式电源运营商、储能运营商和用户的增量市场模型,分析各主体间的市场关系和价格传导机制,并利用纳什均衡解的存在性条件构建增量市场环境下多主体参与的双层优化模型。针对运行阶段的风险决策,文献[9]采用Copula函数和条件风险价值构建耦合月度交易和日前增量交易的梯级水电站参与市场交易的风险分析方法;文献[10]在考虑电价不确定的同时,兼顾结算规则对梯级水电站在多尺度电力市场背景下月度发电计划制定的影响。文献[11-12]构建水电中长期优化调度和电量优化分配模型,分析交易组合的价格风险,寻求收益和风险的合理决策。
然而从使用场景来看,目前的研究尚有不足,主要体现在以下3 个方面:研究对象大多是以火电、风电为主体的,因此研究成果不适用于上、下游之间存在紧密水力-电力联系的梯级水电站风险决策问题;采取场景法处理不确定性问题时,为了使描述更为精确全面,通常要求场景数足够多,从而容易导致求解效率低下以及结果过于保守;研究大多单独考虑申报阶段的决策风险或运行阶段的履约风险,而实际使用中需要耦合这2类风险。
为了解决上述问题,本文引入我国西南某以水电为主的电力市场结构与交易结算规则,同时考虑中长期市场申报阶段、中期调度运行阶段的风险,提出联合信息间隙决策理论IGDT(Information Gap Decision Theory)与前景理论的梯级水电站中期运行及交易风险决策方法。首先考虑中期运行阶段的风险,使用IGDT配合鲁棒优化模型求解满足梯级水电站预定收益时日径流与市场出清电价相较于预测值的最大偏差幅度;然后根据不确定变量的波动范围考虑中长期市场申报阶段的交易决策风险,从有限理性的角度出发,使用前景理论对梯级水电站在中长期市场中的报价策略问题进行分析与研究,并建立相应的报价决策模型;最后以某梯级水电站为例,采用本文方法给出不同预期收益目标下日径流与市场电价的波动范围,并在该范围内根据梯级水电站不同风险偏好程度制定合理的申报决策与运行方案。
1 前景理论简介
前景理论[13-14]是一种计及决策者主观感受的方法,即决策者面对收益是风险规避的,而面对损失是风险偏好的,且面对损失时比面对收益时更加敏感。在实际中,决策者面对的是一个具有高度复杂性和动态性的电力市场,由此带来的很多不确定性风险问题使决策者难以满足“完全理性人”的假设,即决策者得到的信息是有限的,因此其对市场的预测总是存在一定误差。此外,对问题本质的有限洞察力也使决策者很难保证一致的风险偏好,从而体现出风险偏好变化的特点。与假设决策者为完全理性的“均值-方差”、风险价值/条件风险价值方法不同,前景理论假设决策者为有限理性,即决策者得到的信息是有限的,其风险偏好会随着客观因素的不同而变化,通常用前景价值作为决策依据。前景价值由价值函数和决策权重共同决定,计算公式为:
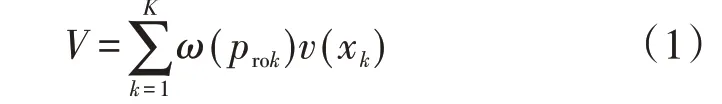
式中:V为前景价值;K为所有可能发生的事件数;prok为事件k发生的概率;ω(prok)为概率权重函数;xk为事件k的指标值;v(xk)为价值函数。
前景理论中,决策者的决策过程受其对决策方案所得收益的主观价值感受以及对收益实现概率的主观感知2个方面的影响。
价值函数表示根据决策者的主观感受形成价值,常用的价值函数为:
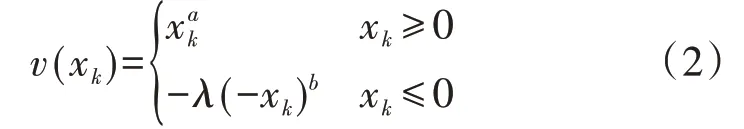
式中:a和b分别表示收益和损失区域价值幂函数的凹凸程度,反映了决策者对收益和损失的敏感程度,一般a,b≤1;λ反映了决策者对损失的厌恶程度,一般λ>1。
概率权重函数表示决策者对事件发生概率做出某种主观判断,常用的概率权重函数为:
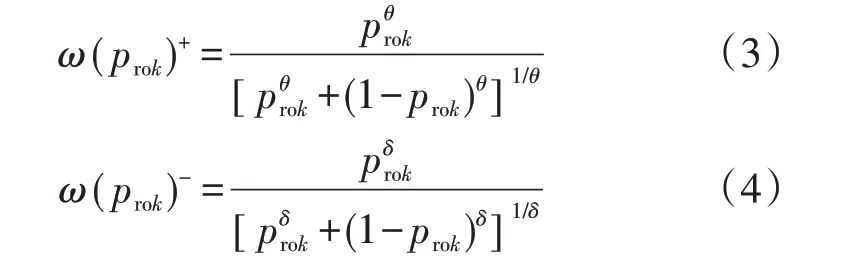
式中:ω(prok)+和ω(prok)-分别为决策者感知收益和损失时的概率权重函数;θ为决策者面对收益时的风险态度系数;δ为决策者面对损失时的风险态度系数。
2 联合IGDT与前景理论的风险决策模型
当市场主体评价某个决策方案是带来收益还是损失时,通常不是从总财富的角度考虑的,而是从财富变化的角度考虑的,主观价值的载体是财富的变化,而非财富的最终状态。因此梯级水电站评估参与市场的风险时,首先需要预先设定预期收益,然后根据售电收益评价不同的申报决策与运行方案,最后根据自身对风险的态度选择最优的决策方案。
2.1 梯级水电站中长期市场收益模型
本文研究的各电站市场份额占比很小,各电站申报方式对成交结果没有影响,因此可以认为它们是价格接受者。在市场中的交易采用按报价支付PAB(Pay-As-Bid)进行结算[15-16]。当各电站参与中长期市场时会根据预测的日径流与市场出清电价,制定相应的申报决策和运行方案。由于梯级水电站决策者为有限理性的价格接受者,无法获得对不确定性变量的无偏估计,因此按照预测的出清电价进行申报可能会因预测误差造成报价过高而导致竞价失败,此时申报失败的电量按照上网电价结算。同时由于天然径流存在较强的波动性,预测结果往往存在误差而导致中期调度运行阶段的交易合约无法完成或者超额完成,因此需要考虑违约部分的考核。梯级水电站售电收益为:
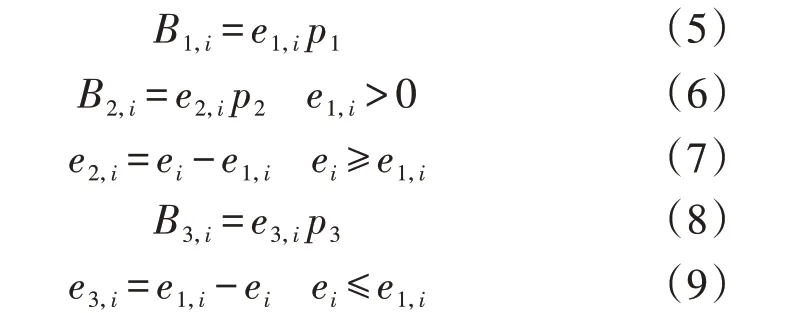
式中:B1,i、e1,i分别为水电站i的中长期市场收益和结算电量;p1为中长期市场结算电价;B2,i、e2,i分别为报价成功时水电站i的超额发电收益和超发电量;p2为超额电量结算电价;ei为水电站i当月的总发电量;B3,i、e3,i分别为水电站i的违约损失、违约电量;p3为违约考核电价。
2.2 梯级水电站中期优化调度模型
2.2.1 运行阶段优化调度目标函数
考虑到梯级水电发电成本主要由固定成本构成,并不影响模型优化,本文忽略不计。以一个月为调度周期,一天为一个时段,梯级水电站参与市场目标为总收益最大,其计算公式为:
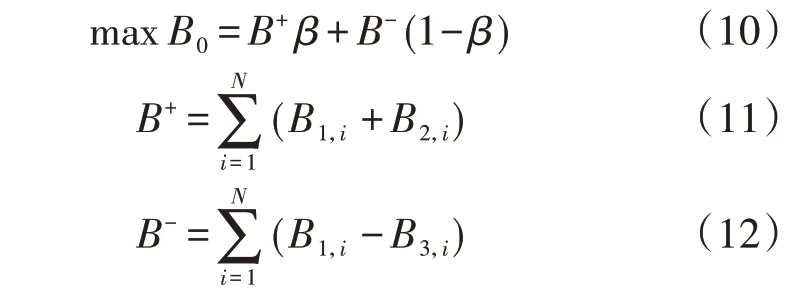
式中:B0为梯级水电站总收益;B+和B-分别为超额完成和合同违约时的梯级水电站总收益;β为0-1 变量,其值为1 表示超额发电,为0 表示未完成合约;N为梯级水电站数量。
根据式(5)—(10),梯级水电站发电收益主要取决于当月的总发电量,其计算公式为:
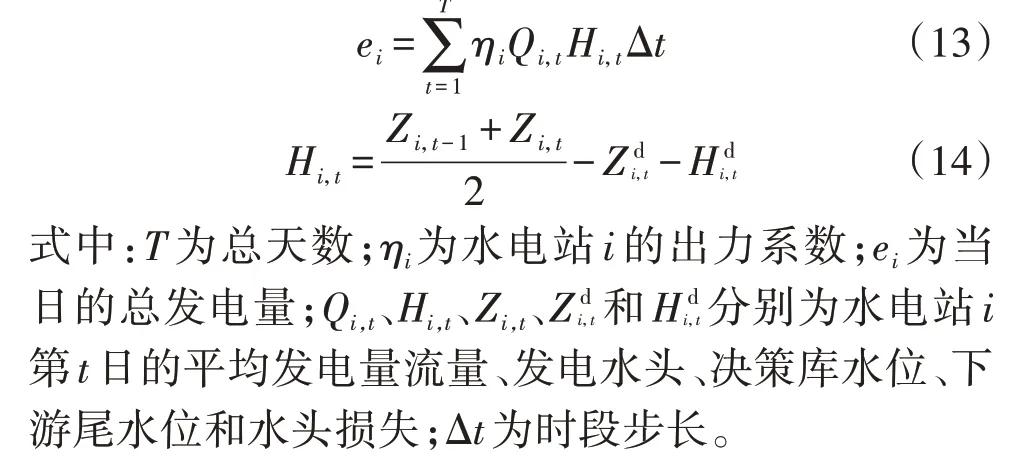
2.2.2 目标函数
本文中水电站的常规水力约束同文献[9],本文仅展示相关的市场化电量约束,具体为:
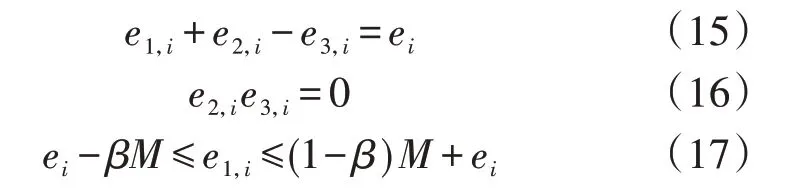
式中:M为足够大的常数。
2.3 基于IGDT鲁棒优化建模及求解
2.3.1 模型建立
为规避日径流、电价不确定性对梯级水电站申报与运行阶段的影响,本文选择IGDT[17]鲁棒模型进行建模,得到中期调度运行阶段满足预期收益时日径流与市场出清电价相较于预测值的最大偏差幅度。与2.2节不同之处如下:


2.3.2 模型求解方法
根据建立的模型可知:模型下层的目标是当不确定变量在[1-α,1+α]范围内波动时,根据收益最大模型计算梯级水电站的市场化收益;模型上层的目标是当市场化收益满足模型预期目标时求解不确定性变量最大偏差范围αˉ,并得到相应的电量申报策略e1,i。分析梯级水电站参与市场交易的目标,根据文献[18]对本文构建的双层模型进行等价转换,转换步骤以及求解流程见文献[19]。
2.4 基于前景理论的中长期市场报价决策模型
2.4.1 模型建立
前景理论认为基于参考点的不同,决策者的决策取决于结果与预期的差距,而非结果本身。鉴于该基本思想,将2.3 节中的Bc=(1-σ)B0作为申报阶段的预期收益,因此梯级水电站售电收益与Bc的心理感知收益偏差ΔB为:
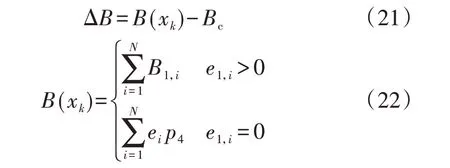
式中:B(xk)为方案k中申报阶段梯级水电站收益函数,分别考虑申报成功和失败2 种情况;p4为水电站的上网电价,为方便计算本文设为统一值。
价值函数体现了梯级水电站决策者对收益偏差ΔB的主观价值感受。当售电收益超过其预期收益,即ΔB>0时,根据价值函数特点,此时决策者是心理“获得”的,具有风险回避的倾向,反之则具有风险偏好的特性。因此,结合式(21)、(22)对价值函数进行改造,具体如下:
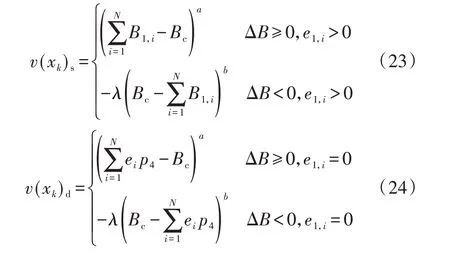
式中:v(xk)s为方案k申报成功时的价值函数;v(xk)d为方案k申报失败时的价值函数。
由于本文市场采取PAB 结算方式,梯级水电站决策者报价越高,申报成功时获得的收益越大,但同时报价越高所面临的申报失败风险越大。因此梯级水电站竞价时需充分考虑其决策方案的风险问题,结合申报成功概率对式(3)、(4)进行改造,具体如下:

根据上述对梯级水电站申报成功和申报失败时的价值函数以及概率权重函数的分析,申报阶段梯级水电站报价决策模型为:
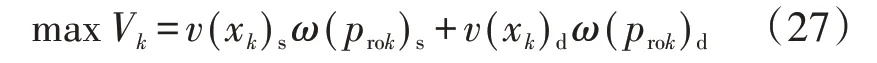
式中:Vk为方案k中的综合前景价值。
2.4.2 模型求解方法
基于前景理论的梯级水电站中长期市场申报阶段报价决策模型的计算流程如附录A 图A1 所示。根据2.4.1节中的目标函数,其求解过程如下。
1)将根据2.3 节中求解得到的预期收益Bc以及满足预期收益时市场出清电价与日径流的变化范围[1-α,1+α]作为前景理论模型的参考点和申报电价的变化范围。
2)选择具有代表性的日径流过程,利用发电量最大模型计算梯级水电站发电量。再由=pmin开始以固定步长增加申报电价,根据式(21)、(22)求出各种报价决策下梯级水电站的收益情况。
3)根据预期收益Bc和式(23)、(24)计算各方案在申报成功和申报失败时的价值函数v(xk)s、v(xk)d,然后根据式(25)、(26)计算各方案在申报成功和申报失败时的概率权重函数ω(prok)s、ω(prok)d,最后得到各方案的前景价值Vk。
4)找到Vk最大的方案,该方案即为梯级水电站最优报价策略。
3 算例分析
本文采用文献[19]中算例。根据实际运行数据,将历史平均值作为预测值,预测的市场出清电价为0.255 3 元/(kW·h),超额完成电价为0.193 58元/(kW·h),违约考核电价为0.2734元/(kW·h),上网电价为0.2元/(kW·h)。各电站的预测入库流量见文献[19],对于径流的不确定性,本文仅考虑龙头水电站A,下游调节性能较弱的水电站的区间径流用多年区间平均径流值进行计算,这是由于枯期梯级水电站发电主要受上游龙头发电流量影响,龙头电站入库流量和下游电站区间径流不是一个数量级水平。
3.1 运行阶段梯级水电站面临风险分析
基于文献[19],将预测电价、预测日径流代入最大收益模型求解调度时梯级水电站参与中长期市场收益最大化问题,得到此时的市场化收益B0=34384.06万元。本文所建模型假定未来实际日径流与市场电价围绕预测值上下波动,波动幅度均为α,根据梯级水电站不同的预期收益目标或风险承受能力σ,可获得鲁棒模型目标αˉ随1-σ的变化如图1所示,计算结果见附录A表A1。
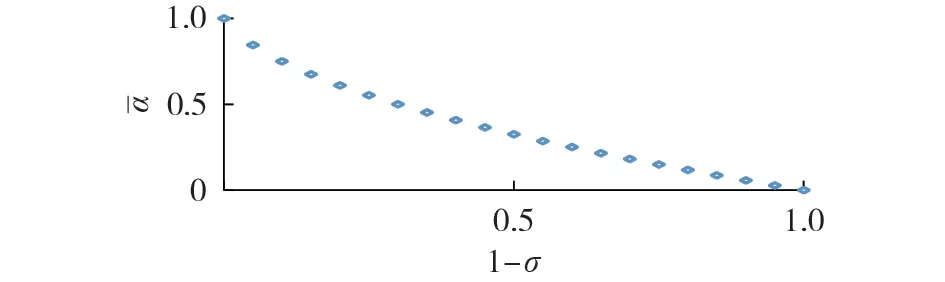
图1 鲁棒模型目标随1-σ的变化Fig.1 Variation of object of robust model along with 1-σ
由图1 可知,随着梯级水电站风险承受能力σ增加,不确定性变量的最大波动范围αˉ也随之增大。即预期收益越低,日径流、电价波动范围越大,得到的电量分配策略鲁棒性越好,越能抵抗较大的日径流波动。
在得到电价与日径流的最大波动范围后,为了方便梯级水电站根据预期收益制定相应的中期运行方案,本文给出鲁棒区域为[1-α,1+α]时梯级水电站的中期水位、出力如附录A图A2所示。图A2(a)、(b)、(c)分别为日径流与电价围绕预测值波动幅度α=0.149 719 时水电站A、B 和C 的运行水位范围,即在该水位范围内运行时,只要电价与日径流的预测误差不超过14.9719%,梯级水电站的市场化收益就不会低于预期收益。因此,决策者可以根据自身的风险偏好,在该范围内制定相应的运行及出力计划,以此优化中期调度方案,规避风险。
3.2 申报阶段梯级水电站申报决策风险分析
基于3.1 节的结果,当1-σ=0.75 时,梯级水电站预期收益Bc=25 788.045 万元,日径流和电价未来实际值相较于预测值的最大波动范围为αˉ=0.149 719,即当未来实际日径流与市场出清电价围绕预测值的波动幅度不超过14.971 9%时,即使是最差情况也能保证梯级水电站的收益至少为25 788.045 万元。根据文献[20]的研究,设定风险偏好系数a=0.88,风险规避系数b=0.88,风险态度系数θ、δ分别取为0.61和0.67,取λ=1.25,对不同的情况进行求解分析。
3.2.1 给定市场化收益下各申报策略的前景价值
给定Bc=25 788.045 万元,市场出清电价的变化范围为[0.2171,0.2935]元/(kW·h),由于电价数据较少,拟合存在较大误差,假设电价在该范围内服从正态分布N(0.255 3,0.016)。日径流设为(1-α)qi,t,此时梯级水电站发电量为1.185 33×109kW·h;固定申报电价步长为0.005元/(kW·h)。计算不同申报策略的前景价值,分别改变电价的均值与方差,再按上述步骤计算相应的前景价值,结果如图2所示。
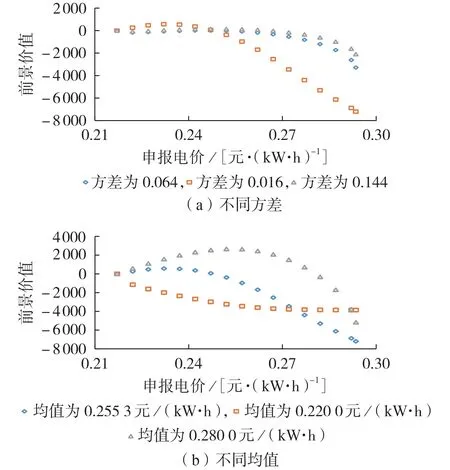
图2 固定预期收益时不同参数下最优决策电价Fig.2 Optimal bidding price under different parameters with fixed expected return
由图2(a)知,方差代表预测电价的波动程度,方差越小代表电价波动程度越小,则电价分布越集中,落在给定区间[1-α,1+α]内的概率越大,而方差越大代表电价波动程度越大,则电价分布越分散,落在给定区间[1-α,1+α]内的概率越小。方差为0.016时,电价分布绝大部分集中在IGDT鲁棒模型给定的区间中,为避免因报价过高不能成交而带来收益损失,梯级水电站最优报价为0.23208元/(kW·h);方差为0.064和0.144时,电价分布在IGDT鲁棒模型给定区间内的比例较小且分散,此时梯级水电站最优报价分别为0.242 08、0.247 08 元/(kW·h),略高于方差为0.016时的电价。由图2(b)知,均值对申报策略的影响大于方差,均值代表预测电价的集中位置,影响申报成功的概率。在IGDT 鲁棒模型给定的电价区间内,均值越接近下界,为了保证申报成功,最优报价也会随之降低,例如均值为0.2200元/(kW·h)时,梯级水电站最优报价为0.21708元/(kW·h),前景价值为负数,代表该申报策略无法达到决策者预期收益,其心理是“损失”的;均值越大,最优申报价格随之增加,例如均值分别为0.2553、0.2800元/(kW·h)时,最优报价分别为0.232 08、0.252 08 元/(kW·h),模型结果符合实际情况。
3.2.2 预期收益变化对申报策略的影响
计算参数同3.2.1 节,改变梯级水电站的预期收益,计算相应的最优报价,如图3所示。
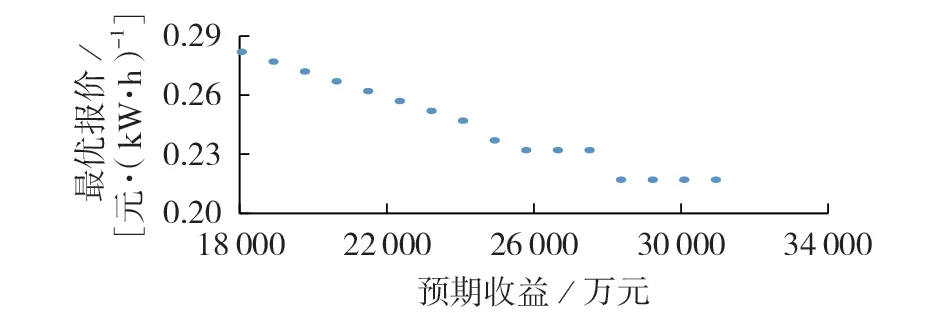
图3 IGDT鲁棒模型中预期收益对最优报价的影响Fig.3 Influence of expected return on optimal bidding price in IGDT robust model
由图3 可知,随着预期收益减小,梯级水电站的最优报价增大,这是由于如果申报失败则梯级水电站所有上网电量均按照上网电价结算,即当预期收益较小时,只需要按照上网电价结算所得售电收益便能够达到梯级水电站的预期收益,因此梯级水电站选择提高申报电价,如果报价成功则能够获得更大利益,即使报价失败也能够通过上网电价保证预期收益。当预期收益大于IGDT 鲁棒模型的预期收益时,最优报价首先保持不变,然后随着预期收益增大陡然下降到电价变化范围的下界。由于1.18533×109kW·h 是梯级水电站在市场出清电价变化范围内鲁棒性最高时的发电量,在发电量不变时,为了达到更高的预期收益需要申报更高的价格。当该价格低于满足IGDT 鲁棒模型预期收益的最优报价0.232 08 元/(kW·h)时,所得利润不能满足梯级水电站的需求,在“损失”的心理下其风险偏好的倾向增加,因此会按照0.23208元/(kW·h)进行申报;当该价格高于0.232 08 元/(kW·h)时,申报失败的概率达到临界点,在给定的电价变化范围内没有满足需求的报价,因此申报电价跳跃到变化范围的下界并保持不变。
3.2.3 申报电量变化对申报策略的影响
当日径流在[(1-α)qi,t,(1+α)qi,t]内变化时,梯级水电站发电量在[1.185 33×109,1.505 23×109]kW·h内变化,其他参数保持不变,计算不同发电量下梯级水电站的最优报价,如图4所示。
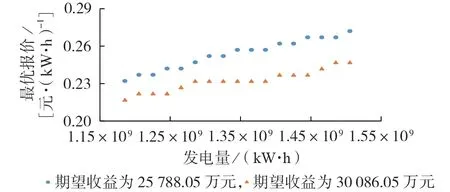
图4 IGDT鲁棒模型中发电量对最优报价的影响Fig.4 Influence of power generation on optimal bidding price in IGDT robust model
由图4 可知,随着发电量的增加,梯级水电站的最优报价逐渐增加,相同发电量下预期收益越大,最优报价越低。当售电收益小于预期收益时,梯级水电站是心理“损失”的,从而有较强的风险偏好倾向,但随着发电量增加,仅靠上网电价结算带来的收益增加,即申报失败带来的“损失”减少,因此梯级水电站愿意选择冒险报一个相对较高的价格以获取更多的利润;当预期收益较大时,相同发电量下申报失败带来的“损失”较大,梯级水电站不愿承担过多的风险,选择报一个相对较低的价格稳定地获得相应的利润。模型很好地体现了梯级水电站的这一心理,与前景理论中“低估大概率事件”和“看重小概率事件”的心理特征相符。
4 结论
本文基于IGDT和前景理论,提出电力市场中联合考虑中长期申报阶段、中期调度运行阶段风险的梯级水电站中期优化调度及交易决策方法,运行阶段优化调度模型概念明确、操作简单、结果直观,能够得到满足梯级水电站预定收益时日径流与市场出清电价相较于预测值的最大偏差幅度。在申报阶段从有限理性的角度出发,考虑决策者对不同收益参考点的风险偏好,比较符合现实情况,在给定电价变化范围内得到最优报价策略。本文得到如下结论。
1)分析电力市场环境下梯级水电站风险时,不能仅依据各方案的总收益,还需要根据决策者的心理参考点来进行评价。因此,梯级水电站运营者的风险偏好程度是影响制定申报策略与运行策略的关键,而且运营者的风险偏好会随着心理预期的变化而变化,存在“低估大概率事件”和“看重小概率事件”的行为特征。
2)利用本文方法得到鲁棒模型中达到梯级水电站不同预期收益目标下中期调度运行方案可抵抗的日径流与电价的波动幅度,然后利用前景理论获得给定预期收益与电价变化范围内的中长期市场最优报价策略,风险回避主体和风险偏好主体可由此评价不同的方案,并采用相应的策略保证预期收益目标。
3)IGDT 方法对不确定因素的信息需求量少,无需获取不确定性参数的概率分布,适用于处理具有严重不确定性的风险决策问题。模型的鲁棒性体现在保证预期目标不低于某个最低预设结果时不确定变量相较于预测值的最大偏离范围。前景理论考虑了决策者的心理,使电价申报决策更加符合实际决策者的行为模式。
附录见本刊网络版(http://www.epae.cn)。

