kagome 晶格中无序和自旋交换作用对量子霍尔电导率的影响

胡凌志,商敬龙,江红民

（宁波大学 物理科学与技术学院,浙江 宁波 315211）

量子霍尔效应是凝聚态物理中在低温和强磁场下一个有趣的电子输运现象.研究人员首先在二维半导体系统中发现了整数量子霍尔效应,随着朗道能级被逐级填满,霍尔电导呈现为等距的阶梯状平台σxy=2ne2/h,n= 0,±1,±2,…,被称作常规量子霍尔效应.随着提取和制备技术的发展,一种以碳原子紧密堆积成单层二维蜂窝状晶格结构的石墨烯材料问世.石墨烯的导带和价带通常在布里渊区的6 个角出现接触点,形成无能隙的半金属,而这些接触点则被称为狄拉克点.同时在接触点处由于能带的线性色散关系,电子的行为由无质量的狄拉克费米子来描述[1].单层石墨烯呈现出一种区别于传统二维半导体的量子霍尔效应σxy= 4(n+1/2)e2/h,n=0,±1,±2,…,通常被称作非常规量子霍尔效应,其中半整数量子化是由于狄拉克点处发生贝利相变π .后来发现的在零磁场中的反常量子霍尔效应,其原因是强的自旋轨道耦合充当了有效Zeeman 场.近些年来,一类具有kagome 晶格结构的二维材料引起了人们极大的研究兴趣[2-15].kagome 晶格是石墨烯蜂巢晶格结构的一个简单变形,其能带结构还保留有蜂巢晶格结构的特征,能带中的两个色散带与石墨烯相同,存在线性色散关系的狄拉克带.另一方面,kagome晶格是一种由对顶三角格子组成的特殊结构,并导致kagome 晶格体系除了两个色散能带之外,还存在一个几乎无色散的平带,同时,对顶三角格子的特殊结构在电子间存在相互作用时表现出强的几何阻挫效应.因此,kagome 晶格结构材料是同时研究狄拉克能带、平带和几何阻挫效应的一个绝佳体系.

在量子霍尔效应中,杂质是一个饶有兴趣的科学问题.虽然直到目前仍存在争议,在Laughlin的规范理论中,必要的杂质效应导致的朗道能级展宽是理解量子化霍尔电导的关键因素之一[16],而较强的无序却会破坏霍尔电导平台[17-18].尽管之前已有理论工作对二维电子气和石墨烯中非磁性无序对量子霍尔效应的影响进行过研究[17-18],然而在kagome 晶格体系的量子霍尔效应中,类似的研究特别是方向随机的磁性无序对霍尔电导的影响却少有.不仅如此,近几年一系列具有磁性相互作用的kagome 晶格结构的材料相继被合成和制备出来,其中具有强烈几何阻挫的反铁磁相互作用的kagome 晶格体系被认为是发现量子自旋液体态的理想材料,特别是S=1/2的kagome 晶格海森堡反铁磁模型的基态是否存在能隙的问题,引起了广泛的争论[2-15].因此在kagome 晶格系统中考虑近邻电子之间的交换相互作用对量子霍尔效应的影响不仅是描述实际材料的要求,而且有助于理解和甄别具有磁性相互作用的kagome 晶格材料中有可能呈现的一些新奇量子态.

受此启发,本文利用数值计算研究了无序和海森堡自旋交换相互作用下kagome 晶格中的量子霍尔效应.其中无序包括非磁性杂质和方向随机的磁性杂质,相互作用包括铁磁和反铁磁相互作用.根据已有的研究结果,可以预见在一个强无序的环境下,量子霍尔平台会被破坏.在磁性无序和反铁磁相互作用下,kagome 晶格的量子霍尔效应还会出现一些有趣的变化.

1 理论和方法

在一个二维的平行四边形kagome 晶格体系中研究杂质和交换相互作用对霍尔效应的影响.如图1 所示,体系的大小为N=N x×Ny,其中Nx和Ny代表两条边中格点的个数;A、B 和C 分别代表3 种不同的晶格点;a1和a2是晶格单位矢量;τ1、τ2、τ3和τ4指从B 类格点跃迁至最近邻格点(A 类和C 类格点)的跃迁积分;(ix,iy)代表格点的坐标.对kagome 晶格平面施加一个垂直方向的均匀磁场

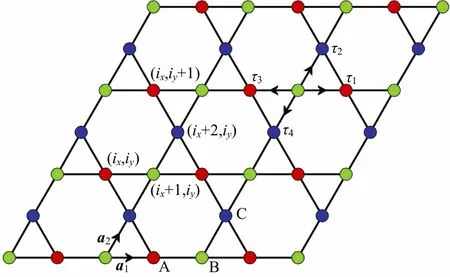
图1 kagome 晶格结构

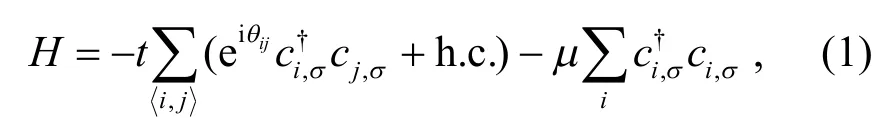
为了研究系统中无序的影响,分别考虑非磁性杂质和方向随机的磁性杂质,杂质的哈密顿量表示为

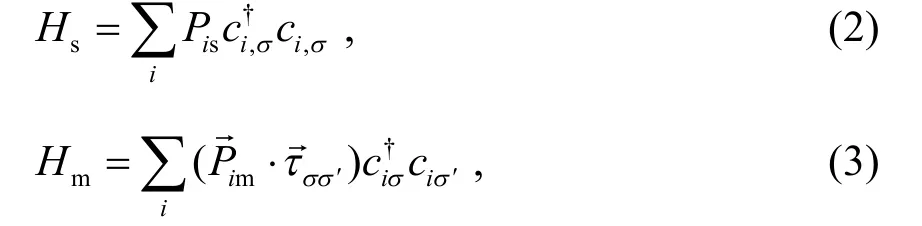
式中:Pis为格点i处非磁性杂质的强度;为格点i处磁性杂质的强度和方向;τσσ′为泡利矩阵.

而近邻电子之间的交换相互作用则可以表示为:

对交换相互作用使用平均场方法,可以得到以下结果:

上述计算中考虑各向同性的情况,其中Jij﹥0表示反铁磁相互作用,Jij﹤ 0为铁磁相互作用.将哈密顿量对角化后,使用Bogoliubov-de Gennes 方程可得:

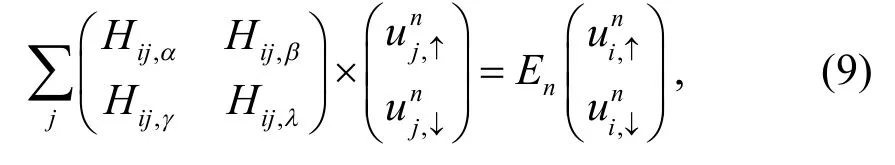
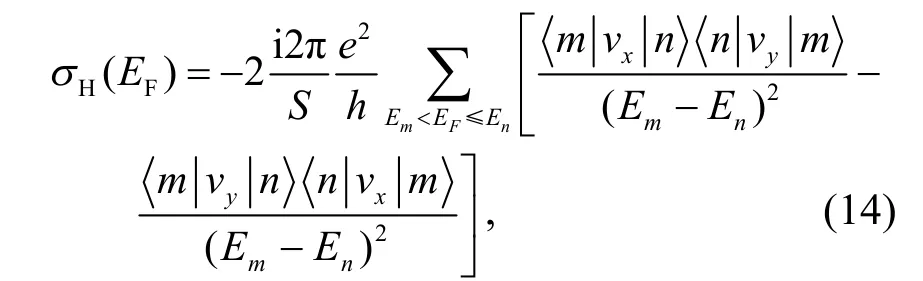
2 结果和讨论

首先计算纯净系统中通过kagome 晶格平面不同磁通量下的量子霍尔效应.图2 所示为M=600、800、1 200 时系统的霍尔电导率,显然该系统的量子霍尔效应与石墨烯晶格中一致,霍尔电导呈现半整数量子化σxy=ve2/h=gs(n+1/ 2)e2/h,n=0,±1,±2,…,上式中简并因子gs=4表示每个朗道能级包含2 个自旋分量和2 个不等价的狄拉克谷点,整数v在图中以数字标示在对应的量子霍尔电导平台上.与二维电子气系统中常规的量子霍尔效应类似,霍尔电导随着费米能EF的变化都呈现为等距的阶梯状,每当一个朗道能级被填满时霍尔电导就增加一个量子数.然而从图中可以发现并不存在σxy=0的平台,这是因为kagome 晶格中的载流子是无质量的狄拉克费米子,其中霍尔电导的半整数量子化是在狄拉克点处贝利相位发生π的突变的结果.随着磁通量的增大,系统的朗道能级随之改变,霍尔电导图中每个平台的宽度也相应地变宽,从图中也能清楚地看到,通过整个晶格平面的磁通量的改变并不影响霍尔电导的量子化特性.

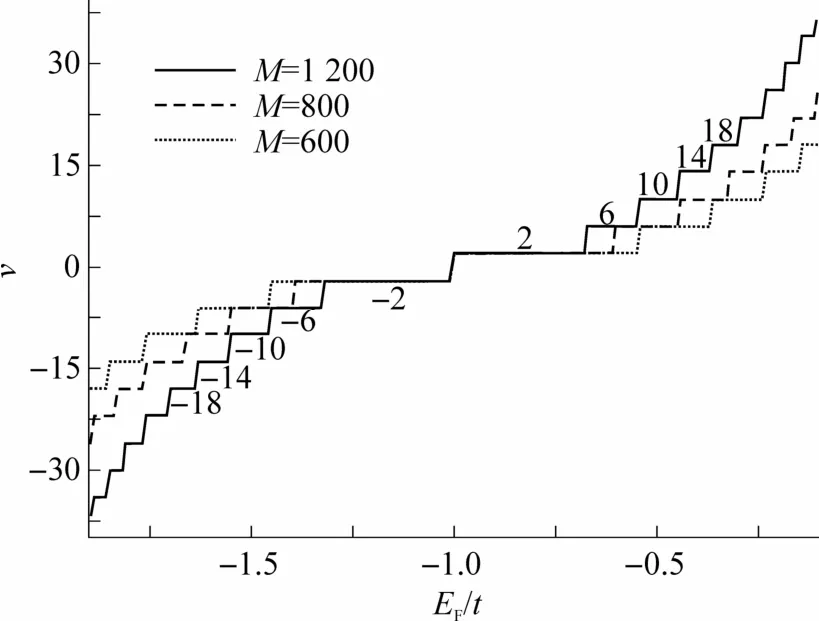
图2 霍尔电导随费米能的变化关系

为了研究kagome 晶格系统中无序对霍尔效应的影响,在系统中随机选取一半格点掺杂大小随机分布在 [ -Ps,Ps]之间的非磁性杂质,于是Ps代表了无序的大小.图3(a)是当M= 1200时,系统中含不同非磁性杂质强度的霍尔电导.图中实线代表Ps=0即系统无杂质的霍尔电导.可以看出,Ps=0.15 时的无序强度相对较低,几乎所有霍尔电导平台都保持着量子化,这表明系统的量子霍尔效应在弱无序状态下是稳定的.当Ps= 0.75时,仅有v=±2,±6,±1 0的平台仍是量子化的.当Ps增加到1.5 时,绝大多数平台都已经被破坏,仅有v= ±2的平台保持完整.可以预测当杂质的强度增大到某一值时,所有的霍尔平台都会被破坏,系统的霍尔效应将不再有量子化的性质.因此,计算结果表明,在kagome 体系中,随着无序强度逐渐增大,霍尔电导从高朗道能级到低朗道能级逐步破坏量子化,对应朗道能级越低的平台具有越稳定的性质,这种无序对量子霍尔效应的影响和石墨烯晶格是一致的.

然而,在包含磁性杂质情况下霍尔电导出现了一些有趣的变化.与系统中含非磁性杂质的研究方法类似,同样在样品中随机选取一半格点加入杂质强度分布在 [-Pm,Pm],方向随机分布在θ∊ [0,π)、φ∊ [0,2π)的磁性杂质,结果如图3(b)所示.图中虚线是Pm= 0.15的霍尔电导随费米能的变化关系,尽管此时无序程度较弱,对原有的霍尔平台几乎没有影响,但在原来相邻的两个平台中间诱导出新的平台,导致体系发生从非常规量子霍尔效应到常规量子霍尔效应的转变.没有杂质时,每个朗道能级En=sign(n)vf具有自旋和狄拉克谷点简并度.当加入磁性杂质时,打破了自旋简并,只剩下狄拉克谷点二重简并度,相应的霍尔电导简并系数从gs=4变为gs=2,同时使得原朗道能→ 级发生劈裂变为Enσ= sign(n)vf×,导致原来相邻的两个平台中间出现新的平台.值得注意的是,最近在反常量子霍尔效应实验中,当局域磁矩随机反转时观察到了类似的非零霍尔电导平台向零霍尔电导平台的转变[19-20],期望以上计算的量子霍尔电导的平台转变能够在掺有磁性杂质的kagome 晶格体系的量子霍尔效应中观察到.当Pm逐步增大时,霍尔电导呈现与图3(a)相似的破坏平台的过程,同时由于自旋劈裂随着Pm增大而相应地增大,v=0的平台宽度也逐步增大.

图3 不同强度非磁性和磁性无序下霍尔电导随费米能的变化关系(M=1 200)

最后计算近邻电子之间的磁性相互作用对量子霍尔效应的影响.图4(a)展示了在铁磁相互作用Jij﹤ 0下体系的霍尔电导率,从图中可以看到,铁磁相互作用使系统由非常规量子霍尔效应转变为常规量子霍尔效应σxy= 2ne2/h,这与图2 纯净系统的非常规霍尔电导形成了鲜明的对比.值得注意的是,在各向异性的kagome 晶格中也有类似的从非常规量子霍尔效应转变为常规量子霍尔效应的现象[21].同时由于在1/3 填充时有零霍尔电导平台的出现,可以知道在铁磁相互作用下体系在1/3填充时存在能隙.对比铁磁相互作用,反铁磁相互作用则对体系的霍尔电导平台没有影响,结果如图4(b)所示,可以看到量子霍尔电导仍是非常规的类型.这个结果意味着在自旋为1/2 的反铁磁交换相互作用形成自旋液体的机制下,体系的量子霍尔效应保持不变,同时也暗示着在自旋为1/2 的反铁磁交换相互作用下,体系和原来系统一样具有零能隙的特征,此特征有助于从实验上探测和研究自旋液体的激发特性和形成机制.

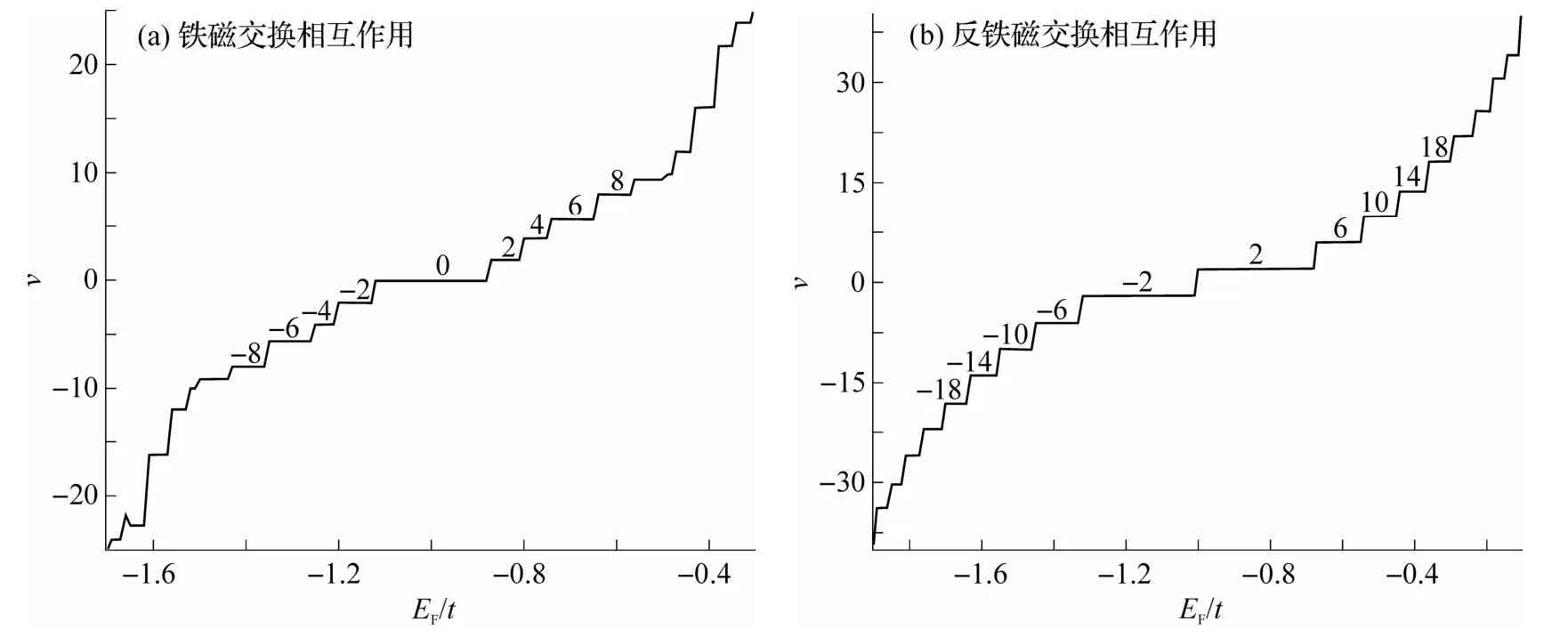
图4 自旋交换耦合作用对霍尔电导的影响(J=0.6)

3 总结

本文计算了非磁性和磁性无序以及海森堡自旋交换作用对kagome 晶格量子霍尔效应的影响.结果表明在纯净的情况下,kagome 晶格呈现出和石墨烯一样的非常规量子霍尔效应.当存在非磁性和磁性无序时,随着无序强度逐渐增大,霍尔电导平台的破坏从高朗道能级对应的平台开始,逐步向低朗道能级对应的平台进行,朗道能级越低的平台表现出越稳定的特性.磁性杂质除了破坏霍尔电导平台外还可以解除自旋简并,使系统发生从非常规量子霍尔效应到常规量子霍尔效应的转变.在近邻电子之间的铁磁性相互作用下,同样能使体系转变为常规的量子霍尔效应,并且由于在1/3 填充时有零霍尔电导平台的出现,表明在铁磁相互作用下体系在1/3 填充时存在能隙.然而在反铁磁相互作用下,体系的霍尔电导仍然是原来的非常规类型.这意味着在S=1/2的反铁磁交换相互作用形成量子自旋液体时,体系仍保持原来的非常规量子霍尔效应,同时也暗示着在S=1/2的反铁磁交换相互作用下,体系和原来的系统一样具有零能隙特征.