含广义k-Horadam 序列的RFPrLrR 循环矩阵的行列式

雷 林，何承源，邱 涛，李笑丽

（西华大学理学院，四川 成都 610039）

矩阵及其行列式在基础数学和应用数学领域占有重要地位[1]，如空间向量[2]、求解线性方程组[3]、曲线的旋转变换[4]、控制理论[5]等问题都可转化为矩阵或行列式的问题。其中，循环矩阵因其良好的性质和特殊的结构成为近年来诸多学者积极关注和研究的课题之一。循环矩阵广泛的应用于应用数学、现代科技工程和物理等领域，尤其在编码理论、图像处理、求解微分方程、通信工程等方面取得了较好的成果。例如，Tanner 等[6]提出了基于循环矩阵的LDPC 块和卷积码。Sebastain 等[7]解决了随机循环图的布局问题。Liu 等[8]利用矩阵分解和循环矩阵的公式求解偏微分方程。在文献[9−11] 中，作者对基于循环矩阵安全性的压缩感知(CS)框架进行了扩展。

由于循环矩阵的重要应用，一些学者不断提出新的循环矩阵，并对其理论性质，行列式、范数、逆、广义逆、循环线性系统等问题进行研究且取得了较好的成果。如，Zheng 等[12−13]研究了求解循环矩阵逆的一个快速GPU 算法。He 等[14]给出了6 种判别H-循环矩阵的方法，并讨论了这类循环矩阵的非奇异性和对角化。Jiang 等[15]给出了含有Perrin、Padovan、Tribonacci 和广义Lucas 数列的RFMLR循环矩阵行列式的精确表达式。Bozkurt 等[16]给出了一些和数字序列相关的r-循环矩阵的行列式与逆。在文献[17]中，作者对含Fibonacci、Lucas、Pell 和Pell-Lucas 数列的RFPrLrR和RLPrFrL循环矩阵的行列式进行了研究。文献[18]得到了一些含有三阶序列的RSFPLR和RSLPFL循环矩阵的行列式。师白娟[19]讨论了带有广义Fibonacci 多项式的循环矩阵的行列式。考虑到二阶多项式和递推序列的多样性，本文主要针对RFPrLrR和RLPrFrL循环矩阵，利用循环矩阵及特殊序列的结构性质和多项式因式分解的逆变换，给出了含广义k-Horadam 序列的这两类矩阵的行列式。由于广义k-Horadam 序列形式的一般性，本文得到的结论将包含所有带有常见二阶递推序列或多项式的RFPrLrR和RLPrFrL循环矩阵的行列式，如文献[17]中含Fibonacci、Lucas、Pell 和Pell-Lucas 数列的RFPrLrR和RLPrFrL循环矩阵的行列式。

为方便起见，本文仅研究复数域上的方阵，并规定 R、In、d etA分别表示实数域、n阶单位矩阵、A的 行列式。

1 预备知识

定义1[17]若n×n矩阵具有形式

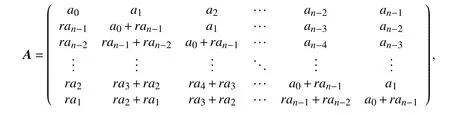
则A为RFPrLrR循环矩阵，表示为A=RFPrLRcircr fr(a0,a1,···,an−1)。

定义2[17]设 π为基本RFPrLrR循环矩阵，则 π有下列形式

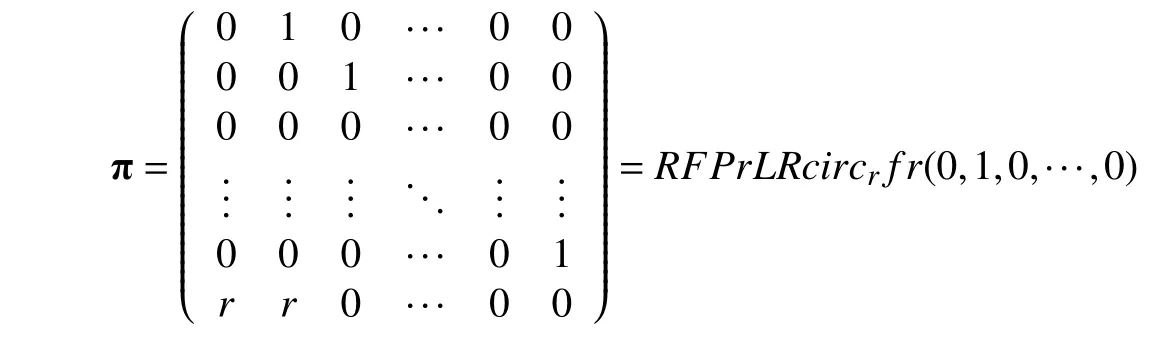
g(x)=xn−rx−r为 π 的特征多项式，在复数域上有n个不同的根，定义为ωj(j=0,1,···,n−1)。此外，π满足πn=rIn+π，并规定π0=In。

若RFPrLrR循环矩阵A=RFPrLRcircr fr(a0,a1,···,an−1)，则A可 表示为

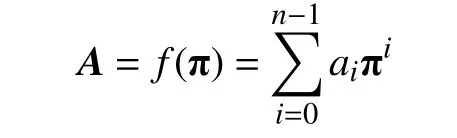
其中f(x)=是A的表示多项式。

定义3[17]若n×n矩阵具有形式

其中n是任意正整数，且f2(k)+4g(k)>0。

广义k-Horadam 序列是常见二阶递推序列或多项式的一般形式。如，当f(k)=k,g(k)=1,p=0,q=1时，我们得到k-Fibonacci 序列 {Fk,n} ；当f(k)=g(k)=1,p=2,q=1时，我们得到Lucas 数列 {Ln} ；当f(k)=2,g(k)=1,p=0,q=1时，我们可以得到Pell 数列 {Pn}；当f(k)=2,g(k)=1,p=2,q=2时，得到Pell-Lucas 数列{Qn}；当f(k)=1,g(k)=2,p=0,q=1时，得到Jacobsthal 数列 {Jn} ;当f(k)=2x,g(k)=−1,p=1,q=x时，得到第一类Chebyshev 多项式 {Tn(x)}。因此对等式(4)中的f(k),g(k),p,q取适当的值，就可得到常见的二阶递推序列或多项式。

{Hk,n}的Binet 公式为

其中X=q−pβ，Y=q−pα 且α,β=是特征多项式x2−f(k)x−g(k)=0的两个不同的根。

2 主要结论

定理1设C=RFPrLRcircr fr(Hk,0,Hk,1,···,Hk,n−1)，则

3 数值例子

例：设4 阶RFPrLrR循环矩阵F=RFPLRcirc1fr(0,1,1,2)，求矩阵F的行列式。

解:由F=RFPLRcirc1fr(0,1,1,2)，可知该循环矩阵的第一行元素满足Fibonacci 数列 {Fn}。设F=RFPLRcirc1fr(F0,F1,F2,F3)，则由推论3，当k=1 时有