高原风力机与来流湍流的多尺度结构响应关系

杨从新，王 强，李寿图，丁佰岑，曹宗彪

（1.兰州理工大学能源与动力工程学院，甘肃 兰州 730050；2.甘肃省风力机工程技术研究中心，甘肃 兰州 730050；3.兰州长信电力设备有限责任公司，甘肃 兰州 730050）

大气边界层复杂的时空特征是导致风力机经历不必要瞬态效应的驱动机制[1]。随着风力机风轮直径的增加，湍流驱动的力对风轮叶片[2−4]等关键部件的载荷产生重要影响。同时，复杂的环境条件使得来流风况发生显著变化，导致机组发生短期和长期的功率波动，影响风力发电的调度能力[5]。其中，文献[6]研究了大气风场极端事件与风轮叶片和主轴上载荷交变的相关性。文献[7]研究表明了风力波动具有较强的间歇统计性。文献[8—9]对不同来流条件下叶片和风轮荷载的变化进行了系统的研究，结果显示了剪切来流和低空急流对荷载有不同的影响。

湍流与风力机具有复杂的相互作用。文献[10]的研究表明，真实条件下风力机的功率输出谱分布是由来流的谱以非线性方式调制的。文献[11]利用湍流谱结构模拟风电场与电力系统的动态相互作用。虽然对风力机和风力发电场对大气边界层的响应的认识已经有了显著的提高，但是对于风力机和湍流之间的相互作用的基本理解较少，还需要从统计方面来更详细地表征风力机的负荷。此外，ABL 中的其他相关现象，如间歇性事件，需要纳入到整体问题中。为此，需进一步认识不同尺度的能量、周期、间歇和其他事件对风力机的相对贡献，以此为改进风力机控制策略等提供参考依据。

为了解在高原环境下的大型风力机功率输出和来流湍流之间的尺度关系，本文在上述研究的基础上，以青藏高原地区为例，基于机舱式激光雷达和机组数据采集与监控(SCADA)系统，利用小波分析方法来获取现场实测的湍流与机组风轮相互作用的信息。

1 现场实验

1.1 实验设备及设置

现场实验在青海省都兰县某风电场进行。实验设备包括一台3.3 MW 的变速变桨型大型水平轴风力机和一台机舱式激光雷达ZephiRDM[12]。风力机的风轮直径D=146 m，轮毂中心高度H=100 m，当风速接近10 m·s−1时可达到额定功率。激光雷达ZephiRDM 位于风力机机舱顶位置，如图1 所示。测点位置距离风轮正前方219 m 处，测量高度与轮毂中心等高，即Z=100 m。雷达与机组SCADA 系统关联统一的时间戳。本实验测量阶段的风向为盛行风向，相对于风轮轴向的风向角分布如图2 所示。在该风向时，实验机组前方近2.5 km 内无任何遮挡。

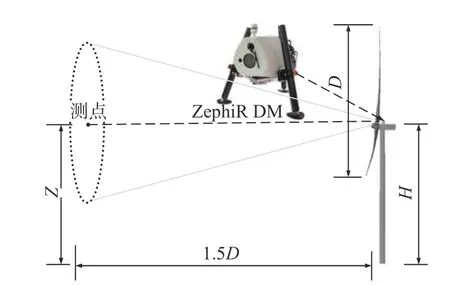
图1 外场实验示意图

图2 风向角概率分布图

1.2 分析方法

小波变换能够消除信号的非平稳性，也能够从信号中描绘尖锐的边缘或不连续点，是湍流分析的常用工具。本文用于表征间歇波动的统计特征。结构函数表示不同尺度和位置的局部波动，本文中用于推断所考虑信号的间歇性特性。

1.2.1 小波函数

有限信号f(t)的连续小波变换Wf(s,b)定义为它与小波ψs,b(t)的标量积：

式中，s和b是函数的尺度参数和位置参数，当s=1,b=0 时称为母小波。本文使用具有高阶矩的Mexican Hat 小波[13]，即

互协方差函数用于确定两个信号f和g跨尺度的相互作用[14]，被定义为

式中τ代表时滞。与标准协方差一样，小波互相关系数ρf,g(s,τ)可以通过适当的归一化得到[15]。

1.2.2 结构函数

信号f(t)在不同尺度s和位置b的局部波动，即δf(s,b)，可以由Wf(s,b)直接得到。它可以更好地表示尺度的相关波动[16]。

将波动δf(s，b)的第m阶统计矩的函数S(m，s)表示如下:

取对数后可推导出其标度斜率τ(m)，即S(m,s)∝sτ(m)。

若m阶统计矩和尺度s之间的双对数呈线性则意味着τ与m之间存在线性的标度指数，即τ(m)=m×H，其中H是Hurst 或标度指数。若此双对数呈非线性关系，则表明了信号的一个多尺度过程，即各种强度的波动在信号中是不均匀地分布。当τ表现出非线性行为时，它可以用二阶多项式近似，如下所示:

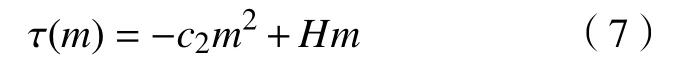
式中，参数c2为间歇性系数，表示对简单尺度的偏离。

2 结果与分析

2.1 数据筛选

本文选取的时间序列遵循平稳性原则，可通过Dickey-Fuller 单位根检验确定。另外，为减少数据的影响因素，选取风向变化最小的盛行风向，并且测量持续时间尽可能长。

为此，选取时间跨度1 h，即2018 年12 月31 日22:30:00 至2018 年12 月31 日23:30:00 的数据。在此时间段，同步采集了风力机的来流风速和输出功率，经无量纲化处理后的时间序列如图3所示。其中机组测点的小时级平均来流风速v=4.683 m·s−1。将以上数据以1 200 s 为周期分为3 段，统计各段来流的平均风速、湍流强度和风剪切指数，如表1 所示。其中段1 和段2 具有相同的平均风速，而3 个时间段内，湍流强度和风剪切指数是增加的，并且剪切指数增加幅度更大。

图3 来流风速与功率时间序列

表1 来流特性

2.2 风力机功率与来流的多尺度结构

在整个采样周期内功率和轴向风速变化显著（见图3），明显看到功率的大范围波动相比风速具有时滞性。这种滞后约为200 s，近似于轮毂高度处测点与风轮的平均对流时间τc(τc=L/v=46.7 s，其中L是雷达测点与风轮之间的距离，L=1.5D)的5 倍。

经归一化的功率与风速的尺度互相关系数为ρP,v(Δ,τ)，其中Δ 是长度尺度，与文献[10]中功率谱密度函数的横坐标频率类似，表示存在对应尺度（频率）的湍流涡结构。二者可以相互转换，尺度越大，频率越低；尺度越小，频率越高。在每个尺度上，可以求得速度与功率之间的最大相关系数(max{ρP,v(Δ,τ)})。如图4 所示，对尺度小于1 的湍流运动影响忽略不计，其中黑色曲线的数据时间跨度是3 600 s，即1 h 的全部数据，而灰色曲线的时间跨度是1 200 s，即选取了其中一段的数据。从整个尺度范围看，沿风轮轴向的来流速度分量与机组输出功率的最大相关系数随长度尺度呈增加趋势，尺度越小，相关系数越低。这意味着风力机的输出功率与来流湍流中具有小尺度的涡结构无关或弱相关。相反，当长度尺度越大，相关系数越接近于1，表明风力机输出功率与来流湍流中具有大尺度涡结构的相关性显著。另外，数据长度会限制长度尺度的范围。

图4 尺度相关系数

图5 是不同长度尺度下计算的最大相关系数对应的尺度时滞变化曲线。为了定量评估与测点到风轮间的平均对流的关系，在垂直轴上显示的时滞长度是经对流时间τc进行无量纲化的。由图可知，不同数据量的尺度时滞随长度尺度的变化不一样，但共同特征是：在小尺度范围，迟滞时间小；中尺度附近（椭圆区域），尺度时滞τ与τc之间存在近似5 倍的关系；大尺度范围迟滞时间又减小。在中尺度存在的倍数关系表明来流湍流中包含该尺度范围的涡结构运动速度比来流风速的平均速度慢。同时，该倍数关系与图3 的时间序列中观察到的功率的延迟时间与对流时间的比值相近似。因此，可以说来流湍流的中尺度涡结构运动是影响风力机输出功率相对来流风速存在的迟滞现象的主要原因。

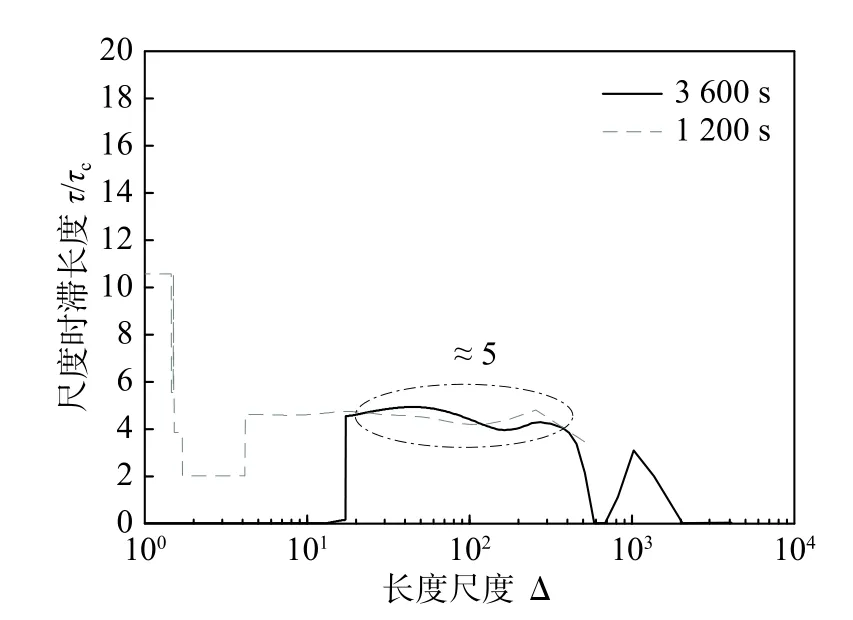
图5 尺度时滞

2.3 风力机功率与来流的间歇性关系

大气边界层中存在的间歇性和高能阵风会对风力机产生非周期性的载荷和非定常效应。根据式(6)，图6(a)和图6(b)分别显示了阶数m从1 到6 时速度Sv(m,s)和功率SP(m,s)信号分别作为尺度s的相关结构函数。由图可见，与功率相比，速度波动中的斜率τ更高。斜率与阶数的关系如图7所示。可见，本实验中速度和功率输出信号的斜率τ表现出非线性行为，可通过式(7)中二阶多项式近似。由图可知，脉动速度和功率都表明这些量之间存在不同程度的间歇行为。具体而言，图7 表明了脉动风速和功率的间歇性，间歇性系数分别为c2=0.047 4 和c2=0.050 6。可见，湍流风速将自身的间歇性传递给了功率，使得功率与湍流风速有相同的间歇行为。

图6 来流风速和功率的统计矩

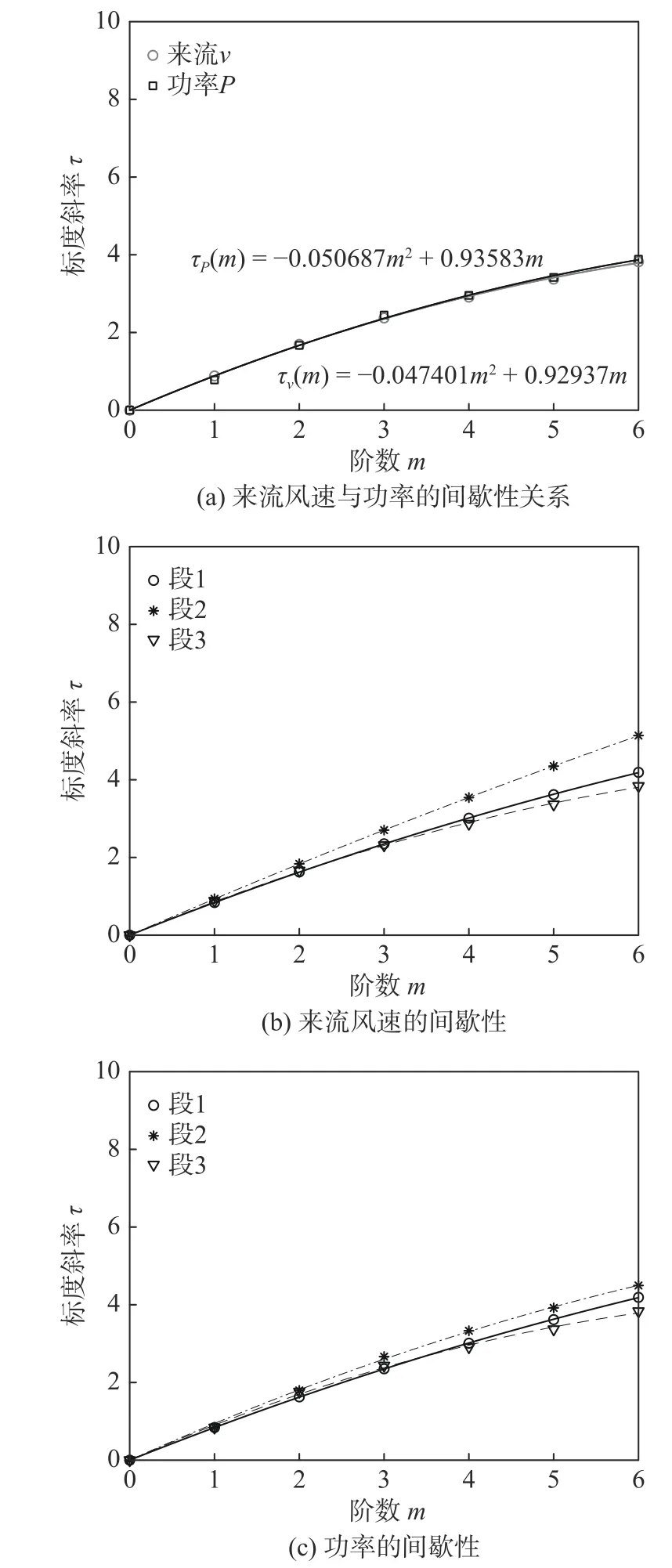
图7 来流和功率的间歇性特征

由表1 可知，选取的时间周期内各段存在不同的湍流强度和风剪切指数。其中湍流强度是指在一个时间段内测点位置的风速随时间的脉动程度，而风剪切指数是指风速沿垂直高度方向上的变化程度，本文中用指数律函数表示风剪切。因此，风速的这种时空变化可能会对机组输出功率和来流的间歇性产生不同的影响。为此，图7(b)和图7(c)分别给出了风速和功率在3 种不同湍流强度和风剪切指数的间歇性关系。由图可见，随着来流条件的改变，风速和功率波动的间歇性发生显著改变。具体而言，相同数据段中，功率的间歇性与风速的间歇性程度相似；随着湍流强度和风剪切指数的增加（段1 和段2），来流的间歇性特征分别被放大，导致输出功率的高度间歇性；另外，段3 的功率和速度的标度斜率要比段1 和段2 的低。因此，风速大小也会对间歇性产生影响。

2.4 风力机功率与来流的谱特性

风力机来流风速和功率时间序列的功率谱密度揭示了各种湍流尺度的重要特征和独特作用。图8 给出了机组沿轴向的来流风速和输出功率的功率谱密度函数，其中光顺的蓝色曲线是依据IEC61400-1 标准绘制的冯卡门谱(VKM)，以突出其总体趋势。但是，与快速傅里叶变换（FFT）得到的实际风速谱相比，IECVKM 在低频区（f<10−1）吻合较好，而在高频区（f>10−1）能量值偏低，而出现这种偏差的原因可能是IECVKM 对高原的湍流风谱不具有普适性。

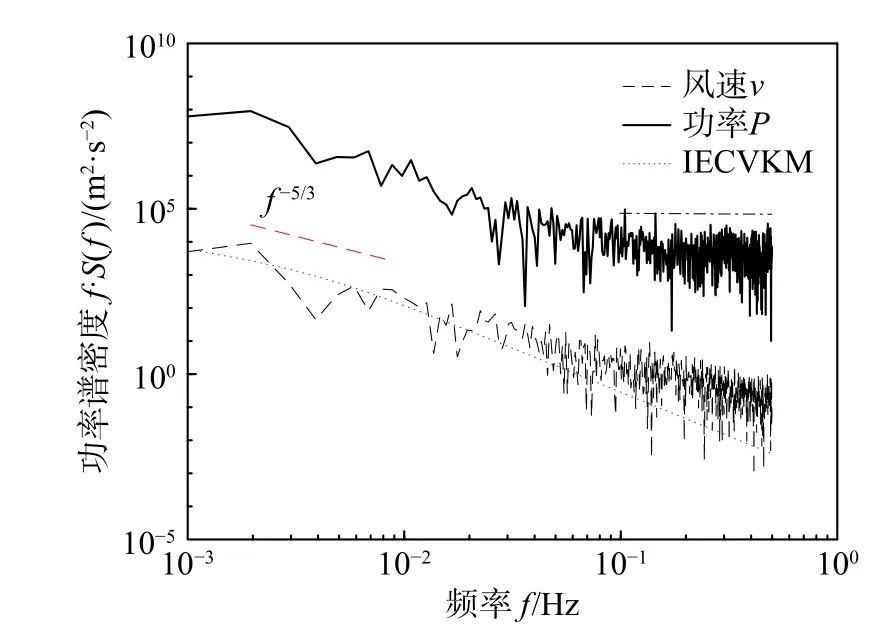
图8 功率谱密度函数

对于机组的输出功率，低频区能量衰减与风速有相同的趋势，均存在斜率为−5/3 的Kolmogorov惯性子区间，表明功率在低频区与大气湍流具有相同的动力学特性。而在高频区，功率的能量值呈现近似水平趋势，表明功率在高频区与大气湍流无关。这与文献[10]结果类似。

3 结论

本文利用激光雷达测量的来流风速和机组SCADA 系统采集的风力机功率，研究了在青藏高原环境下的大型水平轴风力机的尺度相关性，利用小波分析等方法计算和量化了来流和功率尺度相关性和间歇性行为，得到以下结论。

1)当湍流尺度介于中尺度范围，尺度时滞与对流时间呈近似5 倍关系，近似于功率相对来流风速的延迟时间。

2)标度斜率的二次模型表明，来流的间歇性特征被传递到风力机风轮上，导致输出功率的高度间歇性，传递到输出功率的间歇性程度因来流条件不同而发生改变。

3)功率在低频区与风速有相同的动力学特性，高频区与风速无关。

4)本实验选取样本数据相对较少，后续通过增加样本数据和筛选平均风速、湍流强度以及风剪切指数等参数作为单一变量对来流湍流与输出功率相关性做深入研究。