基于拉格朗日插值法的国省干线缺失数据恢复

赵媛媛 季洁

摘 要：针对国省干线公路采集的交通数据存在缺失值的情况，文章提出了基于拉格朗日插值法的缺失数据恢复方法。首先，找出缺失数据所在位置以及所属时间段;其次，采集该位置和该时间段的历史平均交通数据;再次，利用拉格朗日插值法对缺失数据进行填补;最后，比较正常数据算出的插补值与真实数据，评价插补的结果。试验结果显示，该方法简单、方便、易实现，可以完成对简单的公路数据缺失值的恢复，确保数据在交通控制、路网规划等应用中的可靠性。

关键词：拉格朗日插值法;缺失值;交通数据

1    研究背景

对国省干线的交通状况进行分析时，需要利用各种先进的交通信息采集技术采集国省干线上的交通数据，并对采集到的数据进行相应的处理和应用，如集成、抽样、压缩、存储、发布等[1]。这些数据中隐含的交通时空分布规律对有关部门在交通控制、路网规划等方面有着较大的参考和利用价值[2]。

然而，由于交通采集设备故障、施工损坏、环境和气象恶劣等因素的存在，会导致所采集到的交通数据有缺失的现象。数据缺失降低了数据的质量，对利用数据进行交通运行状况分析、交通控制、路网规划等均会产生不利的影响。面对海量的交通数据，数据缺失不可避免，因此需要选择合适的方法对缺失数据进行处理，以此来保证数据的质量，保证数据在交通控制、路网规划等方面的可用性。

2    现状分析

目前，常用的缺失值处理方法大致有两种：删除和填充。（1）删除数据即剔除存在缺失的一组数据，从而保证保留的数据是完整的。这种方法简单但需牺牲某些数据属性，而各个数据间存在着一定的关联，直接剔除可能会对数据的分析结果造成不利影响，数据删除不常用于缺失值处理。（2）填充数据即选取合适的数据填补缺失数据，以保证数据集的完整性，利用数据填充的方法可以获得较优质的数据分析结果。针对国省干线交通數据的缺失值，可以借助已采集的正确数据进行异常数据的差值处理，因为拉格朗日差值法有着简单、方便、易实现的优点，所以将其用于国省干线简单缺失数据的恢复可以取得较理想的结果。

拉格朗日插值法广泛应用于各个领域的数据处理，取得了较好的效果。杨皓翔等[4]运用拉格朗日插值法减少了边坡位移监测数据的误差对新陈代谢模型预测精度的影响。丁闪闪等[7]运用平均法和拉格朗日插值法对交通数据采集过程中的异常数据进行修正，结果表明，拉格朗日插值法相较于传统的平均法准确性更高。陈飞等[8]提出了基于拉格朗日插值的方法来实现射频信号衰减的修正，在保证修正数据准确度的前提下既减少了修正的工作量又降低了系统后期维护的难度。秦利刚[9]将拉格朗日插值法运用于频谱分析中，不但克服了因频率漂移造成数据点采样不足的问题，还克服了拉格朗日插值算法在频谱分析中的应用的泄漏问题。蔡文等[9]利用改进型的拉格朗日插值算法改善了视频分割处理图片失真的问题，实验表明改善后的拉格朗日算法即重心拉格朗日算法具有明显优越性。综上所述，拉格朗日插值法在各个领域的数据处理方面均取得了较好的效果，因此，选择拉格朗日插值法恢复国省干线的缺失数据。

3    方法原理

3.1  算法原理

拉格朗日插值法基本原理：在插值点的附近选取若干合适的节点，构造一个简单的插值函数y=p（x），要求构造的插值函数穿过选取的节点。在所选数据区间用插值函数作为原来函数f（x）的值，使得f（xi）=p（xi），i=1，2，3，…，n成立。由此可见，插值法的实质是根据已知的节点数据或线图上某些已知点的数据构造一个既简单又能够保证精度的插值函数p（x），并利用该插值函数快速获取原函数在对应位置的数据，这种利用若干节点来构造插值函数的方法称为拉格朗日插值法[3]。

对于原函数f（x）分别有给定的n+1个取值点，分别为（x0，y0），（x1，y1）， … ，（xn，yn），其中，x对应自变量的位置，y为原函数f（x）在该点的取值。解设任意两个不同的xj都互不相同，以下拉格朗日差值法填补缺失值的步骤。

第一步：求已知n+1个点对的拉格朗日基本多项式lj（x）（或称插值基函数）。其表达式为：

拉格朗日基本多项式lj（x）的特点是在xj上取值为1，在其他的点xi（i ≠j）上取值为0。

第二步：求已知n+1个点对的拉格朗日差值多项式L（x）。其表达式为：

第三步：将缺失的函数值对应的点代入插值多项式得到缺失值的近似值L（x），完成缺失数据的填补任务。

3.2  算法流程

面对海量的交通数据，利用拉格朗日插值法进行缺失值填补需要借助于计算机，其具体算法流程如图1所示。

3.3  拉格朗日插值法在国省干线缺失值中的使用

在面对公路的交通数据缺失时，拉格朗日插值法的具体使用步骤如下：

第一步，确定缺失数据所在的位置（路段）以及缺失情况。

第二步，确定缺失数据对应的时间段。

第三步，根据缺失数据的特征，采集缺失数据对应的指定时间段（点）和路段的历史（平均）交通数据。

第四步，利用拉格朗日插值法填补缺失值，先构造拉格朗日多项式，对指定数据进行插值。其中，指定路段、时间段（点）作为自变量xi，历史（平均）交通数据作为因变量即插值函数值f（xi）。

第五步，验证插值效果：取正常数据作为测试集，对测试集采用相同的方法进行插值，结合真实数据，对测试集的插值进行误差检测，评价插值效果。选取均方误差（MSE）、均方根误差（RMSE）以及平均绝对百分比误差（MAPE）作为评价指标。误差越小，插值效果越好，反之亦然。以下为各评价指标的含义。

均方误差MSE（Mean Square Error）：

均方根误差RMSE（Root Mean Square Error）：

平均绝对百分比误差MAPE（Mean Absolute Percentage Error）：

其中，yi表示真实值，表示预测值，n表示样本容量。

4    实例分析

为验证拉格朗日插值法对缺失值修复的效果，从完整无缺失的路段中随机选取部分值作为缺失数据，采用拉格朗日插值法进行数据恢复，并对所得结果与实际值进行比较。

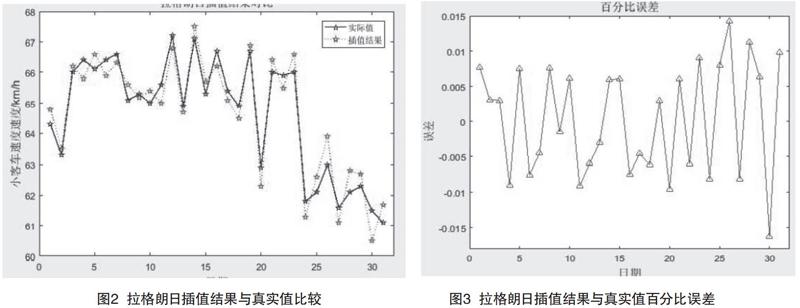
本文选取了南京G235东坝下行段全月数据为例进行说明，将每日中午12时的小客车速度作为缺失值，利用其余时段速度的已知值对该值进行修复，得到的结果如图2—3所示，总体误差指标如表1所示。

结果表明，拉格朗日插值结果与真实值的均方误差在可接受范围内，平均绝对百分比误差小，拉格朗日插值法在缺失数据恢复工作中效果较好。

5    结语

文章基于拉格朗日插值法对国省干线的交通数据缺失值进行填补，并结合具体实例验证了拉格朗日插值法对于缺失值填补的有效性。对于一些简单的缺失值，拉格朗日插值法简单、方便、易实现，且拉格朗日插值法公式的结构整齐紧密，为理论研究提供了便利。利用拉格朗日插值法填充国省干线交通数据的缺失值，可以提高数据的质量，也确保了数据在交通控制、路网规划等应用中的可靠性。

[参考文献]

[1]耿彦斌，于雷，赵慧.ITS数据质量控制技术及应用研究[J].中国安全科学学报，2005（1）：82-87.

[2]韩卫国，王劲峰，胡建军.交通流量数据缺失值的插补方法[J].交通与计算机，2005（1）：39-42.

[3]林昌华，杨岩.拉格朗日插值法在工程设计及CAD中的应用[J].重庆理工大学学报。2013（12）：34-37.

[4]杨皓翔.基于拉格朗日插值法的新陈代谢模型在边坡位移监测中的应用[J].安全与环境工程，2017（2）：33-38.

[5]胡玄子，陈小雪.数据处理中缺失数据填充方法的研究[J].湖北工业大学学报，2013（5）：82-84.

[6]徐小丽.拉格朗日插值法在工程应用中的算法实现[J].林区教学，2010（1）：17-19.

[7]丁闪闪，季锦章.基于小波分析和拉格朗日的交通异常数据处理[J].公路与汽运，2015（169）：59-63.

[8]陈飞，朱坤，贾建兵，等.基于拉格朗日插值法的ATS射频信号衰减修正研究[J].海军航空工程学院学报，2018（1）：45-48.

[9]秦利剛.拉格朗日插值算法在频谱分析中的应用[J].电子世界，2014（5）：112.

[10]蔡文，吴黎明.改进型的拉格朗日插值在视频分割处理的实现[J].自动化与信息工程，2014（2）：29-32.

[11]HE R，ZHANG L W，HE X X.Interval recognition algorithm of the pavement surface condition based on lagrange interpolation method[J].Mathematical Problems in Engineering，2020（1）：1-8.

（编辑 姚 鑫）