基于苏拉卡尔塔棋的差分学习算法研究

李森潭 刘超富 李宇轩 张楚仪 李若溪

摘 要：文章结合深度神经网络与差分学习，在苏拉卡尔塔棋博弈中引入人工神经元为棋子的移动估值，并结合差分学习得到最有价值的棋子移动。神经网络的输入为棋局，输出为棋子的价值估计，之后用它们来指导即时差分学习（TD）。每出现一个局面，使用??贪婪法来选择新的动作和更新价值函数，从而使博弈效果越来越好。

关键词：神经网络;差分学习;损失函数

0 引言

棋类博弈游戏具有智能性，所以在人工智能界很早就被重视，被称为人工智能的“果蝇”。从战胜世界棋王卡斯帕罗夫的国际象棋深蓝到战胜李世石的围棋博弈程序 AlphaGo，计算机博弈再次引起业内的广泛关注。截至目前，国内已经顺利举办了十四届全国大学生计算机博弈大赛，苏拉卡尔塔棋是其中的一项比赛项目。

近年来，许多学者引入机器学习和强化学习对计算机博弈进行优化。主要搜索方法包括：差分学习、阿尔法贝塔剪枝和蒙特卡洛树等，都在一些棋类中有其成功的应用。

本文介绍了机器学习，强化学习与苏拉卡尔塔棋机器博弈的阶段性成果，该方法主要是结合深度神经网络与差分学习，在苏拉卡尔塔棋博弈中引入人工神经元为棋子的移动估值，并通过差分学习修改网络参数，从而得到最有价值的棋子移动。神经网络的输入为棋局，输出为棋子的价值估计，之后用它们来指导即时差分学习（TD）。每出现一个局面，使用??贪婪法来选择新的动作和更新价值函数，从而使博弈效果越来越好[1]。

1   苏拉卡尔塔棋简介

苏拉卡尔塔棋是一种双人游戏[2]，源自印尼爪哇岛的苏拉卡尔塔（Surakarta）。横竖各6条边构成正方形棋盘，36个交叉点为棋位，各边由8段圆弧连接，通常用2种不同颜色表示。游戏在开始时，每一方有12个棋子各排成2行。棋盘如图1所示。

规则如下：

（1）参与者掷硬币决定谁先开始。一次只能移动一个棋子。两个棋手轮流下棋。

（2）如果移动方向没有棋子，任何棋子都可以在8个方向（上、下、左、右、左上、左下、右上、右下）移动1个格。

（3）如果你想吃掉对方的棋子，必须水平和垂直地走，并且至少穿过一条与路径相切的弧线，移动的路径不能被自己的棋子阻塞。

（4）黑子可以吃掉红子，红色也可以吃掉同一路径相反方向的黑子。

（5）当一个界面上的一方所有棋子都被吃掉时，游戏结束，有剩余棋子方获胜。

（6）计算机博弈一般说来，如果每局持續时间超过30分钟，双方都会停止，以剩余更多的棋子方赢得比赛。

2 苏拉卡尔塔棋棋盘分析和程序实现

2.1  棋盘和棋子分析及表示

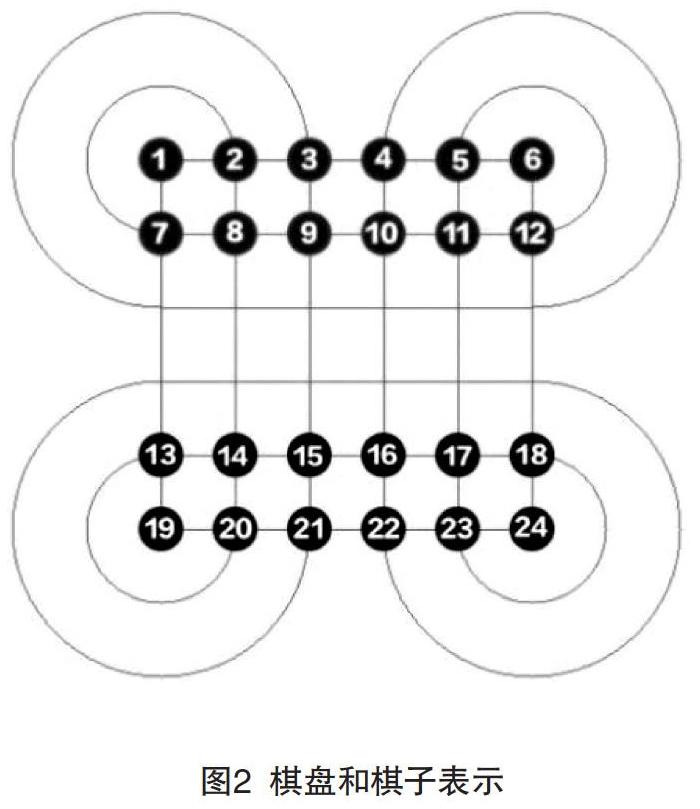
（1）棋盘每个点以坐标的形式表示，左上角的点为坐标原点，1号红棋子坐标为（0，0），2号红棋子坐标为（0，1）， 7号红棋子坐标为（1，0），如图2所示。

（2）棋子双方分别为红和蓝色区分，每一个棋子又有各自的编号。

（3）下棋信息记录。对于行棋路径信息，采用字典对表示，字典对的第一个元素记录起始点，第二个元素记录目标点，其数据结构必须满足。

（4）判断是否对局结束。在红黑双方每走一步后，程序通过对棋盘上双方各自的棋子数量进行统计，从而判断出胜负;若双方在行棋时耗时过长，则直接判负。

2.2  程序实现

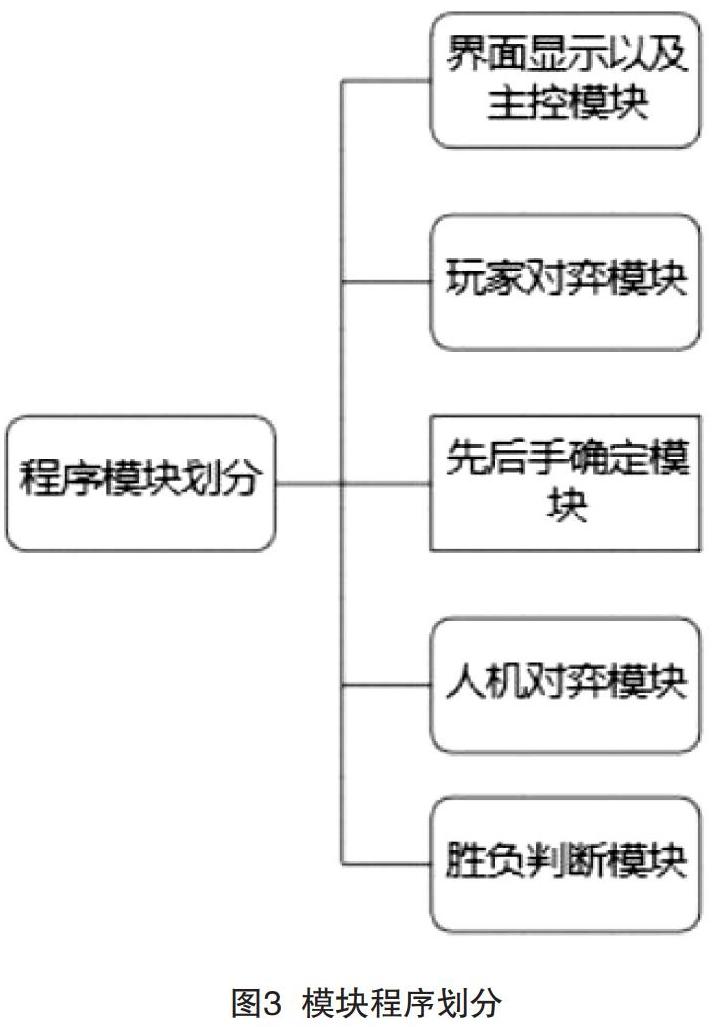
棋类的博弈程序必须要有优良的人机交互体验、良好的界面、快速的棋局计算时间、可供用户自由选择玩家对弈或人机对弈，并能自动判断成绩和记录分数[3-4]。对应功能需求划为图3中的几个模块，程序中重要的人机交互界面划分，如图3—4所示。

3基于搜索树的深度神经网络与差分学习相结合的方法

3.1  基于苏拉卡尔塔棋的深度神经网络的结构特征

机器学习方法与传统方法不同，它只需要将棋盘和历史数据输入到神经网络中，并不用特别特征设计及人工调参[5]。输入网络中的特征，如表1所示。

此外，与五子棋不同，苏拉卡尔塔棋是移动型棋子，即每步把棋子从某个位置移到另一个位置，我们使用一个平面来表示移动棋子的位置，再使用另外一个平面来表示棋子移到的位置。然后，使用一个平面进行表示当前是否为先手方，如果是先手放，则该平面全部置为1，否则全置为0。笔者使用的深度神经网络为6层的卷积残差网络，分为策略网络（见表2）和价值网络（见表3）两个部分。其中，以策略网络作为36×36的输出，表示所有允许的移动。神经网络中的激活函数除已说明外，其余皆为relu函数。

3.2 差分学习

时序差分法（TD）学习是最重要的增强学习方法，其重要目标是：当不受人工干预时，进行自学习训练，从而来进行更新估值函数的权值向量[6]。在计算机博弈的背景下，TD学习可总结为修正权值向量以对估值函数进行拟合的过程。TD利用回报值进行学习，相比于一般的监督学习，TD用差分序列来实现对权值向量的训练，其关键也在于误差可以用一系列预测值之和来表示。TD同时与深度神经网络相结合，能够更好地调整神经网络的参数。此次博弈程序思路基于同策略时间差分sarsa模型展开。

SARSA算法给定强化学习的7个要素：状态集S，动作集A，即时奖励R，衰减因子γ，探索率?，求解最优的动作价值函数q?和最优策略π?，不需要环境的状态转化模型。对于它的控制问题求解，即通过价值函数的更新，来更新当前的策略，再通过新的策略，来产生新的状态和即时奖励，进而更新价值函数。一直进行下去，直到价值函数和策略都收敛[7-8]。

使用??贪婪法来更新价值函数和选择新的动作，即开始时设定一个较小的?值，以1??的概率贪婪地选择目前认为是最大行为价值的行为，而以?的概率随机地从所有m个可选行为中选择行为。用公式可以表示为：

在进行迭代时，先用??贪婪法从当前状态S中选择一个可行动作A，随后转入到一个新的状态S'，此时给出一个即时奖励R，在下一个状态S'中再基于??贪婪法从状态S''中得到一个动作A'用来更新的价值函数，价值函数的更新公式是：

其中，γ是衰减因子，α是迭代步长，收获Gt的表达式是R+γQ（S'，A'）。

当随机初始化神经网络之后，对于每一个棋局状态，可以得到選择的行动的价值估计，同时根据动作A'之后的局面S'，得到v'=fθ（s'）。随后，能够使用反向传播算法对我们所构建的神经网络进行训练。图5—6为同策略差分学习模型。神经网络中以交叉熵和平方差两部分来组成损失函数，即对于棋局中的某一个状态：

x公式中以来作为使L2正则化的参数。

遵循某一策略时，在S，选择一个行为A，与环境交互，得到奖励R，进入S'，再次遵循当前策略，产生一个行为A'，利用Q（S'，A'）更新Q（S，A）。

Every time-step：

Policy evaluation Sarsa，Q∣qm

Policy improvement ? -greedy policy improvement

下面是SARSA算法应用于苏拉卡尔塔棋的流程：   （1）算法输入。迭代轮数T，状态集S，动作集A，步长α，衰减因子γ，探索率?。（2）输出。所有的状态和动作对应的价值Q。①随机初始化所有的状态和动作对应的价值Q。对于终止状态其Q值初始化为0。②for i from 1 to T，进行迭代。

（a）初始化S为当前状态序列的第一个状态。设置A为??贪婪法在当前状态S选择的动作。

（b）在状态S执行当前动作A，得到新状态S'和奖励R。

（c）用??贪婪法在状态S'选择新的动作A'。

（d）更新价值函数Q（S，A）：

Q（S，A）=Q（S，A）+α（R+γQ（S'，A'）?Q（S，A））

（e）S=S'，A=A'。

（f）如果S'是终止状态，当前轮迭代完毕，否则转到步骤（b）。

对于步长α，将随着迭代的进行逐渐变小，这样才能保证动作价值函数Q可以收敛。

同策略时间差分sarsa模型算法为：

Initialize Q（s，a），s∣S，a∣A（s），arbitrarily，and Q（ terminal-state，

Repeat （for each episode）：

Initialize S

Choose A from S using policy derived from Q（e.g.，ε -greedy）

Repeat （for each step of episode）：

Take action A，observe R，S'

Choose A' from S' using policy derived from Q （e.g.，ε -greedy）

until S is terminal

4 实验结果

对实际训练效果进行检验，对深度神经网络进行训练和评估时，将训练时的温度控制常量τ=1，在评估性能时τ= 0.1。对于网络的训练，笔者进行了3 000次的模拟。在评估性能时，笔者用训练500局的神经网络与训练更多次数的神经网络进行了100局对战，双方各模拟了30 s。实验结果，如表4所示。值得注意的是，对于性能的评估，应适当地增加模拟的次数，从而获得更优异的性能表现。

由此可见，当增加训练局数时，深度神经网络的博弈水平不断地提高，所以，使用基于TD的深度神经网络博弈对于提高苏拉卡尔塔程序的博弈水平是可行的。

5 结语

本文是在苏拉卡尔塔棋机器博弈中应用结合深度神经网络与差分学习的方法。在程序自学习训练的过程中，其博弈水平不断地提高。由此可见，如果进行上百万局的自博弈训练，其博弈水平将会到达一个很高的高度。在未来的研究实践中，调整自学习策略、优化网络结构、引入人类对战数据等方面会是我们不断探索的方向。

[参考文献]

[1]桂义勇.一种国际跳棋的博弈系统研究[J].智能计算机与应用，2020（4）：32-34，39.

[2]曾小宁.五子棋中的博弈问题[J].广东第二师范学院学报，2003（2）：96-100.

[3]王坤峰，苟超，段艳杰，等.生成式对抗网络的研究进展与展望[J].自动化学报，2017（3）：321-332.

[4]BERTALMIO M，VESE L，SAPIRO G，et al.Simultaneous structure and texture image inpainting[J].IEEE Transactions on Image Processing，2003（8）：882-889.

[5]COLOMABALLESTER，MARCELO BOL，VICENT C，et al.Filling-in by joint interpolation of vector fields and gray levels[J].IEEE Transactions on Image Processing，2001（8）：1200-1211.

[6]GROSSAUER H.A combined PDE and texture synthesis approach to inpainting[C].Berlin：European Conference on Computer Vision.Springer，2004.

[7]BARNES C，GOLDMAN D B，SHECHTMAN E，et al.The patchmatch randomized matching algorithm for image manipulation[J].Communications of the ACM，2011（11）：103-110.

[8]MIYATO T，KATAOKA T，KOYAMA M，et al.Spectral normalization for generative adversarial networks[J].ArXiv Preprint Arxiv，2018（2）：75-59.

（编辑 姚 鑫）