混凝土内部湿度场与自约束应力场的研究

钟 卓，黄乐鹏，张 恒

(1.中建四局第三建设有限公司，遵义 563099；2.重庆大学土木工程学院，重庆 400044)

0 引 言

钢-混凝土组合剪力墙以及其他结构构件中的混凝土在实际工程中常常处于单面或多面干燥的环境下。与干燥面的距离不同，混凝土内部水分的蒸发速率不同，由此导致混凝土内部湿度的不均匀分布[1]，距离干燥面越近，混凝土内部湿度越低。研究表明，当混凝土中的湿度处于50%～100%时，能通过毛细孔张力理论对混凝土收缩的原因进行解释。毛细孔张力理论认为，混凝土中毛细孔中水分散失，而在毛细孔壁上产生的毛细孔应力则是混凝土收缩的动力来源。混凝土中的毛细孔应力将随着混凝土内部相对湿度的变化而改变，相对湿度越低，毛细孔应力越大，混凝土的收缩也就越大[2-5]。所以，在混凝土内部，不均匀的湿度场将导致混凝土内部产生不均匀收缩变形，使得混凝土内部湿度高、收缩小的部分对内部湿度低、收缩大的部分产生约束，从而使得混凝土在没有外部结构的约束下，也会产生自约束应力。当自约束应力大于混凝土同期的抗拉强度时，混凝土就会产生裂缝。钢-混凝土组合剪力墙内部约束条件(钢板、钢筋及栓钉)十分复杂，混凝土内部由外部约束导致的拉应力进而提高，增加了混凝土开裂的风险。

近些年来，研究者开始重视对混凝土内部湿度及其扩散过程的研究。在众多研究中，主要是通过理论和试验求解基于非线性的湿度扩散方程以及确定非线性方程关键计算参数“混凝土湿度扩散系数”[6-7]。通过测量混凝土中水分随外界条件变化的规律，能够确定混凝土湿度扩散系数，其中通过对扩散方程和湿度测量数据反向求解扩散系数是较为典型的方法。代入湿度扩散方程的数据能真实、稳定地反映混凝土内部水分的扩散能力是该方法的关键之处，这也说明了研究的必要性。本文对混凝土内部湿度场和自约束应力场开展了试验研究，并通过理论推导，建立了混凝土内部湿度、应变与内部湿度关系的理论计算模型。

1 实 验

1.1 配合比

选取28 d抗压强度约40 MPa和80 MPa的混凝土分别代表普通强度混凝土和高强混凝土。两种强度混凝土的配合比如表1所示。

表1 混凝土配合比Table 1 Mix proportion of concrete

水为自来水；水泥为P·O 42.5普通硅酸盐水泥；细骨料为河砂，细度模数为3.1；外加剂为FND缓凝型减水剂，减水率为24%；砾石的粒径范围为5～20 mm，吸水率为2.13%。

1.2 混凝土内部湿度、温度及变形测试

试件采用的模具(见图1)为树脂玻璃，模具内部尺寸为325 mm×100 mm×200 mm(长、宽、高)。同时，在模具底部搁置两片1 mm厚的特氟龙薄片以减少摩擦。

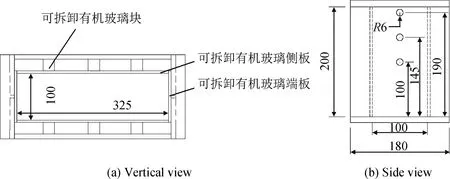
图1 试验所用模具(单位：mm)Fig.1 Experiment mould (unit: mm)

在沿模具长度方向上的两端，距离模具中心0 mm、45 mm、90 mm处分别开直径为12 mm的圆洞，用于安放测量用的螺栓，以便测量混凝土试块沿高度方向上的应变，如图2所示。

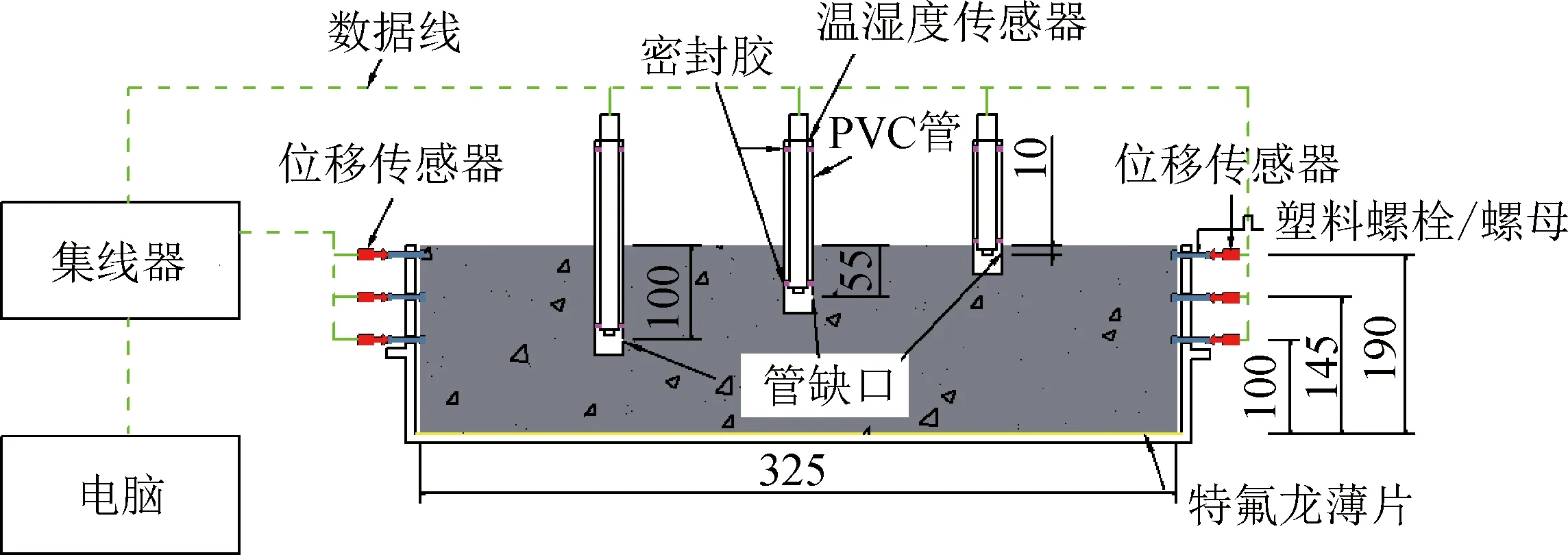
图2 混凝土收缩及湿度测试(单位：mm)Fig.2 Shrinkage and humidity test for the concrete (unit: mm)

为测得混凝土内部温度、湿度及应变在不同养护条件下的变化规律，设计了两种不同的混凝土养护方式：一为干燥养护，对于干燥养护的试件，在混凝土初凝拆模并安装完温湿度传感器和位移传感器之后开始试验，使得试件除地面以外均与外界发生湿度交换；二为密封养护。

研究中，试件编号的规则是：S和D分别代表试件处于密封状态和干燥状态，40和80分别代表混凝土的强度等级，0、45和90代表距离模具中心不同距离的测点。

1.3 混凝土基本性能测试

试验测量了C40和C80混凝土浇筑完成后72 h、168 h、336 h、504 h和672 h的立方体抗压强度、劈裂抗拉强度和弹性模量，测试结果见表2和表3。

表2 C40混凝土基本力学性能Table 2 Basic mechanical properties of C40 concrete

表3 C80混凝土基本力学性能Table 3 Basic mechanical properties of C80 concrete

2 结果与讨论

2.1 混凝土自由变形与温度的分布

图3展示了在干燥及密封养护条件下不同强度等级混凝土的变形与内部温度的发展情况。从图3中可以看出，混凝土内部温度变化可以划为三个阶段：(1)温度快速升高；(2)温度快速降低；(3)混凝土内外部环境达到热力学平衡状态，保持相对稳定的状态。

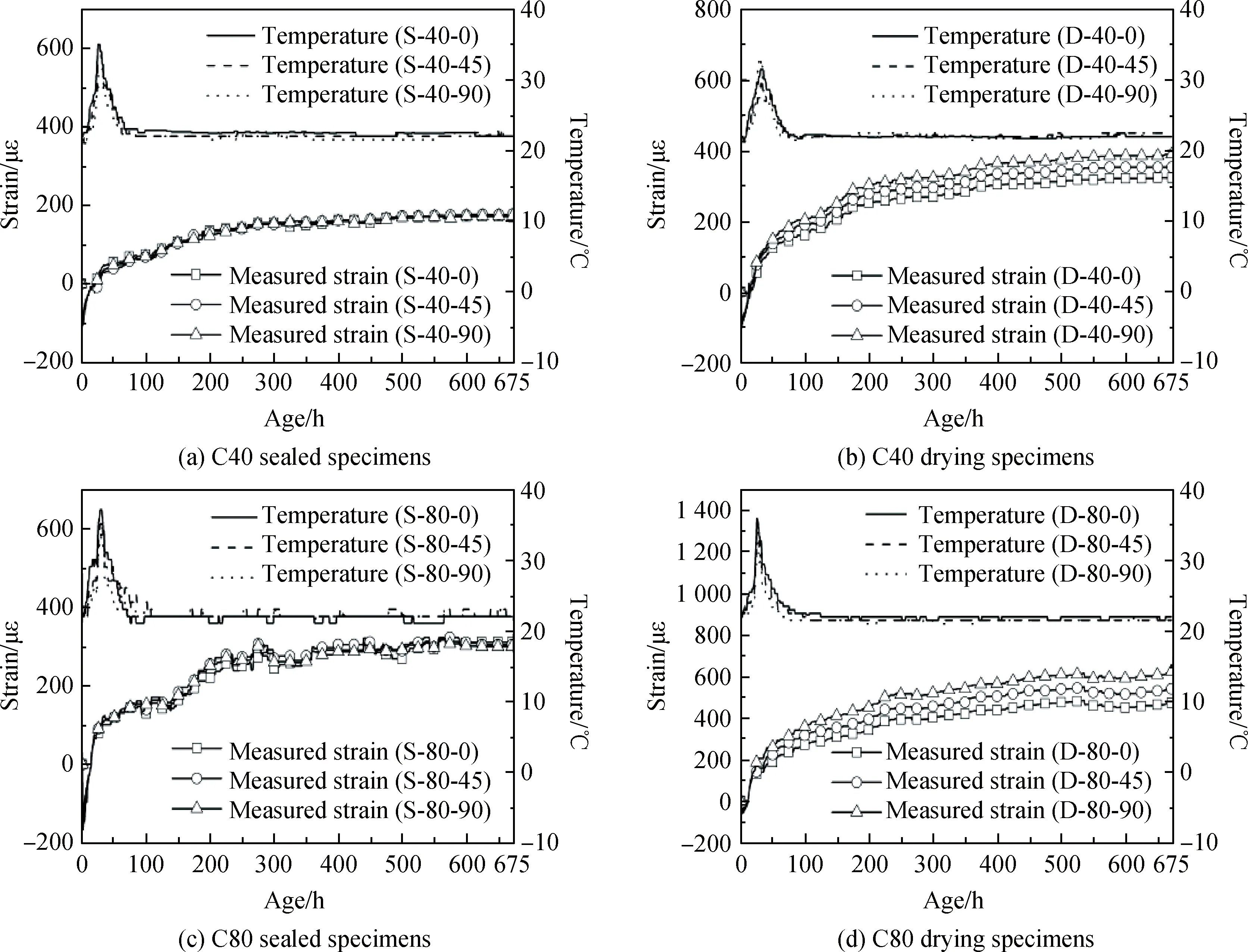
图3 密封和干燥养护条件下混凝土自由变形与内部温度Fig.3 Free deformation strain and temperature in concrete under the sealed and drying curing conditions

2.2 混凝土自由变形与湿度的分布及二者关系

为避免温度变形影响混凝土由湿度导致的变形分析的准确性，可以用公式(1)来计算仅由湿度变化导致的混凝土变形[8]：

εw=εm-εT

(1)

式中：εw是湿度导致的混凝土应变;εm是传感器测试到的应变;εT是温度导致的应变。

又由于：

εT=αΔT

(2)

式中：ΔT是混凝土温度变化，℃；α是混凝土热膨胀系数，με/℃。

因此，可用公式(3)来计算由湿度导致的混凝土变形：

εw=εm-αΔT

(3)

图4展示了在干燥及密封养护条件下不同强度等级混凝土的变形与内部湿度的发展情况。整体上来讲，混凝土内部湿度的变化可以划分为两个阶段：(1)湿度饱和阶段(相对湿度为100%)，混凝土的内部湿度在该阶段保持不变；(2)湿度下降阶段(相对湿度<100%)，随着水化反应的进行，水分由于消耗而减少，混凝土中的湿度持续降低[9]。

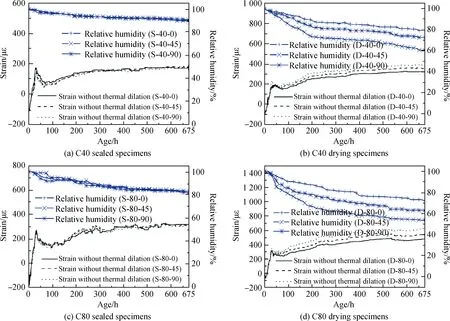
图4 密封和干燥养护条件下混凝土自由变形与内部湿度Fig.4 Free deformation strain and relative humidity in concrete under the sealed and drying curing conditions

与此同时，混凝土也在产生变形。在整个测试龄期内，可以将混凝土的收缩变形分为三个阶段：(1)由水泥水化热以及塑性沉降作用导致的膨胀阶段；(2)因毛细孔张力存在，混凝土停止膨胀并开始收缩的快速收缩阶段；(3)随着混凝土中水泥水化进程速度的下降，混凝土收缩速度逐渐下降，并使得混凝土收缩量逐渐保持相对稳定的值。

C40和C80混凝土收缩应变与内部湿度的关系见图5。从图5中可以得出，混凝土的收缩变形与内部湿度呈现出良好的线性关系。

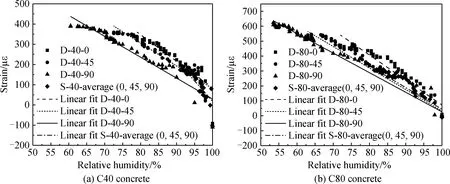
图5 混凝土收缩应变与内部湿度的关系Fig.5 Relationship between free shrinkage strain and relative humidity in concrete

由此可以推断，混凝土的收缩变形能够利用混凝土的内部湿度进行估算,则有公式(4)：

εw=εΙ+k(100-Hr)

(4)

式中：k是湿度每下降1%导致的应变，με/%；εΙ是在湿度阶段I时混凝土的收缩量；Hr是湿度。

C40和C80混凝土不同测点的参数取值见表4。

表4 公式(4)计算参数Table 4 Parameters of formula (4)

根据表4中参数的计算结果以及测试结果绘制图6。由图6可知，由湿度导致的混凝土应变可以用公式(4)得到很好的预测，然而在湿度饱和阶段(相对湿度为100%)混凝土的收缩与湿度间的关系并不显著。所以，公式(4)仅可用于估算湿度下降阶段混凝土的湿度。同时，与以往的研究成果进行对比可发现，水灰比、养护环境等因素也很可能对公式(4)中参数的取值产生影响[10]。

图6 公式(4)的计算结果与测试结果的对比Fig.6 Comparison of the formula (4) calculate results and test results

3 混凝土内部湿度场计算模型

本文建立了理论模型,通过和试验数据比对进而验证理论模型准确性，以便进一步获得混凝土内部湿度场、应力场的分布规律。

3.1 湿度扩散方程及其求解

有两个原因造成了混凝土内部水分的消耗，分别为水泥水化作用导致的毛细孔中水含量下降和干燥作用导致的毛细孔中水含量下降。考虑时间的因素，混凝土毛细孔中的相对湿度变化与水分含量变化的关系可用线性相关表达[11-12]，同时忽略温度改变产生的影响[13]，通过Fick第二定律[14]、傅里叶变换以及双曲正切函数近似计算法[15]得到混凝土内部湿度计算公式，即式(5)。所以，在已知混凝土湿度扩散系数、混凝土的初始内部湿度以及外界环境湿度的情况下，混凝土内部的湿度分布可利用式(5)计算：

(5)

式中：Hd为干燥作用导致的相对湿度降低值；He是混凝土所在环境湿度；H0是混凝土初始内部湿度；D是混凝土湿度扩散系数；x是混凝土内部到干燥面的距离；t是干燥时间。

3.2 混凝土湿度扩散系数

确定混凝土湿度扩散系数D值是求解式(5)的关键所在。在对以往的研究成果进行综合分析后，选用了Boltzmann变换对扩散系数进行反向求解。通过计算可以得出在试验条件下的混凝土湿度扩散系数：

(6)

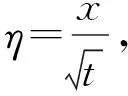
水泥水化作用和干燥作用共同导致了混凝土中湿度的下降，故在计算混凝土湿度扩散系数时，需要将混凝土水化导致的湿度下降量从总的湿度下降量中减去。图7为混凝土湿度扩散作用导致的湿度下降。

根据Akita等[16]的研究成果，湿度扩散系数可用数学模型式(7)来近似表达Hd与η关系以进行试验结果的计算：

(7)

式中：a、b、c、d为模型的系数，可以利用拟合试验结果得到。

由式(7)得到的拟合曲线与试验结果Hd和η的关系如图8所示，表5展示了模型采用的系数。

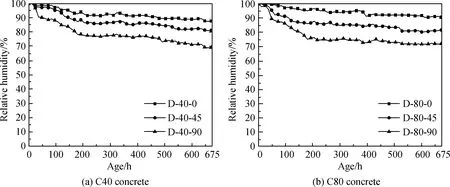
图7 湿度扩散引起混凝土内部湿度的变化Fig.7 Moisture change in concrete caused by humidity diffusion

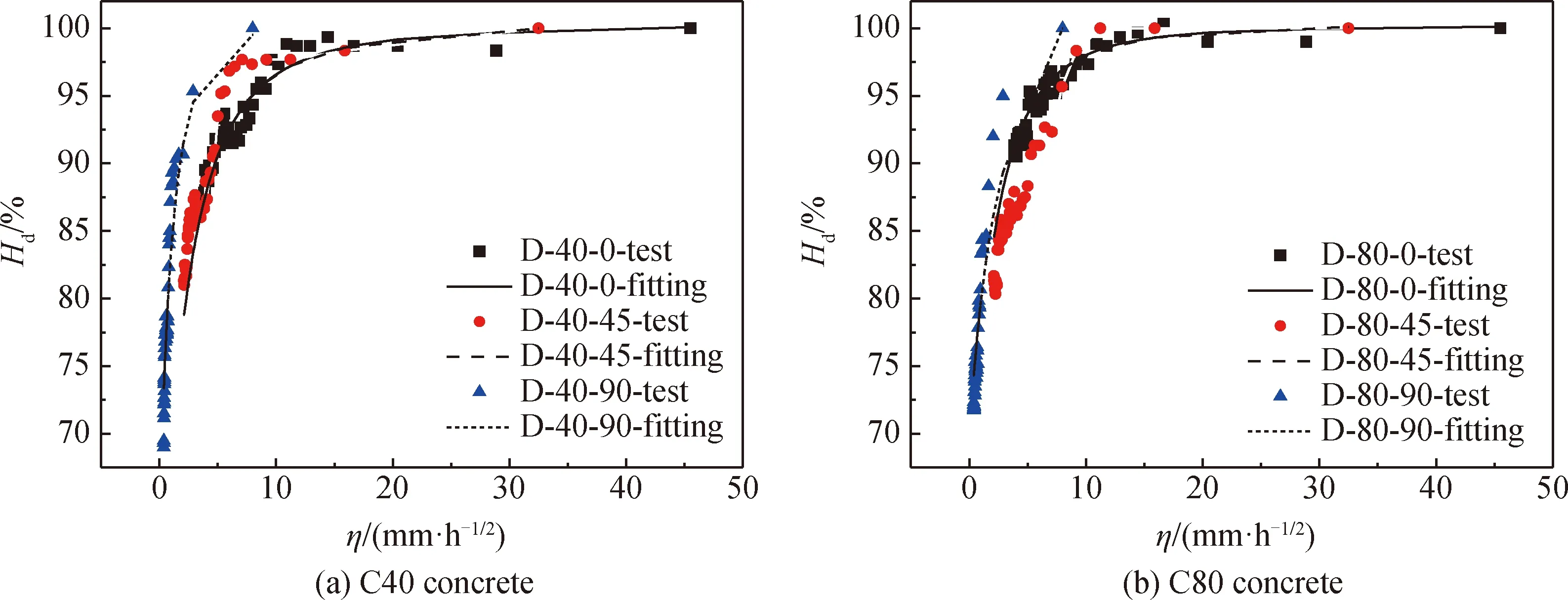
图8 干燥作用导致的混凝土湿度下降Hd和系数η的关系Fig.8 Relationship between Hd and η in concrete caused by drying

表5 计算模型参数Table 5 Model parameters of calculation

C40和C80混凝土湿度扩散系数随龄期的变化曲线如图9所示。由图9可知，混凝土的湿度扩散系数随龄期的变化规律可划分为三个阶段：(1)快速下降阶段，约在混凝土浇筑完成后0～80 h，混凝土的湿度扩散系数随龄期增加快速降低；(2)缓慢下降阶段，约在混凝土浇筑完成后的80～200 h，混凝土扩散系数随龄期增加下降速度减缓；(3)稳定阶段，约在混凝土龄期超过200 h以后，湿度扩散系数随龄期增加都不再显著变化。从图9中还可以看出，与干燥面的距离越大，混凝土湿度扩散系数越大。

图9 混凝土湿度扩散系数随龄期的变化规律Fig.9 Development of the moisture diffusion coefficient of concrete with age

C40和C80混凝土在相同湿度条件下各测点的湿度扩散系数如图10所示。由图10可知，在相同内部湿度条件下，同一种类的混凝土内部各点的湿度扩散系数十分相近。而且，混凝土的湿度扩散系数与混凝土内部相对湿度表现出良好的相关性。混凝土的湿度扩散系数随着湿度的降低而减小，大致可分为三个阶段：(1)当相对湿度超过95%时，湿度扩散系数迅速下降；(2)当相对湿度在80%～95%之间时，湿度扩散系数缓慢下降；(3)当相对湿度小于80%后，湿度扩散系数趋于稳定。主要原因为：当相对湿度超过95%时，混凝土内部的水分含量较高，混凝土内部的水以液态水为主，且主要以蒸发和流动的形式扩散；当相对湿度在80%～95%时,混凝土中的水分由主要为液态水向液态水和气态水共存的状态转变，在水分的扩散过程中,气态水的扩散的比例逐渐增加,从而导致水分扩散系数的降低；当相对湿度低于80%以后，水分以气态水为主，混凝土内部水的含量进一步下降。

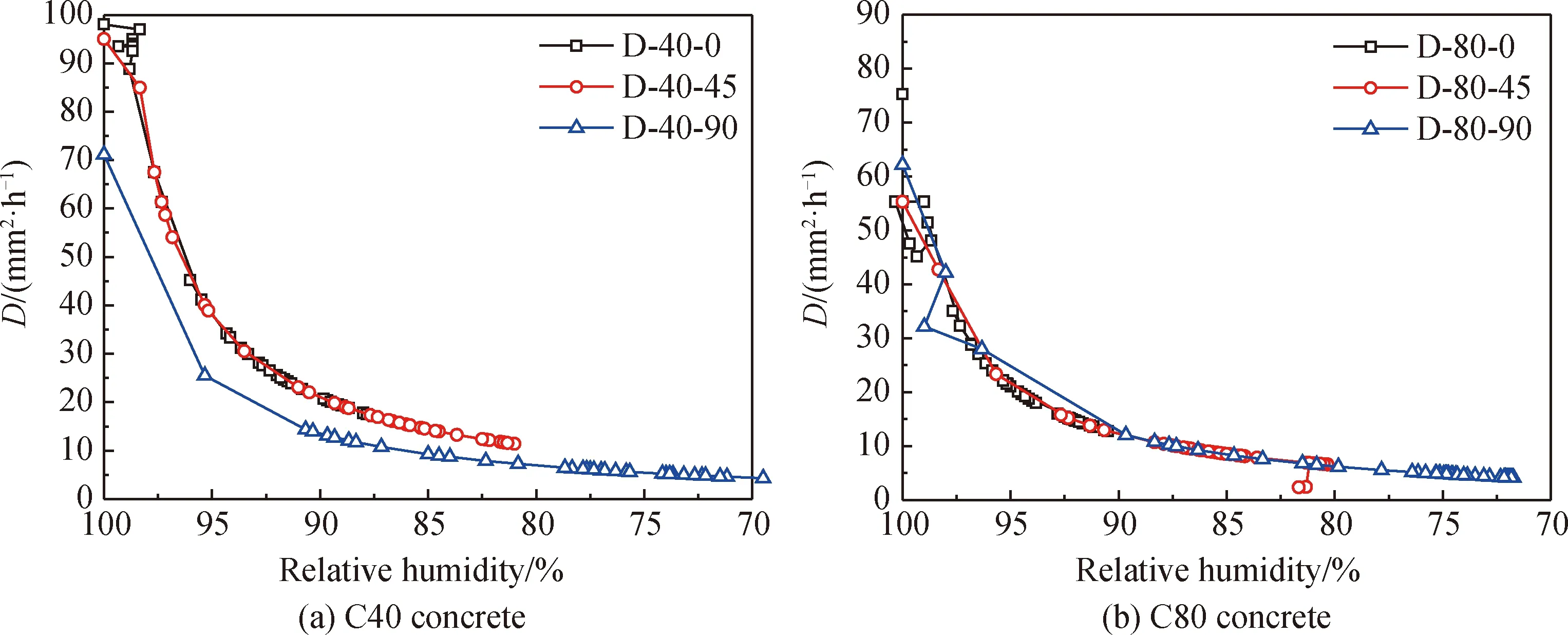
图10 干燥试件在相同内部湿度下的湿度扩散系数发展Fig.10 Development of the moisture diffusion coefficient of all the drying specimens with the same relative humidity

3.3 计算模型与试验结果的对比

利用公式(5)得到C40与C80混凝土内部湿度场分布的计算结果，其与测试结果的对比如图11所示。由图11可知，计算结果与测试结果基本吻合。对混凝土早龄期内部湿度认识不足导致的模型失真，以及误差函数的选取均可能对计算结果造成误差。但模型总体上仍能较好地预测混凝土内部湿度，同时误差造成的影响是放大了扩散作用导致的混凝土内部梯度，从而使得在计算混凝土自约束应力时偏于保守，故而这种误差类型应当是能够被接受的。

图11 混凝土内部湿度计算结果与实际值的对比Fig.11 Comparison of the calculate results and test results

4 混凝土内部应变与湿度的理论关系

为了建立混凝土内部应变与湿度的理论关系，将公式(5)代入公式(4)中可得任意时刻混凝土湿度扩散作用导致的混凝土内部应变分布的计算公式：

(8)

除此之外，还需考虑混凝土水化作用导致的湿度下降，才能计算实际条件下混凝土内部的应变分布。水化作用导致的湿度下降的计算可采用文献[17]提出的公式：

(9)

式中：Hs表示水化作用导致的湿度下降值；Hs,u表示水泥最终水化程度对应的相对湿度，它是与混凝土水灰比有关的函数，根据试验确定其具体的值；αc为水泥的临界水化程度，表示混凝土内部湿度从100%下降时的水化程度；α为在任意龄期时混凝土的水化程度；αu是混凝土的最终水化程度[18]；βu为参数，可由试验获得。

可由公式(10)求解混凝土的最终水化程度αu：

(10)

式中：w/c是混凝土的水灰比。

可参考式(11)计算[19-20]在任意龄期时混凝土的水化程度α：

(11)

式中：tk、q分别是计算参数，需通过混凝土的绝热温升试验获得；teq是混凝土的等效龄期，由公式(12)给出：

(12)

式中：t是混凝土的干燥时间；R为空气常数，可取8.314 J/(mol·K)；Uar和UaT分别表示参考温度Tr(通常取为20 ℃)和温度T(℃)时水泥的水化反应表观活化能，J/mol。依据文献[21]的研究成果可以得出：

UaT=(42 830-43T)exp(-0.001 7Tt)

(13)

依据文献[21]的绝热升温试验所获得的数据并根据公式(10)～(13)，可计算得到水泥水化作用导致的混凝土湿度下降值。本试验中C40及C80混凝土水化作用导致的湿度变化值的试验及理论计算结果的对比见图12，表6列出了相关参数。

因此，可由公式(14)表达应变与包含湿度扩散作用、水泥水化作用的混凝土内部湿度的关系：

(14)

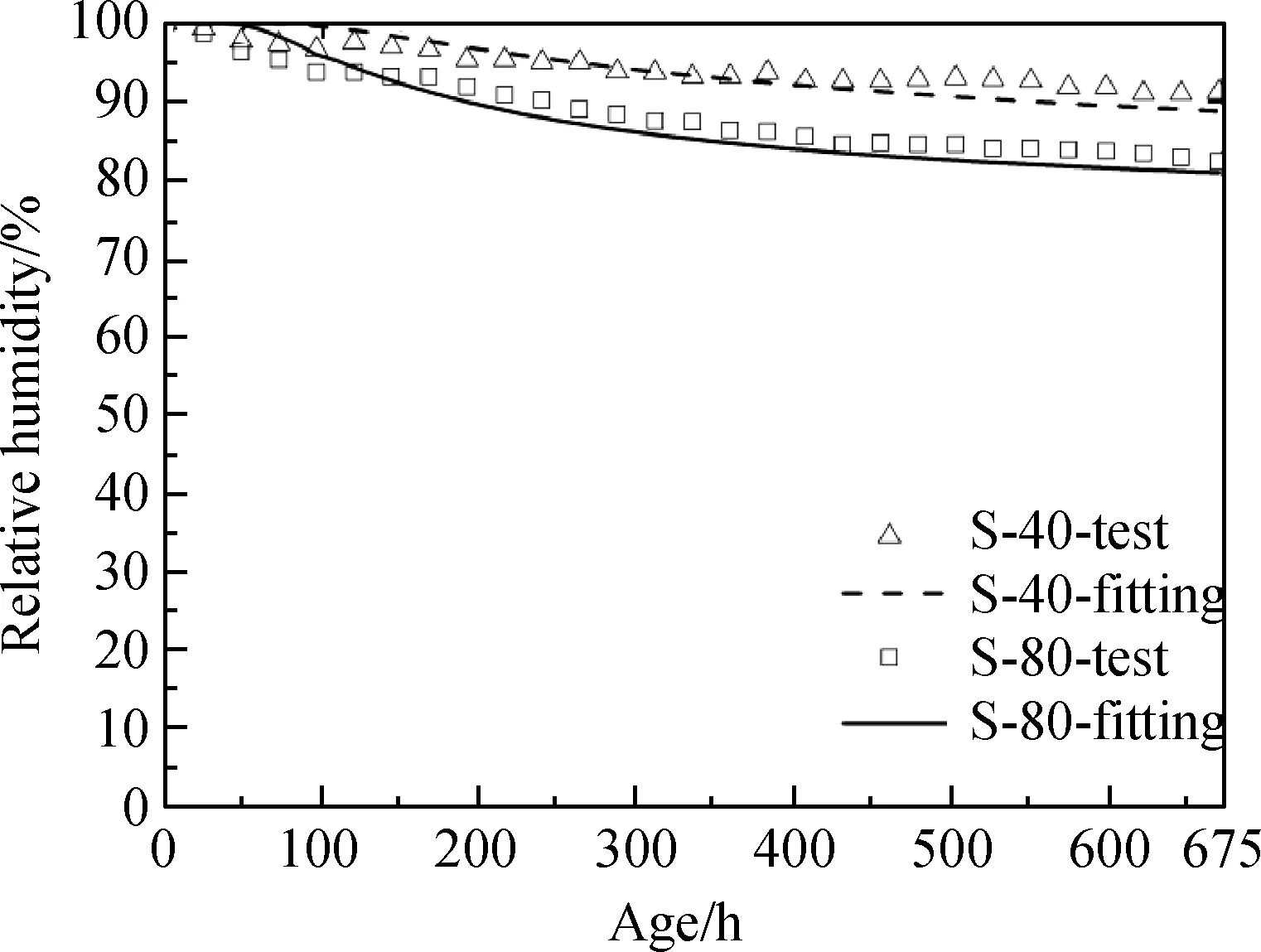
图12 水泥水化作用导致的湿度下降Fig.12 Decrease of relative humidity caused by cement hydration

表6 计算模型参数Table 6 Model parameters of calculation

5 混凝土自约束应力场的分析

上文试验及理论研究表明，在干燥环境作用下混凝土内部的水分扩散速度会因与干燥面距离的不同而不同，混凝土内部将会产生显著的湿度梯度，进而形成收缩变形梯度，从而在混凝土内部产生收缩应力。当这种收缩应力超过了混凝土的抗拉强度时，混凝土即会发生开裂。因此，有必要对收缩梯度导致的自约束应力场进行分析计算。

本文采用“等效荷载法”对混凝土收缩导致的内部自约束应力场的计算进行求解。

由非线性应变引起的内部自约束应力(σx)可用公式(15)表达：

(15)

式中：σ′x表示完全约束墙体施加的应力；σ″x表示释放轴力施加的均匀应力；σ‴x表示释放弯矩施加的拉压应力；x、y分别为混凝土长度和厚度方向；h为墙体厚度的一半；ε(y)为y方向的应变；Es表示混凝土相对于毛细孔应力的弹性模量。

此外，因为墙体的实际应力状态是平面应力问题，故最终的应力可用公式(16)表示：

(16)

式中：μ是混凝土的泊松比。

在同一龄期下，通过对试验得到的0 mm、45 mm、90 mm三个测点的收缩应变分析可以发现，不论混凝土强度等级的高低，混凝土沿高度方向的应变变化与二次函数呈现出较好的相关性。

因此，用公式(17)对混凝土沿干燥面方向上的应变分布进行假定：

(17)

式中：ε0表示在截面中心点处混凝土的应变；m表示与混凝土性能相关的参数。在本研究中，C40混凝土，m=0.25；C80混凝土，m=0.4。

图13展示了利用公式(17)计算得到的混凝土内部应变分布。由此可以发现，利用公式(17)能够对混凝土内部应变分布得出较好的预测效果。

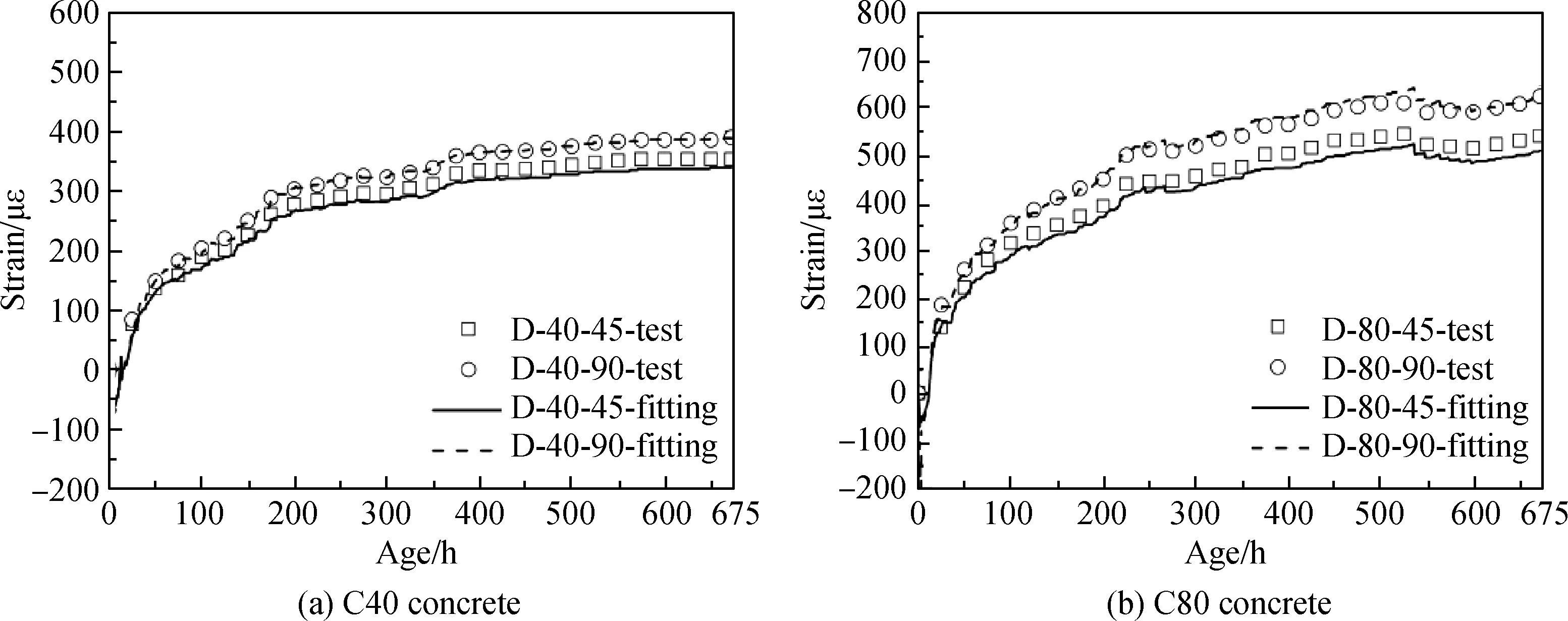
图13 公式(17)的拟合结果Fig.13 Fitting results of equation (17)

把式(17)代入式(16)中可得式(18)：

(18)

由于目前对于Es尚未有直接的测量方法。因此,在此使用混凝土的静力受压弹性模量替代Es来计算混凝土内部的应力。

通过公式(18)，对试验中的混凝土试件自约束应力场展开分析。C40混凝土和C80混凝土在0 mm、45 mm、90 mm测点的自约束应力随龄期的变化曲线如图14所示。可以发现，各个测点的自约束应力随着龄期的发展不断变化，并且在28 d时，C40混凝土0 mm、45 mm、90 mm测点的自约束应力分别为-1.4 MPa、-0.5 MPa和2.6 MPa。C80混凝土0 mm、45 mm、90 mm测点的自约束应力分别为-2.4 MPa、-0.9 MPa和4.9 MPa。通过对比试验结果可以发现，混凝土的抗拉强度大于由混凝土内部湿度场引起的自约束应力。所以混凝土在整个龄期内都不会开裂，这也与试验现象相符合。

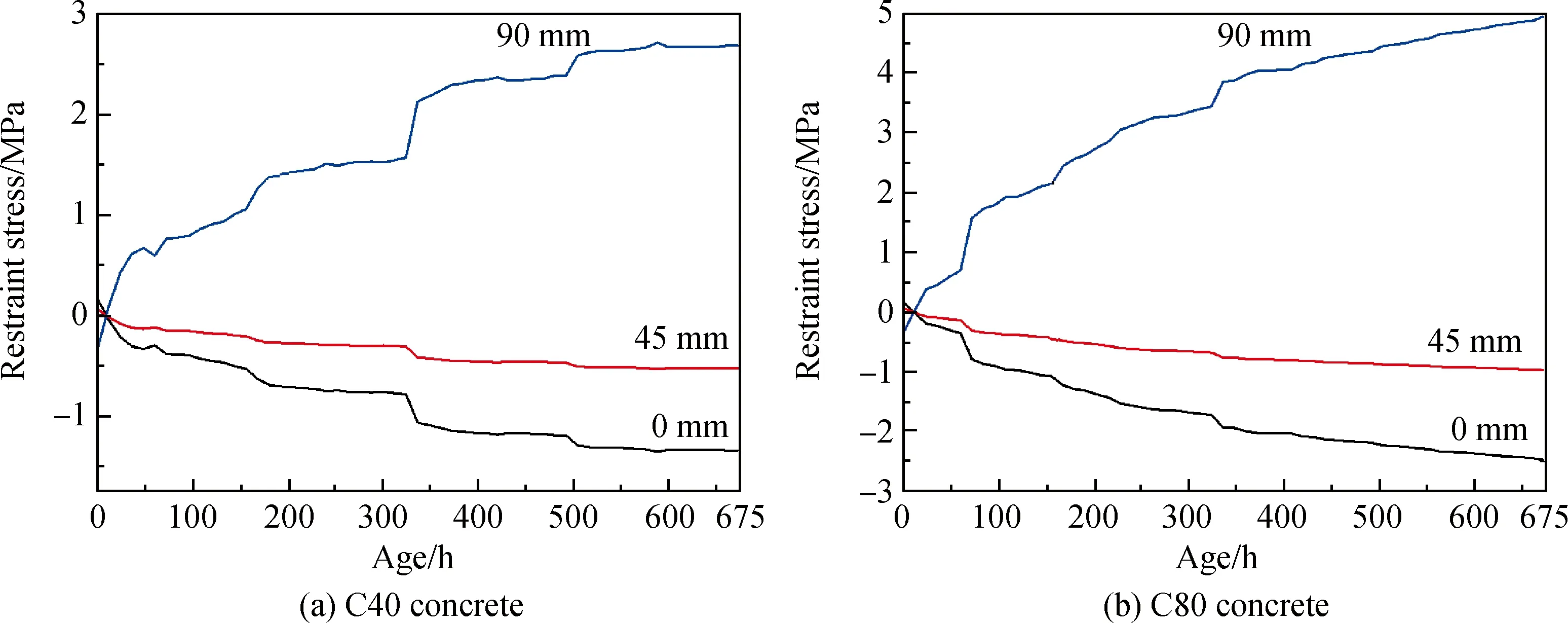
图14 试件内部自约束应力随龄期的发展Fig.14 Development of the self restraint stress in specimens

C40混凝土与C80混凝土内部自约束应力在不同龄期时沿高度的分布情况如图15所示。通过分析图15可以发现：随着混凝土龄期的增加，混凝土内部的自约束应力也随之增大；混凝土内部的自约束应力随着与干燥面距离的减小，逐渐由压应力向拉应力转变。C40混凝土和C80混凝土分别在试件高度约57 mm和58 mm附近出现内部0应力点，即压应力转变为拉应力。

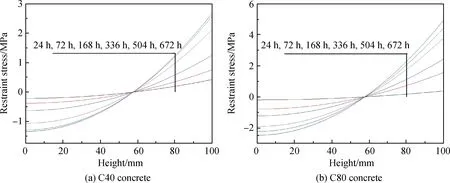
图15 试件内部自约束应力分布Fig.15 Distribution of the self restraint stress in specimens

6 结 论

通过试验及理论分析，本文对早龄期混凝土内部湿度、变形、自约束应力场及其相互关系进行了研究。根据研究成果可以得出以下结论：

(1)水泥的水化作用、干燥作用控制着混凝土的内部湿度。随着水泥水化作用增强以及干燥作用愈加显著，混凝土内部湿度下降的速度也越快。

(2)在整个测试龄期内，可以将混凝土的收缩变形分为三个阶段：由水泥水化热以及塑性沉降作用导致的膨胀阶段；因毛细孔张力的存在，使得混凝土停止膨胀并开始收缩的快速收缩阶段；随着混凝土中的水泥水化进程速度的下降，混凝土收缩速度逐渐下降，并使得混凝土收缩逐渐保持相对稳定的值。

(3)混凝土湿度扩散系数是表征其内部湿度的函数。由干燥作用导致的内部湿度扩散速度随着混凝土内部各点与干燥面的距离变化而不同，进而造成了在相同龄期下，随着与干燥面距离的增大，混凝土内部湿度扩散系数增大。

(4)混凝土的收缩变形与内部湿度之间存在显著的相关性，由内部湿度降低导致的普通强度混凝土、高强混凝土的收缩变形能够通过本研究给出的公式得到较好的计算结果。混凝土水灰比、养护环境等条件可能对公式中的参数造成影响。

(5)混凝土内部湿度场的存在导致了应变梯度的存在，使得混凝土内部产生自约束应力。但高强混凝土的收缩变形以及相对于毛细孔应力的弹性模量均高于普通强度混凝土，故其内部自约束应力高于普通强度混凝土。

综上可知，在混凝土结构施工过程中，应当充分重视由混凝土湿度梯度引起的内部自约束应力，可采用延长混凝土湿养护时间的方式，降低混凝土内部的收缩及收缩应变场。