天津软土地区盾构隧道地震响应分析及影响因素研究

李向辉，李永波，王志宇

（1.天津轨道交通集团有限公司，天津 300392；2.天津市政工程设计研究总院有限公司，天津 300392；3.同济大学 地下建筑与工程系，上海 200092；4.北京财贸职业学院，北京 101101）

强地震严重威胁着地下工程的结构安全，如1976年唐山大地震，天津地铁1号线在沉降缝处出现面层局部脱落和开裂的现象；1995年日本阪神地震[1～2]，造成大开地铁车站严重破坏；因此，随着大规模地铁工程的建设，学者对地下结构抗震安全性的重视提升到一个新高度。郜新军[3]建立三维区间隧道模型，研究了SV波斜入射下软硬土体相间场地中隧道结构的动力响应规律；梁建文等[4]研究了隧道间距对衬砌地震应力的影响；王国波等[5]建立了软土车站结构和相邻隧道的三维计算模型，分析了隧道对车站结构内力的影响。以上研究均取得了一些有益经验和结果。

本文以天津软土地区的地铁盾构隧道为研究对象，利用大型有限元软件ANSYS 19.0建立双隧道结构二维分析模型，研究土-盾构结构共同作用下的地震反应规律及结构抗震薄弱环节，为类似工程抗震分析及设计提供借鉴。

1 工程概况

天津地区为海积～冲积滨海平原地貌单元，地形总体较平坦。某地铁盾构区内场地土为中～软土，以新近淤积层淤泥、全新统新近冲积层粉质黏土层和其他淤泥质土为主；同时存在多条区域性断裂，如海河断裂、大寺断裂、天津北断裂等，这些断裂往往是地震易发场所。盾构管片覆土厚度一般在10～16 m。管片由C50混凝土预制而成，内径5.5 m、厚度350 mm。

2 数值分析模型

2.1 计算模型及参数

利用ANSYS 19.0软件建立软土-盾构双隧道结构有限元分析模型，两隧道中心间距取2.5倍管片计算直径，即14.6 m，计算直径为管片顶底中心间距离，见图1。

图1 软土-盾构隧道结构计算模型

根据实际工程盾构管片上覆土厚度，选取d为10、12、14、16 m共4种情况，以14 m覆土厚度为基本计算工况；为研究场地土剪切波速对管片动力响应的影响，场地土体的剪切波速Vs分别取100、120、150、200 m/s，以150 m/s为基本波速，同时考虑了剪切波入射角度对管片动响应的影响。左线盾构测点L1～L12按逆时针排序，右线盾构测点R1～R12按顺时针排列，相邻测点夹角为30°。

有限元模型计算区域长120 m、高60 m。土体为Plane42平面单元模型，密度取1 900 kg/m3，泊松比取0.36，弹性模型根据选取的剪切波速导出；盾构管片为钢筋混凝土结构，以BEAM3梁单元模拟，材料密度取2 500 kg/m3，弹性模量取3.45×104MPa，泊松比取0.2；人工边界以Combin14号弹簧模拟。

2.2 黏-弹性人工边界

分析地震动作用下场地土-结构相互作用响应规律时，需要在模型边界上设置适当的人工边界，以近似满足场地无穷远辐射条件要求。比较常用的人工边界有黏性边界、透射边界、黏-弹性边界等；其中，黏-弹性人工边界具有较好的频率稳定性和良好的适合性。杜修力等[6]对人工边界参数的取值作了合理修正，得到二维模型的弹簧刚度系数K及黏滞阻尼系数C。

式中：ρ、λ、G分别为介质密度、拉梅常数及剪切模量；CP、Cs分别为P波及S波在介质中的波速；r为散射波源到人工边界的距离；α、β为修正系数取α=0.8、β=1.1。

2.3 输入地震动

研究表明，地震动水平向分量是影响结构受力及造成结构破坏的主要因素，故在本次分析中，选取1976年天津宁河波和1940年美国El Centro波水平向地震动加速度记录并根据外源输入理论转化为位移时程和速度时程作为场地模型的输入地震动。两条地震动的卓越频率分别为1.12、1.46 Hz，就整体所含频谱成分而言，天津宁河波以低频成分为主。见图2。

图2 场地输入地震动加速度时程曲线

根据天津地区轨道交通地震安全性评价报告，场地地震设防烈度为Ⅷ度，Ⅲ类场地。模型计算分析时，将两条输入地震动的加速度峰值均调整为2.0 m/s2。

3 结果分析

3.1 入射角度的影响

覆土厚度14 m、场地土剪切波速150 m/s时宁河波作用下，左线盾构管片不同位置处弯矩差别明显且随地震动入射角度增大，不同位置处的弯矩峰值变化显著。其中，L1、L4、L7、L10号测点在地震动垂直入射时的弯矩最小，最大值仅为16.1 kN·m；随入射角度增大上述4测点处弯矩几乎以相同的幅度增大，10°、20°角入射时增大至最大，分别为110.0、211.3 kN·m；而其他各测点则随地震动入射角度增大不同幅度减小。同样地，右线盾构管片不同位置处弯矩值的变化趋势与左线盾构相同。见图3。

图3 左线盾构隧道不同观测点弯矩峰值

因左右线盾构管片测点编号以模型中心轴对称布置，在地震动垂直入射下，左右线相同测点的弯矩值相等，最大弯矩220.0 kN·m。在宁河波斜入射下，右线R3、R6、R9、R12测点较左线对称测点处弯矩增大，10°角作用下增大幅度最大，为12.05%，弯矩最大值为211.3 kN·m；20°角作用下增大幅度最大，为12.95%，弯矩最大值为211.2 kN·m。右线其余各测点弯矩在地震动斜入射下均较左线减小。弯矩峰值普遍出现在地震动垂直入射时。见表1。

表1 地震动作用下左右线管片各测点弯矩kN·m

3.2 地震频谱的影响

地震动的频谱特性对结构弯矩影响显著，对软土地区来说，低频成分的地震动对盾构管片弯矩的影响较大。覆土厚度14 m、场地土剪切波速150 m/s时，El Centro波以不同入射角度作用下，左线盾构隧道不同测点处弯矩值的变化趋势大致与宁河波作用下相同，但相同入射角度作用下同一测点的弯矩值差别显著。以L3号测点为例，El Centro波垂直入射和10°角入射时的弯矩峰值分别为105.1、91.2 kN·m，而宁河波以同样的角度入射时，弯矩峰值分别为196.5、171.0 kN·m，较El Centro波弯矩峰值分别高出约87.0%、87.5%。见图4。

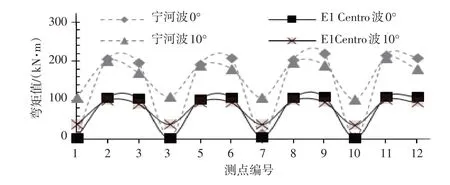
图4 不同频谱地震动下左线盾构隧道测点弯矩峰值

3.3 覆土厚度的影响

埋深较大的盾构隧道地震动响应较显著。场地土剪切波速150 m/s时，宁河波垂直入射下不同覆土厚度，除1、4、7、10号测点弯矩峰值很小且几乎相等外，其余测点处的弯矩峰值随覆土厚度增大逐渐增大，但增大的幅度逐渐减小。以3号测点为例，覆土厚12 m的弯矩峰值较10 m增大了12.8%；覆土厚14 m的峰值较12 m增大了10.8%，覆土厚16 m的峰值较14m增大了9.9%。见图5。

图5 不同覆土厚度的盾构隧道测点弯矩峰值

3.4 场地土剪切波速的影响

场地土质越软，低频成分为主的地震动对盾构结构造成的破损越严重。宁河波垂直入射、不同剪切波速场地下，1、4、7、10号测点弯矩峰值很小且几乎相等，其余各测点处的弯矩峰值随剪切波速的增大逐渐减小，但减小的幅度逐渐增大。以3号测点为例，Vs为120 m/s时的弯矩峰值较100 m/s时减小了19 kN·m，即剪切波速每增大10 m/s弯矩峰值减小3.7%；Vs为150 m/s时的弯矩峰值较120 m/s时减小了43.4 kN·m，即剪切波速每增大10 m/s弯矩峰值减小6.0%；Vs为200 m/s时的弯矩峰值较150 m/s时减小了64.6 kN·m，即剪切波速每增大10 m/s弯矩峰值减小6.6%。见图6。

图6 不同剪切波速场地下的盾构隧道测点弯矩峰值

4 结论

1）与垂直入射相比，地震动斜入射时盾构管片不同位置处的弯矩峰值差逐渐减小，其中水平向和竖向4个测点的弯矩峰值显著增大，其他测点的弯矩峰值递减；但弯矩峰大值普遍出现在地震动垂直入射时。

2）因左右线盾构隧道关于模型的对称性，在地震动垂直入射下，左右线相同测点处的弯矩值相等；但在地震动斜入射下，右线隧道弯矩峰值在不同测点处较左线隧道增大或减小。

3）地震动的频谱特性对结构弯矩影响显著，对软土地区来说，低频成分的地震动对盾构管片弯矩的影响较大。

4）地震动作用下，隧道弯矩峰值随埋深增大，呈逐渐增大趋势。

5）对天津中软土场地来说，土质越软，低频成分为主的地震动对盾构管片结构造成的损伤越严重。