基于排队论对游乐场排队问题的研究及系统的初步设计

李 卓 崔 瑶 郑 超 郭 峰 钟智强

（重庆交通大学信息科学与工程学院，重庆 400074）

0 研究背景

2019 年末，全国共有A 级景区11 924 个，全年接待总人数60.24 亿人次，比2018 年末增长了10.5%[1]。随着时代的发展，游乐场与景区的发展会越来越好，游客的数量也会越来越多。游乐园与景区在接待如此多的游客的同时，经常会出现“排队两小时，游玩三分钟”的现象，这些现象在一定程度上降低了游客的游玩体验，导致游乐场及景区的口碑下滑。另外，还经常会出现游客抱怨游乐场和景区路标指引不清晰的问题。因此，需要通过解决上述问题来提升游客的游玩体验和游乐场的收益。

笔者通过查阅相关资料发现，目前游乐场排队系统大多只是展示不同项目的排队人数与预计排队时间，功能单一，不能解决实际存在的排队问题；排队人数是由预约人数或者刷卡人数来决定的，这就会在一定程度上导致数据不准确，并且当前游乐场及景区排队系统也没有路线规划等较为复杂的功能。该文旨在解决游客的排队问题、路线规划问题，为游客创造更好的游玩体验，也为游乐场及景区的管理人员提供更多的帮助，分担他们的压力。

1 排队模型的建立与求解分析

针对游乐场排队问题，笔者通过查阅文献[2]，构建出游乐场排队的数学模型，类似M/M/1 排队模型。该模型是一种出生-死亡过程，在该随机过程中的每个状态代表模型中人数的数量。但是排队是有上限的，即当队伍的长度达到一定程度时就不再增加，例如状态0 表示模型闲置，状态1表示模型有一人在接受服务。在该模型中，出生率（即加入队列的速率）λ在各状态中均相同，死亡率（即完成服务离开队列的速率）μ在各状态中也相同（除了状态0，因其不可能有人离开队列）。因此，在任何状态下，只可能发生2 种事情：1）有人加入队列。如果模型在状态k，它会以速率λ进入状态k+1。2）有人离开队列。如果模型在状态k（k≠0），它会以速率μ进入状态k-1。

针对这样的模型背景，对M/M/1 模型进行适当修改，建立符合当前问题的模型。

1.1 模型假设

假设队伍长度最大为N人，游客看到长度为N时直接离去。

假设同一个项目排队列数只有1 列。

1.2 模型建立

因为游客到达时间的间隔是随机的，所以假定其服从参数呈负指数分布[3]。

服务时间对于一些有固定服务时间的游玩项目（例如过山车、海盗船等），就可以固定其游玩时间。假设可以根据统计求出其平均时间，而对于鬼屋等一些参观游览型项目，假设其服从参数呈负指数分布。

关于参数的确定，笔者通过查阅相关资料并进行了初步统计，最终确定的具体做法如下：统计每个项目每天每个时间段到达的人数，然后根据动态数据分析得出其参数，将参数作为每个项目的参数。当然后期随着数据的积累也可以利用神经网络等预测方法去预测第二天的数据。

1.3 模型求解

笔者利用MATLAB，通过蒙特卡洛模拟法模拟出1 d 的排队情况，取游乐场1 d 的开放时长为8 h（480 min），模拟出30 d 的数据并取平均值。

具体算法为先根据统计等方法得出游乐场各个项目到达人数与服务时间所服从的分布参数，以以下4 个项目为例，参数是通过查阅相关资料得来的。

根据所服从分布随机生成每个人的到达时间与离开时间，计算游客的信息。当排队人数大于最大排队人数时，游客直接离去；当超过1 d 的工作时间时，算法终止。计算得到等待时间、总人数以及各个时间的队长等数据，进而可以求出平均等待时长，累计30 次的结果求取平均值。相关算法流程如图1 所示（以鬼屋为例）。

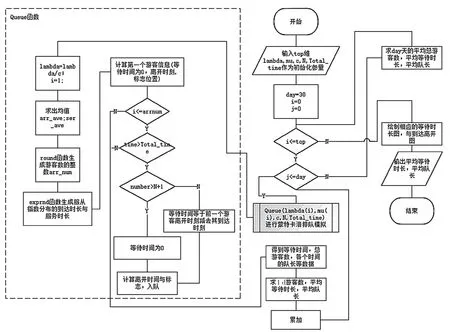
图1 鬼屋项目模拟流程图

最后模拟结果如图2 所示，横坐标表示第i个游客，纵坐标为游客的等待时间。对图2 中的结果进行分析，笔者得出了项目的排队时长及每个时间段到达的人数分布不均衡的结论。可以看到，过山车的最高等待时长接近2 h，平均等待时长达到30 min；而相比较之下，鬼屋的最高等待时长为16 min，平均等待时长只有2 min。排除项目本身吸引人的程度这些难以控制的因素之外，还有项目的分布也会造成游客选择的集中。游客可能会在同一时间尝试相同的项目。过山车等较靠近入口的项目总是排满了长队，而在鬼屋或者其他较为偏僻、不容易被发现的项目却十分冷清。因此，考虑设计排队系统来解决排队问题。

图2 项目游客的等待时间

表1 项目参数选取

2 排队系统的整体设计

笔者准备开发一个游乐场排队系统，初期先设计出Web界面，推出相应功能之后，将其移植到微信小程序或手机App，应用于旅游景点或游乐场，当游客使用App 或小程序时，为游客提供智能排队服务。

该项目的目标是缓解游乐场超长排队的现象、改善游客体验、为游客提供更好的游玩路线、提升游乐场的利益以及帮助管理者进行数据查看与统计分析。因此，该项目为管理者提供数据大屏显示、数据统计维护等多个功能；为游客提供路线规划、项目排队人数查询以及等待时间查询等功能。

2.1 面向游客——项目查询功能

进入系统后，可以看到项目的实时排队人数以及项目的预计排队时长。该功能可以帮助用户就近选择喜欢的项目，根据自己的判断做出取舍。项目展示的信息有当前该项目排队人数、预计排队时间、从当前地点前往目的项目的路程以及路程所需要的时间。这些信息可以帮助游客判断并挑选自己最想去的项目。

2.2 面向游客——电子地图功能

电子地图展示当前定位，游客输入目标地址后开始导航。

电子地图可以很方便地帮助游客了解整个游乐场的组成。游客可以清楚地知道自己处于游乐场的哪个位置，而且通过搜索功能可以快速地查找游乐项目，并通过导航到达目的位置；也可以单击地图中的各项目，查看该项目当前的排队信息等。

2.3 面向游客——路线规划功能

路线规划的具体操作流程如下：1）路线优先。①选择任意一种规划方式后再选择想优先玩耍的项目，如果没有则跳过；如果用户选择的优先玩耍的项目当前排队人数超过一定值，就提醒用户适当改变选择。②选择完成后，根据选择对路线和项目进行顺序规划。③网页展示规划路线以及项目顺序。2）综合最优。①根据综合评价法给出的最佳推荐项目。②系统展示推荐项目和项目信息。

2.4 面向管理者——数据统计功能

系统会把实时统计的人数按一定的时间间隔发送给后台数据库，可以使管理员统计当前游乐园的各种信息。

2.5 面向管理者——管理维护功能

管理维护功能是对用户线上购票信息进行管理，可以使管理者对用户账号进行操作，为其增加项目等。

2.6 面向管理者——数据分析优化建议功能

根据统计的信息，对未来游乐园的游玩人数进行预测，可以帮助管理员对数据进行分析，并且对前面的模型理论进行策略上的调整。

3 结论

基于排队论对游乐场排队问题的研究，使研究人员更加清晰地认识到了游乐场排队问题亟待解决，因此研究人员提出设计游乐场排队系统。设计的基本架构从问题点游乐场排队分布不均衡入手，设计了解决问题的相关功能。能够有效地提高游乐场的排队效率，且可以方便游客选择合适的下一站以及为游客规划合适的路线。系统区别于传统的功能单一的排队系统，该系统利用排队论来分析问题，对深入研究问题有深刻的意义，采用该方式进行分析，可以帮助管理者去发现问题，并针对存在问题进行合理规划与调整。