冷弯薄壁型钢拼合箱形柱的畸变屈曲性能研究

李艳春，周天华，丁嘉豪，李晨阳，张兴春

摘   要：为研究冷弯薄壁型钢（CFS）拼合箱形截面柱的畸变屈曲性能，首先对9根C形截面柱、9根U形截面柱及21根由C形和U形拼合而成的箱形截面柱进行轴压试验研究和数值模拟分析，考察其屈曲模式特征和受力特性. 在此基础上，提出一组假设模型以研究螺钉间距对拼合箱形截面柱变形特征和极限承载力的影响规律及其与试件半波长之间的关系. 研究结果表明：1）不同螺钉间距的试件，畸变屈曲半波数量和半波长（λc）均不相同. 2）螺钉间距小于0.9λc时，箱形截面柱的承载力大于C形和U形柱的承载力之和，即1+1>2的拼合效应. 3）螺钉间距大于0.9λc时，箱形截面柱的承载力逐渐接近C形和U形柱的承载力之和，即1+1≈2. 为计算CFS拼合箱形截面柱的极限承载力，在美国规范中直接强度法的基础上提出了一种计算箱形截面柱畸变屈曲弹性临界荷载的方法，将计算的临界屈曲荷载用于直接强度法以得到拼合箱形截面柱的极限承载力，理论计算结果与试验及有限元结果均比较吻合，验证了本文提出方法的准确度和适用性.

关键词：冷弯薄壁型钢;拼合箱形柱;畸变屈曲;屈曲臨界荷载;计算方法

中图分类号：TU391;TU317.1                     文献标志码：A

Investigation on Distortion Buckling Behavior of Cold-formed

Thin-walled Steel Built-up Box-section Columns

LI Yanchun，ZHOU Tianhua，DING Jiahao，LI Chenyang，ZHANG Xingchun

（School of Civil Engineering，Changan University，Xian 710061，China）

Abstract：In order to study the distortional buckling behavior of cold-formed steel（CFS） built-up box-section columns，firstly，9 C-section columns，9 U-section columns，and 21 built-up box-section columns composed of C-section and U-section were investigated by the axial compression tests and numerical simulation. The buckling characteristics and mechanical behaviors of the columns were investigated. On this basis，a set of hypothesis models were proposed to study the influence of screw spacing on the deformation，the ultimate capacity，and the relationship between the screw spacing and the half-wavelength（λc） of CFS built-up box-section columns. The results show that：1） The number and half-wavelength of distortion buckling are different for the specimens with different screw spacing. 2） When the screw spacing is less than 0.9λc，the ultimate capacities of built-up box-section columns are greater than the sum of the ultimate capacities of C-section and U-section columns，that is，the splicing effect of 1+1>2. 3） When the screw spacing is greater than 0.9λc，the ultimate capacity of the built-up box-section column is  gradually close to the sum of the ultimate capacities of the C-section and U-section columns，i.e. 1+1≈2. In order to calculate the ultimate capacities of CFS built-up box-section columns，an approach to predict the elastic critical load of distortion buckling was proposed based on the direct strength method（DSM） in American code，and then the calculated results were applied to the DSM to obtain the ultimate capacity of CFS built-up box-section columns. The results obtained from the calculation method are in good agreement with the experimental and numerical simulation results，which suggests the accuracy and applicability of the proposed method in this paper.

Key words：cold-formed thin-wall steel;built-up box-section columns;distortional buckling;critical buckling load;calculation method

在实际工程中，冷弯薄壁型钢（CFS）构件的结构形式和受力情况日益复杂，使得单肢构件往往难以满足设计和工程使用要求，因此拼合构件在实际工程中被应用. 其中，由1根C形和1根U形截面CFS构件经自攻螺钉拼合而成的CFS箱形构件在CFS结构住宅体系中运用越来越广泛. 因此，对CFS箱形截面拼合构件受力性能进行研究具有深远的意义.

相对局部屈曲和整体失稳，畸变屈曲是一类具有特殊性的稳定问题，因为截面失稳时既包含一部分板件发生弯曲的局部屈曲特征，又包含另一部分板件绕强迫转动轴（即板件交线）的扭转屈曲变形特征. Lau和Hancock[1]最初对卷边槽形截面构件进行受压试验研究，认为畸变屈曲没有屈曲后强度. Kwon和Hancock[2]对高强钢材卷边槽钢试验研究发现试件畸变屈曲后仍具有一定的强度储备，但是远小于局部屈曲后强度，并给出了工程中钢构件设计时避免出现畸变屈曲变形的建议. 管宇等[3]研究的轻钢组合楼盖中就用到该拼合构件以提高整体楼盖边缘刚度. 因此它的受力特性及变形特征也备受关注. Young等[4]和Zhang等[5]对由∑形截面组成的拼合箱形柱进行试验研究，并采用直接强度法[6]计算了试件的局部屈曲、畸变屈曲和整体屈曲三种屈曲模式下的极限承载力，但拼合闭口截面发生的畸变屈曲相对复杂，作者没有进行详细的描述;李元齐[7]等人对Q550高强CFS拼合箱形截面进行轴压试验，提出了一种计算该拼合截面构件承载力的简化设计方法[8]，但均未对拼合箱形截面柱畸变屈曲相关特性及其影响因素进行详细研究. 拼合箱形截面构件的畸变屈曲特征是C形截面组成构件卷边带动翼缘内扣而不发生外张现象，因为外包U形截面组成构件对C形截面组成构件外张有一定的约束作用，这在一定程度上减弱了畸变屈曲变形幅度，从而增强了整体构件屈曲后强度. 因此，对实际工程中常用的CFS拼合箱形截面构件的受力特性及变形特征的研究具有一定的实际意义.

由上述及查阅相关文献[9-14]发现，学者对CFS箱形截面拼合构件畸变屈曲特性的研究甚少，并且对于该拼合截面的临界屈曲荷载及极限承载力，目前仍没有准确的计算方法. 鉴于此，本文对9根C形柱、9根U形柱和21根由C形、U形拼合而成的箱形截面柱进行轴压试验研究，详细研究其畸变屈曲变形特征及受力特性. 首先，本文设计四种截面尺寸、四种螺钉间距以研究截面几何尺寸、螺钉间距分别对CFS拼合箱形轴压柱畸变屈曲变形特征、屈曲临界荷载和极限承载力的影响规律. 其次，为进一步研究该拼合截面柱畸变屈曲特性，进行了一系列数值模拟分析，然后根据试验和有限元分析CFS拼合箱形柱畸变屈曲的变形特征及受力性能，为实际工程设计提供参考. 最后，提出拼合箱形截面柱屈曲临界荷载[15]的计算方法，并将计算结果用于直接强度法[6]以得到拼合箱形柱的畸变屈曲极限承载力，解决了目前无准确计算拼合截面试件屈曲临界荷载公式的问题.

1   试验概况

1.1   试件设计

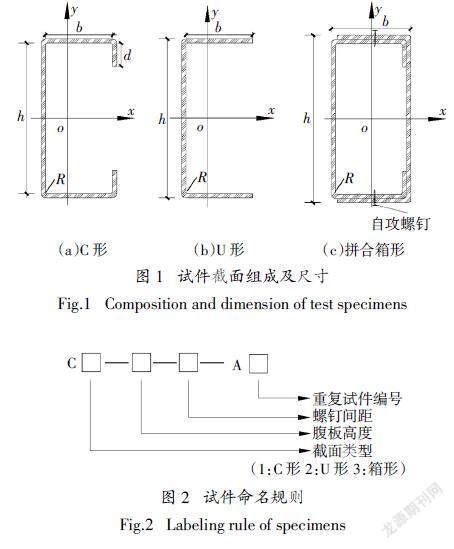
CFS拼合箱形截面柱由C形和U形截面通过自攻螺钉ST4.8连接拼合而成，设计三种截面形式如图1所示. 按C形截面腹板高度分为140 mm、160 mm、180 mm三个系列，试件编号规则见图2. C形截面尺寸分别为：140系列140 mm×40 mm×15 mm×1.5 mm;160系列160 mm×130 mm×12 mm×2.5 mm;180系列180 mm×140 mm×12 mm×2.5 mm，外包U形截面几何尺寸均以C形截面尺寸匹配. 140系列、160系列和180系列试件的长度分别为450 mm、1 500 mm和1 500 mm. 另外，试件的局部和整体初始缺陷的测量工具如图3所示，其中拼合构件的初始缺陷是由单根构件拼合后测量的.

螺钉间距以试件半波长为依据而设计且沿翼缘中间纵向排列. 立柱上下端部各设置280  mm × 360 mm × 16 mm端板，通过角焊缝与冷弯薄壁型钢拼合截面立柱相连接，如图4所示.

1.2   试件材性

冷弯薄壁型钢各构件依据《金属材料拉伸试验》（GB/T228.1—2010）[16]中的规定确定钢材主要性能指标，如表1所示.

1.3   试验装置

采用电液伺服程控结构试验机系统和反力门架施加竖向荷载，通过DH3816静态应变测试系统采集应变和位移数据. 试件的边界条件为两端固结，试验装置示意图及实物图，如图4所示.

1.4   测点布置

在柱中和上下1/4截面处布置应变片和位移计，截面内外均粘贴应变片，以便测出试件的屈曲临界荷载. 此外，在上端板架设一支位移计（D1）测量竖向位移，应变片、位移计布置如图5所示

2   试验过程及现象

2.1   试验现象及破坏特征

1）140系列试件，加载初期，试件的腹板和翼缘沿长度方向上均出现波浪状鼓曲波，随后C形截面试件翼缘-卷边棱线弯曲变形，即畸变屈曲，见图6. 拼合箱形试件中C形截面翼缘及卷边的变形被U形截面遮盖，故试验过程中不易判断拼合箱形截面是否发生畸变屈曲，但试验后把箱形截面的U形拆去，可观察C形截面出现畸变屈曲，见图6（c）.

2）160系列试件，141 kN左右时C1-160-0-A1中部左右翼缘外张，而C1-160-0-A2和C1-160-0-A3试件左右翼缘内扣;距上端300 mm處左右翼缘内扣，而C1-160-0-A2和C1-160-0-A3试件左右翼缘外张，如图7（a）所示. 61 kN左右时，C2-160-0-A1～A3试件中部距上端板310 mm处左右翼缘外张，随着荷载增加，自上而下均出现3个半波，如图7（b）所示. 随着荷载增加，C3-160-300-A1～A3试件中U形构件翼缘自上而下均出现3个半波且现象明显，如图7（c），而试件破坏后的剖面图中可以观察到C形构件发生畸变屈曲，如图7（d）所示. 100 kN左右时，C3-160-600-A1 ～A2试件中U形构件翼缘分别在距上端450 mm和500 mm处外张，而C3-160-600-A3在距下端380 mm处外张，随着荷载增加，3个试件U翼缘均在螺钉间距之间出现外张，如图7（c）所示. 70 kN左右时，C3-160-1000-A1～A2试件中U形构件翼缘分别在距上端200 mm处外张，而C3-160-1000-A3在距下端50 mm处外张，随着荷载增加，3个试件U翼缘均在螺钉间距之间出现外张，达到峰值后，C和U形构件的腹板中部均有外凸现象，而试件破坏后的剖面图中可以观察到C形构件发生畸变屈曲如图7（d）所示. 每组3个试件之间出现破坏位置不同的原因主要是初始缺陷造成的.

3）对于180系列试件，单肢C形柱和拼合箱形柱均发生畸变屈曲，具体的试验现象与160系列试件类似，仅屈曲临界荷载及破坏位置不尽相同，具体试验现象见图8.

2.2   试验承载力

各试件的承载力试验值及试件初始缺陷如表2和表3所示. 其中Pt1、Pt2和Pt3分别为C形截面、U形截面和箱形截面试件的承载力试验值;Py1和Py2分别为C形截面和U形截面的屈曲荷载. 由表2和表3可知：

1）无论是单肢试件还是拼合截面试件Pt  /Py总小于1，说明试件破坏时不能达到强度破坏的极限状态，主要是因为失稳变形的二阶效应对承载力的削弱作用. 140系列单肢C形截面柱发生局部-畸变屈曲模式，说明该屈曲模式对单肢截面柱的承载力更加不利. 单肢U形截面柱均发生局部屈曲且随着腹板高度增加，极限承载力增大.

2）140系列拼合柱仍发生LD模式屈曲，而160系列和180系列发生D屈曲，众所周知，畸变屈曲仅发生于C形截面，U形截面发生局部屈曲，而拼合截面的畸变屈曲可由其剖面观察出，如图7和8所示.

3）由表3可知，拼合箱形柱极限承载力总大于两单肢极限承载力之和，说明拼合柱较好地体现了“1+1>2”的拼合效应. 由表中试验力Pt3可知，随着螺钉间距增大，试件试验力呈下降趋势，畸变屈曲现象更明显且半波个数逐渐增多，由此说明螺钉间距增大，拼合效应减弱.

3   有限元分析

3.1   有限元模型建立

采用ABAQUS[17]有限元软件对CFS试件进行建模分析. CFS钢构件均采用S4R壳单元，ST4.8自攻螺钉采用C3D8实体单元，柱两端端板采用解析刚体. 钢材划分网格为5 mm × 5 mm，自攻螺钉网格为1 mm × 1 mm，有限元模型见图9.

试件的轴向位移由位于模型两端的参考点控制（见图9中RF1和RF2），参考点RF2在Uz方向的平动自由度为位移加载控制点. 在柱下端约束参考点RF2处的6个自由度（3个平动自由度和3个转动自由度）和约束柱上端参考点RF1处的除Uz外的5个自由度，以模拟柱两端固结的边界条件.

由于在试验过程中未观察到螺钉发生脱落和破坏的现象，因此有限元模型中自攻螺钉和拼合柱之间、试件端部与端板之间均采用Tie连接. 拼合翼缘之间建立面与面接触. 此外，为同时施加板件不平整度和试件初弯曲的初始缺陷，可根据Zhang等[18]的建议，在特征值分析时选择性地将试件板厚分别取为较小值t = 0.1 mm和较大值t = 10 mm，以便获得所需的局部屈曲模式和整体失稳模式. 随后对两个特征值分析文件进行拼合便可同时施加板件不平整度和试件初弯曲.

3.2   有限元模型验证

各试件有限元分析的承载力和破坏模式与试验结果对比见表3. 有限元分析得到的试件破坏特征与试验结果吻合较好. Pa和Pt分别是有限元和试验承载力，Pt /Pa的均值和方差分别为1.02和0.051，且两者的极限承载力也非常接近. 图10给出了部分试件有限元模型破坏模式与试验结果的对比，可看出有限元模拟的试件破坏模式和破坏位置与试验试件结果一致，说明本文有限元模型的准确性较好.

4   螺钉间距的影响规律

本文为研究螺钉间距对CFS拼合箱形柱畸变屈曲特性及承载力性能的影响规律，共设计3组畸变屈曲试件，试件几何尺寸见表4（D1中的D为畸变屈曲，1为试件编号;σl是局部屈曲临界应力;σd是畸变屈曲临界应力）. 本文螺钉间距以C形截面畸变屈曲临界应力对应的半波长（λc）为依据，取值分别为：0.5λc、0.7λc、0.9λc、1.1λc、1.3λc、1.5λc、2.0λc，以研究螺钉间距对畸变屈曲半波长的影响规律. 其中λc是C形截面畸变屈曲半波长，λc由CUFSM[15]得到. 此外，为判断畸变屈曲模式下CFS拼合箱形柱（如图11（b））的拼合效应，本文提出两种极限状态的假设模型：①C形和U形截面两单肢的极限强度之和作为下限值（如图11（a））;②拼合翼缘之间看作2t厚的整体截面柱的极限承载力作为上限值（如图11（c））.

有限元分析结果见表4、图12和图13，可得出以下结论：

1）由表4可知，随着螺钉间距增大，拼合箱形截面的极限承载力PFE1逐渐变小，但仍大于C形和U形两单肢截面立柱的极限承载力之和PFE2，且小于整体截面柱承载力PFE3. 同时，PFE1/PFE2、PFE1/PFE3的平均值分别是1.07、0.88，方差分别为0.061、0.073. 由以上可知，螺钉拼合柱的极限承载力介于两单肢之和与整体截面的极限承载力之间，说明螺钉约束作用对拼合箱形截面柱的受力性能具有一定的影响，但螺钉间距的变化对箱形截面拼合柱承载力影响并不是很大.

2）以D1试件为例，从图12可以看出，随着螺钉间距增大，螺钉间距小于0.9λc时，箱形截面试件的最大承载力大于C形和U形截面试件最大承载力之和，即1+1>2的拼合效应;螺钉间距大于0.9λc时，箱形截面试件的最大承载力逐渐接近C形和U形截面试件最大承载力之和，即1+1≈2，说明螺钉间距较大时对拼合截面柱的极限承载力影响很小且紧固作用很小. 同理，观察表4可知，D2和D3试件与D1试件有同样的结论. 因此，本文为拼合箱形截面的螺钉间距取值提供了参考依据，以减小螺钉间距对拼合箱形截面承载力的影响.

3）由图13可知，以D1试件为例，CFS拼合箱形截面柱的C形截面柱卷边带动翼缘仅有内缩现象，即畸变屈曲. 说明在螺钉约束的作用下，U形截面柱较好地控制了C形截面柱卷边外张口畸变的发展.

5   設计方法建议

由于目前没有明确的公式用于计算CFS拼合箱形柱的极限承载力，因此本文提出一种承载力计算方法，即用CUFSM软件计算得到C形和U形两单肢构件的屈曲临界荷载，再用直接强度法计算两单肢截面柱的极限承载力，运用承载力叠加法得到拼合箱形截面柱的畸变屈曲极限承载力. 其中计算屈曲临界荷载时，C形截面柱的有效长度取螺钉间距（e）与半波长λc的最小值，即L = min （λcrd，e）;U形截面有效长度为试件实际长度.

5.1   直接强度法

美国AISI规范中直接强度法（DSM）规定：轴压构件的极限承载力Pn = min（Pne，Pnl，Pnd），其中Pne、Pnl、Pnd分别为整体屈曲荷载、局部屈曲荷载和畸变屈曲荷载. 三种屈曲模式轴向荷载按下式计算.

1）整体屈曲：

Pne = 0.658■Py，λc ≤ 1.5;■Py，λc > 1.5.     （1）

2）局部屈曲：

Pn1=Pne，λ1 ≤ 0.776;1-0.15■■■■Pne，λ1 > 0.776.

（2）

3）畸变屈曲：

Pnd =Py，λd ≤ 0.561;1-0.25■■■■Py，λd > 0.561.

（3）

式中：Py = Ag fy，λ1 = ■，Pcrl = Ag fcrl，λd = ■，Pcrd = Ag fcrd，λc = ■;Pcre为弯曲屈曲荷载;Pcrl为局部屈曲荷载;Pcrd为畸变屈曲荷载;fy为屈曲强度;fcrl为局部屈曲临界应力;fcrd为畸变屈曲临界应力;Ag为构件截面的毛截面面积.

5.2   本文计算方法的验证

将本文方法计算结果分别与试验和有限元结果进行对比，结果如表3和表4、图14所示，可得以下几点：

1）观察表3和表4可知，试验结果（Pt3）和理论计算结果（PDSM）比值Pt3 /PDSM的平均值和方差分别为1.09和0.068，有限元结果（PFE）和理论计算结果（PDSM）比值PFE /PDSM的平均值和方差分别为0.97和0.064. 对比结果表明用直接强度法计算CFS箱形截面拼合柱畸变屈曲承载力稍偏保守，但方法可行.

2）由图14可知，对于CFS箱形截面拼合柱畸变屈曲的正则化长细比0.5 < λ < 3.0时，本文计算方法总体偏于保守，但与有限元结果相差不大，说明本文计算方法用于预测CFS箱形截面拼合柱的畸变屈曲承载力是可行的.

6   结   论

基于冷弯薄壁型钢拼合箱形截面轴压柱试验研究、数值模拟分析和计算理论对比分析，得出以下几点重要结论：

1）当畸变屈曲临界荷载Pcrd和局部屈曲临界荷载Pcrl满足Pcrd < Pcrl且Pud < Pcrl时，试件发生畸变屈曲.

2）CFS拼合箱形截面的畸变屈曲均发生于其组成构件C形截面，且C形截面翼缘和卷边一起发生内扣而无外张，此现象说明其组成构件U形截面能够对组成构件C形截面的外张起到约束作用，从而提高了CFS拼合箱形截面构件的屈曲后强度.

3）螺钉间距小于0.9λc时，拼合柱的极限承载力大于C形和U形截面柱极限承载力之和，此时畸变屈曲现象不明显;螺钉间距大于0.9λc时，拼合柱的极限承载力逐渐接近C形和U形截面柱极限承载力之和，畸变屈曲几乎均发生在两螺钉之间，且螺钉间距越大，畸变屈曲现象越明显且半波数越多. 结果表明螺钉布置对畸变屈曲CFS拼合箱形截面的承载力及畸变屈曲有一定的影响.

4）本文基于现行直接强度法提出了计算CFS拼合箱形柱畸變屈曲承载力的方法，将其计算结果分别与有限元和试验结果进行对比，本文方法稍微保守，但比较安全，证明了该计算方法的可行性及可靠性. 此外，进一步解决了CUFSM软件不能计算CFS拼合箱形截面弹性临界荷载的问题，为今后拼合截面的设计应用提供了很好的借鉴.

参考文献

[1]    LAU S C W，HANCOCK G J. Distortional buckling formulas for channel columns[J]. Journal of Structural Engineering，1987，113（5）：1063—1078.

[2]    KWON Y B，HANCOCK G J. Tests of cold-formed channels with local and distortional buckling[J]. Journal of Structural Engineering，1992，118（7）：1786—1803.

[3]    管宇，周绪红，石宇，等. 轻钢组合楼盖面内刚度和承载力计算方法研究[J]. 湖南大学学报（自然科学版），2019，46（9）：31—43.

GUAN Y，ZHOU X H，SHI Y，et al. Study on calculation method for in-plane stiffness and bearing capacity of thin-walled steel composite floor[J]. Journal of Hunan University （Natural Sciences），2019，46（9）：31—43. （In Chinese）

[4]    YOUNG B，CHEN J. Design of cold-formed steel built-up closed sections with intermediate stiffeners[J]. Journal of Structural Engineering，2008，134（5）：727—737.

[5]    ZHANG J H，YOUNG B. Experimental investigation of cold-formed steel built-up closed section columns with web stiffeners[J]. Journal of Constructional Steel Research，2018，147：380—392.

[6]   AISI North American specification for the design of cold-formed steel structural members：AISIS100-16[S]. Washington DC：American Iron and Steel Institute，2007：7—8.

[7]    李元齐，姚行友，沈祖炎，等. 高强冷弯薄壁型钢抱合箱形截面受压构件承载力试验研究[J]. 建筑结构，2011，41（6）：36—41.

LI Y Q，YAO X Y，SHEN Z Y，et al. Load-carrying capacity of 550 MPa high-strength cold-formed thin-walled steel built-up box section columns[J]. Building Structure，2011，41（6）：36—41. （In Chinese）

[8]    冷弯薄壁型钢结构技术规范：GB 50018—2002 [S]. 北京：中国计划出版社，2002：19—20.

Technical specification for cold-formed thin-walled steel structures：GB50018—2002 [S]. Beijing：China Planning Press，2002：19—20. （In Chinese）

[9]    袁涛涛.闭合多肢冷弯薄壁型钢拼合截面立柱轴压承载力试验与理论研究[D]. 西安：长安大学，2010：1—91.

YUAN T T. Experimental and theoretical research on bearing capacity of closed-section multi-limbs built-up cold-formed steel compression columns[D]. Xian：Changan University，2010：1—91. （In Chinese）

[10]  李方涛. 冷弯薄壁型钢双肢抱合箱形截面柱轴向受力性能研究 [D]. 西安：长安大学，2015：1—110.

LI F T. Study on the axial mechanical properties of cold-formed thin-walled steel built-up box-section columns [D]. Xian：Changan University，2015：1—110. （In Chinese）

[11]  聂少锋，周天华，袁涛涛，等. 冷弯薄壁型钢拼合箱形截面立柱轴压性能试验研究[J]. 土木建筑与环境工程，2012，34（4）：46—52.

NIE S F，ZHOU T H，YUAN T T，et al. Experimental analysis on behavior of cold-formed steel box built-up section columns under axial compression[J]. Journal of Civil，Architectural & Environmental Engineering，2012，34（4）：46—52. （In Chinese）

[12]  NING K Y，YANG L，YUAN H X，et al. Flexural buckling behaviour and design of welded stainless steel box-section beam-columns[J]. Journal of Constructional Steel Research，2019，161：47—56.

[13]  DAR M A，SAHOO D R，JAIN A K. Axial compression behavior of laced cold-formed steel built-up columns with unstiffened angle sections[J]. Journal of Constructional Steel Research，2019，162：105727.

[14]  徐克龍，施刚，林错错. 960MPa高强度钢材轴压柱局部稳定性能及设计方法[J]. 湖南大学学报（自然科学版），2017，44（1）：102—111.

XU K L，SHI G，LIN C C. Analysis and design method on local buckling behavior of 960 MPa high strength steel columns under axial compression[J]. Journal of Hunan University （Natural Sciences），2017，44（1）：102—111. （In Chinese）

[15]  SCHAFER B W. CUFSM4.05-finite strip buckling analysis of thin-walled members [M]. Baltimore：Department of Civil Engineering，Johns Hopkins University，2012：1—84.

[16]  金属材料拉伸试验 第1部分：室温试验方法 GB/T 228.1—2010[S]. 北京：中国标准出版社，2011.

Metallic materials - Tensile testing—Part 1：Method of test at room temperature：GB/T 228.1—2010[S]. Beijing：Standards Press of China，2011.（In Chinese）

[17]  江丙云，孔祥宏，罗元元. ABAQUS工程实例详解[M]. 北京：人民邮电出版社，2014：28—181.

JIANG B Y，KONG X H，LUO Y Y. Detailed explanation of ABAQUS project example [M]. Beijing：Posts and Telecom Press，2014：28—181. （In Chinese）

[18]  ZHANG J H，YOUNG B. Numerical investigation and design of cold formed steel built-up open section columns with longitudinal stiffeners[J]. Thin-walled Structures，2015，89：178—191.