基于不同火源位置的分岔隧道临界风速数值研究

苏 毅，曾艳华

基于不同火源位置的分岔隧道临界风速数值研究

苏 毅1，曾艳华2

（1. 山西静兴高速公路有限公司，山西 吕梁 033500；2. 西南交通大学，交通隧道工程教育部重点实验室，成都 610031)

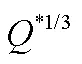
分叉隧道；火源位置；分岔角度；烟气逆流长度；临界风速

0 引 言

临界风速是使隧道火灾烟气不往火源上游扩散时的最小纵向风速，此时烟气逆流长度为零。针对临界风速各国学者做了大量研究：Oka[1]和Li[2]等人通过模型试验系统地进行了隧道烟气运动研究，发现在较低的热释放速率下，无量纲临界风速随无量纲热释放速率的三分之一幂而变化，而在较高的无量纲热释放速率下，无量纲临界速度几乎与无量纲热释放速率无关。Weng[3]和Wu[4]等人考虑隧道截面对临界风速的影响，通过模型试验与数值模拟得出了临界风速半经验公式。Gwon[5]和Yi[6]等人利用模型试验研究了隧道坡度对临界风速的影响，总结出有坡度临界风速与无坡度临界风速之间的关系。Kang[7]和Lee[8]等人考虑堵塞率对临界风速的影响而进行了数值模拟，发现临界风速随阻塞率的增大而减小。Zhong[9]等人利用模型隧道研究了不同横向火灾位置对纵向通风速度抑制隧道火灾烟气回流的影响，研究指出：当火源在隧道中心时，临界风速模型与Wu[4]等人提出的模型相似；当火源与隧道侧壁间距减小时，临界风速呈指数增长。Tang[10]等人研究了车辆堵塞与火源的相对距离对临界风速的影响，引入无量纲系数来考虑车辆堵塞与火源相对距离对临界风速的影响，提出新的临界风速计算公式。Zhang等人[11]研究了弧形隧道半径与临界风速之间的关系，结合理论分析与CFD数值模拟总结出了考虑弧形隧道无量纲半径的临界风速计算公式。

当前针对普通单管直线隧道的临界风速研究已很完善。然而，修建多匝道城市地下隧道已成为缓解城市中心区主干道交通拥堵、缩短城市区间道路里程的主要手段之一。多节点隧道在结构形式上存在着隧道的汇合与分岔，火灾烟气的迁移规律及对火灾烟气的控制势必与普通单管直线隧道不同。对于分岔隧道，李俊梅[12]等人研究了无纵向通风条件下不同分岔角度对分岔隧道烟气迁移的影响发现：分岔角度对烟气逆流长度影响很小，但对火源下游主、支路隧道内的烟气蔓延有一定影响；分岔隧道的烟气质量流量分配比例随分岔夹角的增大逐渐减小，但总体变化幅度很小。

当前有关分岔隧道临界风速的研究还不够深入，未能建立一个统一的临界风速计算模型。因此，深入地研究分岔隧道临界风速的有关规律就很有必要。本文基于FDS研究火源位置与分岔角度对分岔隧道临界风速的影响，结合量纲分析与线性拟合推导出分岔隧道临界风速计算模型，所得结果能为分岔隧道通风设计提供参考。

1 数值模拟

1.1 模型隧道

主隧道宽10m、高5m，匝道宽7.5m、高4.5m。隧道总长300m，分岔点前主隧道长180m，连拱长20m，分岔点后主隧道长100m，匝道长100m，如图1所示。隧道建筑结构为热厚型，材料为混凝土。火源大小长宽分别为6m×2m，火源位于主隧道中心线上，产烟量为0.03 kg/kg。隧道入口设置为“SUPPLY”边界条件，为隧道中提供不同大小的纵向风速，主隧道及匝道出口设置为开放边界条件。在整个模拟过程中，环境温度和压强分别设定为20℃和101kPa，计算时间为600s。此外，在隧道顶部以下0.2m处布置了一系列间隔为0.3m的热电偶来监测隧道拱顶温度分布。

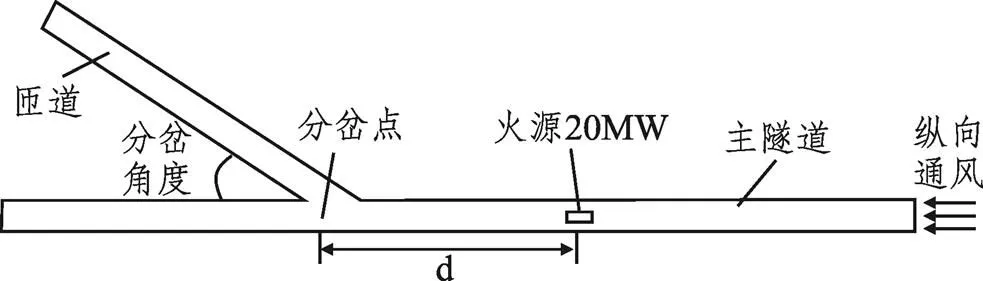
图1 模型隧道示意

1.2 网格划分

FDS模拟首先需要仔细考虑的关键参数是计算网格的大小，因为它对FDS模拟结果的精度起着重要作用。Mcgrattan[13]等人发现当网格尺寸大约为0.1倍火源特征直径时，模拟结果的精度是可以接受的，火源特征直径可按下式计算：

在FDS模拟中，火源热释放速率为20 MW时按式（1）计算的网格大小为3.80m，0.1*即为0.38m。为了使计算结果更加可靠，本文的数值计算模型的网格尺寸选择0.20 m。

1.3 计算工况

本文将着重研究分岔角度为20°和60°这两种情况下火源与分岔点之间的距离对分岔隧道临界风速的影响。火源热释放速率设为定值20MW，距离分别为-25m、0m、25m、50m和75m（正值表示分岔点之前，负值表示分岔点之后）。其他相关参数如表1所示。

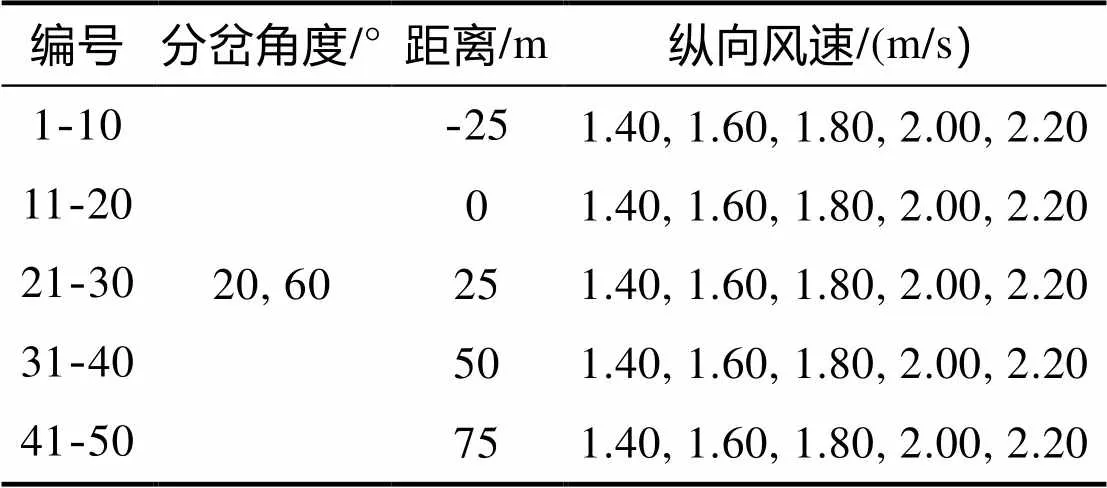
表1 FDS模拟方案

2 量纲分析

一般来说火源附近顶棚温度最高，逆行烟气在蔓延时温度会不断降低，与机械送风冷气流交锋形成一个冷热锋面，前锋面温度陡降。温度陡降处与火源之间的距离即为逆流长度[14]，烟气逆流长度为0时的纵向风速即为临界风速。因此，在研究临界风速之前首先需要得到烟气逆流长度与纵向风速的关系。Li[2]等人发现影响烟气逆流的主要因素有：火源热释放速率、纵向风速、特征水力高度、空气密度、环境温度、空气比定压热容和重力加速度，具体可表示为：

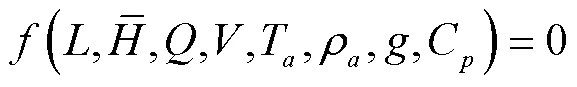
将式（1）无量纲化得到下式：

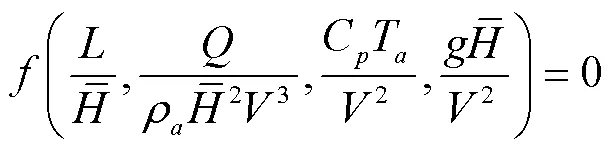
根据相似理论由式（3）可得：

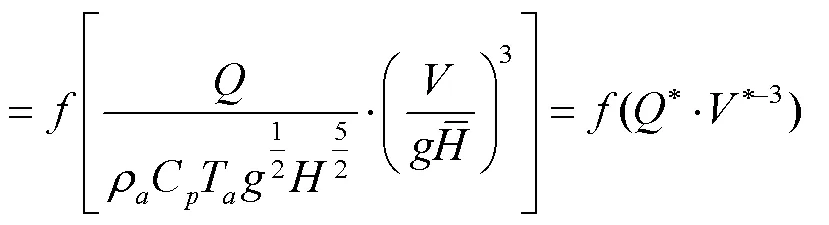
即：

3 结果与分析

3.1 20°分岔无量纲逆流长度

对数值模拟结果进行处理得到不同距离及纵向风速下的烟气逆流长度，如表2所示。为了得到无量纲风速与无量纲逆流长度之间的函数关系，首先对表2数据进行无量纲化处理，如图

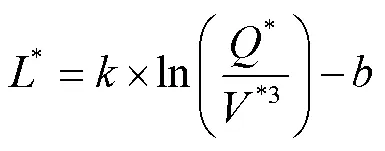
表2 隧道烟气逆流长度

斜率与截距随着火源与分岔点之间的距离增大而增大，说明斜率与截距与距离也存在某种关系。由于式（6）是无量纲表达式，为了将火源与分岔点之间的距离考虑进去，现定义无量纲火源与分岔点距离：

通过对计算结果进行拟合，可得出出斜率k、截距b与无量纲火源与分岔点距离的关系，如图3所示。

对于斜率：

对于截距：

将式（8）、（9）代入式（6）整理得：

3.2 60°分岔无量纲逆流长度

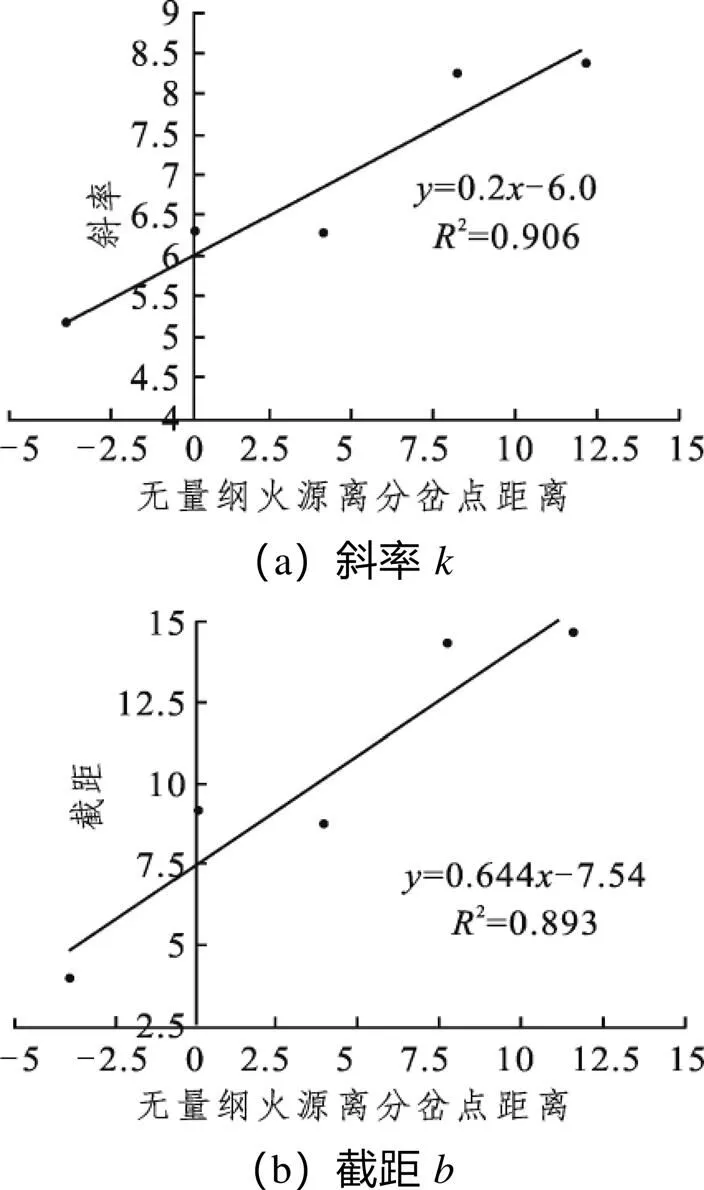
图4 斜率和截距与无量纲火源离分岔点距离的关系

对于斜率：

对于截距：

将式（11）、式（12）代入式（6）整理得：

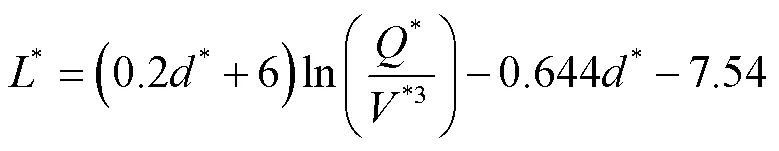
3.3 临界风速

当烟气逆流长度为零时所对应的纵向风速即为临界风速，令式（6）无量纲逆流长度为零，整理得：

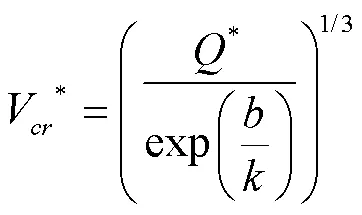
将式（9）～（12）代入式（14）整理得：

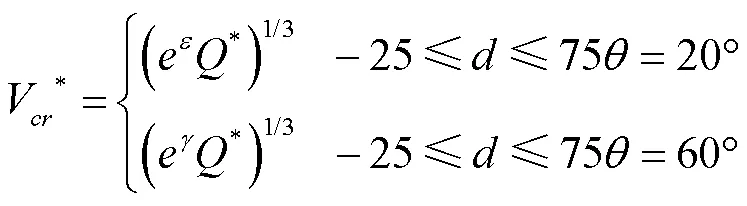
式中：

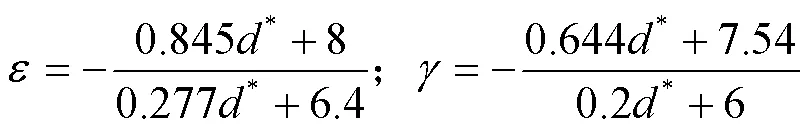
3.4 对比分析

表3 无量纲临界风速计算结果（）

对于斜率：

对于截距：

将式（16）、（17）代入式（6）、式（14）得到不考虑分岔角度的无量纲烟气逆流长度和无量纲临界风速计算公式：

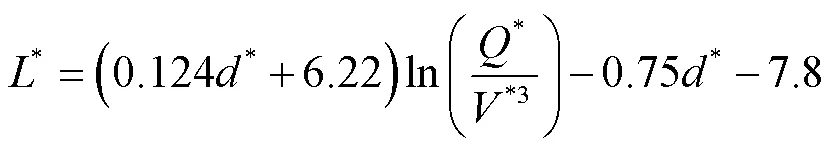
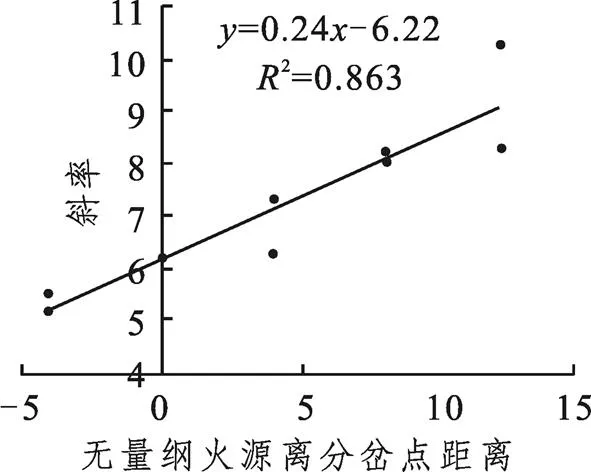
图5 不同分岔角度下斜率与无量纲距离的关系

图6 不同分岔角度下截距与无量纲距离的关系

表4 临界风速模拟值与预测值对比（)

4 结束语

（1）无量纲烟气逆流长度和无量纲火源热释放速率及无量纲纵向风速有一定的函数关系，通过对模拟结果分析得出考虑不同分岔角度及火源位置的无量纲烟气逆流长度和无量纲临界风速计算公式。

（4）火源在分岔点之后的无量纲临界风速与单管直线隧道相比差距不大；当火源在分岔点之前时，单管直线隧道的无量纲临界速度比分岔隧道高23%～37%。

（5）将两种分岔角度的无量纲临界风速对比分析发现：不同分岔角度、相同火源位置下的无量纲临界风速相差不大，在误差允许范围内得到了不考虑分岔角度的无量纲临界风速半经验计算公式。

[1] OKA Y, ATKINSON G T. Control of smoke flow in tunnel fires[J]. Fire Safety Journal, 1995, 25: 305-322.

[2] LI Y Z, LEI B, INGASON H. Study of critical velocity and back-layering length in longitudinally ventilated tunnel fires[J]. Fire Safety Journal, 2010, 45: 361-370.

[3] WENG M C, LU X L, LIU F, et al. Study on the critical velocity in a sloping tunnel fire under longitudinal ventilation[J]. Applied Thermal Engineering, 2016, 94: 422-434.

[4] WU Y, BAKAR M. Control of smoke flow in tunnel fires using longitudinal ventilation systems—a study of the critical velocity[J]. Fire Safety Journal, 2000, 35: 363-390.

[5] GWON H K, SEUNG R K, HONG S R. An experimental study on the effect of slope on the critical velocity in tunnel fires[J]. Journal of Fire Science, 2009, 28: 27-47.

[6] YI L, XUQ Q, XU Z S, et al. An experimental study on critical velocity in sloping tunnel with longitudinal ventilation under fire Tunnel [J]. Tunnelling and Underground Space Technology, 2014, 43: 198-203.

[7] KANG K. Characteristic length scale of critical ventilation velocity in tunnel smoke control[J]. Tunnelling and Underground Space Technology, 2010, 25: 205-211.

[8] LEE Y P, TSAI K C. Effect of vehicular blockage on critical ventilation velocity and tunnel fire behavior in longitudinally ventilated tunnels[J]. Fire Safety Journal, 2012, 53: 35-42.

[9] ZHONG W, LI Z Z, WANG T, et al. Experimental study on the influence of different transverse fire locations on the critical longitudinal ventilation velocity in tunnel fires[J]. Fire Technology, 2015, 51 (5): 1217-1230.

[10] TANG W, HU L H, CHEN L F. Effect of blockage-fire distance on buoyancy driven back-layering length and critical velocity in a tunnel: an experimental investigation and global correlations [J]. Applied Thermal Engineering, 2013, 60 (1-2): 7-14.

[11] ZHANG S G, YANG H, YAO Y Z, et al. Numerical investigation of back-layering length and critical velocity in curved subway tunnels with different turning radius [J]. Fire Technology, 2017, 53 (5): 1765-1793.

[12] 李俊梅, 刘闪闪, 许鹏, 等. 分岔角对地下道路火灾烟气蔓延影响模拟[J]. 消防科学与技术, 2014, 33 (6): 616-618.

[13] MCGRATTAN K, MCDERMOTT R, HOSTIKKA S, et al. Fire dynamics simulator (Version 5）user’s guide[M]. Gaithersburg: National Institute of Standards and Technology, 2010: 37-41.

[14] 李颖臻, 雷波. 隧道火灾模型试验中列车对烟气控制的影响[J]铁道学报, 2010, 32 (5): 136-139.

[15] WENG M C, LU X, LIU F, DU C. Study on the critical velocity in a sloping tunnel fire under longitudinal ventilation[J]. Applied Thermal Engineering, 2016, 94: 422-434.

Numerical Study on Critical Velocity of Bifurcated Tunnel Based on Different Locations of Fire Sources

SU Yi1, ZENG Yan-hua2

(1. Shanxi Jingxing Expressway Co., Ltd., Lvliang 033500, China; 2. Key Laboratory of Transportation Tunnel Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu 610031, China）

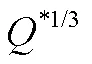
bifurcated tunnel; fire-source position; bifurcation angle; smoke back-layering length; critical velocity

1672-4747（2021）03-0076-07

U458.1

A

10.19961/j.cnki.1672-4747.2020.09.010

2020-09-23

2020-11-19

2021-05-07

国家重点研发计划课题（2016YFC0802201）

苏毅（1982—），男，辽宁锦州人，主要从事公路与铁路工程施工技术应用与研究，E-mail：suyimail@163.com

曾艳华（1968—)，女，四川成都人，博士，教授，主要从事隧道通风与防灾方面的研究，E-mail：zengyhua@163.com

苏毅，曾艳华. 基于不同火源位置的分岔隧道临界风速数值研究[J]. 交通运输工程与信息学报, 2021, 19(3): 76-82.

SUYi, ZENG Yan-hua. Numerical Study on Critical Velocity of Bifurcated Tunnel Based on Different Locations of Fire Sources [J]. Journal of Transportation Engineering and Information, 2021, 19(3): 76-82.

（责任编辑：刘娉婷）