基于近邻和SVM的公交停靠时间预测

霍 豪，郑长江，沈金星

基于近邻和SVM的公交停靠时间预测

霍 豪，郑长江，沈金星

（河海大学，土木与交通学院，南京 210098）

为提高公交行程时间预测的准确性，提升公交系统的整体服务水平，提出了一种公交车站点停靠时间预测模型。在考虑上下车人数、在车人数和天气状况等因素对公交停靠时间的影响下，采用训练集样本预筛选操作，分析样本筛选过程中不同抽样率对预测效果的影响，比较基于不同核函数的支持向量机在预测精度上的差异。选取佛山市301路公交线中有代表性的10个站点，用以检验基于近邻的支持向量机模型的预测效果，并分析不同站点的特性。试验结果表明，所提出的模型可以达到较高的预测精度，决定系数为0.4255，均方根误差为9.4737，且计算时间与不进行预筛选时相比，降低约40%。训练集数据的预筛选过程可以缩短模型的计算时间并且降低预测误差，而基于线性核函数的支持向量机比基于其他核函数的预测效果更好。

交通工程；预测模型；支持向量机；停靠时间；城市公交

0 引 言

在城市公共交通中，公交停靠时间对于评价公交系统的服务水平和服务质量[1, 2]，以及分析交通网络的稳定性[3, 4]，均具有重要作用。从定量的角度，在客流量和发车频率都较高的公交线路上，公交停靠时间占总行程时间的比例甚至达到26%[5]。可见，准确预测公交停靠时间对于合理有效地制定公交运行时刻表，提高公交出行的服务质量和吸引力具有重要意义。

公交停靠时间是指公交车为服务乘客而在公交站点处于静止状态的时间段长度，包括乘客上下车以及车辆开关门时间，是公交车辆行程时间的重要组成部分[6]。目前，已有多种方法被应用于公交停靠时间的预测中，Bertini等[7]基于上下车人数，提出了一种计算站点停靠时间的线性模型，作为预测行程时间的一部分。Jaiswal等[8]考虑了BRT车站站台拥挤度和乘客在站台的行走时间对车辆停靠时间的影响。Meng等[9]考虑了公交车在港湾式公交站停靠过程中，车辆、候车乘客和路肩车道上的交通状况三者之间相互作用所产生的随机性对停靠时间的影响，并使用标准再生随机过程对这种随机性的概率分布进行模拟，取得了较好的预测效果。杨敏等[10]利用支持向量机（Support Vector Machine，SVM）在解决非线性回归问题上的优势，以及差分自回归移动平均法（Autoregressive Integrated Moving Average，ARIMA）能体现停站时间的纵向时间相关性的特点，将两种方法相结合对公交停靠时间进行预测，发现相较于单一的ARIMA模型或SVM模型，组合模型预测的平均相对百分误差和均方误差都有明显降低。Bie等[6]研究了车内拥挤度对公交停靠时间的影响，发现相比于仅考虑上下车人数的停靠时间预测模型，加入拥挤度之后，预测的平均绝对误差降低了137.51%。

交通系统复杂的内在联系会造成公交停站时间的不确定性，这种不确定性很难用单纯的线性模型进行拟合。现有文献中对于公交运行时段的划分往往根据经验（如将早高峰时段定义为7：00～ 9：00），而没有依据实际运行数据进行统计分析，这可能会造成数据状态的划分不准确；在考虑影响公交停靠时间的因素时，大多考虑的是交通内部因素，而对于天气等影响乘客上下车过程的外部因素考虑较少。本文根据公交运行实际数据分析了客流的时间分布规律，并考虑天气因素对停靠时间的影响。SVM模型中核函数的选取对于模型的训练和最终的预测效果有重要影响，而以往的研究中[10, 11]，作者往往依据经验选择某一核函数，没有根据实际数据进行试验和比较，这可能造成所选择的核函数并非为特定数据条件下的最佳核函数，所以本文在运用SVM算法对历史数据进行训练时，比较了不同核函数的预测效果。此外，SVM具有适合小样本预测的特性，为了解决其在样本量过大的情况下训练时间过长的问题，引入了训练集样本预筛选的过程。基于以上改进，本文提出一种新的公交停靠时间预测模型，并使用佛山市301路公交车辆的实际运营数据对模型进行验证。

1 公交停靠时间预测模型

1.1 支持向量机

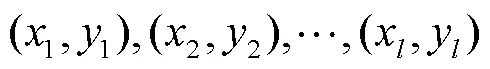
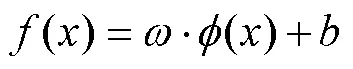
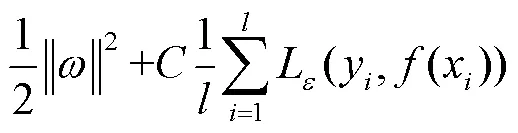
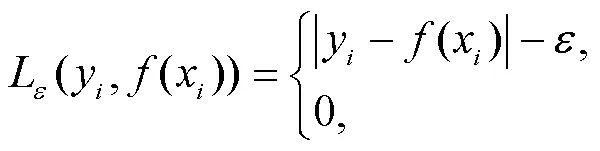
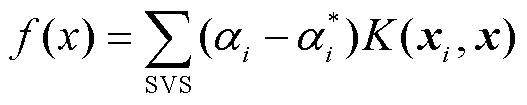
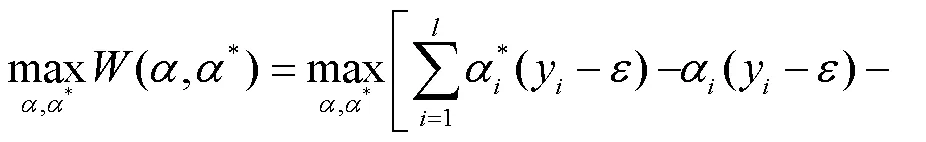
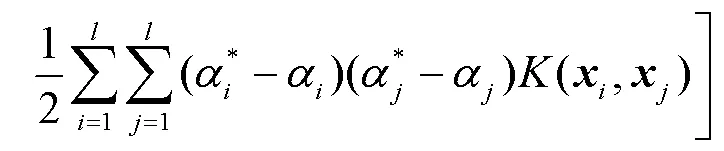
s.t.

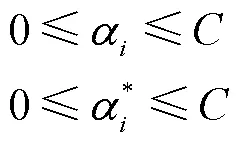
支持向量机基于结构风险最小化原则，以最小化由训练误差和置信水平组成的泛化误差的上界为目标，这是与经验风险最小化原则的区别，后者只是将训练误差最小化。基于这一原理，SVM在解决许多机器学习问题时，通常比采用经验风险最小化原则的方法具有更强的泛化能力。它的另一个关键特征在于，训练SVM等价于求解一个线性约束的二次规划问题，因此它的解总是唯一且全局最优的，而不是像神经网络那样需要非线性优化，且具有陷入局部极小的危险。在SVM中，问题的解决只依赖于训练数据点的子集，这些数据点被称为支持向量（Support Vector）。仅使用支持向量，可以得到与使用所有训练数据点相同的解。但SVM的一个缺点在于，相对于训练样本的数量，它的训练时间介于二次到三次之间。因此，当使用SVM解决大数据量的问题时，计算时间将会非常长[12]。

1.2 基于近邻的SVM模型

大规模的数据能够为机器学习的过程提供更多有用的信息，更全面地揭示特征之间的内在关联，但同时，随着数据量的增大，与预测目标关联性不强的数据也会增加，这会对预测模型的精度造成负面影响。

为了解决SVM在处理大数据量问题时训练时间过长的问题，同时提高训练数据与预测目标的关联性，本文提出了基于近邻的支持向量机（Support Vector Machine Based on Near Neighbors, SVMNN）预测模型。其包含两个主要的过程：第一阶段，用近邻法对原始的训练集数据进行预筛选；第二阶段，运用SVM算法对筛选后的数据进行训练和回归预测。

首先，训练集预筛选的目的是减少数据量，同时提高数据质量。数据质量可由训练集和预测数据之间的相似度来衡量，而相似度通常由被比较对象在数据特征方面的距离来进行数值度量，训练集数据与预测数据的距离越小，则相似度越高，其数据质量就越高。对于连续型变量，一种常用的距离度量方法是欧氏距离，本文即采用这一方法，公式为：

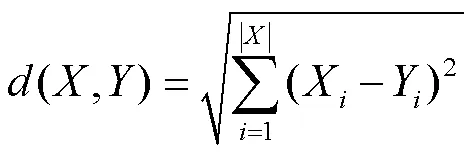
对于训练集中的每一个样本，计算其与测试集样本的距离值（当测试集有多个样本时，取平均值），再用下式计算得到每一个训练集样本被选择的概率[14]：

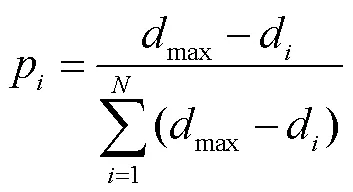
将训练集样本与预测样本的相似度作为适应度，用轮盘赌方法对预测模型的输入样本进行筛选。如图1所示，其中1是与非常相似的样本（欧式距离值非常小，被选择的概率很大），因此1比2和3被选择作为训练集样本的概率更高。

图1 用轮盘赌方法对不同相似度的训练样本进行筛选

第二阶段，用SVM算法对第一阶段筛选出的训练集样本进行训练，得到公交停靠时间预测模型，对测试样本进行预测。

1.3 模型评价指标

为了验证SVMNN模型的预测效果，本文使用两个指标对模型进行评价：决定系数（2）和均方根误差（）。2反映了回归贡献的相对程度，即在因变量的总变异中，回归关系所能解释的百分比，用来度量未来的样本是否可能通过模型被很好地预测。2为1表示最好，其值越大（接近于1），表明所拟合的回归方程越优。RMSE反映真实值与预测值的偏离程度，其值越小，说明预测误差越小，预测越准确。这两个指标的计算方法如下：

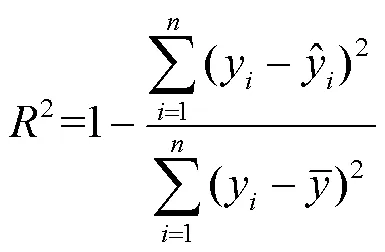
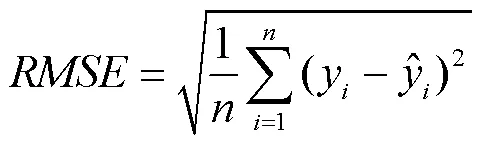
2 数据介绍和处理

2.1 数据介绍

本文采用佛山市301路公交在2019年12月1～31日的站点停靠数据，数据字段包括：日期、线路名称、线路方向、站点序号、到站时间、滞站时间、离站时间、上车人数、下车人数、在车人数。此外，通过网络爬虫技术，可以获取佛山市2019年12月1～31日的天气信息。以上字段中，“滞站时间”字段对应的数据即为模型的输出。

2.2 数据状态划分

城市道路交通运行状态受时段的影响较大，工作日和非工作日、高峰期和平峰期的客流状况有着明显不同[15]，这会导致公交车的停靠时间出现差异，所以预测公交停靠时间，应将工作日和非工作日分别考虑，并根据客流数据的统计分析，对公交车的运行时段进行划分。佛山市301路公交下行方向（顺德工业园总站—新滘）客流的统计结果如图2所示（其中，横坐标“6”对应的点代表6:00～7:00之间301路公交下行方向在2019年12月工作日或非工作日上车总人数的平均值，后面依此类推）。

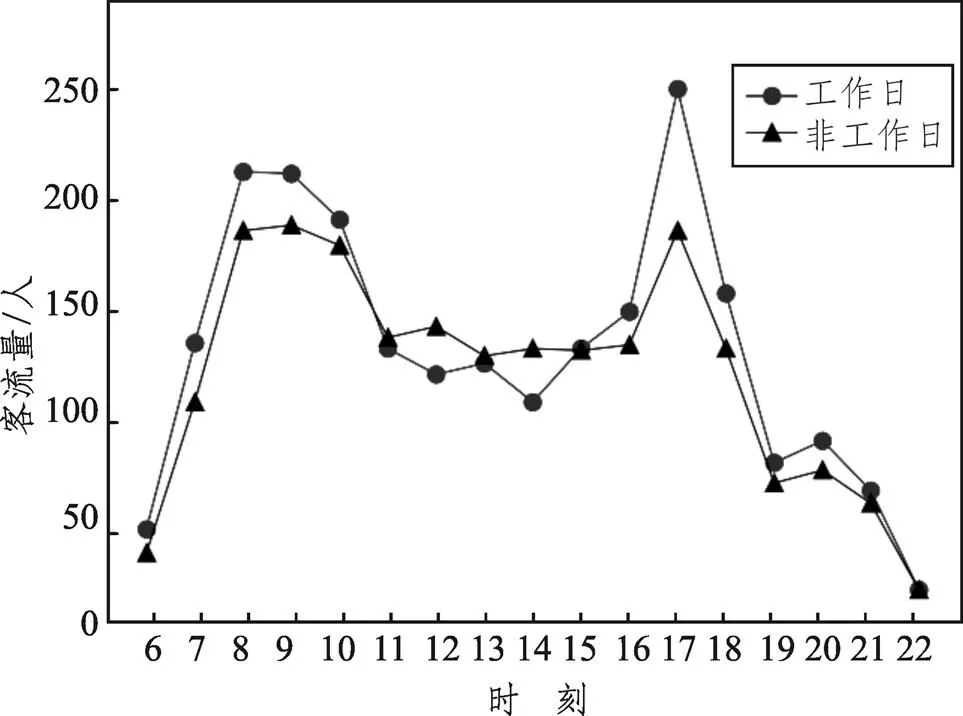
图2 公交客流时间分布图

根据图2的统计结果，可以将该公交线路的运行时段划分为3类，如表1所示。

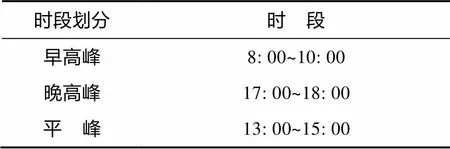
表1 公交车运行时段划分

2.3 特征数据获取和处理

公交车停靠时间的影响因素主要有上下车人数、车内拥挤度、天气状况等。其中，大量研究表明，上下车人数是影响停靠时间的最重要因素[16, 17]。Bie等[6]则专门研究并证明了车内拥挤度对公交停靠时间的重要影响。而天气状况因素，包括是否下雨、风速值等，会影响乘客上下车的流率。例如，在下雨天，乘客上下车的过程伴随着收伞和撑伞的过程，上下车流率会大大降低，而在现有的公交停靠时间预测研究中，似乎未见有考虑天气因素的影响。

本文选取了上下车人数特征、在车人数特征和天气特征数据，以此作为模型的输入，加入到模型的训练过程中。部分天气数据如表2所示，其中，H_temp代表当日最高温，L_temp代表当日最低温，weather代表当日天气状况，wind代表风向和风速。观察数据可发现，在该月，佛山市未出现雨天，故本文以“是否为晴天”对天气状况数据做二分处理（晴天为1，非晴天为0），由于该特征对应的值为类别型变量，故进而对其进行独热编码，以便做回归预测；当月最高气温和最低气温十分稳定，故H_temp和L_temp不作为输入特征；风速值对乘客的行动过程会造成影响，故作为特征信息加入特征序列。

表2 佛山市天气信息

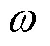
3 实例分析

3.1 不同样本筛选率和SVM核函数的比较

选取不同的训练集样本筛选率和SVM核函数对模型进行标定，得到数据试验结果如图3所示。试验中选用的是301路公交在2019年12月所有工作日早高峰的下行方向站点停靠数据，共9 857条数据，将其中的80%（共7 885条）作为训练集，20%（共1972条）作为测试集。

从图3（a）可以看出，linear核函数在不同筛选率下都取得了3种核函数中最大的2值，且在筛选率为0.75时取得最大值，为0.425 5；图3（b）中，linear核函数在不同筛选率下都取得了3种核函数中最小的值，且在筛选率为0.75时取得最小值，为9.473 7。

综上所述，进行训练集数据的预筛选能够提高模型的预测精度，不仅如此，数据量的减少有助于缩短模型训练时间，从而提高预测效率。在训练数据预筛选阶段使用0.75的抽样率，在模型训练阶段使用linear核函数的SVM模型，可以取得最好的预测效果，本文即以这两个取值对预测模型进行标定。

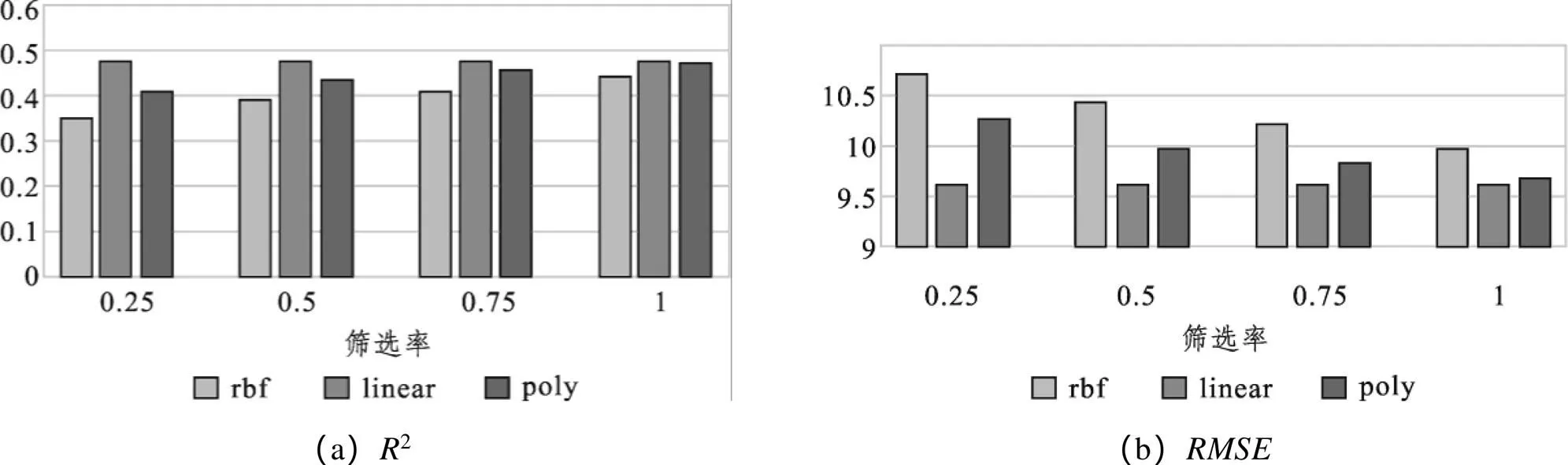
图3 不同核函数和筛选率下的预测结果

3.2 不同预测模型的比较

现将SVMNN模型与原始SVM模型的预测结果和计算时间进行对比，结果如表3所示。

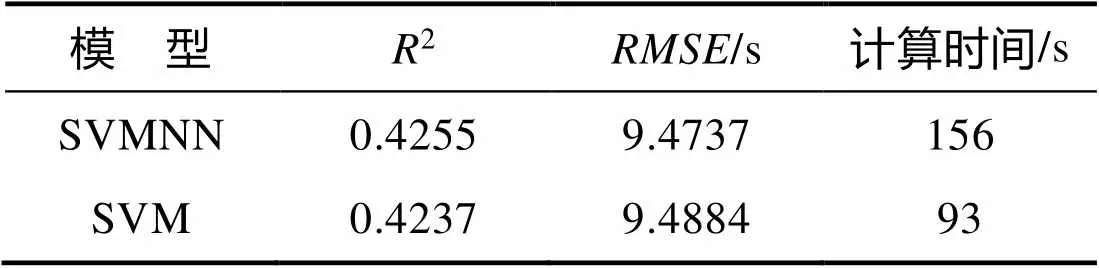
表3 不同模型的性能表现

针对表3中的结果进行分析，可发现，SVMNN模型在2和两项评价指标上均优于SVM模型，其中，2提升了0.0018，降低了0.0147，这说明对训练数据的预筛选能够提高SVM模型的准确率，降低其预测误差，也验证了SVM模型在处理小样本问题时更具优势。模型的计算环境为6核2.6GHz处理器、16GB RAM，通过对比模型的计算时间可发现，SVMNN的计算时间远短于SVM，降低了约40%，因为SVMNN经过数据的预筛选，其训练集的样本量只有SVM模型的75%，更少的训练数据能带来更短的模型计算时间。同时，被筛选出来的数据是与待预测样本高度相似的数据，所以在缩短计算时间的同时，SVMNN模型还具备更好的预测效果。

3.3 不同站点预测结果比较

选择佛山市301路公交线中，在用地性质、周围环境等方面具有代表性的10个站点，用已标定好的模型对这些站点分别进行公交停靠时间预测，比较不同性质的站点在不同时间段的预测结果。其中，WP（workday & peak period）代表工作日早高峰，WO（workday & off-peak）代表工作日平峰，NP（non-work day & peak period）代表非工作日早高峰，NO（non-work day & off-peak period）代表非工作日平峰。试验结果如图4所示。

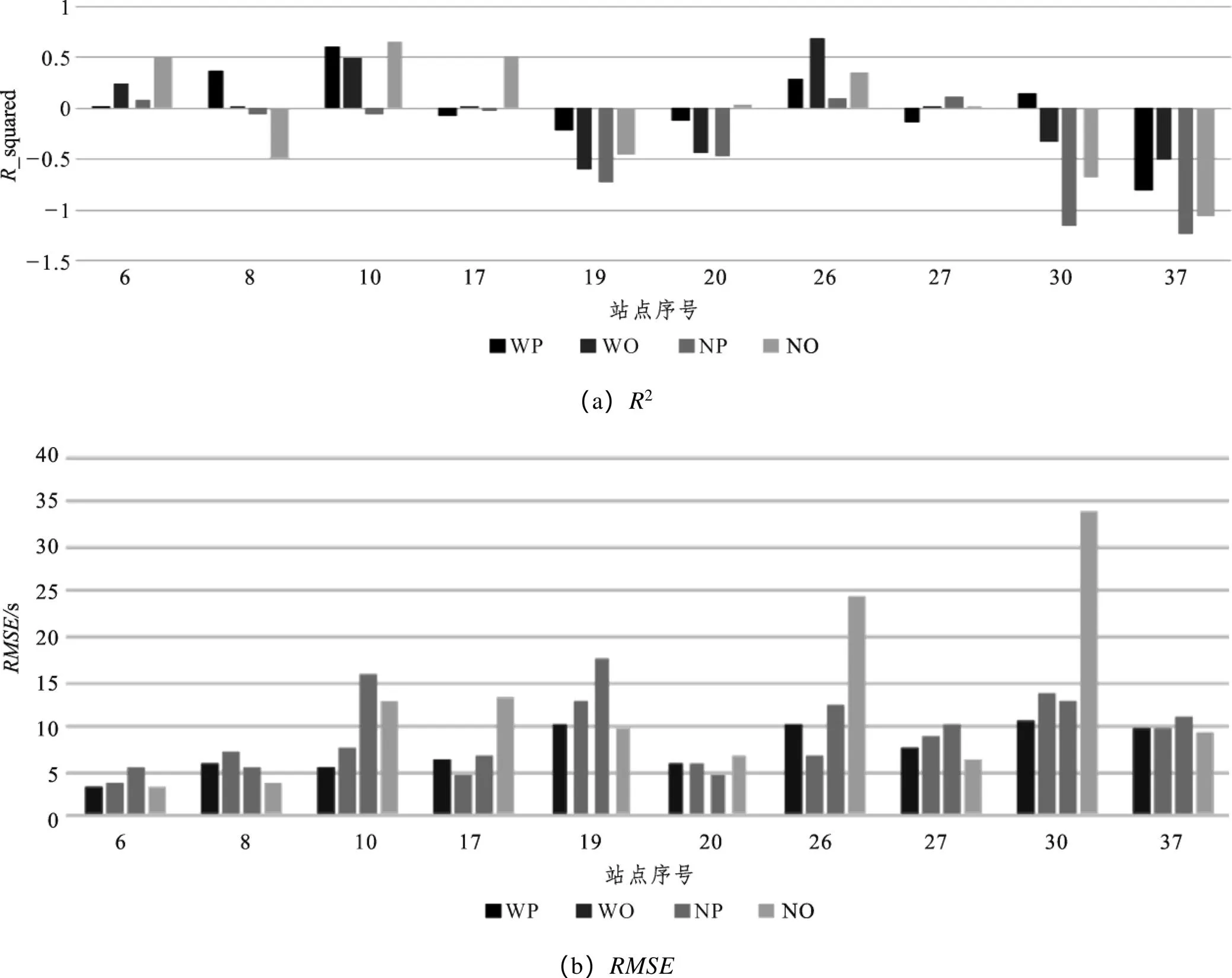
图4 不同站点和不同时间段的预测结果

从图4（a）可以看出，第6站（欧洲工业园路口）和第10站（顺德职院）的2值较高，这是因为第6站位于工业区，第10站位于学校区域，这两个区域的公交客流规律性比较强，所以预测准确率比较高。而第30站（清晖园）和第37站（区疾控中心）2值较低，其中第30站位于风景区，客流量不规律，尤其在非工作日，人流量比较大，预测难度更高，正如图中所示，NP和NO对应的2非常低；第37站位于医院附近，人流量非常大，尤其在非工作日。从图中可见，在4类时间段内，2均为负值，预测效果很不理想，尤其在NP和NO两个非工作日状态下，2甚至低于-1。

从图4（b）中可以看出，第6站和第8站（丰田合诚配件厂）的最低，因为这两个站点均位于工业区，通勤客流量比较大，上下车乘客的时间规律性比较强，预测难度较小。而第26站（美食城）和第30站在非工作日平峰期的值非常高，其中第26站位于商业区、第30站位于风景区，在非工作日平峰期出门购物和游玩的人流量相对较高，增加了预测的难度。

4 结 论

本文设计了一种基于近邻和SVM的公交停靠时间预测模型，其中近邻的作用在于提前筛选出与待预测样本相似度较高的历史样本，SVM的作用在于对筛选后的样本进行训练，得到最终的预测模型。试验结果表明，预筛选的过程可以缩短模型计算时间，同时提高最终的预测准确度，并且抽样率为0.75时取得最好的预测效果。在SVM模型训练阶段，测试了不同核函数的预测效果，结果表明linear核函数的预测效果最好。

在实际应用中，该模型可以运用于公交到站时间预测系统。下一步研究工作中，将针对预测的实时性，融合不同算法进行互补。并对输入特征进行相关性分析，筛选出有效特征，以降低预测模型的复杂度，提高公交停靠时间预测的精度和稳定性。

[1] MA X, LIU C, WEN H, et al. Understanding commuting patterns using transit smart card data[J]. Journal of Transit Geography, 2017, 58: 135-145.

[2] BIE Y, XIONG X, YAN Y, et al. Dynamic headway control for high-frequency bus line based on speed guidance and intersection signal adjustment[J]. Computer- Aided Civil and Infrastructure Engineering, 2020, 35 (1): 4-25.

[3] SZETO W Y, SOLAYAPPAN M, JIANG Y. Reliability- based transit assignment for congested stochastic transit networks[J]. Computer-Aided Civil and Infrastructure Engineering, 2011, 26 (4): 311-326.

[4] YAN Y, LIU Z, MENG Q, et al. Robust optimization model of bus transit network design with stochastic travel time[J]. Journal of Transportation Engineering, 2013, 139 (6): 625-634.

[5] RAJBHANDARI R, CHIEN S I, DANIEL J R. Estimation of bus dwell time with automatic passenger counter information[C]. Transportation Research Record: Journal of the Transportation Research Board, 2003, 1841 (1): 120-127.

[6] BIE Y M, WANG Y H, ZHANG L. Impact of carriage crowding level on bus dwell time: modelling and analysis[J]. Journal of Advanced Transportation, 2020, 2020: 1-11.

[7] BERTINI R L, EL-GENEIDY A M. Modelling transit trip time using archived bus dispatch system data[J]. Journal of Transportation Engineering-ASCE, 2004, 130 (1): 56-67.

[8] JAISWAL S, BUNKER J, FERREIRA L. Influence of platform walking on BRT station bus dwell time estimation:Australian analysis[J]. Journal of Transportation Engineering, 2010, 135 (12): 1173-1179.

[9] MENG Q, QU X B. Bus dwell time estimation at bus bays: a probabilistic approach[J]. Transportation Research Part C: Emerging Technologies, 2013, 36: 61-71.

[10] 杨敏, 丁剑, 王炜. 基于ARIMA-SVM模型的快速公交停站时间组合预测方法[J]. 东南大学学报: 自然科学版, 2016, 46 (3): 651-656.

[11] YU B, YANG Z Z, CHEN K, et al. Hybrid model for prediction of bus arrival times at next station[J]. Journal of Advanced Transportation, 2010, 44: 193-204.

[12] CAO L J, TAY F E H. Support vector machine with adaptive parameters in financial time series forecasting[J]. IEEE Transactions on Neural Networks, 2003, 14 (6): 1506-1518.

[13] VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer, 2000.

[14] YU B, WANG H, SHAN W X, et al. Prediction of bus travel Time using random forests based on near neighbors[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 33 (4): 333-350.

[15] 童小龙, 卢冬生, 张腾, 等. 基于时间序列法的公交车站间行程时间预测模型研究[J]. 交通运输工程与信息学报, 2017, 15 (4): 114-119, 126.

[16] MILKOVITS M. Modeling the factors affecting bus stop dwell time: use of automatic passenger counting, automatic fare counting, and automatic vehicle location data[C]. Transportation Research Record: Journal of the Transportation Research Board, 2008, 2072: 125-130.

[17] TIRACHINI A. Bus dwell time: the effect of different fare collection systems, bus floor level and age of passengers[J]. Transport Metrica A, 2013, 9 (1): 28-49.

Prediction of Bus Dwell Time Using Support Vector Machine Based on Near Neighbors

HUO Hao, ZHENG Chang-jiang, SHEN Jin-xing

(College of Civil and Transportation Engineering, Hohai University, Nanjing 210098, China)

To improve the accuracy of predicting bus travel times and the overall service level of a transit system, a bus dwell time prediction model is proposed in this study. Three contributing factors are considered: the number of boarding and alighting passengers, the number of passengers in a bus, and current weather conditions. A training set is selected in advance, and the effects of different selection rates and kernel functions on the prediction performance are analyzed. Ten typical stations on the No. 301 bus line in Foshan, China are chosen to test the prediction performance of the support vector machine based on near neighbors method, and the properties of each stop are analyzed. The results indicate that the proposed model achieves high accuracy, namely, an-square (2) value of 0.4255 and a root mean square error () of 9.4737. The computation time is reduced by approximately 40% as compared with the model without data preselection. The preselection process for the training data set can shorten the calculation time and reduce the prediction error. In addition, the support vector machine based on a linear kernel function performs better than those methods based on other kernel functions.

traffic engineering; prediction model; support vector machine; dwell time; urban bus

1672-4747（2021）03-0059-08

U491.1+4

A

10.19961/j.cnki.1672-4747.2020.11.001

2020-11-02

2020-12-24

2021-05-06

国家自然科学基金（51808187）；江苏自然科学基金（BK20170879）；中央高校基本科研业务费专项资金（2019B13514)；江苏省博士后科研资助计划项目（1701086B）

霍豪（1994—），男，硕士研究生，研究方向为基于大数据的公交行程时间预测，E-mail：huohaoreader@163.com

沈金星（1985—），男，博士，副教授，研究方向为基于数据驱动的多模式公交系统优化，E-mail：shenjx03@163.com

霍豪，郑长江，沈金星. 基于近邻和SVM的公交停靠时间预测[J]. 交通运输工程与信息学报，2021, 19(3): 59-66.

HUO Hao, ZHENG Chang-jiang, SHEN Jin-xing. Prediction of Bus Dwell Time Using Support Vector Machine Based on Near Neighbors [J]. Journal of Transportation Engineering and Information, 2021, 19(3): 59-66.

（责任编辑：刘娉婷）