闭环供应链中智能托盘共用的价值研究

邱小平，罗 茂，谈艳俐，刘宇辰

闭环供应链中智能托盘共用的价值研究

邱小平，罗 茂，谈艳俐，刘宇辰

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 综合交通运输智能化国家地方联合工程实验室，成都 611756；3. 综合运输四川省重点实验室，成都 611756）

随“互联网+物流”产生的智能托盘，为带板运输提供新的发展机遇，而目前对智能托盘应用价值的研究较为缺乏。本文以三级供应链中托盘共用为背景，构建智能托盘与传统托盘混合共用的闭环循环流通系统，将循环周期分为八个阶段，建立系统总成本和效益测算模型，分别以传统托盘返还率、损坏率和智能托盘损坏率为随机变量测算系统总成本与效益。测算结果表明，相较于传统托盘的在途丢失和周转效率，使用智能托盘能更有效地降低系统总成本并提升效益，传统托盘的适量损坏并不会提高系统总成本，而智能托盘的损坏与系统总成本呈正相关关系，因此智能托盘的使用将提升托盘共用系统的稳定性。

物流工程；托盘共用；成本模型；智能托盘；闭环供应链

0 引 言

作为一类典型的可回收运输载具（Returnable Transport Items, RTIs），托盘在生产、仓储和运输等环节为成件、零散的适盘货物流通提供有力的支持。在实际流通中，已证实托盘对提升流通效率和降低流通成本的作用。近年来，随“互联网+物流”诞生的智能托盘，具备优异的货物识别、定位追踪、数据传输和循环回收功能，更为托盘共用快速发展提供契机。但与普通托盘相比，智能托盘的单位制造成本和基础设施成本投入更高，使智能托盘的实际应用价值尚待商榷。

托盘共用由来已久，吴清一[1]认为托盘共用具有重大社会价值且是衡量物流现代化水平的标志。目前对托盘共用的研究主要集中在组织模式[2-4]、托盘调配[5-8]、应用策略[9-11]等方面，且均集中在研究普通托盘，未能体现智能托盘的应用价值。而对RTIs研究中，已有对载具应用对比[12, 13, 18]和闭环循环运作[14-16]的构想，对于智能托盘的价值表现，有较大的启发。

本文在参考Kim等[15]对集装箱循环流程和成本归类的研究基础上，基于共用托盘的特征，搭建了传统托盘与智能托盘两者混合的托盘共用系统及其运营成本测算模型，研究两类托盘在共用系统中对总成本和效益的影响，以此测度智能托盘的使用价值。

1 问题描述与假设条件

本文构建的是以托盘为货物载具的闭环运输系统，含有一个托盘共用资源池。这个资源池可由专业的托盘服务供应商来提供，共用的托盘会在货物供应商、运输服务者和零售商之间循环流通。一个周期内，承运方要完成供应商交付的托盘数量为的货物，由传统托盘和智能托盘共同运输。

表1 各符号代表的变量

重新进入共用托盘资源池的托盘比率记为(1-)，其中表示检修后不再共用的托盘占比，通常(1-)<1，即共用托盘资源池中的可用托盘资源小于等于需要流通托盘的数量，此时需从闭环系统外引增托盘加以补充，比如租赁或购置。当然，也存在(1-)≥1的情况，如往期滞留零售商的托盘在本期返还。此时，将安全量扣除，转化为前一种情形时，再重新进入流通循环。这两种情形的共用托盘流动如图1所示。

同时还有如下假设：

（1）共用托盘具有使用周期，包括装载、运输至零售商、延迟使用、返还至承运方、卸载、检查、维修、空盘储存等活动，主要考虑3个过程，分别对应3个时间。如图2所示，从1到4的顺序活动放在一起称为托盘在用过程，该过程所用时间称为在用时间，记为（0<<1）；从5到8的顺序活动放在一起称为托盘待用过程，其所用时间称为待用时间，记为（0<<1）；从0或8到1的过程称为托盘装载过程，其所用时间称为装载时间，记为𝛿（0<𝛿<1）。通常卸载过程较短，其时间未计入成本。

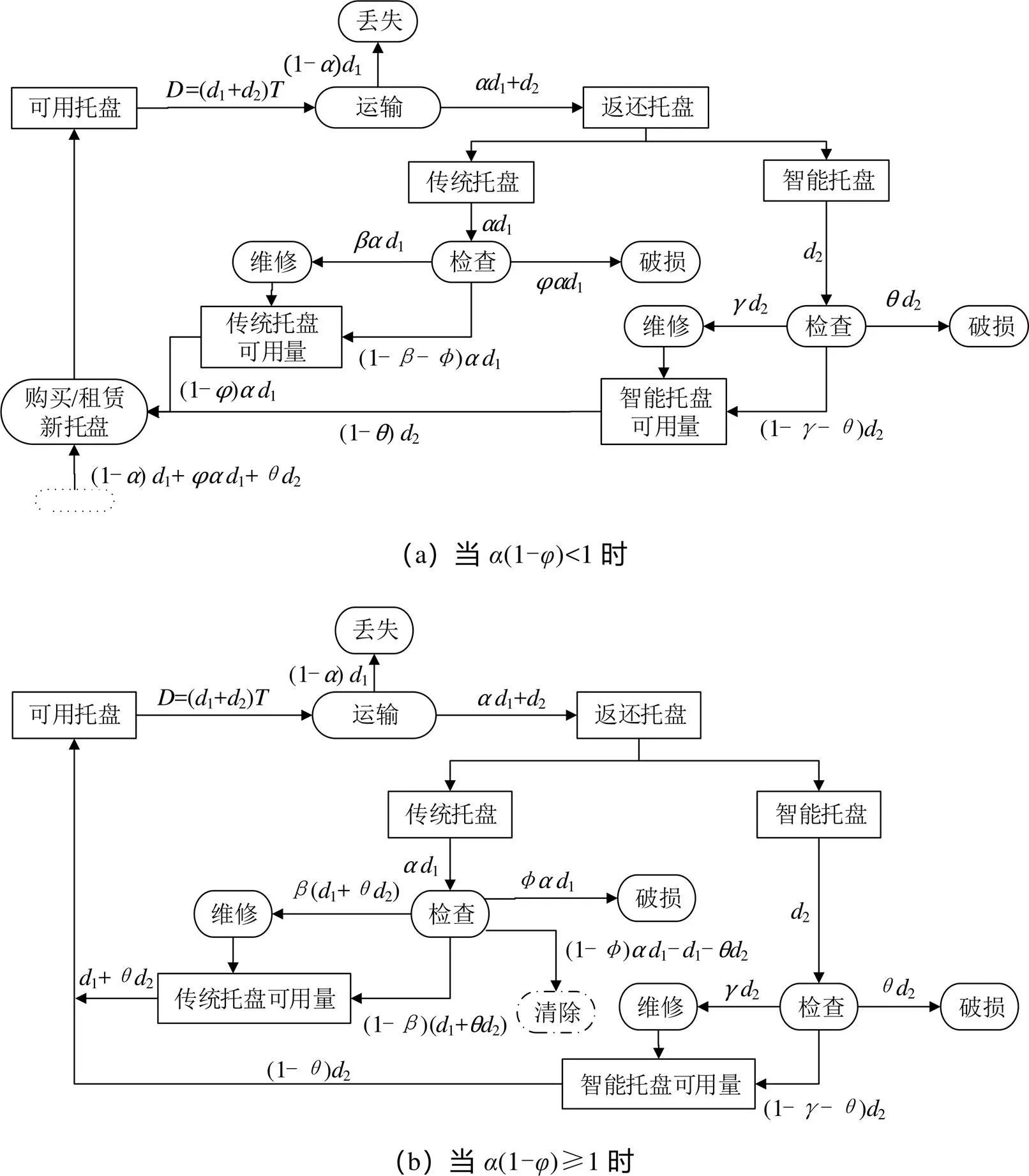
图1 共用托盘的闭环流动

0—1：装载；1—2：运输至零售商；2—3：延迟使用；3—4：返还至运输服务者；4—5：卸载；5—6：检查；6—7：维修；7—8：空盘储存；8—1：装载

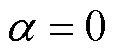
（3）在闭环运输系统中，由于传统托盘和智能托盘同时混合使用，与智能托盘有信息关联的传统托盘的丢失率也会变低。同时智能托盘的优越性可使清空货物的共享托盘及时返还回收，减少托盘延迟时间，从而获得更高的托盘流转率，有利于承运商预测并备货。

（4）由于使用智能托盘还需要配套相应的基础设施，所以闭环运输系统中还需要在固定成本中计入智能托盘的基础设施配套费用。

2 模型建立

在闭环运输系统中，基于传统托盘和智能托盘的运营成本函数可建立出系统的总成本与效益测算模型。

2.1 传统托盘的运营成本函数

由前面假设可知，传统托盘返还数量会因丢失或清除而发生变化，存在如下两种情况。

（1）当(1-)<1时

此时，需通过租赁/购置新托盘的方式来补足传统托盘的减少量。因此，传统托盘运营成本（N1）由三部分费用组成，即固定费用（N1）、可变费用（N1）和库存费用（N1），表示如下：

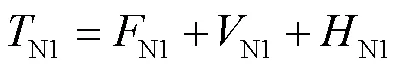
式中，固定费用由固定检查费用（IN）和订单费用（ON）计算得到，按单位时间计算：

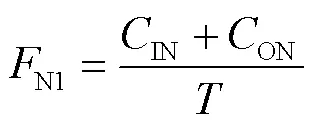
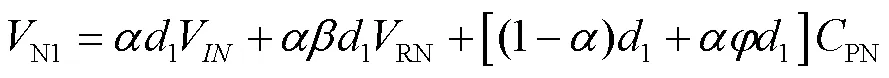
库存费用由托盘在用时的单位库存费用（u）、维修时单位库存费用（r）、空盘待用时的单位库存费用（s）与对应托盘数量的乘积之和得到，其中待用的空托盘数等于返还直接入库的托盘数、维修后入库的托盘数、租赁/购置新托盘数（包括旧托盘维修后新增的托盘数）和按需出库时的变化托盘数之和。各阶段托盘库存量的变化，如图3所示，库存费用可表示为：

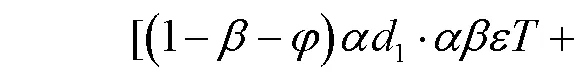
（4）

（2）当(1-)≥1时

此时传统托盘的增加量大于托盘损坏数量，没有新托盘租赁/购置。传统托盘的运营成本（N2）同样是固定费用（N2）、可变费用（N2）与库存费用（N2）的总和，即：

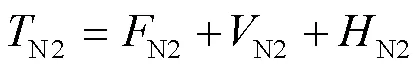
式中，固定费用（N2）的计算，不租赁/购置新托盘则不考虑对应成本项，即：

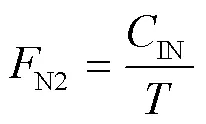
可变费用（N2）中同样去掉租赁/购置新托盘的成本项，增加需维修托盘的成本项，即：

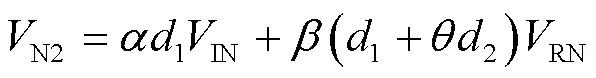
库存费用（N2）中，维修阶段、空盘待用阶段的库存量发生了变化，如图4所示，即：

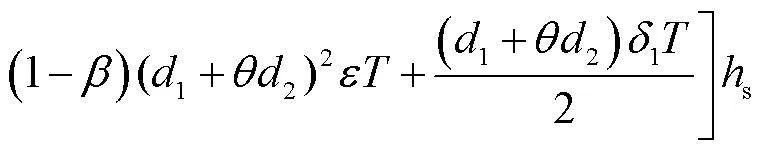
综上，传统托盘的运营总成本（N）为两种情形的运营成本之和：

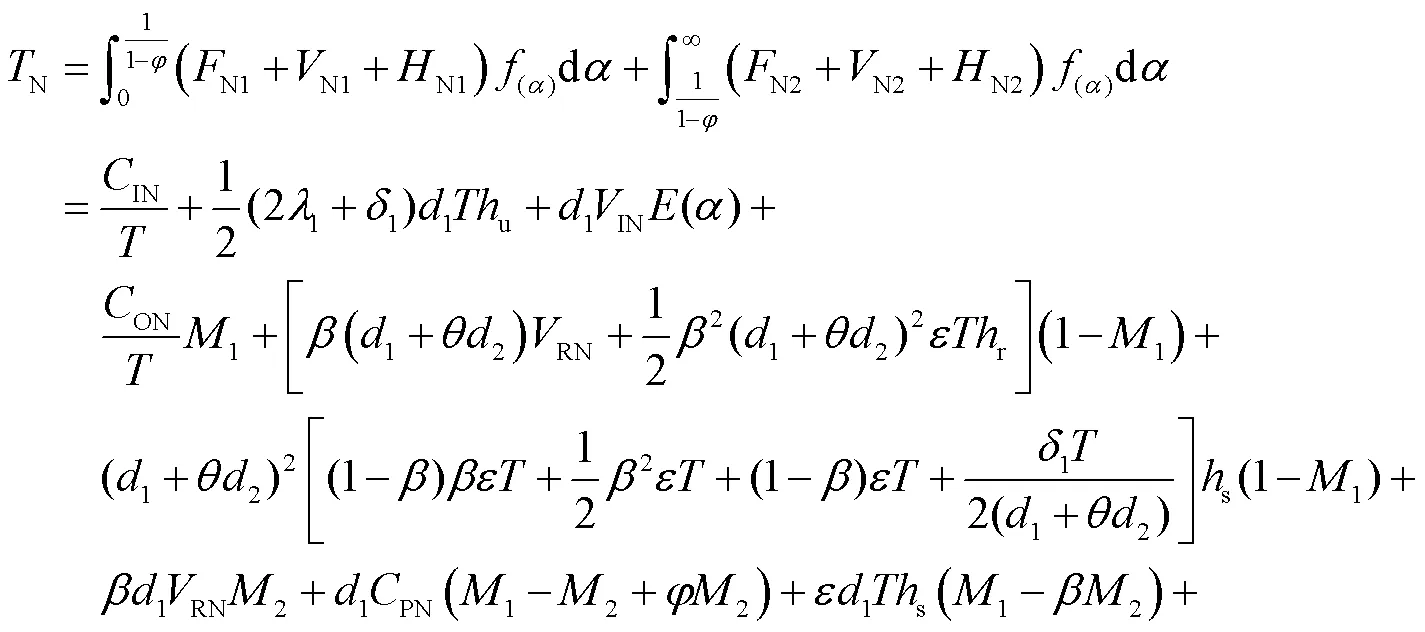
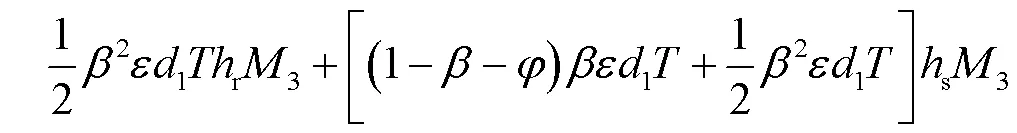
2.2 智能托盘的运营成本函数

由于忽略智能托盘的丢失，智能托盘的运营成本函数显得比传统托盘简单，如下所述。

智能托盘的运营成本（I）是固定费用（I）、可变费用（I）与库存费用（I）的总和，即：

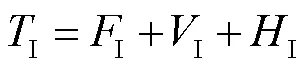
智能托盘的固定费用是托盘固定检查费用（II）、订单费用（OI）及基础设施预期费用（II）之和，即：

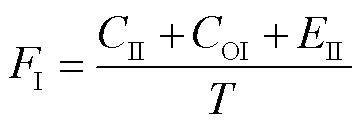
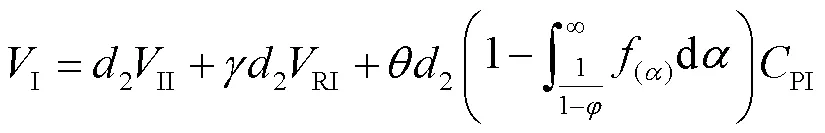
智能托盘的库存费用是托盘在用时的单位库存费用（u）、维修时的单位库存费用（r）、在库待用时的单位库存费用（s）分别与对应托盘数量的乘积之和，其中在库待用的托盘数量等于返还直接入库的托盘数、维修后入库的托盘数、租赁/购置新托盘数和按需出库时变化的托盘数之和。各阶段托盘库存量的变化如图5所示，库存费用表示为：

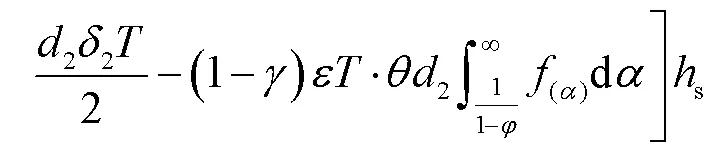
由此可得，智能托盘的运营成本函数（I）为：

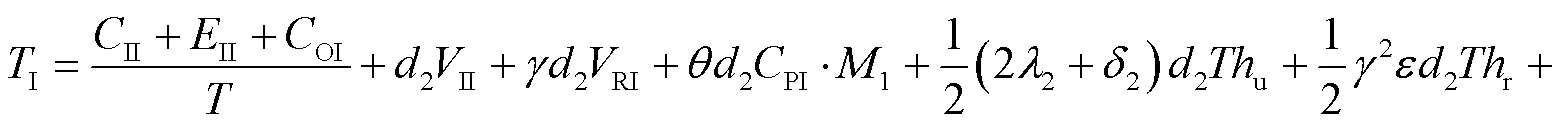
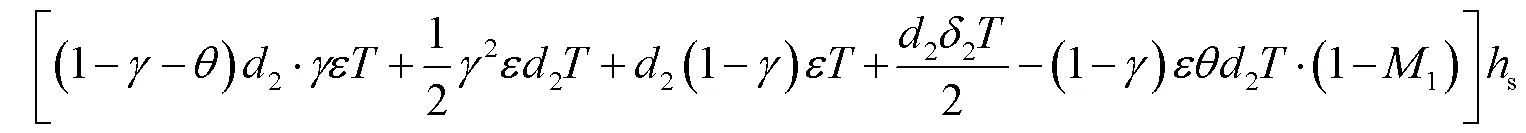
2.3 系统运营的总成本

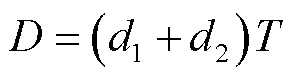
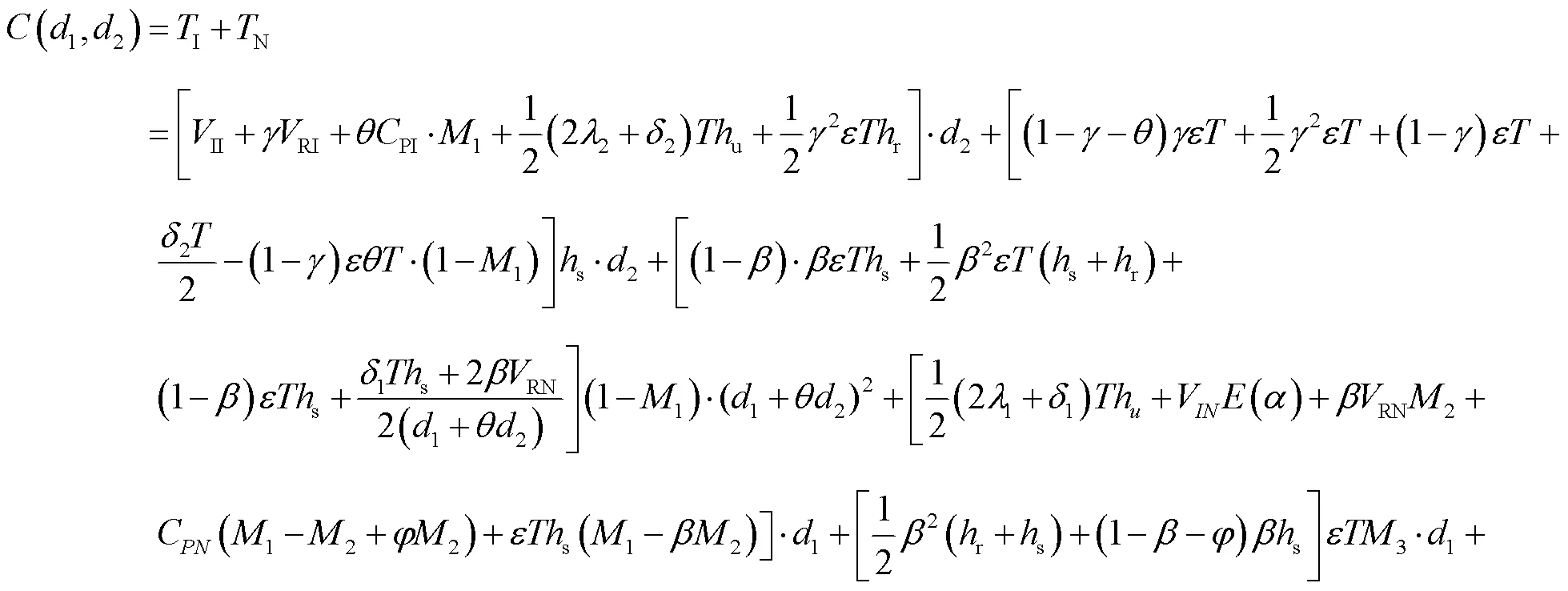
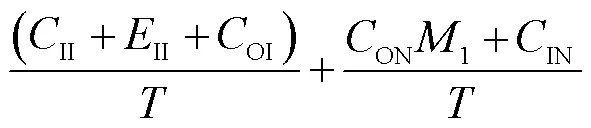
2.4 系统效益

在已知闭环运输系统运营总成本的基础上，为了探讨智能托盘的价值情况，现假设效益为，下式成立：

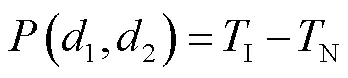
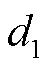
3 数值实验

基于上述参数标定，可以得到下式所示的运营总成本函数表达式：

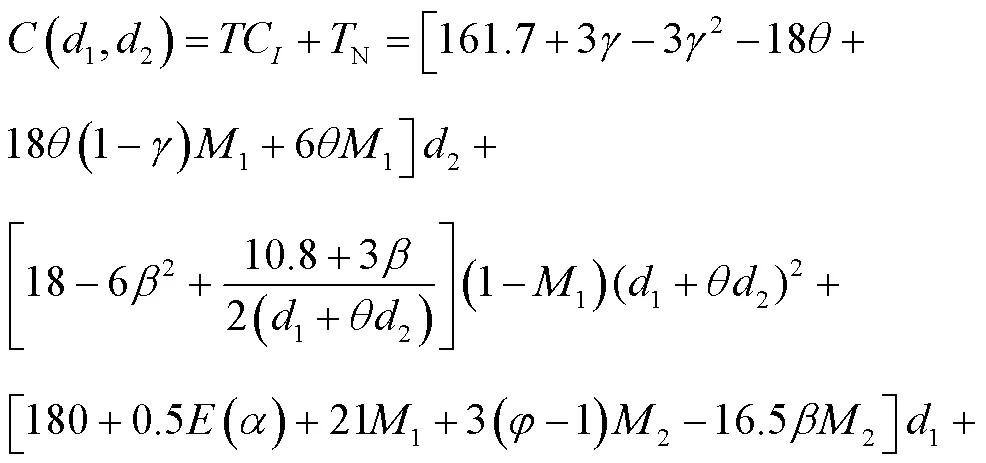
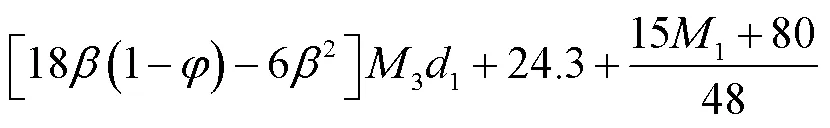
上式是关于两类托盘的需求率、返还率、维修率和破损率的二次函数，将式中第2、第3、第4、第6项的正号变换为负号，就得到效益函数。

3.1 返还率α对系统总成本的影响

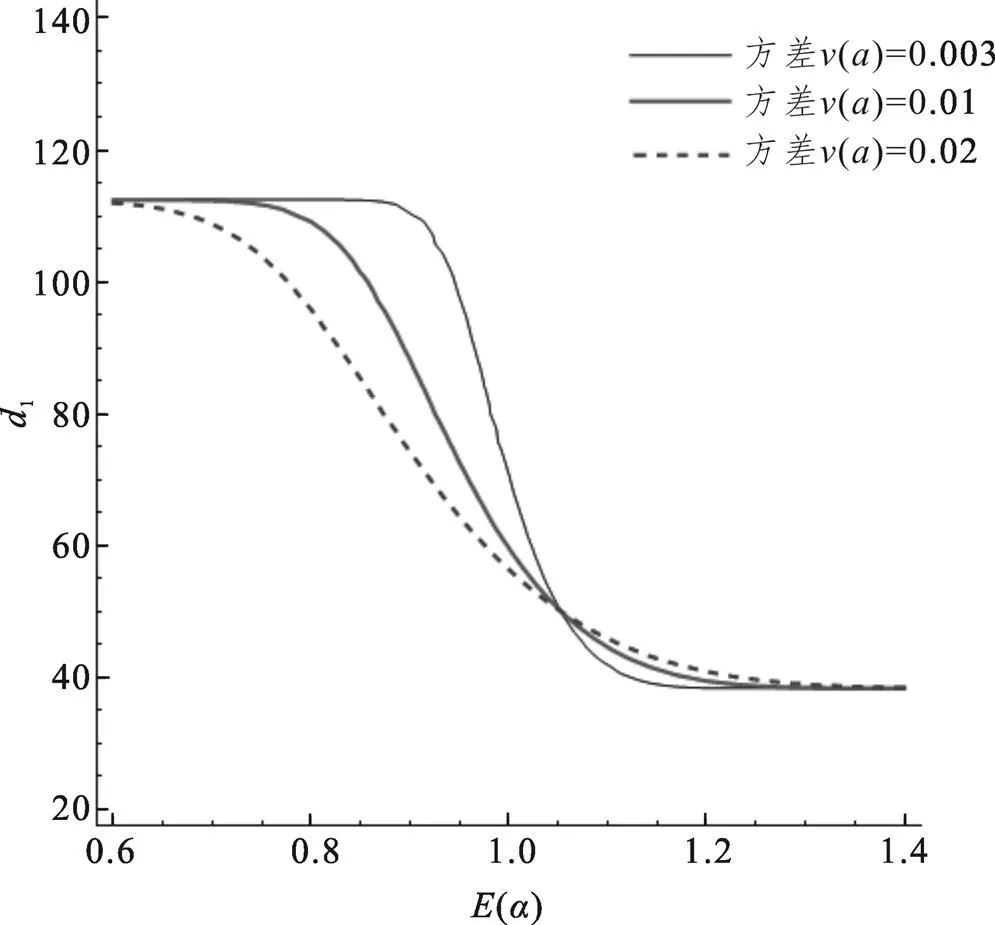
图6 传统托盘的返还率对临界值的影响趋势

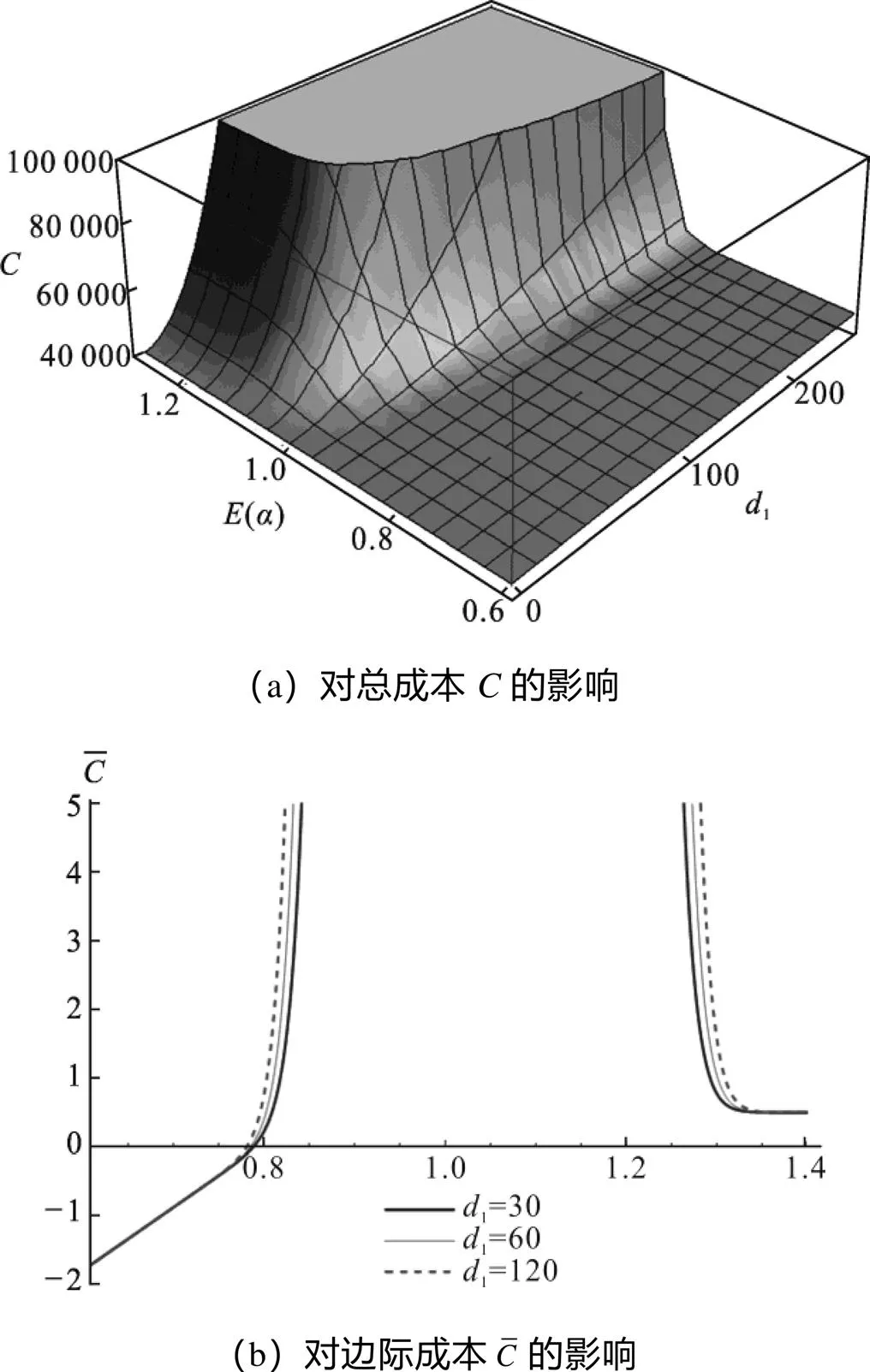
图7 服从正态分布（方差0.003）的传统托盘返还率对总成本C(a)和边际成本的影响

3.2 损坏率φ对总成本效益的影响

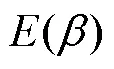
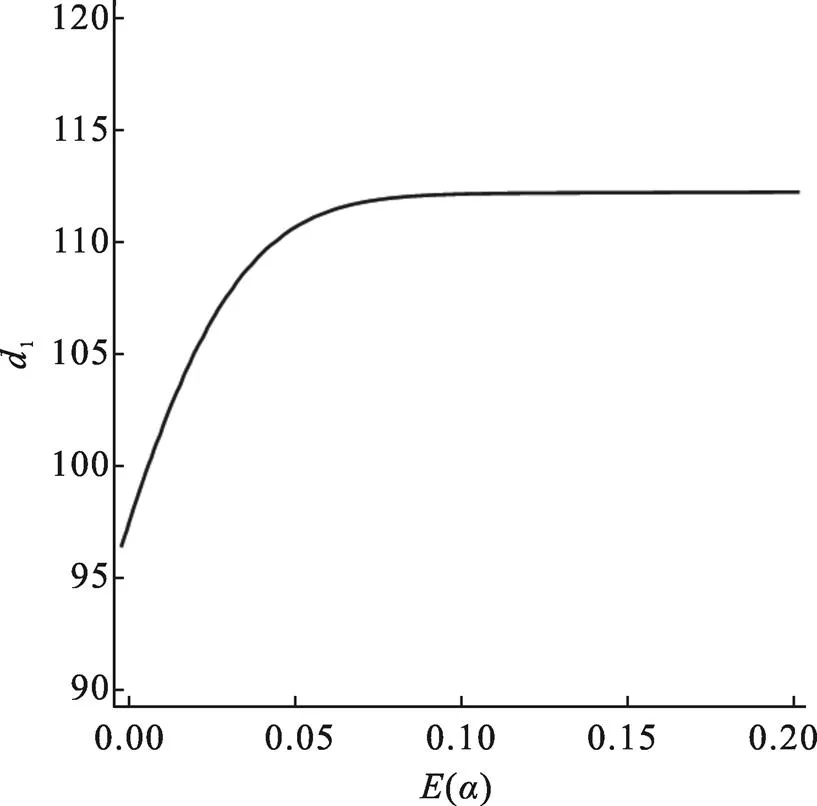
图8 损坏率φ对临界值的影响

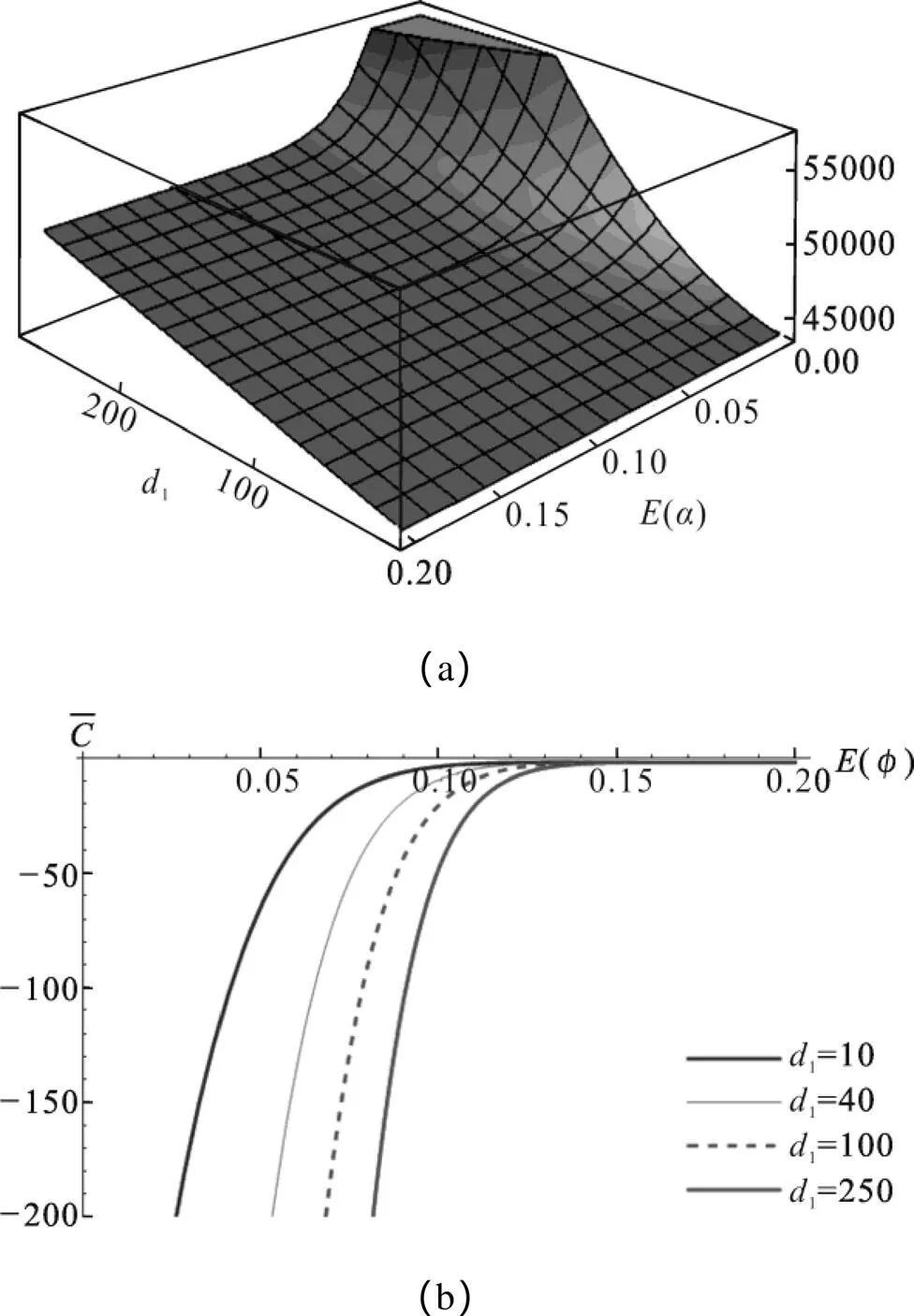
图9 损坏率φ对总成本C和边际成本的影响

3.3 损坏率θ对总成本效益的影响

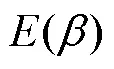
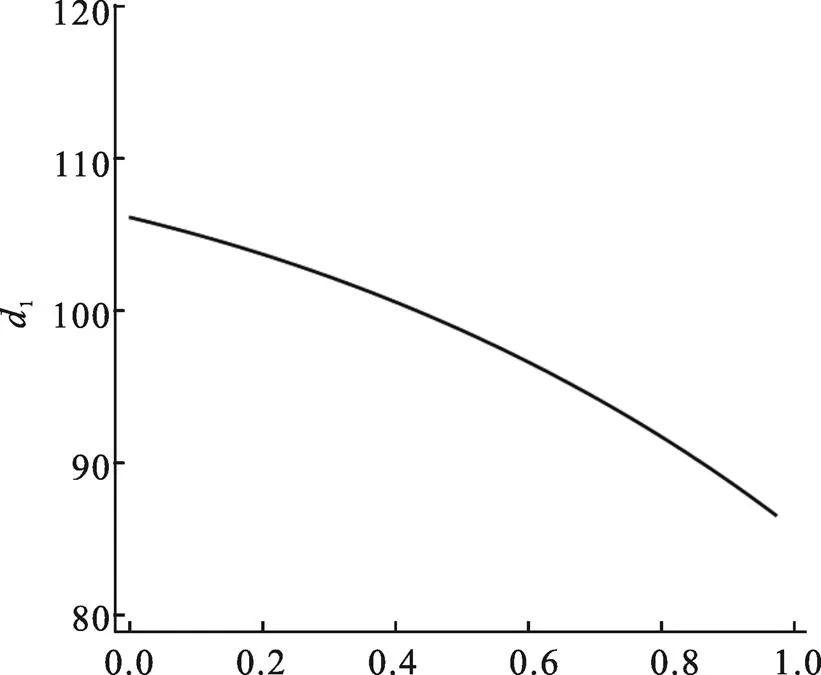
E(θ)

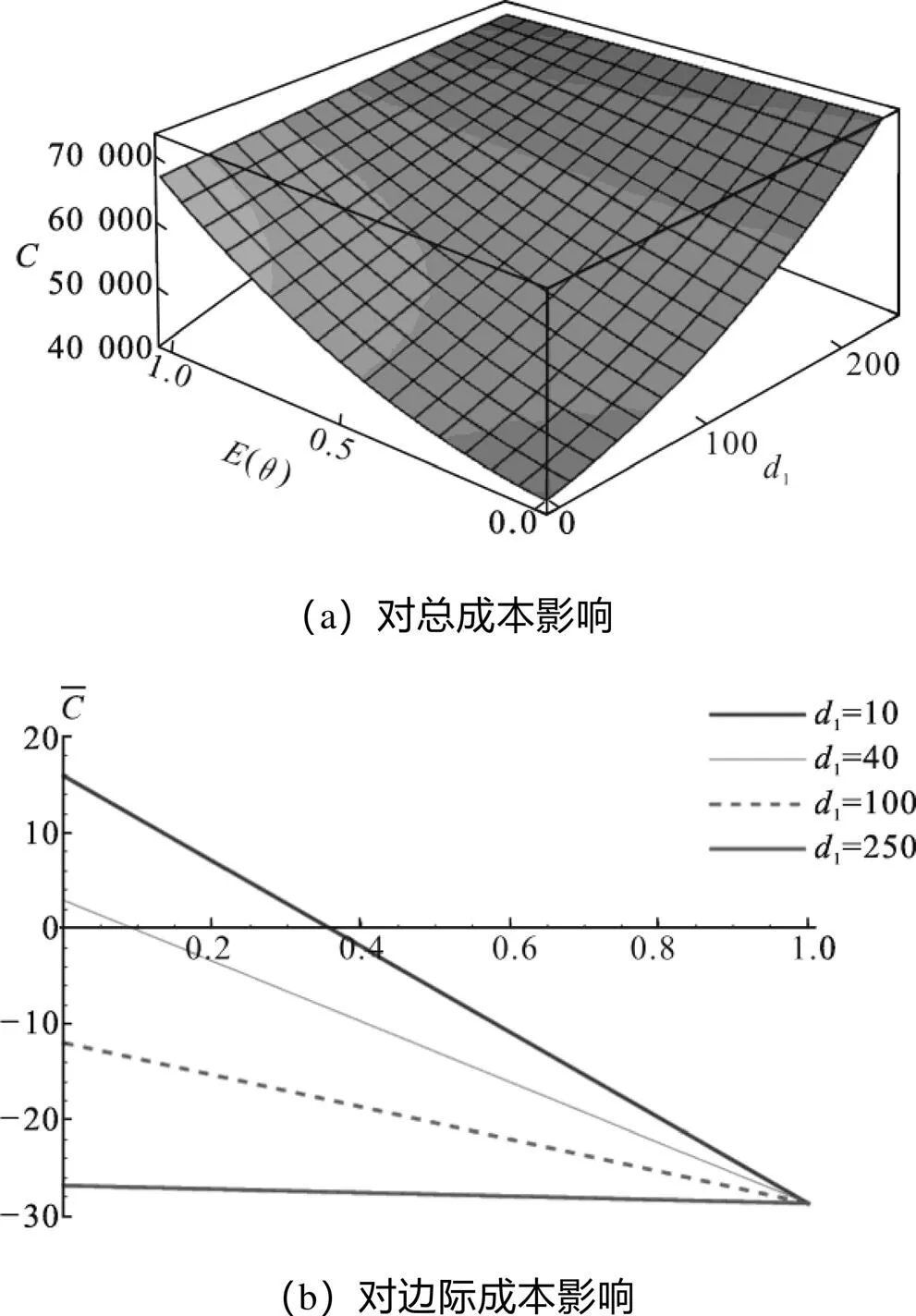
图11 损坏率θ对总成本C和边际成本的影响

4 结 论

智能托盘具有识别、定位和数据传输等功能，由于其较高的单位制造成本和基础设施成本，其实际应用尚待研究。本文在Kim等[15]研究集装箱循环流程、成本归类、定价方案和扩散周期的基础上，针对托盘体积小、易丢失和易周转的特性，侧重分析托盘共用循环流程，得到基于流程的成本测算方法，由此比较智能托盘和传统托盘的运营成本和价值表现，得到的具体结论包括：

（1）假定智能托盘的单位使用成本是传统托盘的2倍，且其基础设施成本较高，此时，智能托盘的不易丢失、周转较高的优势可带来总成本15%～20%的降低。

（2）从成本效益角度看，智能托盘较高的使用价值和周转效率，能更稳定的保障托盘共用的开展。表现为低于特定值的传统托盘丢失和损坏对总成本影响较小，超过特定值则成本波动较大，总成本随传统托盘返还率和损坏率呈连续、剧烈变化；而总成本随智能托盘损坏呈连续、平缓变化，智能托盘表现出更稳定的效益。

本文假设在闭环供应链托盘共用环境下，构建智能托盘和传统托盘混合共用的成本和效益模型，选取扰动系统总成本的主要变量展开深入分析，发现智能托盘更有利于降低共用成本和推行托盘共用。

[1] 吴清一. 论中国托盘共用系统的建立[J]. 铁道货运, 2005(9): 1-5.

[2] 周康, 何世伟, 游玲君. 基于铁路运输的托盘共用模式研究[J]. 铁道运输与经济, 2013, 35(10): 83-87.

[3] ELIA V, GNONI MG. Designing an effective closed loop system for pallet management[J]. International Journal of Production Economics, 2015, 170: 730-740.

[4] 胡悦秀, 丁静之, 丁朴. 铁路开展托盘共用业务运营模式探讨[J]. 物流工程与管理, 2018, 40(4): 45-47.

[5] WU J, REN J, LIU B, et al. Deterministic and multi-scenario models for pallet allocation over a pallet pool in a city joint distribution system[J]. Advances in Mechanical Engineering, 2016, 8(1): 1-8.

[6] 何彦东, 林云, 王旭, 等. 不确定环境下托盘调度多目标优化模型[J]. 系统工程, 2016, 34(11): 119-124.

[7] REN J, LIU B, WANG Z. An optimization model for multi-type pallet allocation over a pallet pool[J]. Advances in Mechanical Engineering, 2017, 9(5): 1-9.

[8] 王征宇, 任建伟, 马钰淇, 等. 基于城市共同配送系统的托盘共用调度随机规划模型[J]. 公路交通科技, 2018, 35(4): 146-152.

[9] ROY D, CARRANO A L, PAZOUR J A, et al. Cost-effective pallet management strategies[J]. Transportation Research Part E, 2016, 93: 358-371.

[10] CARRANO AL, PAZOUR JA, ROY D, et al. Selection of pallet management strategies based on carbon emissions impact[J]. International Journal of Production Economics, 2015, 164: 258-270.

[11] TORNESE F, PAZOUR J A, THORN B K, et al. Investigating the environmental and economic impact of loading conditions and repositioning strategies for pallet pooling providers[J]. Journal of Cleaner Production, 2018, 172: 155-168.

[12] GRIMES-CASEY H G, SEAGER TP, THEIS TL, et al. A game theory framework for cooperative management of refillable and disposable bottle lifecycles[J]. Journal of Cleaner Production, 2007, 15(17): 1618-1627.

[13] HARIGA M GLOCK C H, KIM T. Integrated product and container inventory model for a single-vendor single-buyer supply chain with owned and rented returnable transport items[J]. International Journal of Production Research, 2016, 54(7): 1964-1979.

[14] BOTTANI E, MONTANARI R, RINALDI M, et al. Modeling and multi-objective optimization of closed loop supply chains: A case study[J]. Computers & Industrial Engineering, 2015, 87: 328-342.

[15] KIM T, GLOCK CH. On the use of RFID in the management of reusable containers in closed-loop supply chains under stochastic container return quantities[J]. Transportation Research Part E, 2014, 64: 12-27.

[16] GLOCK CH, KIM T. Safety measures in the joint economic lot size model with returnable transport items[J]. International Journal of Production Economics, 2016, 181: 24-33.

[17] REN J, CHEN C, XU H, et al. An optimization model for the operations of a pallet pool with both radio-frequency identification-tagged pallets and non-tagged pallets[J]. Advances in Mechanical Engineering, 2018, 10(1): 1-13.

[18] 牟能冶, 贾程方, 康秋萍, 等. 基于蚁群算法的共享快递盒配送回收网络优化研究[J]. 交通运输工程及信息学报, 2021, 19(1): 32-42.

Value of Intelligent Pallet for Pallet Pool in Closed-loop Supply Chain

QIU Xiao-ping, LUO Mao, TAN Yan-li, LIU Yu-chen

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu 611756, China;3. Sichuan Key Laboratory of Comprehensive Transportation, Chengdu 611756, China)

Intelligent pallets, produced using “Internet+Logistics” provides a new development opportunity for palletized transport. However, the relative theoretical research on the application value of intelligent pallets has not been conducted in detail. Based on the pallet pool in a three-stage supply chain, a closed-loop recycling system mixed with intelligent pallets and traditional pallets and was established with eight phases in this paper. Furthermore, the total system cost and performance were investigated on account of the returned and broken traditional pallet, or the broken intelligent pallets in the circulation system. The experimental results show that the intelligent pallet could reduce the total system cost and promote efficiency more effectively, compared to the loss and turnover rate of the traditional pallet. In addition, the damage to the intelligent pallet positively correlated with the total system cost, whereas the moderate damage to the traditional pallet did not increase it. Consequently, the stability of the pallet pool system was improved by applying the intelligent pallet.

logistics engineering; pallet pool; cost model; intelligent pallet; closed-loop supply chain

1672-4747（2021）03-0031-11

U294.3；F760.3

A

10.19961/j.cnki.1672-4747.2019.01.005

2020-01-04

2020-03-05

2021-07-27

国家自然科学基金（61673320）；国家重点研发课题（2019YFB2101802）；教育部人文社会科学规划基金（19Y5A630057）；成都市国际科技合作项目（2020-GH02-00064-HZ）；软科学研究项目（2020-RK00-00370-ZF）；内江市科技孵化和成果转化专项资金项目（基于区块链和运力整合的区域物流协同系统研发与示范应用）

邱小平（1976—），男，教授，博导，研究方向为物流规划与管理，E-mail：qxp@swjtu.cn

邱小平，罗茂，谈艳俐，等. 闭环供应链中智能托盘共用的价值研究[J]. 交通运输工程与信息学报，2021, 19(3): 31-41.

QIU Xiao-ping, LUO Mao, TAN Yan-li, et al. Value of Intelligent Pallet for Pallet Pool in Closed-loop Supply Chain [J]. Journal of Transportation Engineering and Information, 2021, 19(3): 31-41.

（责任编辑：刘娉婷）