基于动网格的调节阀空化流场数值模拟研究

张希恒 王 宇 张孙力

（兰州理工大学石油化工学院）

调节阀作为工业仪表的重要组成部分，在各个领域得到了广泛应用。 空化是一种当流体通过阀节流时，从缩流截面的静压降低到不大于流体在阀入口温度下的饱和蒸汽压时，部分液体汽化形成气泡，气泡溃裂恢复为液相的现象［1］。调节阀在调节流量过程中，气泡常在阀芯周围的近壁面溃裂，造成阀芯的剥蚀和振动，严重时会导致阀门调节失效。 因此，针对调节阀空化现象的研究具有重要意义。 张含等对高加疏水阀空化流场进行了数值模拟，利用多级节流降压理论优化了结构，达到了抑制空化的目的［2］。李贝贝等通过数值模拟方法对节流阀不同开度的油液空化流场进行了研究［3］。 王世鹏等通过对复合式调节阀空化现象的研究，发现提高背压可有效抑制空化现象［4］。 Jin Z J等通过对阀体进出口部件的弯曲半径、偏离距离和圆弧曲率参数的研究，发现空化强度随弯曲半径、偏离距离和进出口零件相关的圆弧曲率的增加而降低［5］。 彭龑等对调节阀内部进行了优化，使得阻力变小，急剧压差变化减弱，流量系数Kv总体增大，水力损失减小，在高压差下结构的抗空化性能更好［6］。 张斌等利用CFD动网格技术对双作用叶片泵流场动态特性进行了分析，仿真结果符合实际情况［7］。

目前，对阀门空化现象的研究主要集中在稳态流场空化规律和优化设计方面，而对于调节阀动态空化过程还需进一步研究。 笔者以单座调节阀为研究对象， 利用用户自定义函数（User-Defined Function，UDF） 对阀瓣的运动进行约束，通过CFD对其内部流体的动态特性和空化现象进行研究，为调节阀连续关阀过程的空化特性与结构优化提供参考。

1 研究对象

笔者以某DN50mm单座调节阀为研究对象，采用Solidworks软件建立三维模型，为使模拟具有更好的收敛性，对模型进行简化处理。 阀门两端出口采用加长管道，以使模拟结果更加接近真实情况，再利用DM模块抽取内部流道区域，得到调节阀简化模型与内部流道如图1所示。

图1 调节阀简化模型与内部流道

用Fluent前处理软件ICEM CFD、结合混合网格划分技术对流体域进行网格划分［8］，并根据流动特点对流道阀口位置和阀芯周围空化区域进行加密，如图2所示。 通过网格无关性验证和步长独立性验证，选用网格数量为937 414的模型进行模拟计算。

图2 调节阀流道网格划分

2 计算模型

2.1 空化模型

通过对比分析Kunz空化模型、Zwart-Gerber-Belamri空 化 模 型 和Schnerr-Sauer空 化 模 型［4］，发现Schnerr-Sauer空化模型可以较好地体现湍流脉动压力对气化压力的影响［9］，因此笔者选用Schnerr-Sauer空化模型建立控制方程。

当pv≥p时：

式中 p——某温度下的绝对压力；

pv——饱和蒸汽压；

RB——空泡半径；

Rc——凝结相生成率；

Re——蒸发相生成率；

αv——蒸汽相体积分数；

ρ——混合相密度；

ρl——液体密度；

ρv——气体密度。

2.2 动网格计算模型

对于通量φ，在任一控制体V内，其边界是运动的，则守恒方程的通式［10］为：

∂V——控制体V的边界；

Γ——扩散系数。

2.3 参数设置

模拟计算设置工作流体为水和水蒸气，物性参数见表1。 选用Mixture计算模型模拟气液两相流动；湍流模型选用Realizable k-ε湍流模型［9］；近壁面采用标准壁面函数。

表1 工作流体物性参数

在管道两端设置压力边界， 进口压力为2.2MPa，出口压力为0.8MPa。 首先进行稳态计算，再以稳态收敛的计算结果为初值进行瞬态计算。关阀时间设置为0.500s，时间步长6.25×10-5s，通过UDF来驱动阀芯以50mm/s的速度关闭阀门。

3 计算结果与分析

3.1 压力场与速度场

图3、4为不同关阀时刻的压力和速度矢量分布云图。 从图3、4可以看出，流体以较高的速度通过阀芯边缘与阀口内壁之间的间隙，表现为射流现象。 射流在阀口下游形成一对旋向相反、大小近似相等的漩涡，且在阀口处和阀口下游流道中心形成高流速区域，高流速区域的大小和最大流速均随着阀芯的下降呈先增大后减小的趋势。 在阀全开时，由于射流的影响，阀口下游靠近阀体壁面处形成漩涡A，造成部分流体回流，带来负压区域a。 在t=0.100s时，阀口下游的射流速度减小，漩涡A强度减小，压力升高，负压区域a消失。 阀芯边缘与阀口内壁之间的间隙流速增大，最大流速为59.42m/s。 由于间隙两侧漩涡的影响，在阀口处形成了新的负压区域b。 在t=0.200s时，阀芯边缘与阀口内壁之间的间隙流速达到最大， 其值为62.30m/s。 间隙内负压区域b进一步扩大。 t在0.200～0.500s时，通流截面积减小，在液体粘性阻力的共同作用下使得最大流速降低，高流速区域减小且主要集中在阀芯边缘与阀口内壁之间的间隙内，间隙两侧形成的漩涡强度以及间隙内的负压区均呈先增大后减小的趋势，导致该处流体 流速变化快，形成负压区，易产生空化噪声。

图3 不同关阀时刻压力分布云图

图4 不同关阀时刻速度矢量分布云图

3.2 空化区域

图5为不同关阀时刻的气相体积云图。 从图5可以看出，在阀全开时，阀座下游A处发生空化，且A处空化程度相对较强；随着阀芯的下降，在t=0.100s时，阀座下游空化区域A消失，在阀座入口区域紧贴阀座表面出现新的空化区域B， 且空化区域的气相体积减小， 此时空化程度弱于阀门全开时。 t在0.200～0.475s时，空化区域B进一步扩大， 呈对称分布且在阀座入口两侧及阀芯边缘与阀口内壁之间的间隙内，随着开度的减小，空化区域的气相体积逐渐增加， 空化程度达到最大。

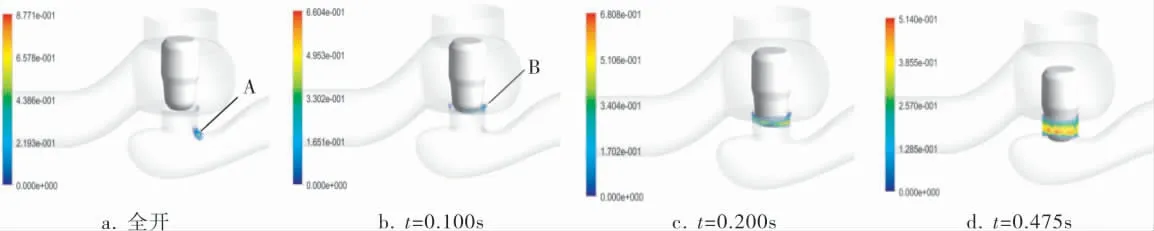
图5 不同关阀时刻气相体积云图

3.3 动态与稳态空化结果对比

不同阀芯关闭速度下含气率与开度的关系曲线如图6所示。 从图6可以看出，当阀芯以一定的速度关闭时， 随着阀芯的下降 （开度的减小）， 阀内的含气率总体上呈先增大后减小的趋势。 对比稳态空化模拟， 两者在相同的关阀速度下开度与阀内含气率的变化趋势基本一致。

图6 不同阀芯关闭速度下含气率与开度的关系曲线

图7为不同阀芯关闭速度下阀芯轴向力与开度的关系曲线。 从图7可以看出，阀芯关闭速度对阀芯轴向力的影响较小。 当开度大于21mm时，阀芯轴向力与开度成线性关系； 当开度小于21mm时，由于介质空化作用使得阀芯受力不均，轴向力出现非线性波动。 对比稳态空化模拟，两者在相同的关闭速度下开度与阀芯轴向力的变化趋势基本一致。

图7 不同阀芯关闭速度下阀芯轴向力与开度的关系曲线

4 结论

4.1 关阀时阀芯边缘与阀口内壁之间的间隙易发生空化。 此处空化易破坏阀芯，造成阀门调节功能失效，从而危害工业的安全生产。

4.2 随着阀开度减小， 通过阀口处的流体速度、阀芯边缘与阀口内壁之间的负压区以及阀内的含气率都呈先增大后减小的趋势。

4.3 不同关阀速度下含气率和阀芯轴向力随开度的变化趋势基本一致，表明在一定范围内关阀速度对阀门空化基本无影响。

4.4 对比动态和稳态空化过程，在相同关阀速度下含气率和阀芯轴向力随开度的变化趋势一致，表明利用动网格模拟关阀的动态过程具有可行性。 该模拟方法可为研究其他运动流场空化特性提供一定的参考。