彭罗斯:当代的达·芬奇
李新洲 奚萍
凡夫俗子常常发问,数学家与物理学家谁更伟大?答案是众说纷纭,不一而足。人们通常用是否获得诺贝尔奖来衡量一位科学家的成就,遗憾的是,诺贝尔奖并没有设立数学奖。不过,倘若你的数学与彭罗斯一样好的话,就可以拿两次诺贝尔奖,一次帮别人拿,另一次自己拿。
贴 砖 玩 家
非周期贴砖是指没有平移对称性的贴砖。彭罗斯很早就发现,用五边形、五角星形、菱形和船形4种形状的地砖组合,就可以实现非周期性平铺。1974年,彭罗斯发现用两种菱形地砖就可以等价地实现这种非周期性的平铺,现在这种地砖被命名为彭罗斯地砖。2013年,牛津大学数学系大楼门口,已用彭罗斯地砖铺设,作为一种对彭罗斯数学造诣的崇高敬意。
1982年,谢赫特曼(Daniel Schechtman)发现钬镁锌合金中存在五边形结构,它和彭罗斯地砖一样,没有平移不变性,却有旋转2π/5不变性。当时在学术界发生了重大争议,这是一种特殊的晶体结构,还是发生了实验错误呢?后来发现,如果原子按照彭罗斯地砖那样排列,理论计算出来的X射线衍射图样就与实验完全一致。于是,准晶体被发现了,谢赫特曼获得了2011年度的诺贝尔化学奖。
彭罗斯还有很多诸如贴砖这样看似游戏的工作。譬如想象物理上不可能实现的事物的能力,是人类意识的一个奇妙特性。利用这种想象,人们可以产生意识上的共鸣、观念上的激发。1961年,彭罗斯和他的父亲(Lionel Penrose)一起构思了一种永无止境的楼梯,这就是著名的彭罗斯三角形。多才多艺的彭罗斯是我们时代的达·芬奇,彭罗斯的贡献实在太多了。以彭罗斯命名的创新实在太多了,彭罗斯定理、彭罗斯猜想、彭罗斯广义逆矩阵、彭罗斯图、彭罗斯方程、彭罗斯旗、彭罗斯扭量……不胜枚举。下面先从奇点定理说起吧!

奇 点 定 理
彭罗斯是一位数学家,原先的专长是代数几何学。在1950年代,他受到了剑桥大学的邦迪(Hermann Bondi)和夏马(Dennis Sciama)的影响,激起了他对广义相对论的兴趣。正是他的纯数学背景,他研究的方法与他人迥然不同。
直到1960年代,广义相对论的研究方法只是局域技术:爱因斯坦场方程描绘了某个事件处,物质的能动张量如何确定几何,而几何又告知物质如何运动。换句话说,这是一种局域的物理学,通过时间上的局域积分得到爱因斯坦场方程的解。非引力的物理定律,可以在时空的各个事件处的局域洛伦兹参考系中,利用等效原理得出。然而,从1963年以来,彭罗斯及其合作者对黑洞和奇性的研究,揭示出的整体性质和整体定律,简洁而优美,能与爱因斯坦的等效原理媲美。霍金指出,“彭罗斯首先发现不必去解方程,就能发现普遍规律”。
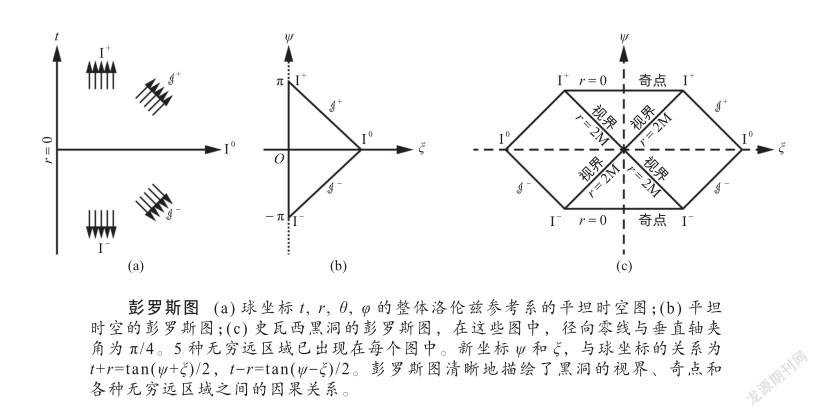
在渐近平坦时空中进行计算时,需要考虑在无穷远处物理场的渐近形式。倘若要知道超新星爆发时,引力波和电磁波会带走多少能量的问题,仅仅考虑空间无穷远的渐近形式是不够的,还必须考虑“未来无穷远”处度規的渐近形式。1964年,彭罗斯利用“共形变换”技术,将“无穷远”变到了有限半径处,渐近计算变成了有限处的计算。彭罗斯将渐近平坦时空中的“无穷远”分成了5类:


引力坍缩的终点是什么?球对称坍缩的终点是奇点,那么不对称坍缩是否可以避免奇点呢?爱因斯坦认为不对称性可以避免奇点,从而他不相信存在黑洞。但是,彭罗斯、霍金和杰罗奇(R. P. Geroch)证明了奇点定理。不论对称与否,奇点是一种非常普遍的现象,宇宙中必定存在着黑洞。1965年,彭罗斯给出了捕获面的概念,捕获面不再限定于2维球面,而是具有捕获光线的任意闭曲面。1968年,杰罗奇将奇点定义精确化,时空流形不能扩展到奇点之外。1969年,霍金和彭罗斯发表了他们的奇点定理:在广义相对论的框架内,如果时空还满足4个自然的物理条件,那么时空必定含有奇点。
战 旗 猎 猎
霍金说,彭罗斯在广义相对论中引入了旋量和整体技术的现代概念。旋量在相对论中的应用,首先产生于对空间转动的分析,接着是对时空转动的分析。考虑一个立方体,将它绕一个轴转动π/2,再绕另一个轴转动π/2。于是,立方体就从“初”指向转到了“终”指向。转动组合的规律是什么呢?倘若用矢量描述旋量,显然是错误的。因为使用矢量合成法则,得到的结果是:合成的矢量在两个矢量组成的平面上;合成矢量的大小为π/。然而,将立方体从初指向转到终指向的单一转动是:转轴从立方体中心指向一个顶角;转动的角度为2π/3。

这就是今天称为自旋矩阵的数学客体,用来描述旋量的变化。
作为一种几何客体,矢量可以形象地画成一个箭头。旋量也是一种几何客体,如何才能形象化地表示旋量呢? 这似乎太难了,超越了常人的想象力,但是彭罗斯做到了这一点。如果在地球上某处O,向月球的阿里斯塔克斯环形山的中心P发射光脉冲,并设计激光产生的不是一个光斑,而是一个箭头。彭罗斯将零矢量O P称为旗杆,亮箭头称为旗。于是,旋量就由下述几何量的三位一体构成:零旗杆、旗、旗与周围事物之间的指向—缠绕关系。通过重复发射激光脉冲,并在两次发射之间“旋转”旗,当旗旋转2π回到原来方向时,旋量反号。旗绕旗杆4nπ时,旋量恢复到原来的值。
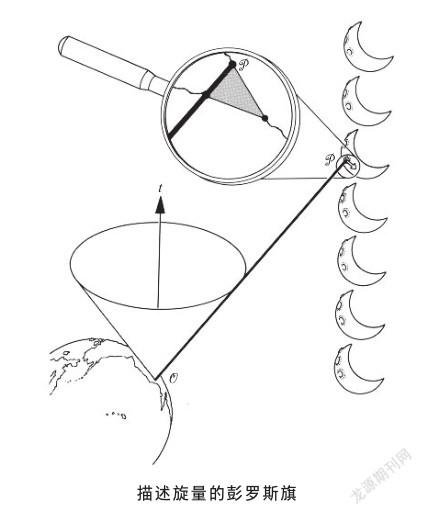
当人们研究引力对费米子的影响时,弯曲时空中的旋量分析是须臾不可离开的数学工具。引力场中费米子束缚态的分析,需要求解史瓦西时空的狄拉克方程,也就必须用到处理弯曲时空旋量的纽曼—彭罗斯方程。三位一体的旋量旗在形象地描绘更复杂的几何客体扭量时,起到了重要的作用。
扭 量 之 父
量子论的基本方程是复形式的微分方程,彭罗斯认为时空结构的基础也应当是复的。学过复分析的人,一定知道包括无穷远点的整个复平面,可以用黎曼球面表述。为了建立复的时空结构,彭罗斯将旋量发展成扭量概念,他创建了扭量理论。
位于时空某处的一位观测者,观测一颗恒星,他在天球上画出了恒星的方位角。倘若第二位观测者在相同时刻穿过同一点,如果两人之间有一个相对速度,那么由于光行差,第二位观测者会将这颗星画在不同的方位上。黎曼球面上的不同点,可以用麦比乌斯变换联系起来。通过时空点的光线空间,自然构成了一个黎曼球面。联系不同速度观测者物理的正洛伦兹群,可以用黎曼球面的自同构群实现。
彭罗斯将光线看成比时空点更为基本的客体,并将这种概念推广到整个时空。于是,扭量空间(光线空间)是比时空更为基本的空间,时空成了一个从属的概念。时空中的光线是扭量空间的一个点,而时空点则用光线的集合来表示。或者说,时空点在扭量空间中变成了一个黎曼球面。
这样的扭量空间是实5维的,而复空间必须是实偶数维的。彭罗斯认为还必须考虑到光子的能量和螺旋度,于是采用了3维复投影空间CP3,这就是投影扭量空间(PT)。它的5维子空间是PN,而PN将PT分成了左手螺旋度和右手螺旋度的两个部分PT-和PT+。

时空点用4个实数描述,而投影扭量空间的点,是用4个复数比Zα给出的。利用两个复旋量ω和π,彭罗斯表述了扭量。利用彭罗斯旗,可以形象地画出扭量的几何图形。如果将定义在PN上的扭量函数延拓到PT+,它就具有正频;延拓到PT-,便具有负频。这正是推广量子化场所需要的概念,正频部分沿时间前进方向传播,负频部分沿时间后退方向传播。正频部分也就是正能量部分构成的传播子,这样就允许人们在扭量空间中开展量子物理研究。沿着这条道路,物理学家们进一步发展出扭量图,这是类似于时空费曼图的描写相互作用的方案。
扭量理论是共形不变的,所以对于共形平坦的弯曲时空,同样可以建立扭量空间。彭罗斯不仅研究了弯曲时空的扭量理论,还进一步研究了扭量宇宙学。扭量空间是复4维的,彭罗斯对存在额外维数的10维超弦理论极不满意,彭罗斯是一位超弦理论的主要批评者。2003年,在一次与威滕(Edward Witten)的邂逅中,彭罗斯曾担心两人会发生激烈争论,想不到的是,这位弦论大师告诉他,正在研究扭量与弦论如何相结合的理论。
量 子 测 量
玻尔、海森伯和泡利在哥本哈根1927年的会议上,提出了量子力學的标准诠释。它包括不确定原理、波粒二象性、概率解释、本征值认同测量值。1932年,冯·诺依曼为哥本哈根诠释添加了最后要素:波函数坍缩。但是,爱因斯坦、薛定谔和德布罗意等物理学家并未接受这种诠释,波函数从叠加态坍缩到本征态是瞬时完成的,并没有任何物理机制。
维格纳(Eugene Wigner)是哥本哈根诠释的支持者。他设计了一个被人称作维格纳之友的理想实验。他请一位朋友去核实一个粒子物理实验结果,它在前一天已被记录。这位朋友及时将结果报告给了维格纳。于是产生了这样的问题,这个粒子事件是用波函数描述的,那么波函数是在何时坍缩的呢?倘若维格纳认为坍缩发生在向他报告时刻,那么他成了一个十足的唯我论者。他当然不会这样可笑。难道是他朋友的意识使得波函数坍缩?人类有什么异禀之处,让我们有别于物理世界的其余部分,服从不同的定律?在人类出现之前,世界一直处在不确定的叠加态中吗?坍缩是一种离散过程,意识是一种连续过程,波函数坍缩真能与连续的意识相关?
哥本哈根的波函数坍缩是一种瞬时效应,不存在任何动力学机制,引起了爱因斯坦为代表的众多物理学家的不满。彭罗斯的解决方案是力学的,他将坍缩与一个适当程度的复杂性联系起来,复杂度可用粒子数或者总质量描述。他的方案要求在薛定谔方程中,增加一个新的项,仅当达到一定条件时,附加项才起作用。彭罗斯建议,一旦卷入波函数的粒子总质量接近普朗克质量时,波函数就会自发坍缩。普朗克质量大约是10-5克,对于原子尺度,这很大;对于人的尺度,却又很小。
共 形 循 环
彭罗斯是一位共形大师,彭罗斯图、扭量都是基于共形变换的。更重要的是,他提出了共形循环宇宙学(CCC),从大爆炸开始的宇宙终于一个加速膨胀的时空,形成一个世代;每个世代的终结又是下一个世代的大爆炸开始。CCC描绘了一个无限的宇宙循环。我们宇宙的大爆炸是前一个世纪的遥远未来的延续。CCC认为我们的宇宙不会永远膨胀,更不会发生大撕裂,它会在未来某一天停止膨胀,重新回到坍缩。

作为初始奇点的大爆炸,与终端奇点的黑洞,两者都可以用共形不变的外尔曲率张量来描述,从而外尔张量成为描述引力熵的几何量。大爆炸的共形扩张将无限大的密度和温度降到有限值,而共形收缩又会将无限低的密度和温度提高到有限值。于是,两者在光滑边界上过渡,宇宙就从前一个世代进入到现今的世代。
宇宙在循环,彭罗斯的证据是宇宙微波背景辐射中存在霍金点。彭罗斯和他的合作者利用普朗克卫星的观测结果,找到了大约30个霍金点。彭罗斯等人指出,根据CCC,这些点携带了上一个世代宇宙坍缩时,黑洞蒸发后留下的遗迹。由此证明我们所在的世代之前,已经存在过另一个世代。
战 斗 友 情
彭罗斯比霍金年长11岁,曾担任霍金博士答辩的评委。霍金从彭罗斯那里学到了整体技术,用它证明了黑洞力学的第二定律,在黑洞过程中,涉及的所有黑洞表面积不会减小。他们俩还一起证明了奇点定理。霍金曾说过:“正是彭罗斯的第一条奇性定理,引导我去研究因果性结构,激发出我对奇点和黑洞经典研究的灵感。”
不过,霍金和彭罗斯的物理学观点,并非完全一致。1994年,两人在牛顿数学研究所进行了一场大辩论。在某种意义上说,这是当年玻尔和爱因斯坦辩论的继续。尽管辩论内容变得更深入复杂,但是论证无法与哲学观点分开。霍金说,彭罗斯是柏拉图主义者,他自己是实证主义者。霍金所关心的仅仅是理论预言能否与测量结果一致,而彭罗斯担忧的是既死又活的薛定谔猫的合理性。彭罗斯说,不论“实在”是什么,人们必须解释自己是如何感知世界的,人们必须解决为何感觉到的猫非死即活,不会是既死又活的叠加态猫。彭罗斯还对霍金在广义相对论中使用“维克转动”不满,认为这与量子场论中时间轴从实轴转动到虚轴是两回事。科学史上的合作与争论原本是司空见惯寻常事。但是,像根泽尔和盖茨这样的欢喜冤家并不多见,他们激烈争论,却以同一个课题获得诺贝尔奖确实罕见。1952年出生的根泽尔,长期以来利用欧洲南方天文台的望远镜观测银河系中心附近的恒星轨道运动。根泽尔团队首先发现牛顿力学无法解释这些轨道,必须要使用广义相对论才行。也就是说,轨道发生了史瓦西进动,从而推出了黑洞的存在性。
与根泽尔相比,盖茨是一位年青一代的女天文学家,从1995年开始,盖茨开始投入到黑洞研究,运用新技术手段是她成功的关键。盖茨团队开发了凯克天文台望远镜的自适应光学系统(AO系统),在2005年首先拍摄到第一张激光引导AO银河系中心照片,使得清晰度极大提高。两个团队对所观测到的现象,常常会发生针锋相对的争论。用盖茨的话来说,“没有什么比竞赛更能让人进步了!” 根泽尔和盖茨终于一起分享了2020年度物理学奖的另一半。
相对论和量子论是纯科学成功的范例,将20世纪塑造成了一个象征着科学的世纪,极大地推动了相关的技术革命,至今还影响着我们的生活,21世纪的诺贝尔物理学奖大多与这两种理论相关。多才多艺如达·芬奇的彭罗斯,他的研究为好奇心所驱动,并不讲究实际应用。彭罗斯的研究希望理解人类在宇宙中的位置,理解诸如黑洞那样的奥秘。在众多物理学家、天文学家的合作下,人类终于揭开了黑洞的神秘面纱。彭罗斯的独创性太强了,从而有人怀疑他是个离经叛道的人,对此他回答说:“对于基础物理学,我在大多数方面是相当保守的,与我所认识的大多数想在科学前沿获得进步的人相比,我更愿意接受传统智慧。”正是这种接受传统智慧并对宇宙充满好奇的品质,使得彭罗斯、根泽尔和盖茨终于取得了成功,不是吗?
[1]Penrose R,Rindler W. Spinor and twistor methods in spacetime geometry, Vol 2. Cambridge:Cambridge University Press, 1986.
[2]Penrose R. Cycles of time. London:The Bodley Head Ltd., 2010.
[3]Penrose R. Gravitational collapse and spacetime singularities. Physical Review Letters, 1965, 14(3): 57.
[4]An D, Meissner K A, Nurowski P , et al. Apparent evidence for Hawking points in the CMB sky, Monthly Notices of the Royal Astronomical Society, 2020, 495 (3): 3403.
[5]李新洲. 扭量理論. 自然杂志,1984(7): 9.
[6]李新洲.超越爱因斯坦. 科学,2015,67(6):15.
[7]Hao J G, Li X Z. Phantom cosmic dynamics: Tracking attractor and cosmic doomsday. Physical Review D, 2004, 70(4): 043529.
[8]Li X Z,Zhang J Z. Bound states of a fermion and a Dirac dyon in Robertson-Walker metric. Journal of Physics A, 1993, 26(17):4451.
关键词:彭罗斯 彭罗斯阶梯 奇点理论 ■

