岩金矿床资源储量估算品位域的确定及其意义
李红兵 高帮飞
摘要:资源储量估算一般在特定的品位域内进行,其核心是确定采用哪些已知数据对未知点进行估值。传统方法在确定样品数据的特异值时,过多考虑矿床的经济性而忽略了其地质特征和品位统计特征。在勘查数据分析基础上,引入分形分析、边界分析和变异函数分析,以确定资源储量估算的品位域及相关参数。案例分析表明,改进的IDW法估值流程深化了样品数据的地质特征、品位统计特征和经济属性之间的联系,融合了不同估值技术方法特点,为传统资源储量估算提供了新思路。
关键词:IDW法;勘查数据分析;分形分析;边界分析;变异函数分析;岩金矿床
中图分类号:TD11 P618.51文献标志码:A开放科学(资源服务)标识码(OSID):
文章编号:1001-1277(2021)04-0006-06doi:10.11792/hj20210402
资源储量估算的核心问题之一是确定采用哪些已知数据对未知点进行估值。理论上,特定矿化域内所有工程采样数据都应该参与资源储量估算[1]。但是,在实际操作中,为了减少特异值(包括特高值和特低值[2])对估值的影响,需要确定资源储量估算的品位域,即剔除具有特异值样品后的品位域[3]。该品位域作为后续勘查数据分析、边界分析及估值的基础。岩金矿床矿体金品位分布一般不均匀,较短距离内品位可能会有很大变化,即存在所谓的“块金效应”。因此,确定资源储量估算的合理品位域,对于准确评估岩金矿床的经济价值,科学分析特异值的分布特征及对估值影响,有着十分重要的理论和现实意义。本文以中亚某岩金矿床为例,探讨分形和地质统计学方法在确定资源储量估算品位域中的应用,在此基础上寻求基于距离幂次反比法(IDW)的资源储量估算流程的最佳实践。
1 成矿地质概况
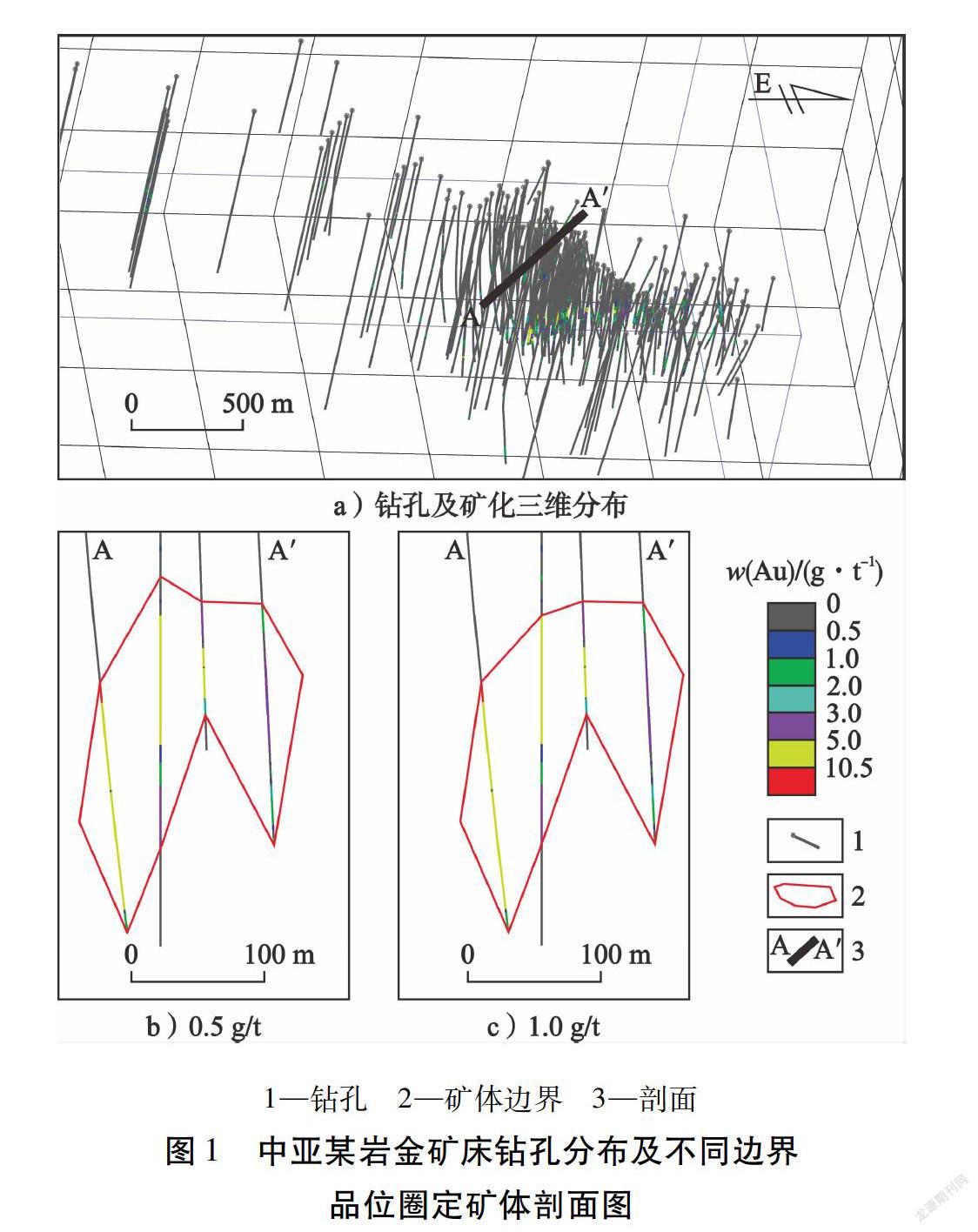
中亚某岩金矿床产于泥盆纪火山穹隆构造边缘。矿区出露地层包括变质杂岩和中基性火山-沉积岩,岩浆岩以三叠纪侵位的闪长岩、二长斑岩、辉绿岩等岩脉为主。该岩金矿床矿石类型可分为(细脉)浸染型、石英-电气石-硫化物型、块状硫化物型、方解石-硫化物脉型、稀疏浸染型,局部发育少量热液角砾岩型矿石。其中,(细脉)浸染型矿石主要产于二长斑岩内部,金品位较低,一般小于2 g/t;石英-电气石-硫化物型矿石发育于蚀变二长斑岩和变质地层中,金品位较高,一般为5~15 g/t,最高可达73 g/t。围岩蚀变广泛发育,常见硅化、绢英岩化、碳酸盐化、电气石化、泥化、绿泥石化、绿帘石化等。矿化产出明显受构造、岩性控制。主矿体产于北西向切层和顺层剪切带内,几乎不跨越剪切带;部分矿体受变质地层层间破碎带控制,顺层产出;少量矿体产于二长斑岩内或其内外接触带,受岩体侵入构造控制。主矿体走向北西西,倾向南西,倾角60°~70°,向北西倾伏,倾伏角30°~45°,长1 500 m,沿倾向延深1 000 m,厚10~80 m。截至2010年,该矿床累计施工地表钻孔274个(见图1),总进尺14万余m,分析样品1.7万件,品位为0.01~73.20 g/t,取样样长0.1~3.5 m。由于勘查阶段并非连续取样,因而存在大量缺省数据。
2 资源储量估算品位域的确定
圈定品位域进行资源储量估算是国内外的通行做法[4-7]。特高值样品在全部勘查数据中往往只是极少部分,但其对勘查数据统计结果影响极大;相反,在系统取样前提下,特低值样品数据往往较多,但大多数数据作为背景值不参与最终品位估值。因此,有必要对勘查数据中的特异值进行识别,减少其影响,以确保资源储量估算品位域内的样品数据同时具有地质和统计上的连续性。总的来看,特高品位识别和处理方法比较多,相对较为成熟[8-18],常用的有:①考虑偏离平均值程度的m+3σ法(m为平均值、σ为标准差)、变化系数法(σ/m)、估值邻域法;②根据偏离正常分布情况的影响系数法和十分位数分析法;③偏离正常分布曲线的拐点或断点作为判定依据的累计频率分布法、直方图法或概率分布图法、Cutting Curve图解法和97.5 %经验法等。特低值一般不进行处理,地质解译和矿体圈定多取决于地质工程师的认识和经验判断[7]。
本文通过采用分形方法来识别特异值,进而确定品位域。高帮飞等[3]通过实际案例对传统方法与分形方法进行对比分析,认为分形方法具有如下优点:①分形方法将地质特征与品位统计特征有机结合,既可以有效区分资源储量估算的品位域和特异值,又可以对矿化域细分出低品位域、中品位域和高品位域,与成矿作用的多期多阶段或多种矿化类型混合的特征相对应,给出品位分布的地质解释;②分形方法可以同时给出品位域的上限值和下限值(即特高值和特低值);③分形方法从全局考虑,适用于不同尺度、各种形式特高值的识别;④分形方法的可操作性和重复性强,人为因素相对较少,易于推广。前人已对该方法进行过详细介绍[3,19-21],此处不再赘述,直接给出统计分析结果。
2021年第4期/第42卷黄金地质黄金地质黄 金
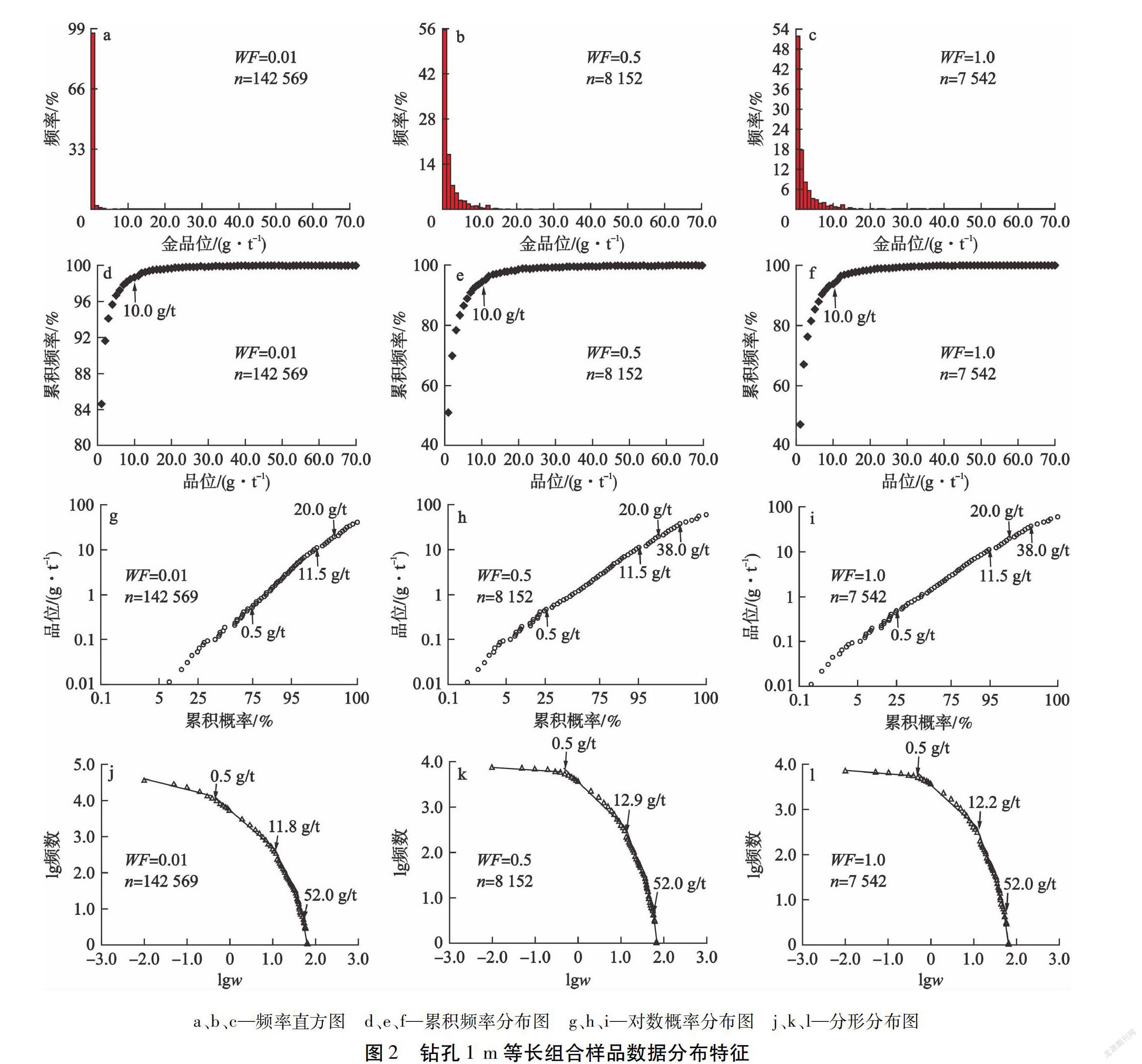
分别以所有钻孔数据(未实际圈矿,相当于以0.01 g/t为边界品位,即WF(Wire Frame,线框)=0.01)、0.5 g/t(WF=0.5)、1.0 g/t(WF=1.0)为边界品位,钻孔1 m等长组合样品数据分布特征见图2(箭头指示特征拐点或断点)。由图2可知,因品位數据范围较大(0.01~69.00 g/t),所确定的品位域内全部组合样品数据的直方图无法进行合理分组和呈现特异值(见图2-a、b、c)。累积频率分布图(见图2-d、e、f)给出完全一致特征拐点(10.0 g/t)。对数概率分布图(见图2-g、h、i)提供的信息较为丰富,组合样品数据均呈近似对数正态分布,特征拐点或断点分别为0.5 g/t、11.5 g/t、20.0 g/t和38.0 g/t。分形分布的结构较为稳定,按照拟合优度(R2)大于0.96 来考虑,组合样品数据的特低值为0.5 g/t,特高值为52.0 g/t,分形区间为0.5~52.0 g/t,可以直接作为资源储量估算的品位域。进一步细分品位域,不难发现,中、高品位域的特征拐点为12.0 g/t左右,变化于11.8~12.9 g/t(见图2-j、k、l,w为品位)。
3 基于品位域的边界分析
开展品位域边界分析的目的是区分品位域的边界条件为“硬边界”或“软边界”。估算品位域的边界条件是利用边界两侧的品位变化特征来确定:硬边界内外的品位存在突变,而软边界附近的品位呈现出渐变趋势[1,7,22-23]。硬边界条件下,意味着品位域内矿块品位的估值仅采用品位域内样品数据;软边界条件下,允许品位估值采用落入搜索椭球内的所有数据,而不考虑这些样品数据是否在品位域内[7,24]。
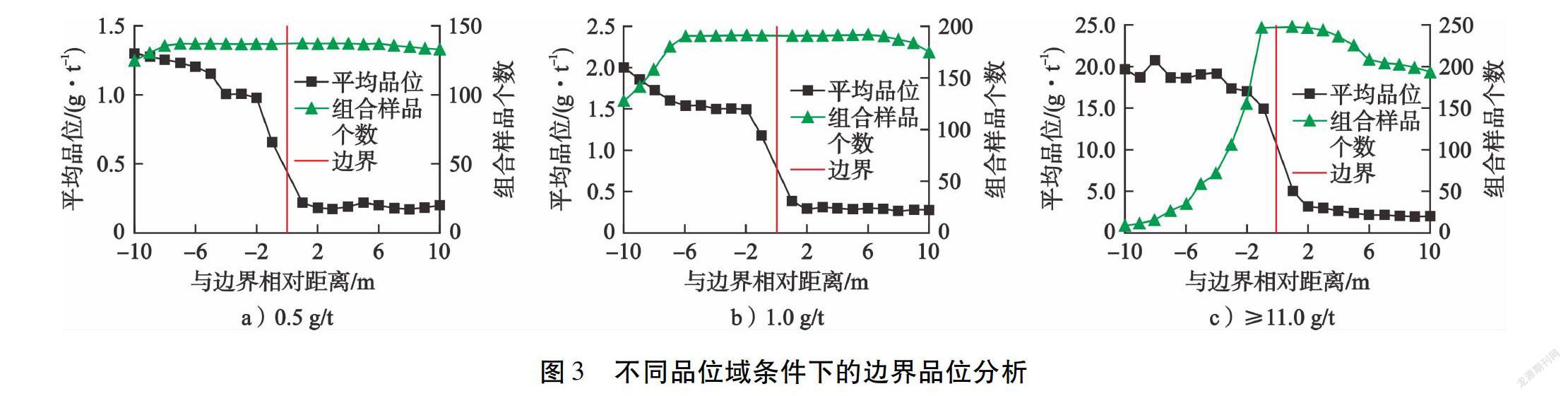
边界分析是统计意义上的。考察了274个钻孔在0.5 g/t(品位域下限/矿化边界品位)、1.0 g/t(一般工业指标)和≥11.0 g/t(近似中、高边界品位)3种情况下的边界品位分析,结果见图3。由图3-a)可知,以0.5 g/t为边界品位时,品位域内样品(与边界的距离为负)品位由远到近,没有显著降低,但与品位域外样品(与边界的距离为正)较为稳定的0.2 g/t有明显差异,为硬边界条件。同理,可以得出1.0 g/t和≥11.0 g/t 的边界品位亦为硬边界条件(见图3-b)、c))。因此,无论采用上述哪种边界品位圈定矿(化)体,资源储量估算时仅能采用品位域内的样品数据。此外,从参与统计的组合样品个数来看,以0.5 g/t为边界品位情况下,品位域内外参与统计的组合样品个数相当(见图3-a));以1.0 g/t为边界品位情况下,品位域内距边界7~10 m的组合样品数量有所减少(见图3-b));以≥11.0 g/t为边界品位情况下,与边界距离越远,组合样品数量呈明显下降趋势(见图3-c))。这一结果显示:随着域边界品位的提高,相应矿(化)体厚度具有明显减小趋势。
4 块金效应与IDW法幂次确定
块金效应是地质统计学术语,用于描述微小尺度范围内样品点间的变异性,通常用块金方差与总方差的比值来表示[25]。变异函数揭示了样品在取样间距尺度的变异性,可以提供较为准确的块金效应信息[1]。与块金效应相关的另一个地质统计学概念为屏蔽效应。屏蔽效应是指距离待估矿块较近的样品点对距离较远的样品点的屏蔽作用,从而在对矿块进行品位估值时,使距离较近样品点的贡献更大。屏蔽效应与块金效应密切相关[26-30]:当块金效应很小或者不存在时,已知样品点的克里格权重系数受屏蔽效应影响;当块金效应增大,屏蔽效应相应减弱;当显示为纯块金效应时,所有样品点相互独立,权重系数相等,屏蔽效应消失。
IDW法中样品权重的确定并不受屏蔽效应影响[30],而和待估值矿块与已知样品点的距离和估值时幂次选择有关。对于IDW法而言,随幂次增大,与待估值点越近的样品点权重就会越大[24],类似屏蔽效应。因此,IDW法估值参数中的幂次,与克里格估值法中的块金效应可能有着内在联系。基于上述讨论,本文尝试将克里格估值法中的块金效应原理应用于IDW法估值参数选取,即根据变异函数分析块金效应的大小,来确定IDW法幂次取值。经验表明,块金效应较小时,适宜采用较大的幂次[26]。具体而言,若变异函数块金效应越小,则屏蔽效应越强,IDW法幂次选择3~5,邻域范围适当缩小,可与变程相当;反之若块金效应大,则屏蔽效应弱,IDW法幂次选择1~2,邻域范围应适当扩大;当存在纯块金效应时,IDW法幂次设为0,各样品点权重相同,与距离无关,估值领域范围可以扩大到整个品位域。
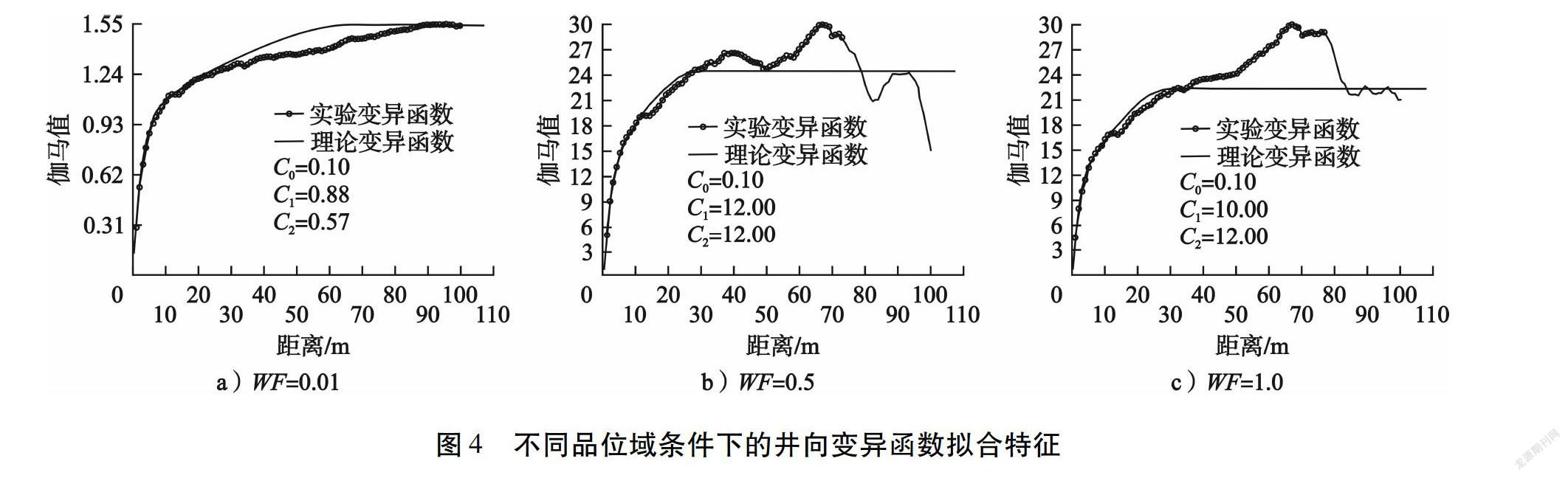
通过对该岩金矿床经特高值处理后的样品数据进行1 m等长组合,开展块金效应分析。在WF=0.01、WF=0.5和WF=1.0品位域条件下的井向变异函数拟合特征见图4。根据C0/(C0+C1+C2)(C0为块金值,C1为第一结构组分方差,C2为第二结构组分方差)得到这3种条件下的块金效应分别为6.45 %、0.41 %和0.45 %,显示出较低的块金效应特征。因此,采用IDW法估值时搜索半径不宜过大,幂次取5。为了对比分析,考虑了不同边界品位(0.5 g/t和1.0 g/t)和不同幂次(5和2)条件下的品位估值。
5 估值结果比较
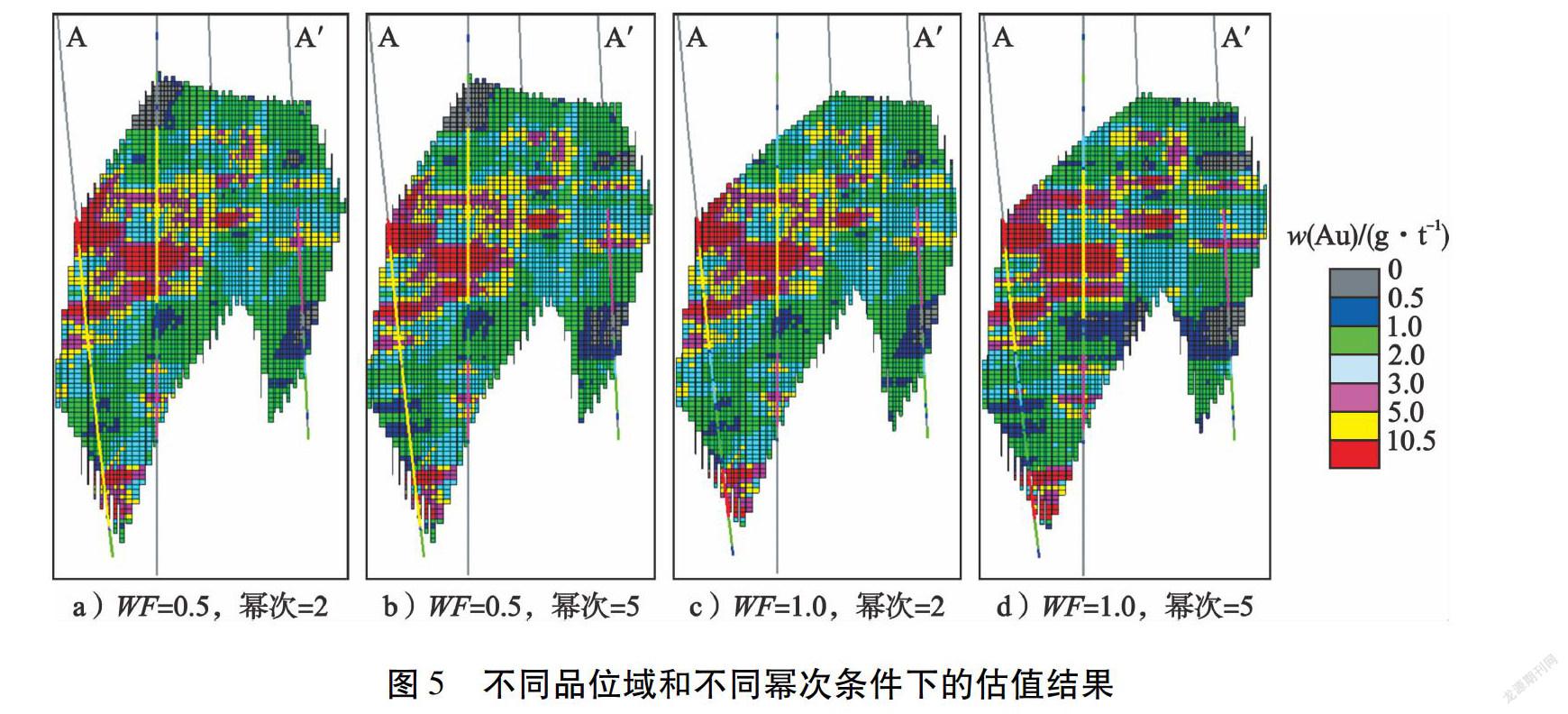
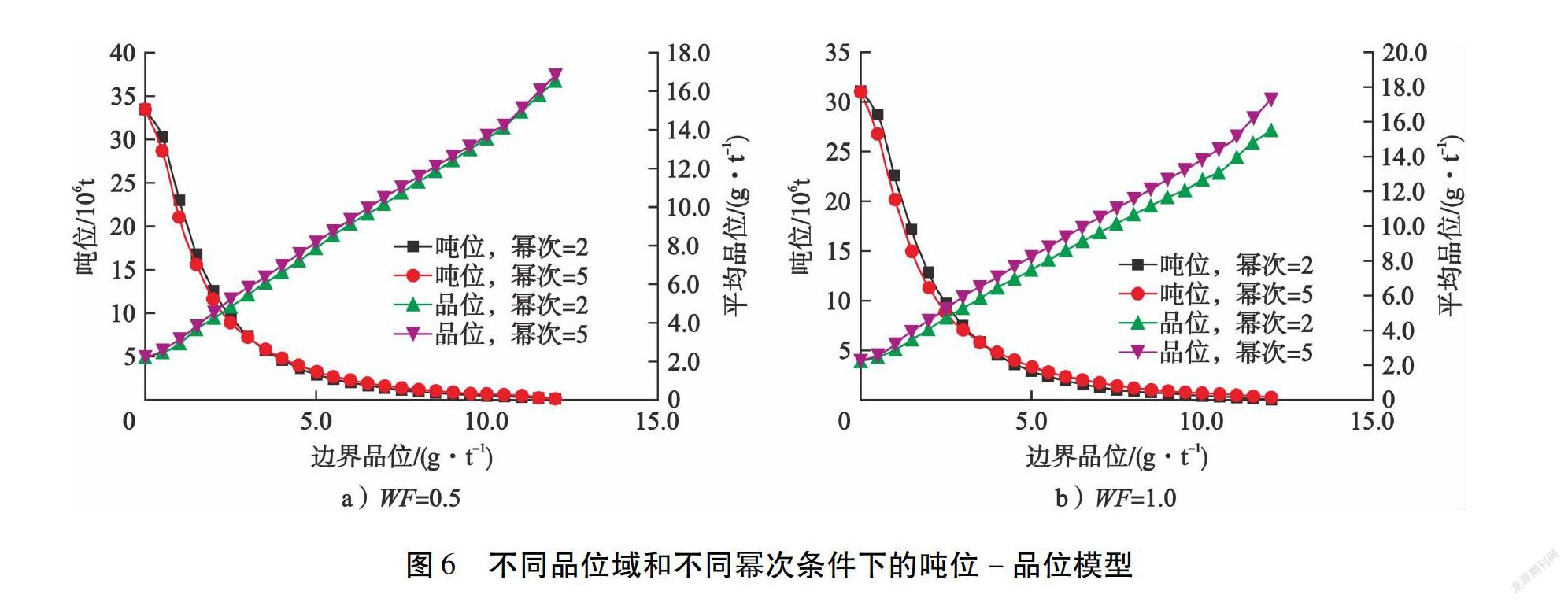
该岩金矿床WF=0.5和WF=1.0的2种品位域及IDW法幂次为2和5的估值矿块模型结果见图5,其吨位-品位模型见图6。随着圈矿边界品位的提高,整个矿体的吨位呈下降趋势,而平均品位呈上升趋势;同一品位域,随着IDW法幂次增加,呈现吨位下降、平均品位增加的趋势(见图6)。从矿块模型可以直观看出,IDW法幂次为2时,以0.5 g/t为边界品位和以1.0 g/t为边界品位得到的矿块模型估值结果,呈现出相似的矿化和夹石分布规律(见图5-a)、c))。随着幂次由2增加到5,高品位矿化段及夹石的连续性增强、范围变大(见图5-b)、c)、d))。以1.0 g/t为边界品位、幂次从2增加到5的影响,较以0.5 g/t为边界品位时的影响要大很多(见图5)。吨位-品位模型也呈现这一特点,即圈矿品位提高,幂次增加对吨位下降和平均品位增加的影响显著(见图6)。
6 讨 论
6.1 品位域的经济属性
采用分形方法确定资源储量估算域,是依据样品在统计意义上的一致性,而没有直接考虑其经济上的可行性。行业标准推荐的一般做法是,采用一般工业指标或者经设计单位可行性研究后,确定矿体圈定的边界品位(传统方法不存在确定特低品位的问题),剔除特高品位后,得出最终资源储量估算的品位域。本文做法与行业标准并不矛盾。不同的是,本文品位域的确定重点考虑矿化的地质连续性和品位空间连续性,而后续资源储量估算结果报告可以参照一般工业指标或可行性研究结果确定的边界品位。先考虑地质性,再考虑经济性,也与矿化体圈定和资源储量估算的基本原则相符[7]。
6.2 特高值与高品位矿段
該岩金矿床品位大于1.0 g/t原始样品点3 364个,其平均品位4.29 g/t,标准差5.72,变化系数133 %。按6倍平均值计算,特异值为25.74 g/t,涉及到 48个样品点;按m+3σ计算,特异值为21.45 g/t,涉及到64个样品点。采用分形方法确定矿床存在以12.0 g/t为边界品位的高品位矿段,其特异值为52.00 g/t,仅涉及到4个样品点,几乎所有高品位样品数据均参与了估值。高品位矿段是否可以作为混合总体的一个单独组分,可以运用总体筛分方法来确定[31]。当存在高品位组分时,将高品位值当作特高品位剔除,无疑会降低该矿床的经济性。条件允许的情况下,应单独圈定高品位矿体,以减少对相邻区域估值影响。如果确为特高品位或者无地质依据判断时,可以采用对数正态克里格法、指示克里格法、概率克里格法或限制克里格法直接进行品位估值,而不用剔除特高品位矿段[6,8,32-34]。
6.3 夹石和缺省值
矿体中存在夹石或因非连续取样导致样品值缺省,在资源储量估算案例中十分常见。规范推荐做法是当夹石达到一定厚度时剔除。然而,已经圈入矿化域的低品位样品已成为矿化域的组成部分,这部分样品值给整体品位变异性带来的影响是客观存在的,人为去除低品位样品,使得结果趋向于“理想的高品位”是危险的[35]。从本文的案例中也可以看出,通过设置合适的参数,夹石的形态、范围可以较好的估计和呈现,而无需专门处理。
6.4 改进的估值流程
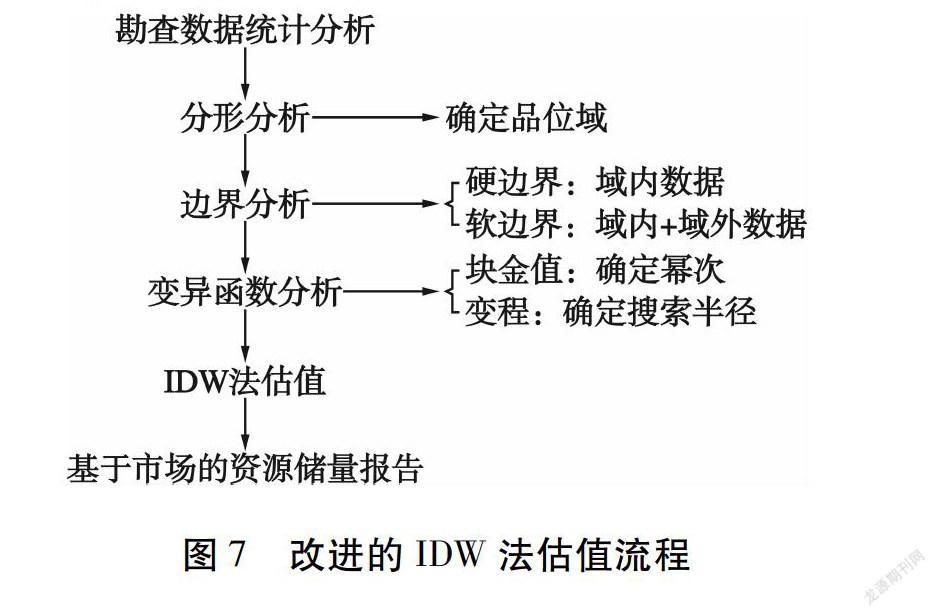
改进的IDW法估值流程见图7。在传统勘查数据统计分析基础上,引入了分形分析、边界分析与变异函数分析。分形分析的目的是确定资源储量估算的品位域,减少特异值处理的人为干扰。对品位域进行边界条件分析,用以确定估值时所采用数据与品位域的关系,硬边界条件下仅采用域内数据,而软边界条件下可以采用落入搜索椭球内的所有数据。变异函数分析可以提供IDW法估值的关键参数:幂次和距离。在上述数据分析基础上,开展基于品位域的IDW法估值。估算结果可以结合市场行情、矿山实际生产条件和长远规划,考虑不同边界品位,确定相应的矿石吨位-品位。因此,该方法的优点在于既考虑了样品数据的地质性和统计特征,又结合了矿业开发的经济性。
7 结 论
1)分形方法可以有效确定资源储量估算的品位域,同时给出特高值和特低值,方法稳定,可操作性强。
2)品位域的边界分析进一步明确了估值时所采用数据与品位域的关系。硬边界条件下,估值仅采用品位域内样品数据;软边界条件下,则可以采用落入搜索椭球内的所有数据。
3)在上述分析基础上,尝试将克里格估值法中的块金效应原理应用于IDW法估值参数选取。改进的IDW法估值流程深化了样品数据的地质特征、品位统计特征和经济属性之间的联系,融合不同估值技术方法特点,为传统资源储量估算提供了新思路。
[参 考 文 献]
[1]ROSSI M E,DEUTSCH C V.Mineral resource estimation[M].Berlin:Springer,2014.
[2]罗晓峰.非稳健品位厚度集的确定——特高品位厚度及特低品位厚度的确定[J].新疆有色金属,1991(1):3-9.
[3]高帮飞,谢徽,沈阳,等.一种确定资源储量估算的品位域的方法:CN201611040814.3[P].2017-05-31.
[4]STEGMAN C L.How domain envelopes impact on the resource estimate—case studies from the Colar gold field NSW,Australia[C]∥EDWARDS A C.Mineral resource and ore reserve estimation—the AusIMM guide to practice.Victoria:the Australasian Institute of Mining and Metallurgy,2001:221-236.
[5]ABZALOV M Z,HUMPHREYS M.Resource estimation of structurally complex and discontinuous mineralization using nonlinear geostatistics:case study of a mesothermal gold deposit in northern Canada[J].Exploration and Mining Geology,2002,11(1/2/3/4):19-29.
[6]EMERY X,ORTIZ J M.Estimation of mineral resources using gradedomains:critical analysis and a suggested methodology[J].The Journal of the South African Institute of Mining and Metallurgy,2005,105:247-255.
[7]高幫飞.资源量估算的边界分析与矿化体圈定[J].地质与勘探,2018,54(2):415-425.
[8]PARKER H M.Statistical treatment of outlier data in epithermal gold deposit reserve estimation[J].Mathematical Geology,1991,23(2):175-199.
[9]侯景儒,张树泉,黄竞先.特异值的识别、处理及块段平均品位估计[J].地质找矿论丛,1990,5(3):93-103.
[10]丁旭东.几种特异值处理方法的比较[J].物探化探计算技术,1996,18(1):71-77.
[11]刘振升.河台金矿床特高品位及成矿富集规律研究[J].黄金,2001,22(3):11-14.
[12]SINCLAIR A J,BLACKWELL G H.Applied mineral inventory estimation[M].Cambridge:Cambridge University Press,2002.
[13]MARINHO M,MACHUCA M.Capping and outlier restriction:stateofart[C]∥The Canadian Institute of Mining,Metallurgy and Petroleum.Proceedings of APCOM.Vancouver:the Canadian Institute of Mining,Metallurgy and Petroleum,2009:337-345.
[14]林吉飛,陈日辉,李德,等.一种识别及处理特高品位值的新方法[J].矿冶,2011,20(3):36-41.
[15]NOWAK M,LEUANGTHONG O,SRIVASTAVA R M.Suggestions for good capping practices from historical literature[C]∥X-CD Technologies Inc.Proceedings of the 23rd world mining congress 2013.Montreal:Canadian Institute of Mining,Metallurgy and Petroleum,2013:1-10.
[16]王丽艳.内蒙古白音查干锌多金属矿资源量估值中特高品位的识别和处理[J].中国矿山工程,2014,43(3):17-20.
[17]任萌,胡乃联,李国清,等.储量估算中特高品位识别与处理方法研究[J].矿业研究与开发,2014,34(3):112-117.
[18]LEUANGTHONG O,NOWAK M.Dealing with highgrade data inresource estimation[J].The Journal of the Southern African Institute of Mining and Metallurgy,2015,115(1):27-36.
[19]BLENKINSOP T G.Cataclasis and processes of particle size reduction[J].Pure and Applied Geophysics,1991,136(1):59-86.
[20]TURCOTTE D L.Fractals and chaos in geology and geophysics[M].Cambridge:Cambridge University Press,1992.
[21]高帮飞,陈志广,孙刚,等.内蒙古常福龙金矿床Au品位分布特征及其地质意义[J].黄金,2012,33(9):9-12.
[22]WILDE B J,DEUTSCH C V.Kriging and simulation in presence of stationary domains:developments in boundary modeling[C]∥ABRAHAMSEN P,HAUGE R,KOLBJФRNSEN O.Geostatistics Oslo 2012.Berlin:Springer,2012:289-300.
[23]ABZALOV M Z.Applied mining geology[M].Berlin:Springer,2016.
[24]DOMINY S C,ANNELS A E,PLATTEN I M,et al.A review of problems and challenges in the resource estimation of high Nugget-effect lodegold deposits[C]∥SIMON D.Proceedings of 5th international mining geology conference.Melbourne:the Australasian Institute of Mining and Metallurgy,2003:279-298.
[25]ANNELS A E.Mineral deposit evaluation:a practical approach[M].London:Chapman and Hall,1991.
[26]JOURNEL A G,HUIJBREGTS C J.Mining geostatistics[M].San Diego:Academic Press INC,1989.
[27]DEUTSCH C V.Correcting for negative weights in ordinary kriging[J].Computers and Geosciences,1996,22(7):765-773.
[28]ARMSTRONG M.Basic linear geostatistics[M].Berlin:Springer,1998.
[29]ELLIOTT S M,SNOWDEN D V,BYWATER A,et al.Reconciliation of the McKinnons Gold Deposit,Cobar,New South Wales[C]∥EDWARDS A C.Mineral resource and ore reserve estimation—the AusIMM guide to practice.Melbourne:the Australasian Institute of Mining and Metallurgy,2001:257-268.
[30]WACKEMAGEL H.Multivariate geostatistics:an introduction with applications[M].Third edition.Berlin:Springer,2003.
[31]MALEKI M,MADNI N,EMERY X.Capping and kriging grades with longtailed distributions[J].The Journal of the Southern African Institute of Mining and Metallurgy,2014,114:255-263.
[32]JOURNEL A G,ARIK A.Dealing with outlier high grade data in precious metals deposits[C]∥FYTAS K,COLLINS J L,SINGHAL R K.Proceedings of computer application in the mineral industry.Boca Raton:CRC Press,1988:161-171.
[33]ARIK A.Outlier restricted kriging:a new kriging algorithm for handling of outlier high grade data in ore reserve estimation[C]∥KIM Y C.Proceedings of the 23rd international symposium on the applicationof computers and operations research in the minerals industry.Littleton:Society for Mining,Metallurgy,and Exploration,1992:181-187.
[34]COSTA J F.Reducing the impact of outliers in ore reserves estimation[J].Mathematical Geology,2003,35(3):323-345.
[35]孫玉建.地质统计学在固体矿产资源评价中的若干问题研究[D].北京:中国地质大学(北京),2008.
Delineation of the grade domain for mineral resource
and reserve estimation of rock gold deposits and its significance
Li Hongbing1,Gao Bangfei2
(1.International Division of Zijin Mining Co.,Ltd.;2.China Railway Resources Group Co.,Ltd.)
Abstract:Mineral resource and reserve estimation is generally carried out in a specific grade domain,and the essential issues are to determine which known data should be used to estimate unknown points.When fixing the extreme value of sample data,the traditional method takes too much consideration of the economics of the deposit andneglects its geological and statistical characteristics.Based on the exploration data analysis,this paper introduces fractal analysis,boundary analysis and variogram analysis to determine the estimated grade domain and related parameters of mineral resource and reserve estimation.Case study shows that the improved IDW estimation flowsheet has deepened the relationship among the geological characteristics,grade statistical features and economic properties of the sample data.Furthermore,the integration of different techniques and methods provides new ideas for the traditional mineral resource and reserve estimation.
Keywords:IDW method;exploration data analysis;fractal analysis;boundary analysis;variogram analysis;rock gold deposit

