基于多稳随机共振的机电设备故障诊断研究

王谊

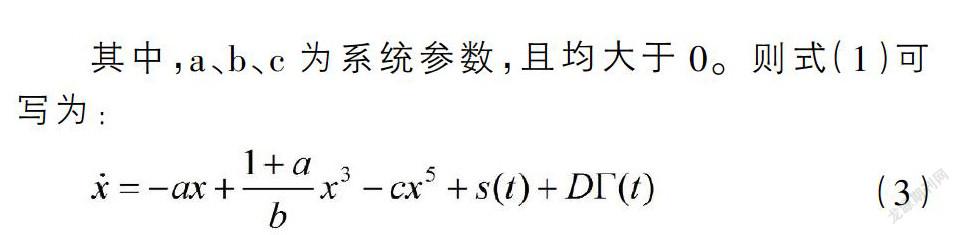
摘要：针对机械轴承早期故障诊断提出了多稳随机共振检测方法。分析了系统参数对多稳系统结构的影响，研究了高斯噪声背景下基于多稳随机共振的微弱信号检测方法。采用平均输出信噪比作为衡量指标，以多频微弱信号为待测信号进行数值仿真，并将其应用于滚动轴承故障信号检测中，实验结果均表明，该方法对早期故障振动信号具备准确的诊断能力，为其应用于工程实践奠定了基础。

Abstract： A multi-stable stochastic resonance detection method is proposed for early fault diagnosis of electromechanical equipment. The effect of the system parameters on the structure of the multi-stable system is analyzed， and the weak  signal detection method based on multi-stable stochastic resonance in the Gaussian noise background is studied. The average output signal-to-noise ratio is used as a measurement index， and the multi-frequency weak signal is tested for numerical simulation. The method is applied to the rolling bearing failure signal detection. The experimental results show that the method has accurate diagnosis ability for early fault vibration signals， which lays the foundation for its application in engineering practice.

關键词：多稳态随机共振;故障诊断;机电设备

Key words： multi-stable stochastic resonance;fault diagnosis;electromechanical equipment

中图分类号：TK407                                      文献标识码：A                                  文章编号：1674-957X（2021）06-0145-02

0  引言

近年来，随着智能制造技术的迅速发展，机械设备向着大型、精密化发展，设备结构之间的耦合越来越强，其动态行为越来越复杂。同时，机械结构的故障会带来较大的经济损失和人员伤亡，因此机械轴承早期故障监测具有重要的工程应用价值。

随机共振是目前使用较为广泛的非线性检测方法[1]。单稳态与双稳态随机共振在机械故障诊断、超声信号检测及图像增强等领域有诸多应用[2-4]。但在待测信号非常弱的条件下，以上两种方法的检测效果较差，因此多稳态随机共振的研究逐渐开展。本文通过研究多稳态随机共振对于高频多频信号的检测效果，并将其应用于滚动轴承的振动故障检测。

1  多稳随机共振模型

多稳随机共振模型可用具有三势阱性质的非线性郎之万方程来描述[5]，其实质为一个过阻尼粒子受到外作用力和外加噪声同时作用下在三个势阱中所做的运动。其数学模型如下：

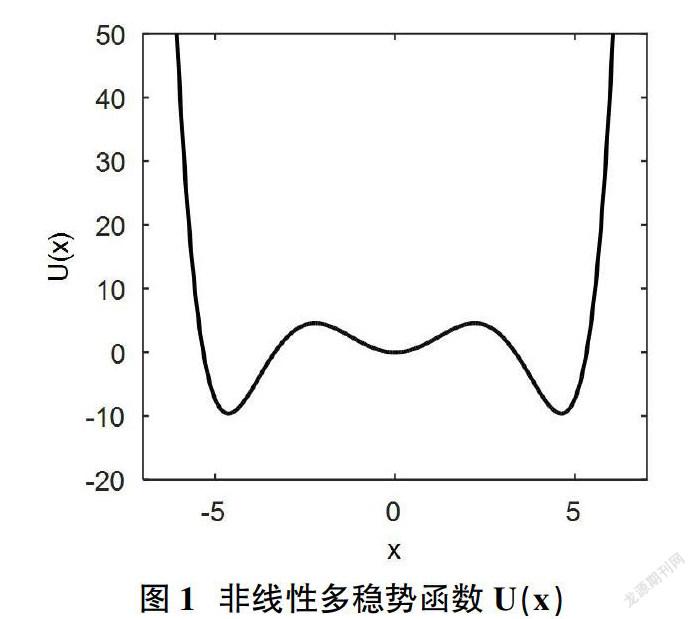
多稳态势函数U（x）如图1所示。由式（2）可知，不同的系统参数a、b、c的取值影响势函数U（x）的结构，即系统会在单稳态、双稳态及三稳态之间互相切换。由于多稳态系统比单稳和双稳具有更好地检测能力，所以在系统参数选取时需避免单稳态和双稳态的出现[6-8]。

2  工程应用

本文采用的轴承内圈故障信号数据来自凯斯西储大学轴承数据官网[9]，实验轴承为深沟球轴承6205-2RS JEM SKF，如图2所示。

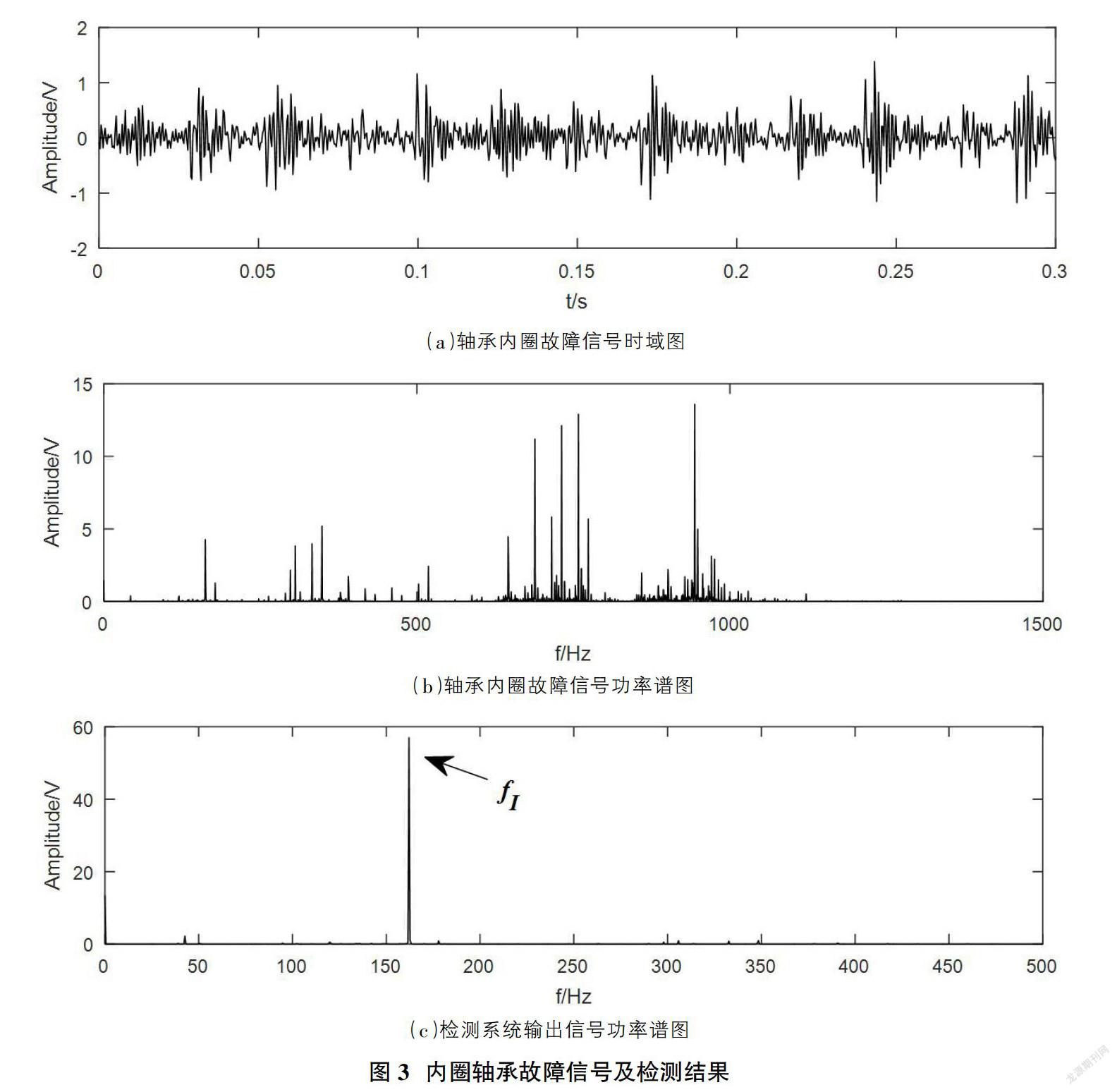
该轴承滚珠个数为9，转速1797r/min，其内轴故障特征频率为162.08Hz。通过本文提出的多稳态随机共振检测方法，轴承故障信号检测结果如图3所示。

由图3中可以看出，输出信号的时域波形呈现一定的周期性，且在频率为162.1Hz处有明显峰值，其频率与理论轴承内圈故障信号的频率基本一致。实验结果说明该滚动轴承的故障类型是内圈故障。

3  结论

本文将多稳态随机共振检测方法应用于机械轴承早期故障信号的检测。介绍了多稳随机共振模型，分析了系统参数a、b、c对系统结构的影响。以平均输出信噪比为衡量指标，仿真实现了对多频高频微弱信号的检测。并将其应用于单晶炉振动信号检测，实验证明该方法能够有效实现机械轴承早期故障的诊断。

参考文献：

[1]Ji S Y， Yuan F， Chen K Y， et al. Application of stochastic resonance technology in underwater acoustic weak signal detection[C]. Oceans. IEEE， 2016： 1-5.

[2]张刚，胡韬，张天骐.基于随机共振大参数微弱周期信号检测[J].科学技术与工程，2015，15（35）：182-192.

[3]行鸿彦，卢春霞，张强.自适应随机共振微弱信号检测[J].系统仿真学报，2018，2（30）：587-604.

[4]殷学杰，马玉梅，潘振宽.基于饱和系统随机共振的图像去噪算法[J].计算机与现代化，2019（12）：44-48.

[5]胡茑庆.随机共振微弱特征信号检测理论与方法[M].北京：国防工业出版社，2012：42-46.

[6]Yi Wang， Shangbin Jiao， Qing Zhang， Shuang Lei， Xiaoxue Qiao. A weak signal detection method based on adaptive parameter-induced tri-stable stochastic resonance[J]. Chinese Journal of Physics， 2018， （56）： 1187-1198.

[7]Liu Y， Liang J， Jiao S B， et al. Stochastic resonance of a tri-stable system with α stable noise[J]. Chinese Journal of Physics， 2017， 55： 355-366.

[8]冯毅，陆宝春，张登峰.基于多稳态随机共振的轴承微弱故障信号检测[J].振动、测试与诊断，2016，36（6）：1168-1174.

[9]凯斯西储大学轴承故障官网[DB/OL].http：//csegroups. case. edu/ bearingdatacenter/ pages/12k-drive-end-bearing-fault-data.