未知环境下改进变步长蚁群算法的机器人路径规划*

徐玉琼，娄 柯，李志锟

(1.广州大学松田学院 电气与汽车工程学院，广东 广州 511370；2.高端装备先进感知与智能控制教育部重点实验室，安徽 芜湖 241000；3.安徽工程大学 安徽省电气传动与控制重点实验室，安徽 芜湖 241000)

0 引 言

路径规划技术[1～3]是移动机器人研究领域的核心技术之一，它是指移动机器人在有障碍物的环境中，从起点运动到终点搜索出一条最优的安全路径。为了解决移动机器人路径规划问题，国内外学者提出诸多算法，如遗传算法(GA)、A*算法[4,5]、蚁群算法(AG)[6～10]、狼群算法[11]等。随着群智能算法的不断创新，传统蚁群算法在路径规划技术方面成果显著。然而，传统蚁群算法存在鲁棒性不强、死锁、搜索停滞等问题急需被解决。针对传统蚁群算法相关缺陷，大量国内外学者深入研究，提出诸多改进蚁群算法。文献[12]利用人工势场法[13]的优势，与蚁群算法进行结合，加快了算法的收敛速度，但其适应不了复杂环境。文献[14]为了解决蚁群算法容易陷入局部最优、收敛速度与寻优能力不平衡等问题，提出了自适应蚁群算法，针对信息素的分配重新制定策略，设置迭代阈值，使得算法在寻优后期也具有一定的搜索能力；但该算法转折点较多，降低算法搜索效率。文献[15]利用双向搜索机制以及对启发函数设置比例系数引导因子进行改进，有效改善了移动机器人目标性不强，向目标相反方向移动的问题，但算法路径冗长，寻优能力较低。相关改进蚁群算法相对于其他群智能算法能搜索出较优路径，但依然耗时较长、收敛较慢，很难搜索出最优路径。

针对以上问题，本文对蚁群算法作出相应改进，提出了改进变步长蚁群算法应用于移动机器人的路径规划。

1 环境建模

本文设定移动机器人在二维栅格环境下进行路径规划。障碍物的高度忽略不计，所有栅格尺寸均为1 m×1 m的正方形，空白栅格为自由栅格，在仿真程序中用0表示，黑色栅格为障碍物栅格，在仿真程序中用1表示。如图1所示，该栅格地图环境为20 m×20 m的正方形，由若干个障碍物组成，起点坐标为(0.5,19.5),终点坐标为(19.5,0.5)，移动机器人需要从起点到终点规划处一条最优路径。

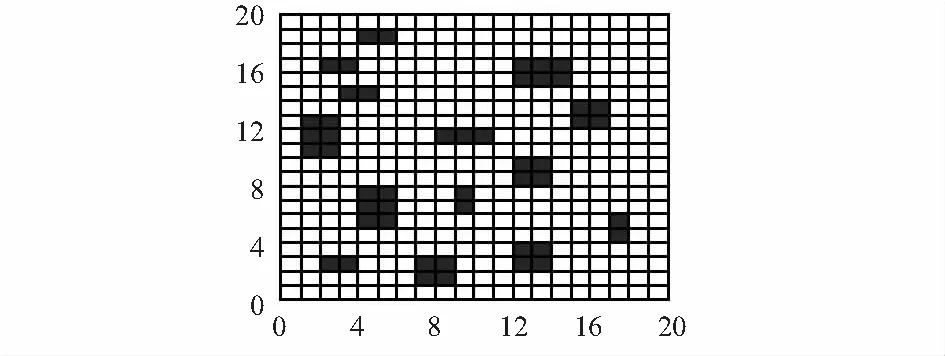
图1 栅格地图

2 改进变步长蚁群算法

2.1 改进平滑度机制

本文引入平滑度函数，对多次转角的位置平滑处理，缩短移动机器人路径长度，减少移动机器人路径规划过程中产生的转折次数。改进后的路径选择概率公式如下

(1)

(2)

(3)

(4)

式中γij(t)为移动机器人从位置i到位置j的转折启发函数；σ为转折启发因子，取值为正整数；θ为当前位置i到位置j的连线与起点到终点的连线之间的夹角，夹角越小，则线路的节点被选择的概率就越大，移动机器人规划出来的路径越逼近于最优路径；α表征信息素重要程度；β表征启发函数重要程度；τij表征路径(i,j)上的信息素浓度；allowed为移动机器人所有可能到达节点的集合；ηij为启发函数；f(θ)为平滑度引导函数；h为引导因子，引导节点向最优路径靠近，提高移动机器人搜索效率；(ix,iy)及(jx,jy)分别为当前节点与下一个节点的坐标。

加入平滑机制的路径规划效果如图2所示，路线{1,2,3,4,5}为传统蚁群算法路径规划图，路线{1,3,4,5}为加入平滑机制后的路径规划图，不难看出，后者转折点更少，路径长度也更短。因此，加入平滑机制后的蚁群算法可以显著提高路径规划质量，有效减少移动机器人转折次数以及缩短路径长度。

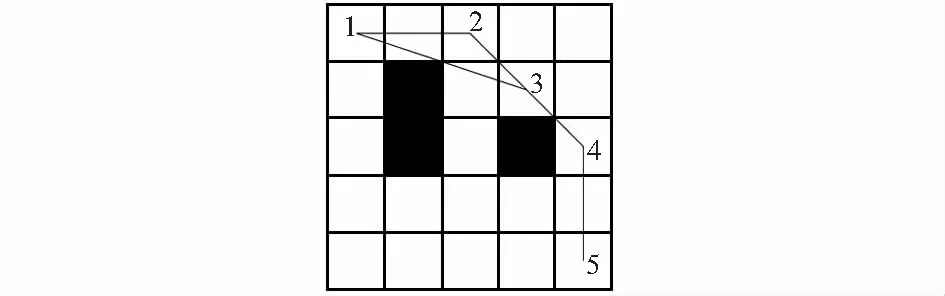
图2 平滑机制路径规划

2.2 改进蚁群系统

为了避免蚁群算法过早收敛于非最优解，蚁群系统对每条路径上的信息素设定阈值。当某条路径信息素浓度超过最大值时，则该条路径信息素浓度强制设置为τmax；当某条路径信息素浓度低于最小值时，则该条路径信息素浓度强制设置为τmin。移动机器人每次迭代后，对每条路径上的信息素作全局更新，公式如下

(5)

(6)

以上可以避免部分路径上的信息素浓度过高或者过低，避免产生部分蚂蚁过分集中在一条非最优路径，加长路径长度；但同时也可能限制最优路径上的信息素浓度，使蚁群收敛速度减慢甚至不能找出最优路径。

由图2可以看出，蚂蚁从起点1到节点3比起点1经过节点2再到节点3路径更短，转折点也更少，因此，路径{1,3}比路径{1,2,3}更重要。将这条最优路径用Eb来表示，所以应该加强路径{1,3}的信息素浓度，同时降低路径{1,2,3}的信息素浓度。为了解决蚁群算法在面对实际搜索的复杂性与信息素更新之间的矛盾，将路径{1,3}进行信息素强化，对其每条路径增加信息素c/Lb，则改进后的信息素更新公式如下

(7)

(8)

式中c为信息素增量参数，Lb为Eb的长度，Q为常量，表示信息素增强强度的系数，Lbest为全局最优解。当蚁群算法陷入局部最优或连续迭代3次没有改变最优路径长度时，设计信息素惩罚函数

(9)

式中L1为起点到终点的直线距离，L2为当前移动机器人从起点到终点路径规划的总长度，有效避免凹形障碍物周围信息素浓度过高，移动机器人陷入死锁现象。

3 算法仿真

在MATLAB R2018a平台构建仿真环境，分别对传统蚁群算法、文献[15]算法、本文算法进行仿真实验。为了保证实验的公平性，对以上算法均采用一样的栅格地图，移动机器人遇到障碍物时不能通过，可以在空白栅格自由移动。算法仿真结果如图3～图5所示，实验数据如表1所示。这里主要考察移动机器人路径长度、收敛速度、平滑度三个指标。

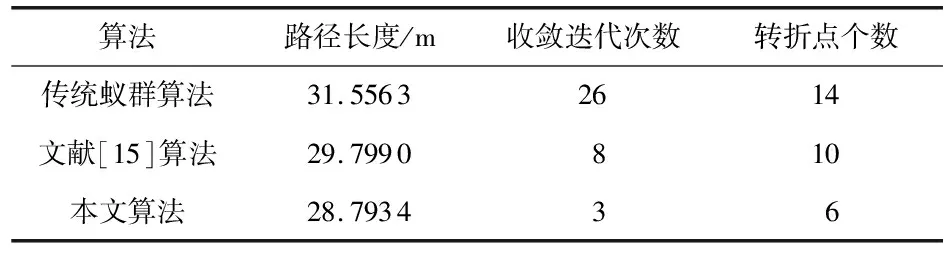
表1 仿真结果对比

其中，图3(a)为传统蚁群算法的移动机器人运动轨迹，路径长度为31.5 563 m，转折点为14个；图4(a)为文献[15]算法的移动机器人运动轨迹，路径长度为29.7 990 m，转折点为10个。文献[15]算法相较于传统算法在路径长度和平滑度两方面均有提升，但两种算法的平滑度依然不够，且两种算法的路径规划长度均过长。图5(a)为本文算法的移动机器人运动轨迹，路径长度为28.7 934 m，转折点为6个，本文算法引入平滑度引导函数，对转折位置较多的地方平滑楚理，诱导移动机器人朝向步长更大的节点移动。因此，本文算法规划出的路径比较平滑，相较于传统蚁群算法及文献[15]算法在路径长度方面分别缩短了8.8 %及3.4 %，证明了本文算法在路径规划方面明显优于其他两种算法。

图3(b)为传统蚁群算法收敛迭代曲线图，传统蚁群算法各代最优路径不够稳定，收敛迭代次数为26次；图4(b)为文献[15]算法收敛迭代曲线图，收敛迭代次数为8次，虽然相对于传统蚁群算法有一定的提升，但是收敛速度依然较慢，降低移动机器人搜索效率；图5(b)为本文算法收敛迭代曲线图，收敛迭代次数为3次，本文算法在移动机器人路径寻优过程中，找出各代局部最优路径，加强该路径信息素浓度，提高算法的收敛速度。本文算法相对于传统蚁群算法及文献[15]算法在收敛速度方面分别提高了88.5 %及62.5 %，大幅提高移动机器人搜索效率以及缩短了算法运行时间，验证了本文算法的优越性。

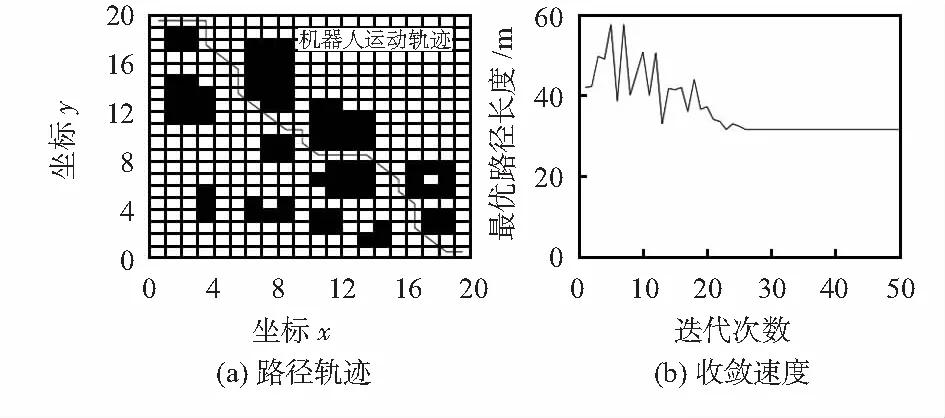
图3 传统蚁群算法路径规划

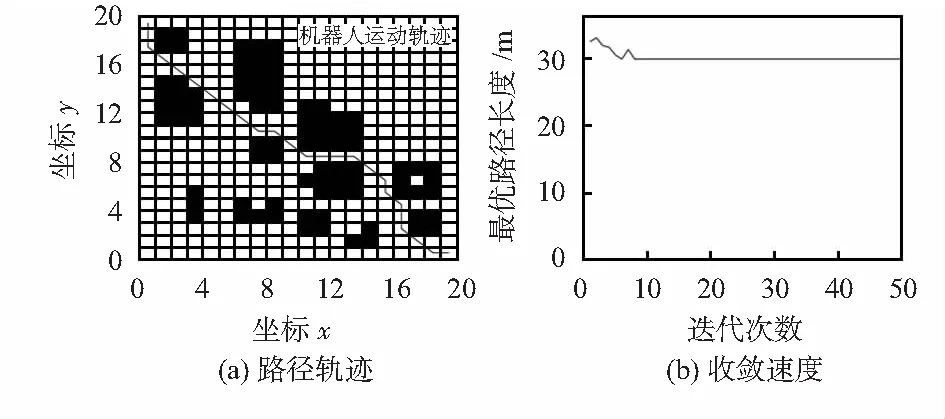
图4 文献[15]算法路径规划

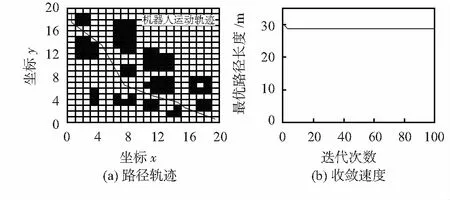
图5 本文算法路径规划

4 结 论

本文提出了改进变步长蚁群算法。通过对平滑机制的改进，进而实现对变步长的改进，扩大步长选择范围，优先选择步长更长的路径。在避开障碍物的条件下，对多次转角的位置用大步长路径代替，减少转折点，从而缩短移动机器人路径长度；同时，死锁问题是移动机器人利用蚁群算法进行路径规划遇到的常见问题。本文通过改进蚁群系统，通过启发式的搜索方式使得蚁群避免陷入局部最优，便于蚁群寻找全局最优解。对不同路径进行比较，加强最优路径信息素浓度，多个个体分布式的并行计算，提高路径被选择的概率。引入信息素惩罚函数，避免移动机器人陷入死锁或局部最优，大幅提高蚁群算法的运行效率。