基于双通道注意力网络的脑电图意图识别*

孙亚东，徐晓涛，章 军，陈 鹏

(1.安徽大学 电气工程与自动化学院，安徽 合肥 230601；2.安徽大学 互联网学院 农业生态大数据分析与应用技术国家地方联合工程研究中心，安徽 合肥 230601)

0 引 言

近年来，脑机接口(brain-computer interface，BCI)在学术界和工业界引起了广泛关注，它是一种使用脑电图(electroencephalography，EEG)信号使人能够与计算机或智能设备控制的人机交互技术[1]。EEG是一种获取与步行或站立等各种运动相对应的脑神经元电信号有效的方法，当受试者想象某些动作(例如抬腿)时，可以通过EEG信号分析这些动作，表示其意图[2]。

近年来，深度学习已成功地应用于图像分类和目标检测等领域。与传统算法相比，深度学习算法可以更加有效地学习EEG的潜在特征。为了提高分类性能，Schirrmeister R T等人使用卷积神经网络(convolutional neural network,CNN)对EEG信号进行识别[3]。考虑到EEG信号为一维时间序列数据，也可以在基于EEG信号的意图识别中采用了循环神经网络(recurrent neural network，RNN)，所以,Zhang D等人提出了一个7层RNN模型进行识别[4]。

综上所述，本文提出一种融合双通道模型—深度注意力卷积长短时期记忆(deep attention convolutional long short term memory，DACLSTM)网络，融合了CNN和RNN的优势，可以对EEG信号有效地提取特征。特别地，由于EEG数据的不同特征在分类中起着不同的作用，受注意力(attention)网络的启发[5]，可利用注意力机制关注重要的特征。使用正交矩阵进行参数调节，较传统的超参数调整方法可节省98.4 %的时间;所提出的框架通过Eegmmidb的公共数据集进行了广泛评估，实验结果表明该框架明显优于现有技术。

1 深度意图识别网络

本文提出的融合方法包含以下部分：深度特征学习，注意力机制和意图识别。

1.1 深度特征学习

图1说明DACLSTM网络的所涉及的不同流程。

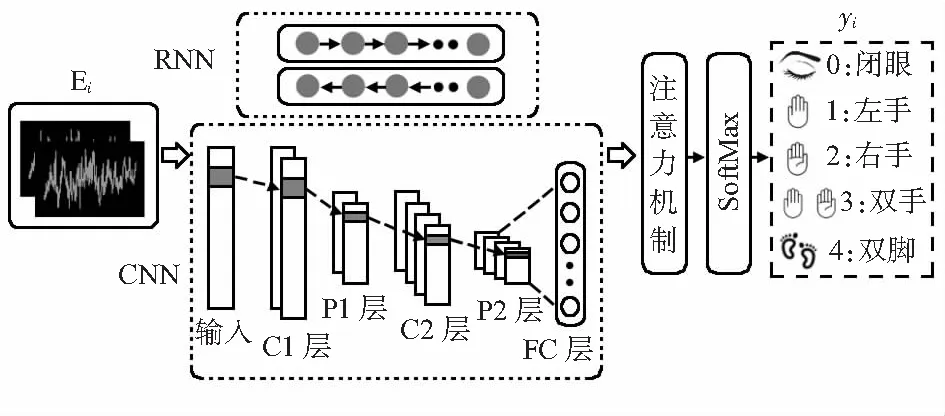
图1 DACLSTM网络结构

首先需要学习用户的意图信号表示形式，该信号是一维向量(在一个时间点中收集)。将单个EEG信号表示为Ei∈K，其中K是EEG信号的维数(文中K= 64)，yi∈R并表示样本Ei的类别。然后将Ei分别加入到给定的RNN和CNN结构，用于并行的时间和空间特征学习。

1)RNN特征学习

采用RNN的功能可以提取时序数据中的时间特征。本文使用的是一种特定的RNN，即双向长短时期记忆(bidirectional LSTM，BLSTM)。

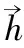
(1)

(2)

(3)

式中W为权重矩阵，b为偏置向量，o为BLSTM的输出。

2)CNN特征学习

CNN结构由三部分组成：卷积层，池化层和全连接层。由图1中CNN部分可知，按以下顺序堆叠设计的CNN：输入层，卷积层1(C1)，池化层1(P1)，卷积层2(C2)，池化层2(P2)，全连接(FC)层。

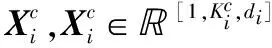
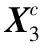
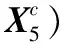
1.2 注意力机制

H=[h1,h2,…，hn]

(4)

在获得样本数据的BLSTM和CNN特征表达后，利用注意力机制获得融合特征映射。注意力机制的结构如图2所示。注意力的计算方式描述如下

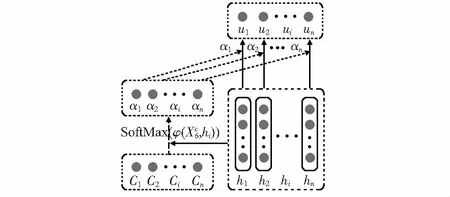
图2 注意力机制模型结构

(5)

(6)

(7)

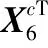
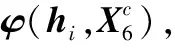
1.3 意图识别

在深度学习网络中，SoftMax函数比其他激活函数更适合用于多分类问题。SoftMax函数的输出概率计算如下

p′=SoftMax(Ws·umap+bs)

(8)

损失函数使用交叉熵，并通过Adam Optimizer算法[7]进行优化。

2 算例分析

2.1 数据集介绍

本文使用由Eegmmidb提供的公共EEG数据集，该数据集使用BCI 2000系统对不同运动或者图像任务的对象进行操作，并记录64个通道EEG数据[8]。本文使用了28,000个EEG信号，每个样本都是64个元素的一维向量。数据集被随机分为两部分：其中,70 %的样本作为训练集，剩余30 %样本用作测试集，将标签转换为独热(one-hot)编码进行分类。选择的EEG信号分为五类，每种意图对应的标签如图1中意图识别部分所示。

2.2 正交矩阵实验设计

尽管深度学习算法可以在许多领域取得良好的性能，但是调整超参数非常耗时，并且依赖于个人的经验。本文采用正交矩阵(orthogonal array，OA)实验设计[9]来选择超参数，该方法比传统的超参数调节方法要快得多。

OA是一种系统的统计方法，其原理是比较由自变量的不同组合产生的因变量。在此方法中，自变量称为“因子”，因子的不同值称为“水平”。例如，如果某方案具有3个因子，并且每个因子有3个水平，这些水平由27个结点的多维数据表示(每个结点代表一个超参数组合)，则OA仅选择9个代表性参数组合进行优化选择。

为了获得最佳的识别精度，本文采用OA实验方法来优化超参数，并选择适用于本文的5个常见的超参数，包括λ(2—范数的系数)，lr(学习率)，Ki(BLSTM隐藏神经元大小)，An注意力大小(即向量v在式(6)中的大小)和N(表示批数量。训练集和测试集的大小取决于nbs，因为总数据集是固定的，例如，如果nbs等于1，则将有14 000个训练数据集和14 000个测试数据集。如果nbs等于3，则有21 000个训练数据集和7 000个测试数据集)，如表1所示。由于本次OA实验包含了5个因子和4个水平，因此由标准正交实验表可知，应进行16个实验优化超参数。

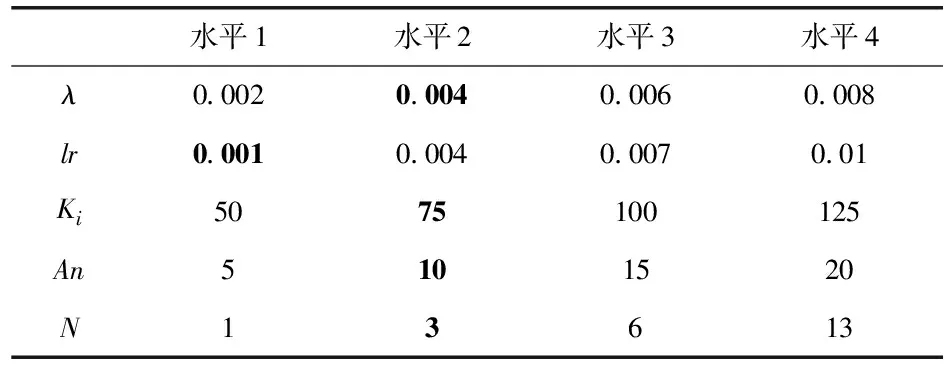
表1 因子和水平

超参数的组合以及实验结果的范围分析，如表2所示。通过OA实验调节可得最佳λ，lr，Ki，An，N参数分别是0.004，0.001，75，10，3。用穷举法选择5个因子和4个水平的参数需要1 024=45个组合，而使用OA实验分析则只需要16种组合，说明节省了(1-16/1 024)=98.4 %的时间。本文选择了OA实验调节后的最佳水平参数来训练模型，并获得99.34%的准确率。

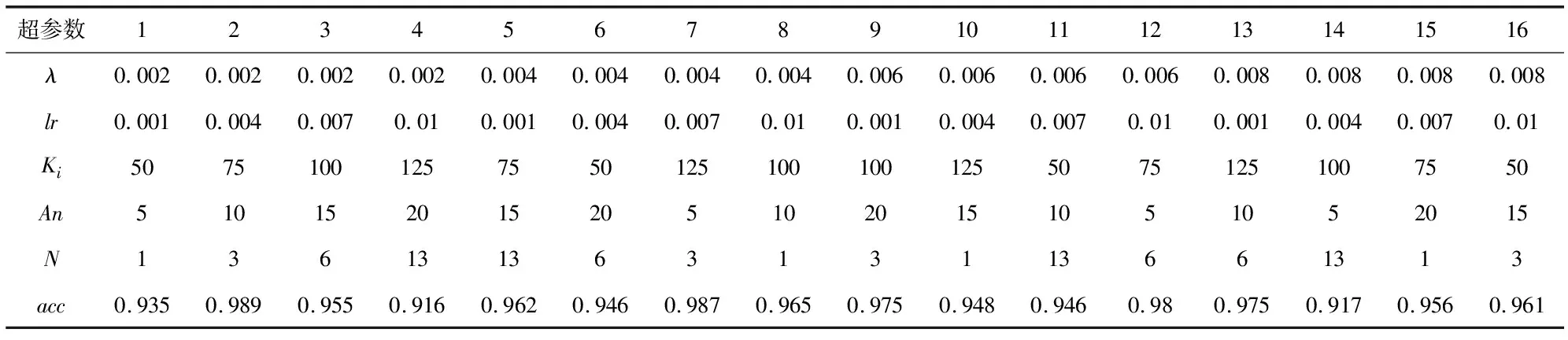
表2 OA实验因子分析

2.3 实验分析

为了验证所提出的融合模型实验的有效性，在基于TensorFlow的深度学习平台上实现该模型，并与单一的CNN和BLSTM模型在同一数据集进行对比实验。EEG数据的输入形式是一个三维的张量(?, 1, 64)，“?”表示训练时每批次输入样本的数量，即nbs。

在DACLSTM模型中，CNN通道的数据经过1.1节分析可知输出结果为(?,64)，BLSTM通道的数据经过一个输出维度为50的BLSTM单元，取其隐藏层的输出，结果为一个(?,64,50)的张量。将2个通道张量通过Attention层进行融合，形状变为(?,1,50)，即为EEG数据的融合特征表达，再通过Dropout层(防止过拟合)，最后由FC层激活输出，输出的维度为1，激活函数为SoftMax。

CNN模型和BLSTM模型分别与DACLSTM模型去掉Attention层的左、右通道类似。图3表示各模型的ROC曲线，横坐标是假阳率(分到正例中真实的负例占所有负例的比率)的对数，纵坐标为真阳率(分到正例中真实的正例占所有正例的比率)。可以看出图3(a)中DACLSTM模型比图3(b)和图3(c)更靠拢(0,1)点，偏离45°对角线，灵敏度、特异性更大，效果更好。

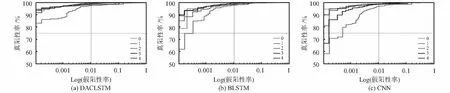
图3 各模型的ROC曲线

2.4 与其他方法的性能比较

表3为所提出的模型与现有方法和基准方法的性能比较。基准方法中提及算法如下：KNN表示k最近邻，SVM表示支持向量机，RF表示随机森林，LDA表示线性判别分析，各超参数为：KNN(k=3)，SVM(c=1)，RF(n=300)，LDA(tol=10-4)和AdaBoost(n=500，lr=0.3)。综上所述，所提出的模型优于包括现有方法和基准方法在内的所有技术，并将识别准确率提高了1.06 %。

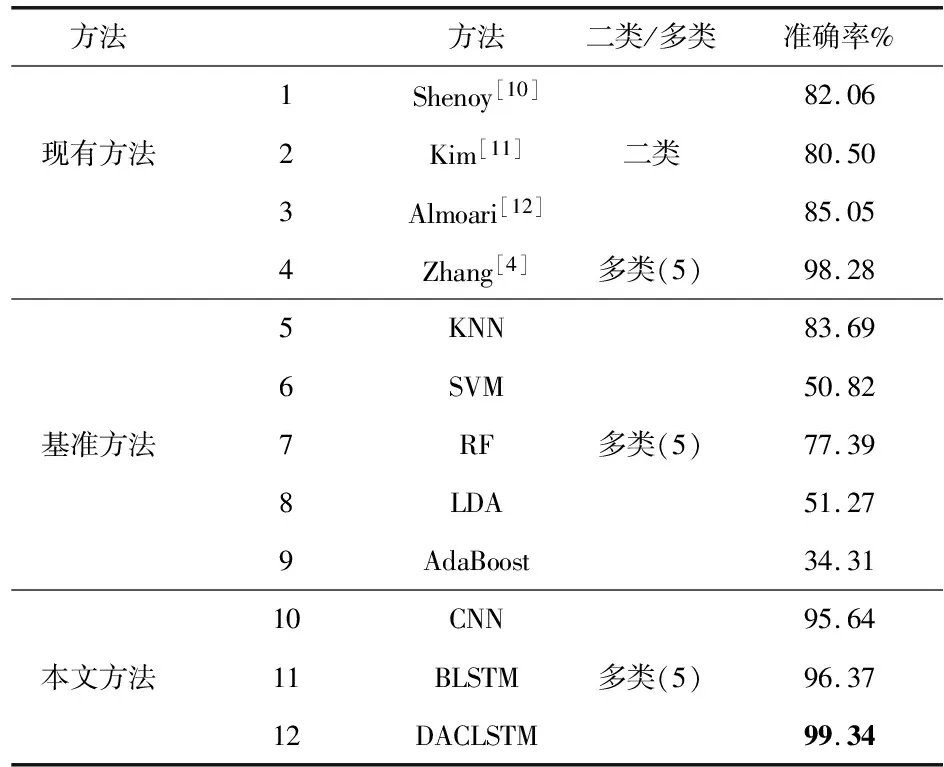
表3 与现有方法与基准方法的性能比较

3 结 论

本文提出了一种融合深度网络，即DACLSTM，建立了基于EEG信号的意图识别系统。在实验结果方面，DACLSTM模型实现了99.34 %的高识别率，证明模型意图识别有效。此外，本文研究了有注意力和无注意力的CNN和BLSTM模型，以发现注意力模型的意义。另外使用OA实验调节参数，可节省98.4 %的参数调节时间。为了使比较更加直观，本文将提出的方法与同一数据集上的现有方法和基准方法进行了比较，均优于以上方法。