基于天牛须蜂群PID算法的闪蒸罐压力控制*

程宗政，施一萍，刘 瑾，吕晨悦，张金立

(上海工程技术大学 电子电气工程学院，上海 201600)

0 引 言

闪蒸罐是复杂工业生产中的重要化工单元，一直以来都被广泛应用于加氢裂化和硫化尾气回收的过程[1]。但由于其属于非线性、大滞后的复杂控制系统，传统比例—积分—微分(proportional-integral-differential,PID)算法很难满足控制要求。因此,越来越多的智能算法被应用到PID参数的整定上。金滔等人[2]提出利用改进粒子群优化(particle swarm optimization，PSO)算法整定PID参数，但存在易陷入局部最优的问题。周勇等人[3]提出改进遗传PID算法的控制策略，依然都存在算法收敛速度较慢，压力控制实时性不够的问题。鉴于此，本文提出天牛须蜂群PID算法，大大提高了算法的收敛速度和全局寻优精度，在此基础上设计压力控制器对闪蒸罐的压力进行控制，为闪蒸罐压力控制提供了一种全新策略。

1 天牛须人工蜂群算法

1.1 人工蜂群算法

人工蜂群(artificial bee colony,ABC)算法是由Karaboga根据蜜蜂群体不同角色相互协作进行觅食的原理提出的新型智能寻优算法[4]，蜂群模型由三种蜜蜂组成：雇佣蜂、旁观蜂和侦察蜂[5,6]。整个过程是利用雇佣蜂搜索空间并记录食物源的位置，然后将信息传递给旁观蜂。根据雇佣蜜蜂传递的信息，旁观蜂选择食物源。若一个食物源耗尽，雇佣蜂转变为侦察蜂，并重新开始搜索。

雇佣蜜蜂和旁观者蜜蜂根据式(1)搜索食物来源

xij(n)=xij(n-1)+φij[xij(n-1)-xkj(n-1)]

(1)

式中j和i为随机数;j为第i个食物源的一个维度;xij(n-1)和xij(n)为新旧食物源的位置;φij为介于-1和1之间的随机数;k为一个随机索引，并且k≠i。

可能性值由式(2)计算

(2)

式中Pi为旁观者蜜蜂选择第i个食物源的可能性值，FoodNumber为可行解数量，f(i)为第i个食物源的目标函数值。

trail是可行解xi(第i个食物源位置)未改进的次数,limit表示它的最大次数。当第i个食物源trail>limit时，证明其已陷入局部最优解。因此，雇佣蜂放弃位置，成为侦察蜂，根据式(3)在全局范围内寻找新的食物源

Xi(0)=Xlb+(Xub-Xlb)rand(0,1)

(3)

式中Xlb为可行解的下界，Xub为可行解的上界。

1.2 天牛须蜂群算法

在常规ABC算法中，雇佣蜂搜索新的食物源时，是从现有食物源中随机选择食物源，这将导致算法的收敛速度降低。为了解决进化方向随机、收敛速度慢的问题，引入了天牛须搜索(beetle antennae search,BAS)算法[7，8]对ABC算法进行改进。

在BAS算法中，天牛能通过比较左右触角所接收到的气味强度，选择强侧作为下一个移动方向，这种特性提高了搜索食物源的能力。由于食物源的搜索更具方向性，算法的收敛性也将得到显著改善。

首先，选择食物源的一维作为进化的方向，用以下公式来描述方向

(4)

式中 rand(·)为一个随机函数，k为食物源的维数之一。然后，模拟左右两侧的搜索行为，如下所示

(5)

式中xir(n)为位于右侧的位置，xil(n)为位于左侧的位置。l为根据搜索能力确定的食物源一维中触角的搜索长度。

其次，比较左右两侧目标函数值的大小，得出检测行为，使用以下方程式来描述检测过程

(6)

式中δt为搜索的步长，随着搜索周期的增加而减小。符号sign(·)为比较左右两侧目标函数值大小的函数。如果f(xir)大于f(xil)，则符号sign(·)取-1；如果f(xir)小于f(xil)，则符号sign(·)取1。

结合以上两个方面，在寻找雇佣蜂的新食物源之前，确保在每次搜索之前确定搜索方向，而不是随机选择。

2 BABC-PID控制器设计

针对工业生产中闪蒸罐压力控制难题，引入了天牛须蜂群算法设计了一种BABC-PID压力控制器，利用改进的天牛须蜂群算法优化PID控制器参数。BABC算法将求解最优PID参数问题变为求解蜂群的最优蜜源问题[9，10]。基于BABC-PID闪蒸罐压力控制器如图1所示。

图1 BABC-PID压力控制器

选取ITAE作为适应度函数，并在式中加入控制量平方，如下式所示

(7)

式中Q1，Q2为系数；F为适应度。若e(t)=r(t)-y(t)<0，则启用超调惩罚功能，F如下式所示

(8)

式中Q3为系数，令Q1=0.999，Q2=0.001，Q3=100。

BABC算法对PID参数整定流程如下：1)确立PID控制器参数的解向量，并通过BAS算法确定雇佣峰的搜索方向;2)计算解向量的适应度值，得到最小适应度值的最优解参数;3)设置雇佣蜂未更新次数trail为0;4)根据式(1)寻优新解,若新解适应度未能减小，则将适应度值减小并将trail加1;5)根据式(2)计算雇佣蜂解向量的适应度值比例，比例越大越容易被旁观蜂选择,旁观蜂则根据贪心法则确定更优解，并根据步骤(4)的方法确定雇佣蜂未更新次数trail;6)计算本次迭代的最小适应度值，如果优于之前的最小适应度值，则将其赋值给全局最小适应度值，并将其对应的最优解赋值给全局最优解;7)若trail>limit，则放弃当前蜜源。同时将该蜜源对应的雇佣蜂改为侦察蜂，按照式(3)重新计算新的蜜源来替代原本的蜜源xi;8)若迭代结束则输出最优PID参数，否则跳至步骤(4)。

3 仿真实验

3.1 BABC算法性能测试

选取Sphere,Rosenbrock,Rastrigin,Griewark,Achley共5个基准函数，分别表示为f1，f2，f3，f4，f5。利用其对BABC算法、ABC算法以及PSO算法进行测试，基准函数维数为50[11]，参数限制设定为50，种群设置为100，最大迭代次数为5 000，经过100次运行获得的结果如下表1所示。无论是单峰基准函数还是多峰基准函数，运行结果都表明BABC算法在求解精度和收敛速度方面都明显优于粒子群优化(particle swarm optimization,PSO)算法和常规ABC算法。

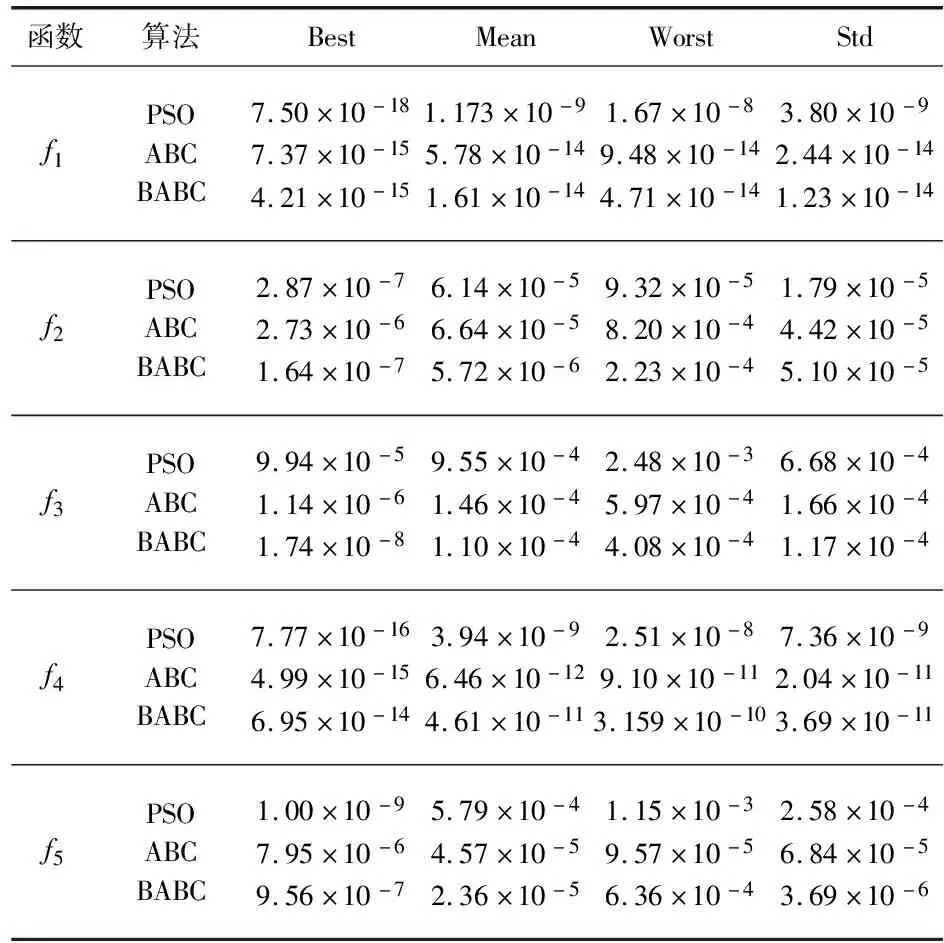
表1 PSO,ABC和BABC性能测试表

3.2 压力控制仿真实验

为了更好地了解BABC算法的实际寻优效果，使用MATLAB编程m文件对比PSO、ABC和BABC算法的适应度变化情况。并且结合文献[3]中闪蒸罐压力系统的数学模型G(s)=9e-10s/(100s+1)进行阶跃响应仿真实验。种群规模设为30，最大迭代次数为50，各算法适应度变化如图2所示。PSO算法和ABC算法趋于稳定的迭代次数分别为35次和17次，而BABC算法趋于稳定的迭代次数仅为8次，迭代次数明显减少。BABC算法提高了其在PID参数整定时的动态响应特性，同时BABC算法具有更好的收敛性，所得结果同用基准函数测试的性能结果一致。

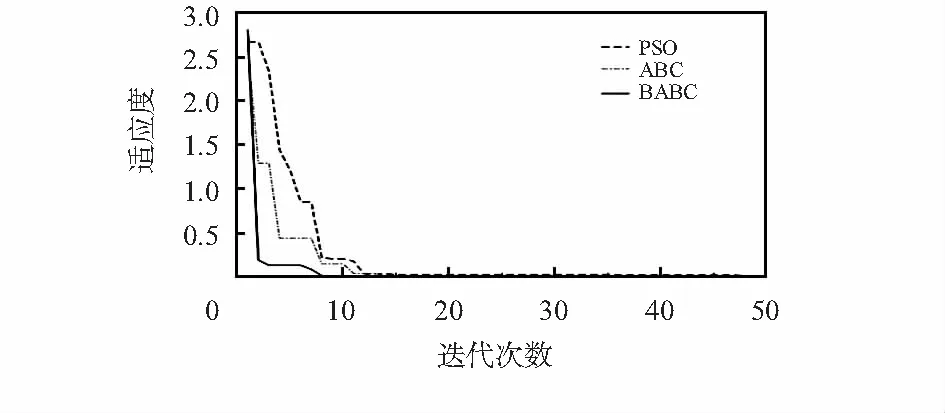
图2 PSO,ABC和BABC算法适应度变化曲线

图3为BABC-PID,ABC-PID以及PSO-PID三种算法对闪蒸罐在两种压力要求下的控制性能情况，阶跃响应曲线的各项参数如表2所示。在两种工况下，PSO-PID算法的超调量都较小，但自身的调整时间过长，不能满足闪蒸罐压力调节的实时性要求。相比于PSO-PID算法，ABC-PID算法在调整时间和快速性上有很大的提升，但缺点是存在一定的超调量，给闪蒸罐罐体的承压和物料输送造成负担。而BABC-PID算法在反应时间几乎不变的情况下，超调量减小到了0.1 %，调整时间缩短了31 s，大大提高了闪蒸罐压力控制的实时性和稳定性。

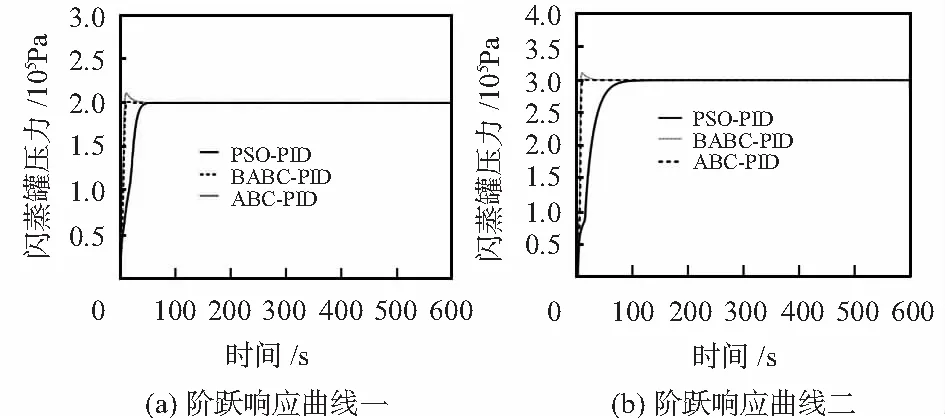
图3 PSO,ABC和BABC算法的阶跃响应曲线

表2 闪蒸罐压力系统阶跃响应参数指标

3.3 闪蒸罐压力实验

本文通过MATLAB对BABC-PID算法在闪蒸罐数学模型上进行了仿真实验，为进一步了解算法的应用效果，借助SMPT-1000高级过程控制实验设备和西门子的SIMATIC PCS7软件设计了闪蒸罐的压力控制实验。本文分别用传统PID算法和BABC-PID算法对混合物料进入闪蒸罐时的压力进行控制，实验结果如图4所示。

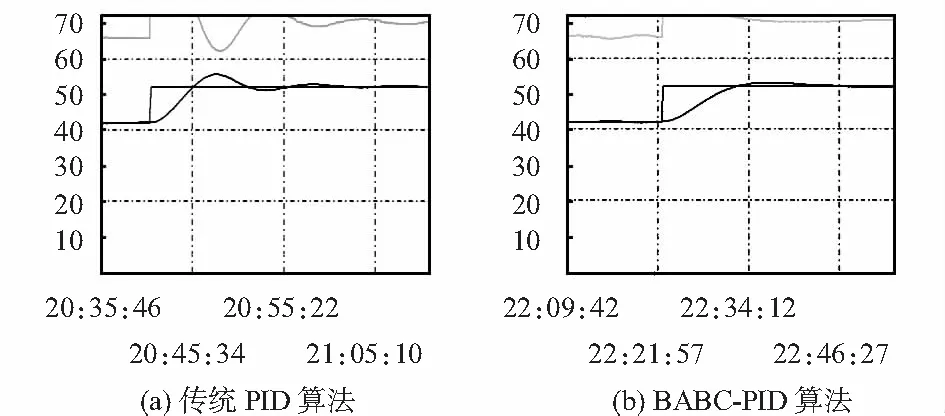
图4 二种算法的压力控制效果

图4(a)中给出压力阶跃信号后，传统PID算法对闪蒸罐压力的调整时间为1 400 s左右，超调量超过了30 %。而图4(b)的BABC-PID算法对闪蒸罐压力的调整时间仅为1 000 s左右，并大大降低了超调量，使得闪蒸压力控制的实时性和安全性得到提高。通过闪蒸罐的压力实验和仿真实验表明BABC-PID算法的动静态性能都得到很大程度的提高。

4 结 论

本文提出一种BABC-PID算法对闪蒸罐压力系统进行控制。闪蒸罐压力控制的调整时间的降低改进了压力控制的实时性，同时超调的降低减少闪蒸罐在闪蒸分离时承受的负担，极大地提高了闪蒸罐的稳定性和动态特性，对闪蒸罐的分离提纯具有很重要的意义。