动态因素下时序称重模型的建立

史柏迪， 庄曙东， 陈 威， 陈天翔， 朱楠楠

(1. 河海大学机电工程学院，江苏 常州 213022;2. 南京航空航天大学 江苏省精密与微细制造技术重点实验室，江苏 南京 210016)

0 引 言

在日益增长的物流需求和人工劳动力缺口矛盾面前[1-2]，自动化动态称重技术是物流业发展的必然之路。动态物流秤在货物运输的过程中对货物质量进行了测量，减少了人工成本，化简了物流流程。其测量大多依赖电阻应变型压力传感器，作为典型的机电复合系统传动过程中，压力传感器会受到各类干扰信号，例如秤体自身传动电机产生的振动干扰[3]、货物在传动过程中的振动干扰[4]及环境因素(气温、湿度、空气对流)等，作为典型的多元非线性过程[5]具有复杂性与无序性，压力信号包含静态载荷[6]、动态载荷[7]以及动态时序噪声，因频段信号的重叠，仅凭借滤波处理无法获取精确的压力信号。为有效分析各对测量精度的影响，设计了三因素两水平的正交试验，以此结果作为数据集建立Xgboost[8]模型进行特征增益分析。

动态补偿系统[9]为目前一种可行的解决方案，国内外已经有了诸多成果。刘元坤[3]基于高斯过程建立了轮廓误差分布概率函数，在加工中实现了轮廓测量误差的柔性化补偿。Irwansyah[8]基于机器学习中最近邻算法实现了声纳噪音信号的聚类，通过频率筛选有效提取有效信号；Hussain Muntazir[9]使用支持向量机算法建立一种 Lipschitz系统的抗饱和补偿模型。此外神经网络算法因其强大的多元非线性拟合能力，在动态称重系统[10-12]中也有着广泛的使用。但上述模型均以数据为导向，使用特定算法对采样点内信号进行处理，输出补偿值。忽略动态测量在时序上的连续性，将时段内的采样点与采样点内的信号作为整个输入源。本论文使用的神经网络模型在LSTM模型门式结构之中加入全连接层，一方面避免了循环神经网络“长期依赖问题”在长时段下有效训练，此外通过在横向门式结构中增加全连接层增强了模型非线性拟合能力，提高了预测精度。本论文分析对象为某公司的TW155型动态秤，目前在国内多家物流以及航空公司动态称重计费系统中有着广泛使用，分析对象具有普遍性。

1 试验设计与数据处理

1.1 正交试验设计

使用STMicroelectronics公司生产的LIS3DH型振动传感器采集秤体的三轴加速度信号。其采样频率为 [10，367] Hz，压力传感器为 MettLer-Toledo公司的0745A型，其采样频率与振动传感器一致。测试货物质量M依次为 9.876 kg、19.761 kg；运行速度V为 40 m/min、60 m/min；采样频率H为 100 Hz以及200 Hz，MAE为补偿绝对误差。表1为3因素2水平标准正交组合表。

表1 正交试验表及补偿误差

为避免随机误差各组序列进行100次测量，表1中W为对采样平稳段内信号基于式(1)处理的结果

式中：N——每组组合下测量次数；

t——其样本索引；

s——上秤区间所采集数据的数量；

i——其索引。

s与传送带速，传感器采样频率相关，因此各类因素组合下各不相同，n为四组压力传感器采集到的压力信号，其安装位置与试验环境图1。

图1(a)为放置20 kg货物时测试环境图，TW155型动态秤放置为中间级，每轮皮带正反转货物上秤时对加速与压力传感器信号进行采集，各传感器放置位置图1(b)。最终按表1因素组合进行试验，共计获取了400组样本，各模型训练集与测试集从表1各因素组合中分层随机抽样取得，各模型最优超参数使用训练集样本基于五折交叉验证确定。

图1 测试工况

1.2 岭回归补偿模型

在机器学习算法中常使用岭回归[13]来度量问题的复杂度，在本问题中可得式(2)优化目标。

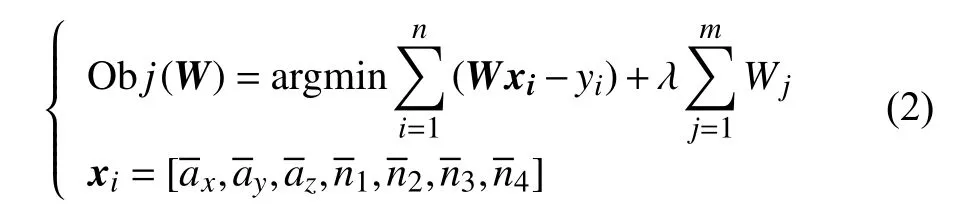
式中：W——待求回归系数矩阵；

λ——岭回归系数；

n——训练集样本数目；

m——自变量数目；

y——真实质量；

xi——货物上秤区间内各信号均值组成的向量；

Wj——第j项自变量的系数项。

基于凸优化原理，在岭回归系数确定的情况下使用最小二乘法一定有最优解式(3)。

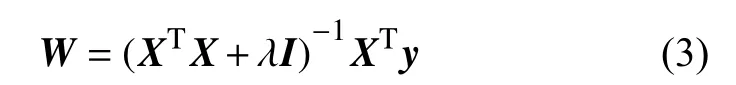
式中：I——单位对角矩阵；

X——样本矩阵；

λ在区间(0，1)内设置步长0.01在五折交叉验证下基于网格化搜索原则确定。图2为λ设置0.14最佳情况下，测试集拟合状况。

图2 测试集拟合绝对损失

图中，为使增强可对比性，直接给出多元线性回归补偿损失；可知采用岭回归补偿相对线性回归损失显著降低，通过引入岭回归系数虽放弃了对于已知数据的无偏性与拟合精度，但对于未知样本具有更好的泛化性，拥有更好的补偿精度。岭回归与线性回归模型最终平均损失依次为0.317 kg与0.671 kg，较平均采样法提升明显。通过python基于式 (3)求解出各项系数依次为 12.4132、–49.9237、–16.1591、–36.6708、45.2027、33.1397、36.2274。

2 Xgboost模型与特征分析

2.1 Xgboost回归原理

在章节1中基于岭回归建立了补偿模型，但其本质依旧为线性回归类模型，无法有效对多元非线性系统进行精确补偿。Xgboost作为集成学习类算法，在T轮迭代中通过集成回归树f优化上轮残差使模型不断逼近真实值，此外通过引入正则化项目Ω(f)有效约束各回归树的深度以及叶子节点分裂数目有效避免了过拟合，目前Xgboost在各类数据分析类竞赛Kaggle、天池等有着广泛使用，本模型在python语言环境使用 scikit-learn[14]以及 Xgboost工具箱实现。与岭回归相似，其优化目标由目标函数与正则化项组成可表示为式(4)：

式中：θ——Xgboost待修正超参数；

n——训练集样本数目；

l——均方误差，其有两个输入：样本真实值y与模型输出；

g，h——模型的一阶与二阶损失梯度函数；

C(f)——正则化函数；

K——集成回归树的数目；

T——叶子节点数；

γ——正则化系数；

w——叶子节点权重；

x——输入信号矩阵，其中a、n为加速度与压

力传感器信号组成的向量，各自包含采样区

间内的s个数据点。

Xgboost算法在每轮迭代中各回归树直接作用优化残差，基于泰勒公式可以将第t轮目标函数Objt二阶展开为式(5)：

其中gi、hi为基于式(5)求得样本i的特征的梯度与偏置；结合式(6)减去引入该叶子节点的代价γ即可得各特征对应叶子节点所占输出权重。

2.2 基于Xgboost的特征分析与测量补偿

基于式(4)～ (7)对表1数据进行处理可得图3形式的压力传感器与加速度特征权重分布规律。

图3 Xgboost特征分析

图中，x轴坐标为各特征对最终输出值的F检验结果为无纲量参数。y轴为各特征；最终补偿输出测量结果的精度，主要依赖于压力传感器信号，其次因带面的不平整，运动中z轴加速度对最终补偿结果有较大影响。图4为该模型测试集样本损失。

图4 Xgboost特征分析

图中，虽存在部分样本补偿误差大于岭回归，但总体误差量显著降低，最终平均损失为0.219 kg。

3 长短期记忆神经网络

3.1 输入信号时序化处理

上述岭回归与Xgboost模型，本质上依旧只是一种监督回归模型通过输入特征输出补偿值对比真实观测量，基于误差修正模型超参数，从而不断提高模型精度。但上叙模型特征输入时没有考虑采样时段内压力与传感器信号在时间序列上的连续性。当时间序列样本长度为n，回顾步长为k，即t（k≤t≤n–k）时刻的状态，依赖区间 [t–k,t）时刻的状态，且直接区间（t,t+k]时刻状态产生影响。在LSTM算法之下可得时序递推关系式(8)：

式中：LSTM——网络正向传播处理，其输入为k个采样信号点x；

FM——经LSTM处理后取得的预测值。

步长k决定使用多少个先前状态来推导下一时刻的状态,在一定范围内k越大，模型越精确。本模型根据采样频率 100，200 Hz，设置为 3、5。

3.2 改进LSTM模型的建立

LSTM结构中通过遗忘门、输入门和输出门来控制细胞状态。门结构中通过sigmoid层对数据进行点乘完成数据特征的添加与删除。有效解决在长时段情况下循环神经网络的在上述产生的长期依赖性问题。设当前时间序列为t；数据输入为x；预测输出为h；c为记忆单元可得图5网络结构。

图5 LSTM神经网络结构

图中，σ为 sigmoid激活函数；[ht–1,xt]为上一轮预测结果ht–1与本轮输入参数xt的复合矩阵；xt为第t时刻输入参数；Wf为遗忘门权重矩阵；Wi为当前输入门权重矩阵；Wc为输出权重矩阵；Wo当前状态控制矩阵。遗忘、输入、控制与输出门其数值表达可表达为：

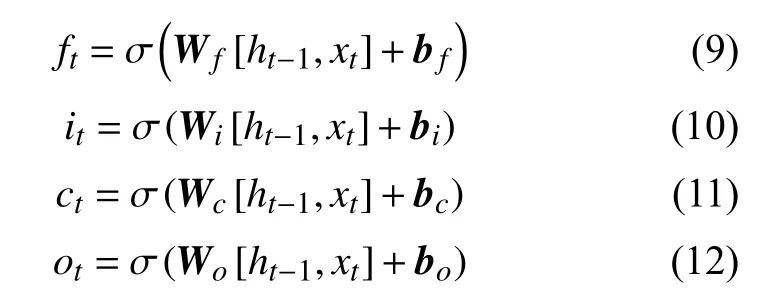
其中其余各项参数均已说明。bf、bi、bc、bo为遗忘、输入、控制与输出门的偏置向量。

通过将式(10)～ (13)中各项门的权重矩阵W设置为0、1通过点乘操作可有效对输入参数添加与删除特征且sigmoid函数输出值域为(0,1)，任意门的状态均为于半开半闭,可以有效控制其算法复杂度。LSTM在t时刻的最终输出由输出门与单元状态共同决定式(13)。

结合式(8)～ (13)为LSTM神经网络在处理时间序列任务时前向传播过程结合图5可知在每个时段模型的输出不仅为本轮预测值且将预测值与该时间段内记忆单元作为下时刻网络的输入。

易知在n个采样点中，若步长为k，LSTM网络会产生n–k个输出，为增强模型非线性处理能力，对其输出堆叠经典BP神经网络中全连接层结构。该方法浙大学者张剑[13]在其博士论文中也有所使用，对传感器信号使用了滤波与自适应处理来降低噪度随后将采样点内有效信号输入BP模型，高维数据矩阵交由网络加权输出得出最终预测值，预测精度较各类传统模型提升明显。本模型将BP神经网络的输入设置为已由LSTM神经网络输出预测值，其规格仅为长度为n-k的行向量。网络包含三层结构，输入层、全连接层、输出层，其中数据的多元非线性关系交由全连接层进行映射，输入层与输出层仅包含数据的归一标准化与反归一化处理。设置BP神经网络隐藏层神经元数目(m)为64简写其为u；LSTM神经网络使用tanh激活函数，基于kaiminghe[14]初始化神经网络为避免过拟合设置dropout系数为0.5，图6为本模型简图。

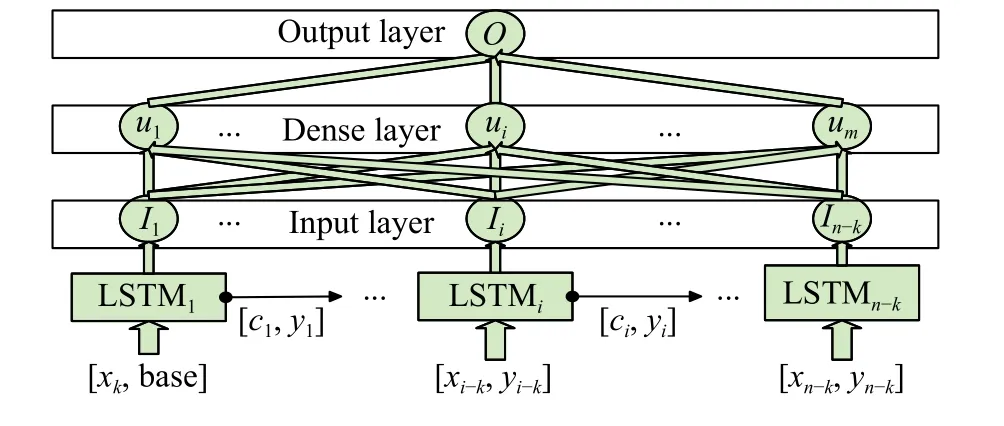
图6 改进的LSTM结构

图中，LSTM神经网络其详细内置结构为图5，其前向传播即为式(9)～ (12)；cell为隐层神经神经元，i为其序列索引，m为神经元数目，X为包含k列x形式如式(3)的矩阵；O（mg）为最终输出质量。

本模型基于pytorch库进行构建，因为其动态图的特征，在本堆叠模型之下依旧可以快速求得误差反向传播时各神经元的误差梯度进行超参数修正。使用RMSprop算法优化器自适应学习率，迭代次数为500，采用5折交叉验证处理，图7为模型训练训练时，训练集与验证集均方误差波动。

图7 LSTM-BP训练误差波动

图中,验证集损失每100次跌倒进行验证，当验证集损失大于上轮发生过拟合现象时，停止训练。易知随着当设置迭代次数为500时，训练集与验证集误差同步下降，学习效果良好。最终迭代终止时，训练集误差为 0.147 kg，验证集损失为 0.164 kg。

最终80个测试集样本损失如图8。

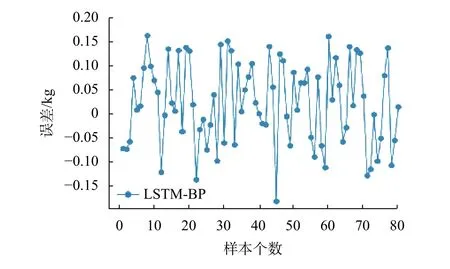
图8 LSTM-BP补偿损失

图中所有样本误差均被约束在[–0.2,0.2]kg之间，最终补偿平均损失为0.142 kg，误差最小。结合图2与图4，误差波动较小，且测试集样本从表 1四种因素中均匀抽取，有理由相信，LSTM-BP模型在各类工况(采样频率、速度、货物质量等)有着更好的适应能力进行可进行更为精确的动态补偿。本模型训练环境为普通家用计算机配置如下：i7 9750H，RAM 16G，GPU GTX2060，使用 cuda进行加速运算，最终耗时 3415.13 s，对比岭回归与 Xgboost可得表2结论。

表2 算法对比

表中，Ridge作为线性回归类算法其训练耗时大多用于交叉验证下寻找最优超参数，其运算时间复杂度大致可以忽略不计，因其有明确数学表达形式可以直接编单片机等嵌入式开发设备。Xgboost算法，其训练耗时与Ridge一致用于确认极限回归树模型最佳参数(迭代次数、最大叶子节点分裂次数、正则化系数等)。LSTM-BP模型作为一种时间序列模型，将各时间点输入特征作为一个独立输入，且将各时间点输出与网络状态进行横向连接，相对传统模型将区间内数据“打包”一体化处理，此改进的LSTM-BP更能挖掘货物上秤时间段内的非线性特征，输出更为精确的货物质量，但正如机器学习中“没有免费的午餐”[15]定律，因输入数据的时序化，LSTM层在各时间序列点中均需进行迭代参数,且其运行需要依赖特定编译环境，在单片机乃至FPGA等嵌入式开发设备中难以运行。

4 结束语

1）基于岭回归原理的补偿测量较线性回归模型提升显著，算法复杂度较低，可直接求解其线性数学表达式可直接写入单片机等设备中，但线性解释类模型在多特征称重补偿系统中精度难以得到保证。

2）使用Xgboost算法建立的补偿模型其精度较线性回归类模型提升明显，且基于树型结构可以分析其各叶子节点对特征的误差贡献率，提供一种基于F检验来量化误差的方式，在本模型中说明秤体x、z轴方向加速度对测量精度具有较大影响。

3）此改进的LSTM模型具有最好预测精度，本文虽说明其模型的训练与测试的可行性，但该补偿模型在目前市面上嵌入式开发板中受限于编译环境与配置难以进行。线性回归类模型，具有最好的可开发性与可解释性，但其精度直接受限于传感器精度，测量修正精度难以达到精度要求。

4）针对LSTM-BP神经网络难以训练时间较长的问题，可考虑在精度允许的范围之内，缩小输入特征数据规格；或缩小LSTM层与BP层尺寸。