MFA在相变性质研究中的伪解问题

陈 胜，卢俊邑

（电子科技大学物理学院 四川 成都 611731）

1 引言

随着铁电材料维度的降低，像纳米岛等低维结构材料表现出了一些非常奇妙的性质，从而引起了理论和实验研究的广泛兴趣，如关联有效场理论，格林函数理论，重整化群、蒙特卡罗模拟方法等。在纳米岛的相变机制下，我们研究可以采用考虑了横场分量的横场Ising模型，由于考虑了横场隧穿频率，其在一定程度上能够较好地与实验结果进行对照分析。

本文基于横场Ising模型，利用格林函数方法[1]的通常退耦合近似（MFA）研究正方晶格纳米岛的相变性质，并讨论了在初始自旋取向随机的特定情况下，相图和极化图非常规结果（如重入现象）以及产生机理。

2 模型和公式

我们考虑由两层正方晶格纳米岛的平面组成的三维正方结构纳米岛，每层平面的每个位置的原子分别占据一个Ising自旋，共计有9个自旋1/2的极性原子，见图1。

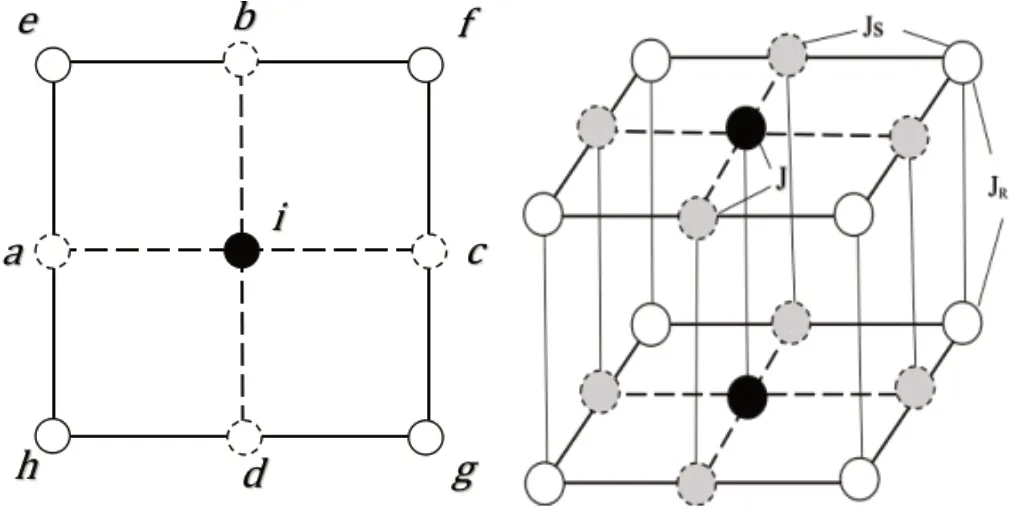
图1 正方晶格纳米岛的2D图（单层）与3D图（右）

由于此系统中，只有3种处于不同环境中的原子和3种不同格点之间交换相互作用常数Jij(＞0)，基于横场Ising模型的正方晶格铁电纳米岛的哈密顿量被表示为[2]：

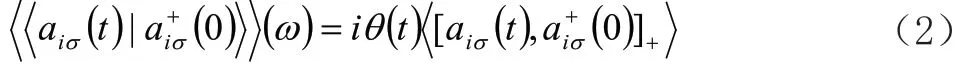
费米型格林函数的傅里叶分量满足运动学方程：

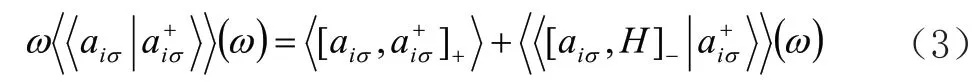
H是体系的哈密顿量，关联函数通过谱定理＜ai+σaiσ＞与费米型格林函数建立联系：

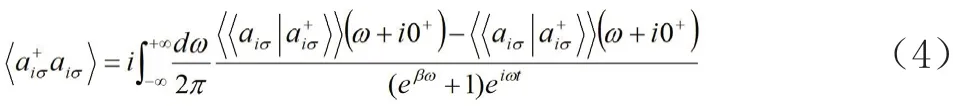
其中，β= 1/kBT，kB为玻尔兹曼常数，T是温度运动我方们程可[3-以4]：从TIM的哈密顿量推导出费米型格林函数的

为了能近似求解运动方程链，我们对上述方程组5～6采用通常解耦合近似处理：于是式5格林函数可以表示为：

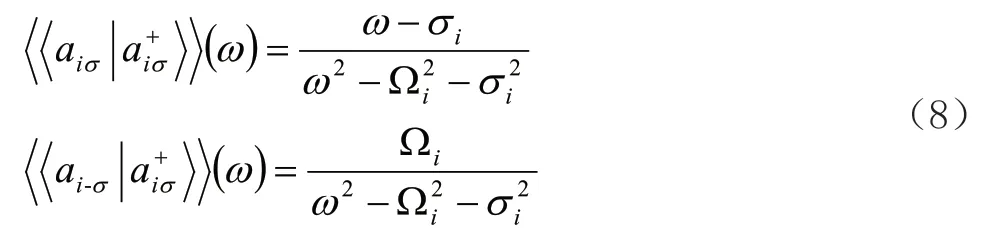
于是赝自旋的x和z分量可以写成：

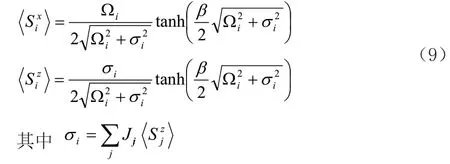
显然，在温度到达居里温度TC时，极化强度z分量等于0，可得到：

这就是通常平均场近似（MFA）的结果。由于处在相同环境中的原子极化强度相同，且只有处于3种不同环境中原子，于是我们总极化强度P可以用＜Si＞，＜Sa＞（或b、c、d），＜Se＞（或f、g、h）表示：

为了方便起见，引进无量纲温度JTktB/= 进行约化（约化后的居里温度?）。

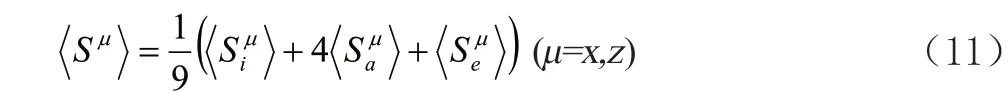
3 数值结果与讨论

3.1 相图

注意到在无横场时，即Ω/J=0.0时，在JS/J=1.0时，相变曲线（图2）为单调递增，表示出常规形状。增大横场到Ω/J=1.0时，发现相图曲线在JR/J=2.0处又开始生出一条点虚曲线，整个相变图形变成闭合曲线，并突出隆起。由于增大横场会降低纳米岛自发极化，使得铁电性减弱（极化强度降低，居里温度降低），因此Ω/J=1.0时的曲线必须在Ω/J=0.0曲线的下方，所以两组解（实线代表利用MFA解中值大的解tCH，虚线表示值小的解tCL）似乎都满足要求，这和T.Kaneyoshi[2]利用关联有效场理论得出的相图形状基本一致。横场与受温度决定的自发极矩相互竞争，在温度较低时，纳米岛处于基态。对于铁电材料，自旋完全同向，自发极矩很强，足以抗衡横场，此时自发极矩决定了纳米岛的自旋取向，但是随着温度的升高，由于分子热运动，无序性增强，自发极矩减弱，横场的存在使得纳米岛自旋取向发生改变，这就是阻挫效应。在JR/J=2.0～2.67范围内，具有两个转变温度，看似实现了纳米岛铁电相与顺电相之间的相互转变，即重入现象。

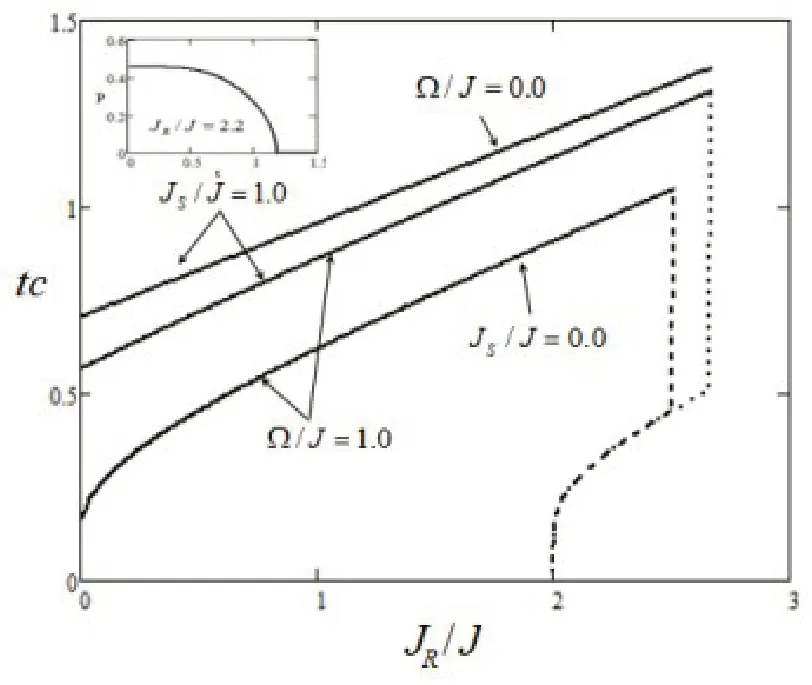
图2 Ω/J和JS/J分别改变时的tc~JR/J相图，小方框里为极化图。

进一步探究表面交换相互作用对相图重入现象的影响，发现随着JS/J的减小，仍然能够发生重入现象，但是相图的隆起程度变弱，tCH减小到2.518，但是tCL曲线（点虚线和短横虚线）并未发生明显改变，tCL曲线在JR/J=2.0到JR/J=2.518部分发生了重叠，JS/J=1.0的相变曲线完全包裹了JS/J=0.0的相图。JR/J=2.0～2.518范围内任取JR/J值，由于层间交换相互作用JR/J和横场Ω/J都是相同的，表面交换相互作用JS/J的不同会使得纳米岛铁电性不一致，必定使得居里温度不同。这里tCH符合该物理要求，但是tCL不符合该条件。通过研究JR/J=2.2，JS/J=1.0，Ω/J=1.0的情形下极化图P～t，我们可以发现在极化曲线为严格单调递减的，不产生任何奇怪的形状，即根本不存在两次相变。通过计算得知，此时居里温度tc=1.19。这和相变图中tCH结果完全一致。所以，我们有理由相信tCL是伪解，实际的相变曲线仅为一单调递增曲线，如实线所表示。

3.2 极化图

根据图2，我们知道纳米岛的“相变重入”现象主要在由于层间交换相互作用和横场。选择适当的JR/J和Ω/J，就有可能使得方程组9存在多解，也就可能存在着伪解。为了进一步探究MFA中伪解的产生原因，我们进一步T→0K时，正方晶格纳米岛的极化强度与横场的关系图P～Ω/J（见图3），和极化强度和层间交换相互作用的关系图P～JR/J（见图4）。

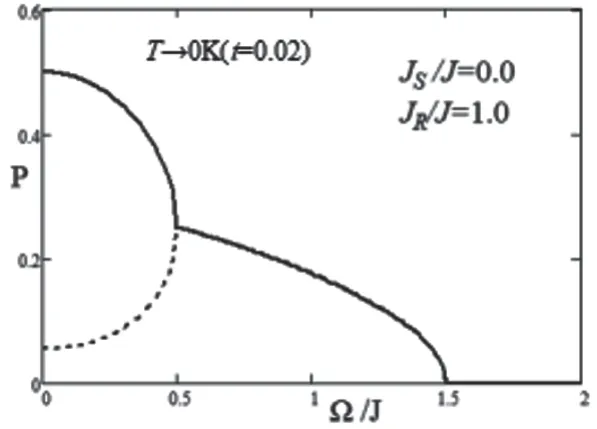
图3 JS/J＜＜1时，T→0K的极化强度P随横场Ω/J的依赖关系图

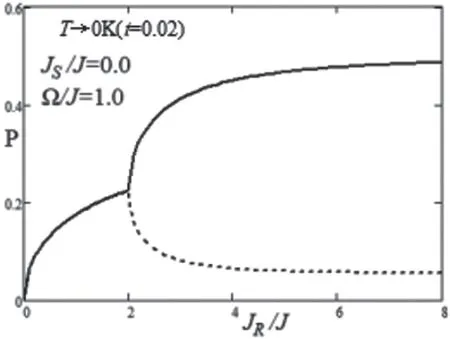
图4 JS/J＜＜1且T→0K时的极化强度P与JR/J的依赖关系图

在图3中，为了和T.Kaneyoshi利用EFT得到的结论进行比较[2]，我们研究了在JR/J=1.0，JS/J=0.0，t=0.02时的极化图P～Ω/J。当初始自旋取向为|0↑↓＞时，用虚曲线MPEL（利用平均场近似的极化强度与横场关系中小的解形成的曲线）描述极化强度与横场的依赖关系，可以发现MPEL的为一“左钩”形形状。MPEL曲线在Ω/J=0.0到0.5区间内单调递增，然后在Ω/J=0.5时达到峰值点 后逐渐单调递减至0，这和T.Kaneyoshi利用EFT获得的曲线趋势大致是一致的。在MPEL曲线的前段为铁电性逐渐增强的过程，在外场Ω/J=0.5时铁电性达到最大，之后铁电性又逐渐变弱，在Ω/J=1.5处转变为顺电相。在此过程经历了两次相变，开始曲线上升的过程为铁电性逐渐增强的过程，可以看成是顺电相转变为铁电相的趋势，MPEL曲线峰值到0的过程可以看成铁电相到顺电相的转变。但是在物理层面，若温度T趋于0K时，且无横场时，铁电体处于基态，各自旋必须完全同向，即Pα=0.5（α=i,a,e），P=0.5，但是此时的P=0.056，自旋取向为|↑↑↓＞，不符合物理规律。

我们通过选取初始自旋取向为|↑↑↑＞，在图3用实线MPEH（利用平均场近似的极化强度与横场关系中大的解形成的曲线）描述极化强度与横场的依赖关系。发现曲线为一阶梯形状，阶梯点恰好为整体曲线又回归了单调递减，此时观察不到重入现象发生。在阶梯点之后，MPEH曲线与MPEL曲线完全重合。也就是说当Ω/J＞0.5时，方程组9仅有唯一解。根据无横场时，零温下极化强度P=0.5，判断可知MPEL曲线才是正解所表示的曲线。

这说明了初始自旋取向选取的不同，利用MFA可能导致在横场Ω/J较小时多解情况的发生，即产生伪解，这意味着我们利用MFA在研究纳米岛相变机制时，一定要符合铁电材料的物理特征，找到符合条件的一组解。

类似地：在Ω/J=1.0，JS/J=0.0时，我们在图4中利用MFA研究了T→0K时的极化强度与层间交换相互作用常数依赖关系P～JR/J，我们和P～Ω/J采用同样的自旋取向|0↑↓＞和|↑↑↑＞，也可以得到两组解，曲线分别记为MPRL（平均场近似下的极化强度随JR/J变化关系值较小的解）和MPRH（平均场近似下的极化强度随JR/J变化关系值较大的解）。我们可以发现MPRL和MPEL形状是完全相同的，MPRH和MPEH形状相同，只是“钩”的方向相反和阶梯方向相反。MPRL和MPRH在JR/J=0.0～2.0范围内完全重合，在JR/J=2.0处分成上下两支曲线，上支MPRH迅速上升，而后趋于平缓至无穷处为一定值P=0.5，下支MPRL以相反的趋势趋于一定值P=0.056处。根据JR/J是增大铁电材料自发强度，然后JR/J趋于无穷大时，极化强度P=0.5，判断得出MPRH才是正解。同时可以得到这样的结论，利用MFA时，在JR/J较大时，可能会产生伪解。

4 结论

本文基于横场Ising模型，在格林函数的框架下，采用通常退耦合近似得到了赝自旋极化强度的x和z分量方程组。发现了在初始自旋取向随机时，相图和极化图可能表现为非常规曲线。这是由于在横场系数较小和层间交换作用常数较大的情形下，方程组存在多解问题。只有在合理的物理角度进行取舍，才能得到能够真正定性描述符合相变机制的解。