基于XFEM的水力压裂裂缝扩展形态研究

熊 佩

(中石化华北油气分公司石油工程技术研究院， 郑州 450006)

裂缝扩展形态是水力压裂理论和现场实施所要考虑的重要因素，对裂缝偏转程度及扩展形态的合理判断是水力压裂成功实施的关键[1-2]。随着计算机仿真技术的发展，数值模拟以其独特的优势成为水力压裂研究的重要手段，而水力压裂数值模拟也从二维模拟发展到了全三维模拟[3]。常用的数值模拟方法有边界元法、非常规裂缝模型模拟法、离散化缝网模型模拟法和扩展有限元模拟法(XFEM)。这些方法各有优缺点，需经过针对性的改进才能更好地模拟真实的页岩储层压裂情况[4]。目前，扩展有限元模拟法多以cohesive单元为基础建立数值模拟简化模型，研究分析不同储层地质参数及天然裂缝发育地层对水力裂缝扩展的影响[5]。

对于水力压裂中孔隙介质的多场流-固耦合问题，可应用ABAQUS软件实现有效建模及求解。在水力裂缝扩展研究方面，目前多采用预设裂缝扩展路径的方式进行模拟分析，其缺点是不能真实地模拟裂缝转向及扩展动态，而扩展有限元法能够很好地弥补这一缺陷[6-7]。经过多年的发展与完善，扩展有限元法仿真技术日渐成熟，可有效地解决水力压裂中的流-固耦合问题[8-9]。

水力压裂裂缝的扩展规律对压裂设计具有重要的参考价值。目前水力压裂裂缝形态扩展研究尚未深入，裂缝扩展形态仍未明晰[10]，因此需要开展基于XFEM的裂缝扩展模拟研究。在本次研究中，将通过XFEM模拟裂缝的扩展形态，分析不同物性参数、施工参数对裂缝形态的影响规律。为了解决水力压裂过程中的裂缝动态扩展问题，应用ABAQUS软件[11]建立水力压裂三维实体模型，基于XFEM法模拟分析射孔方位角、排量、黏度、杨氏模量、泊松比和地应力等多项参数对裂缝扩展形态的影响。

1 水力压裂裂缝扩展数值模型

1.1 预置裂缝模拟射孔

由于射孔尺寸和实际模型尺寸相差较大，因此可通过预置裂缝来模拟射孔。当裂缝插入单元时，单元被分开，同时其内部产生虚拟节点和裂缝尖端。裂缝穿过单元的节点可被赋予额外的自由度，并通过阶跃扩充形函数描述裂缝穿过时形函数的变化。阶跃扩充形函数[4]的表达如式(1)所示：

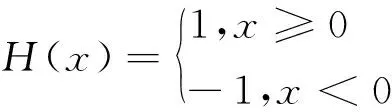
(1)

1.2 基于扩展有限元法XFEM的裂缝扩展模型

对裂缝面和裂缝尖端的描述，是三维裂缝扩展模拟中的一项重要内容。通过2个水平集函数来确定裂缝的位置，水平集函数为符号距离函数[12-13]，如式(2)所示：

φ(x，t)=min‖x-xi‖·

sign[n+·(x-x+)]

(2)

式中：xi——x在裂纹面的正交投影；

n+—— 裂纹面上xi处的外法线投影。

同时，用构造水平集函数的方法来确定裂尖位置。水平集函数可用来描述裂缝尖端的应力奇异问题，如针对水力压裂问题描述不同储层条件和人工控制方法所导致的裂尖应力突变，模拟裂缝在不同应力场条件下的裂尖转向、动态扩展等问题。裂尖水平集函数如式(3)所示：

(3)

式中：r、θ—— 裂尖处的极坐标。

在形函数的基础上形成能够描述裂缝的连续位移场函数(uXFEM)[10]：

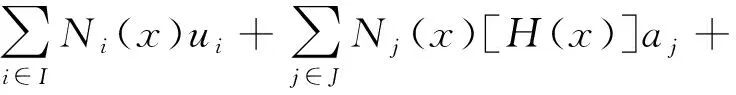
(4)

式中：KL1、KL2—— 1型、2型裂缝尖端的节点集；

F(x) —— 裂尖形函数；

ui—— 标准自由度；

J—— 裂缝穿过单元的节点集；

H(x) —— 阶跃扩展形函数；

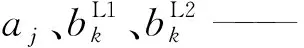
1.3 损伤准则

选择最大主应力准则作为模型裂缝起裂的判定准则，其表达式为：

(5)

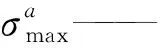
在最大主应力准则的基础上引入能量释放率[14-15]判定裂缝的扩展：

(6)

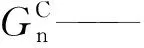
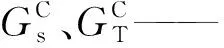
H—— 材料特性常数；

GC—— 复合型裂缝能量释放率，N/mm。

当裂缝尖端的能量释放率大于临界值时，裂缝开始扩展。通过B-K准则与最大主应力准则的联合运用，解决了裂缝起裂和扩展的问题。

1.4 模型参数及边界条件设定

以胜利油田王152区块的岩心数据为基础建立数值模型，相关参数为：岩石弹性模量，10～40 GPa；泊松比，0.22～0.30；水平应力差，2～8 MPa；储层上覆应力，20 MPa；渗透率，25×10-3μm2；滤失系数，58.79 μm/min0.5；压裂液排量，2～14 m3/min；压裂液黏度，20～100 mPa·s；射孔方位角，0～90°；孔隙度，0.25；初始孔隙压力，10 MPa。

根据上述参数建立定压边界模型，通过soil和geostatic模块描述岩石物理力学性质[16]。用裂缝偏转角θ表示裂缝偏转程度。边界条件模型和偏转角如图1所示。

图1 边界条件和裂缝偏转角示意图

2 数值模拟结果分析

数值模拟结果显示，压裂过程中裂缝沿射孔方向起裂，随后发生转向，并沿最大主应力方向扩展[17]。水力裂缝扩展规律如图2所示。

注：E=20 GPa，μ= 0.22，α=60°，v=4 m3/min，Δp=4 MPa。

2.1 射孔方位角对裂缝扩展形态的影响

射孔方位角是射孔与水平最大主应力方向的夹角。模型基础参数设置为：杨氏模量，20 GPa；排量，6 m3/min；黏度，40 mPa·s；泊松比，0.22；水平地应力差，4 MPa，其余与前述参数相同。模拟结果见图3。

注：水平方向为最大主应力方向。

图4所示为射孔方位角与裂缝偏转角关系，从中可看出裂缝有向水平最大主应力方向扩展的趋势。当射孔方位与最大主应力方向一致时，裂缝偏转角为0°；当射孔方位角与最大主应力方向不一致时，裂缝在扩展过程中将发生偏转，且其偏转角与射孔方位角成正相关(近似线性关系)；当射孔方位与水平最大主应力方向垂直时，裂缝偏转程度最大。

图4 射孔方位角与裂缝偏转角的关系

2.2 杨氏模量对裂缝扩展形态的影响

模型主要基础参数为：射孔方位角，60°；排量，6 m3/min；应力差，4 MPa；黏度，40 mPa·s；泊松比，0.22。其余参数与前述参数相同。图5、图6所示为岩石杨氏模量对裂缝偏转角的影响及其关系。

注：水平方向为最大主应力方向。

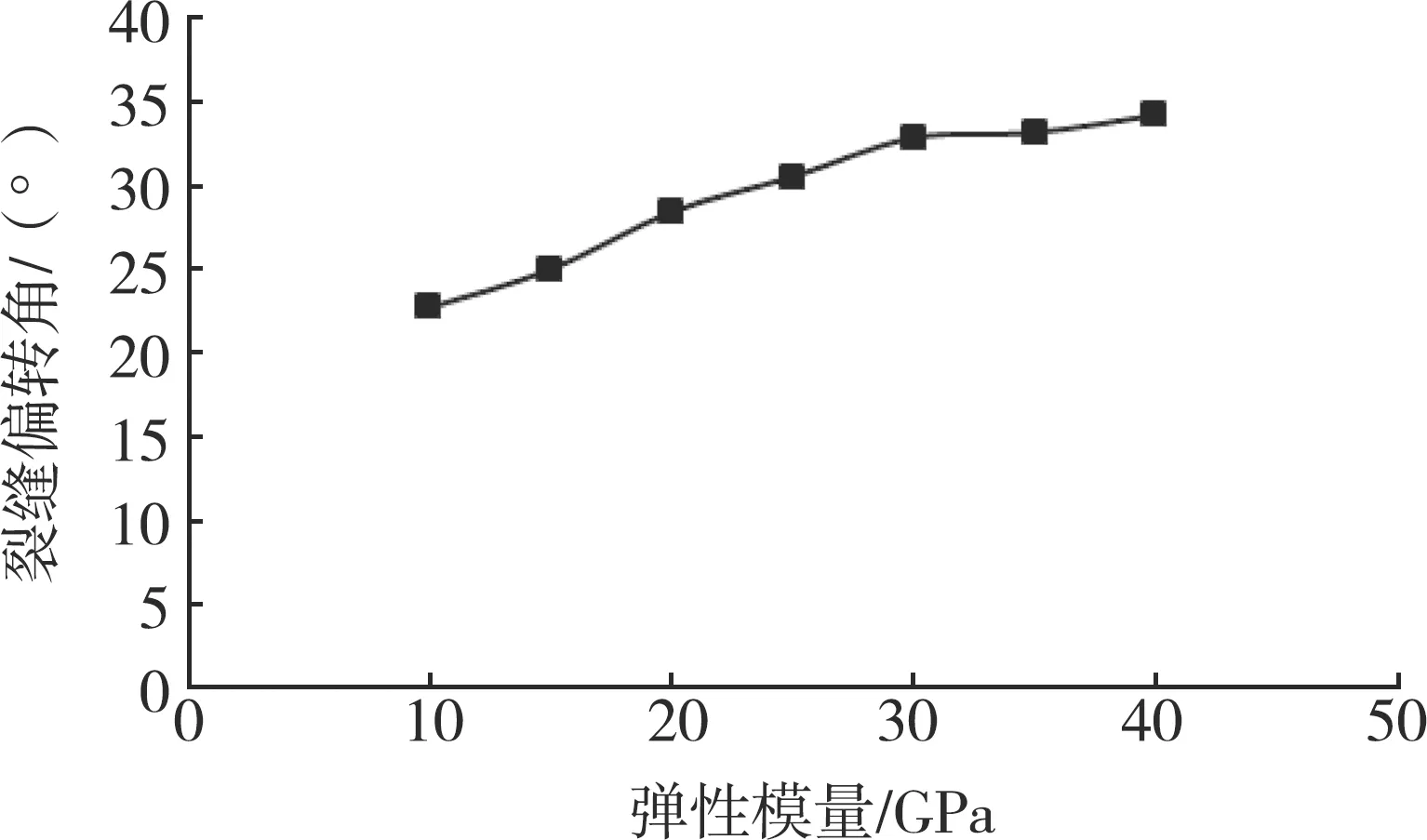
图6 杨氏模量与裂缝偏转角的关系

杨氏模量对对裂缝扩展形态的影响大于对起裂位置的影响。裂缝偏转角与杨氏模量值呈线性正相关，但高杨氏模量条件下，裂缝偏转角的变化幅度较低。

2.3 排量对裂缝扩展形态的影响

模型主要基础参数为：杨氏模量，40 GPa；射孔方位角，60°；水平应力差，4 MPa；黏度，40 mPa·s；泊松比，0.22。其余参数与前述参数相同。图7、图8所示分别为压裂液排量对裂缝转向角、转向位置的影响。图9所示为压裂液排量与裂缝扩展形态的关系。

注：水平方向为最大主应力方向。

图8 压裂液排量对裂缝转向位置的影响

图9 压裂液排量与裂缝扩展形态的关系

数模结果显示，排量对裂缝形态的影响较大，排量越大裂缝偏转半径就越大。在6～14 m3/min排量条件下，裂缝初始偏转距离与排量成线性正相关，同时偏转角与排量成线性负相关。

2.4 水平应力差对裂缝扩展形态的影响

模型主要基础参数为：射孔方位角，60°；排量，6 m3/min；黏度，2 mPa·s；杨氏模量，30 GPa；泊松比，0.22。其余参数与前述参数相同。模拟分析结果如图10、图11所示。

图10 水平两向应力差对裂缝偏转角的影响

图11 水平两向应力差与裂缝偏转角的关系

数模结果显示，裂缝偏转角与水平应力差成线性正相关，旦在高应力差区域裂缝偏转幅度降低。

2.5 压裂液黏度、岩石泊松比对裂缝扩展形态的影响

数模结果显示，裂缝偏转角基本不随泊松比与黏度的改变而改变。模拟结果如图12所示。

图12 岩石泊松比、压裂液黏度对裂缝偏转角的影响

2.6 数据关联分析

对影响裂缝偏转程度的主导因素进行灰色关联分析。根据模拟结果，排除岩石泊松比和压裂液黏度对裂缝偏转角的影响，提取数值模拟中不同的地应力差、杨氏模量、排量和射孔方位角作为自变量，以裂缝偏转角作为因变量，进行统计分析[18]。表2所示为灰色关联分析数据。

表2 灰色关联分析数据(影响因子)

根据计算结果，对影响裂缝形态的因素按其作用从强到弱排序，依次为地应力差、射孔方位角、杨氏模量、排量。

在现场射孔作业中，应保证足够多的射孔数，并使裂缝起裂位于最大主应力方向。在高杨氏模量的地层中，裂缝容易偏转。因此，在压裂设备条件允许的情况下，应提高排量以利于减小裂缝偏转角。

3 结 语

本次研究中，基于ABAQUS有限元软件建立了水力压裂三维实体模型，模拟岩石物性、射孔方位角、地应力、排量等多项参数对水力裂缝扩展形态的影响，应用扩展有限元法对裂缝偏转的主控因素进行灰色关联分析。得到以下认识：

(1) 泊松比黏度对裂缝偏转影响较小。

(2) 杨氏模量、射孔、地应力和排量对裂缝形态有较大影响。

(3) 对裂缝偏转影响最大的因素是地应力，其次为射孔和杨氏模量，排量的影响最弱。

(4) 裂缝偏转程度与地应力、射孔方位角、杨氏模量成正相关，与排量成负相关。在高排量条件下，裂缝偏转程度与排量成线性负相关。