基于回归模型的南海表层漂流浮标轨迹模拟研究

綦梦楠，张娟

（1.国家海洋局南海预报中心，广东广州 510310；2.自然资源部海洋环境探测技术与应用重点实验室，广东广州 510310）

1 引言

利用数模结果和漂移模型开展搜救预测在全球范围内已经得到广泛应用，国外海事发达国家如美国、挪威、加拿大和英国等，已经形成了较为成熟的搜救预测业务化体系[1]。国内，2013年“渤海海上突发事故应急响应辅助决策系统”、“中国近海海上搜救应急辅助决策系统”和2016年“国家海上搜救环境服务保障平台”等搜救保障平台建设完成，为全国各海区的搜救预测提供了保障[2-3]。2019年“基于实测数据的海上搜救优化决策模型研究”项目顺利完成，实现了对海上搜救决策模型的优化提高。此外，国内各海区各类搜救演习和海上搜救综合漂移试验也定期开展，国内搜救预测体系正在发展并逐渐完善。从国内搜救预测系统研究开发和海上搜救试验的区域分布现状来看，各类搜救系统和综合漂移试验以近岸区域研究居多，呈现出“近岸多，远海少”的特点，造成这种现状的原因是多方面的：（1）南海预报中心多年的搜救预测案例结果显示[4]，90%以上的海上事故发生在100 m以浅的近岸海域，不足10%的海上事故发生在100 m以深的海域，近岸海域和远海海域对搜救预测的需求差异明显；（2）远海的观测设备和观测数据稀缺，导致远海区域的漂移预测结果难以验证和提高；（3）远海区域相较近岸区域更难完成仿真人、救生筏和无动力船只的布放、回收和定位。因此，远海区域的搜救预测成为了海上搜救预测的难点。

南海是重要的国际航道，又有丰富的油气资源和渔业资源，南海海域特别是南海深水域搜救预测的准确性，对于海上运输、渔业和海上旅游业等涉海行业的保障意义重大。南海是西北太平洋的半封闭边缘海，地形复杂，岛屿众多，最大深度大于5 000 m，同时，南海又位于季风区，南海表层流动呈现出明显的季节变化。南海海流复杂，其环流的整体结构和变化规律一直是物理海洋学研究中的重要问题之一，南海海流模拟的准确程度直接关系到南海海域搜救预测的准确度。很多学者使用观测数据结合数值模式，对南海的环流结构进行了大量研究，其中，卫星高度计资料和漂流浮标资料具有应用广泛和容易获得的特点，这两种资料被大量地应用到南海表层环流的研究中。方文东等[5]对南海南部的环流及其变化进行了详尽的描述，同时指出未来工作应该将海上现场观测、卫星遥感、数值模拟和理论研究等方法有机结合，深入研究南海的环流结构。Hwang等[6]利用多年的卫星高度计资料计算得到南海环流和涡旋结构的时空变化特征，结合世界海洋环流中心（World Ocean Circulation Experiment，WOCE）的漂流浮标轨迹验证了其结果的可靠性。鲍李峰等[7]利用10 a的卫星高度计资料结合稳态海面地形模型，形成了南海海域合成海面地形的时间序列，计算得到的南海表层地转流场证明了南海表层环流在时间和空间上具有多尺度特征。刘科峰等[8]基于多年卫星高度计资料和漂流浮标资料分析了南海表层流场，描述了南海各季节多年平均的实际流场和地转流场的结构，认为两种流场总体呈现出明显的季节变化特征。Liu等[9]利用漂流浮标资料和基于高分辨率的海洋模式的粒子追踪模型，探究表层黑潮水从北部入侵台湾海峡的可能性，总结了黑潮进入南海的两种不同方式的发生时间。

很多学者的研究表明，海面下10 m平均流场的主要成分是地转流和风海流，表层漂流浮标的速度与地转流和风海流具有较好的相关性[10]。Liu等[11]利用5组基于卫星高度计的流场数据和6组基于海洋环流数值模式的流场数据，使用同一个轨迹预测模型模拟了墨西哥湾18个漂流浮标的轨迹，结果发现无论在深海还是大陆架区域，基于卫星数据的模拟效果优于海洋环流模型数据的预测结果，加入风海流的预测模型比不加风海流的模型效果更好。因此，可以假设使用风海流和地转流可以模拟表层漂流浮标的运动轨迹，并且能够用来校正利用数值模式结果进行漂流浮标轨迹预测的结果。本文尝试建立一个由地转流、风海流和基于区域海洋模式（Regional Ocean Modeling System，ROMS）的表层海流为主要自变量的回归模型，利用拟合的流速模拟浮标轨迹，以期得到更加准确的浮标轨迹预测结果。

2 资料介绍

本文使用的资料主要有表层漂流浮标数据、海表面地转流异常数据、海表面地转流平均场数据、海表面风场数据和ROMS模式表层海流数据。

2.1 表层漂流浮标数据

表层漂流浮标数据来自国家海洋局南海预报中心在南海海域布放的表层漂流浮标，其中4个浮标于2017年12月中旬在南海西南海域布放，另外6个浮标于2019年12月下旬在南海北部海域布放。该浮标为拉格朗日漂流浮标，型号为MLi-S，浮标下挂有1.5 m的漂流幡，漂流幡下挂有配重，浮标外形、尺寸和现场布放过程见图1。在浮标漂移过程中，保证浮标上层弧形保护罩露出水面约2/3，该浮标上层弧形保护罩可以尽可能减小风引起的拖曳应力。浮标通过铱卫星网络通讯，GPS定位，设置的数据接收频率为1 h，每天可以得到24组数据。所有浮标的漂移情况见表1和图2。

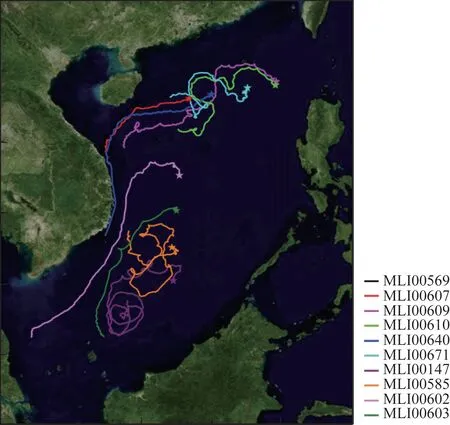
图2 表层漂流浮标轨迹分布图

表1 浮标漂移基本情况

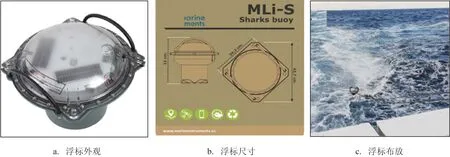
图1 MLi-S型号表层漂流浮标、尺寸和布放

2.2 海表面地转流异常数据和海表面地转流平均场数据

地转流资料是法国国家空间研究中心卫星海洋学存档数据中心（Archiving Validation and Interpolation of Satellite Oceanographic data，AVISO）提供的利用TOPEX/POSEIDON和ERS-1/2等多颗高度计卫星数据融合得到的Ssalto/Duacs海表高度异常和地转流（异常）数据。使用的数据时间范围从2017年12月—2018年2月和2019年12月—2020年2月，共6 M，时间分辨率为1 d，空间分辨率为1/4°。AVISO根据1993—2012年的海表面高度数据得到该段时间的平均海表面高度，进而计算得到海表面地转流平均场数据，其空间分辨率为1/4°。

2.3 海表面风场数据

海面风采用国家海洋局南海预报中心业务化气象预报系统的风场预测结果。系统采用WRF（Weather Research and Forecasting）模式，预报区域分为两重嵌套。大区域范围93.99°～156.00°E，4.77°S～45.35°N，麦卡托投影上的水平格点为201×181，空间分辨率30 km。小区域范围97.94°～129.62°E，0.52°～28.63°N，麦卡托投影上的水平格点为381×369，空间分辨率8.4 km。垂直坐标分为不等距27层，顶层取50 hPa，模型结果的时间分辨率为1 h。该业务化预报模型已使用多年，从模型10 m风结果与南海8个浮标站点的观测数据对比来看，24 h预报的风速平均误差在1.8 m/s左右，风向平均误差为20°左右，能够较好地模拟南海海域的风速和风向。

2.4 ROMS模式表层海流数据

表层海流数据来自国家海洋局南海预报中心业务化海流预报系统的海流预测结果，其模拟区域为99.08°～144.94°E，4.42°S～28.26°N，水平格点为985×793，采用变网格结构，在南海海域的水平空间分辨率为1/30°，垂向分层为35层。模式地形数据采用ETOPO1全球海洋地形数据，模型最小水深为10 m，最大水深为6 000 m，模型上边界强迫采用2.3节南海预报中心业务化海表面风场数据，温盐开边界数据采用全球简单海洋资料同化分析系统（Simple Ocean Data Assimilation，SODA）的再分析资料，模型结果的时间分辨率为1 h。该海流模型为国家海洋环境预报中心构建的全球-大洋-近海3级嵌套的全球业务化海洋学预报系统体系中的中国近海海洋环流数值预报子系统中的一部分[12]，对于南海区域的温度、盐度和流速模拟具有较好的准确性。

3 浮标特征分析

2019年12月底布放的表层漂流浮标主要分布在南海北部海域，其中MLI00569、MLI00607和MLI00640号浮标的轨迹主要沿南海北部往西北部的陆坡运动，运动轨迹较为平直，运动方向变化平缓；MLI00609、MLI00610和MLI00671号浮标则在南海东北部的涡旋区域运动，在涡旋显著的海域其运动轨迹受局地的涡旋控制而呈现出近似半封闭的圆。

2017年12月中旬布放的表层漂流浮标主要分布在南海西南部，其中MLI00602和MLI00603号浮标在南海西南海域靠近大陆架的区域运动，其轨迹总体较为平直，运动方向变化也较为平缓；MLI00147和MLI00585号浮标的运动轨迹则分布在南海西南部涡旋控制区域，其轨迹较为复杂，浮标的轨迹呈现出封闭或者半封闭的圆。

4 回归模型和检验标准

4.1 建立回归模型

通常情况下，海面下10 m内的平均流场主要受风海流和地转流的影响，表层漂流浮标的漂移速度与风海流和地转流具有一定的相关性。为体现回归模型中各个自变量的作用，建立了3个回归模型。模型1使用地转流和风海流作为自变量，利用回归模型探究它们与浮标漂移速度的关系，检验风海流叠加地转流后的拟合流场是否能够较好地模拟浮标轨迹。模型2使用ROMS模型结果作为自变量，利用该模型研究数值模式对浮标漂移轨迹模拟的准确性。模型3将风海流、地转流和ROMS模型结果都当作自变量，使用风海流和地转流订正ROMS海流模型的结果，检验在数值模拟结果的基础上加入风海流和地转流后能否对数值模型结果有所提升。3个回归模型如下所示：

（1）基于风海流和地转流建立回归模型（M_EG）

式中，（u10、v10）为海表面10 m风速；（ug_ave、vg_ave）为海表面地转流平均流流速；（ug_ano、vg_ano）为海表面地转流（异常）流速。

（2）基于ROMS模型结果建立回归模型（M_R）

式中，（uroms、vroms）为ROMS模型表层海流流速。

（3）基于风海流、地转流和ROMS模型结果建立回归模型（M_EGR）

M_EGR模型中所有自变量均与M_EG和M_R模型中意义相同，a0～a5和b0～b5在不同的回归模型中数值不同。

在回归分析中，所有数据的时间间隔为1 h。海表面10 m风速和ROMS模型表层海流流速的时间分辨率与浮标漂移轨迹数据相同，均为1 h，风速数据和流速数据采用双线性插值将网格数据插值到浮标所在位置；海表面地转流平均流流速和海表面地转流（异常）流速的时间分辨率为1 d，时间上采用线性插值，空间上采用双线性插值，将地转流数据插值到浮标所在的位置。以上模型变量中速度的单位为m/s。

4.2 浮标轨迹模拟

利用4.1节中回归模型统计得到相关回归系数后，代入相对应的式（1）、（2）、（3）中，得到模拟流速，以M_EGR模型为例：

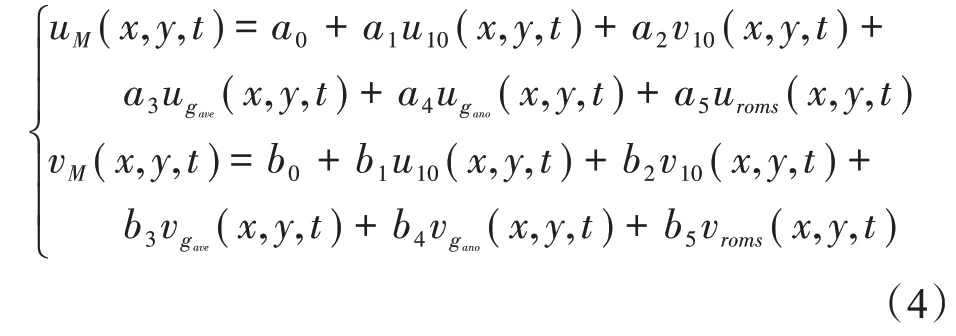
时间积分采用四阶精度的经典龙格-库塔方法求解[13-14]，即可得到模拟浮标轨迹，积分时间步长Δt为10 min。

4.3 模型检验标准

对于所有漂移轨迹，每隔24 h做一次72 h的浮标漂移轨迹模拟，然后利用模拟结果与浮标漂移轨迹进行距离误差、角度误差和综合技术得分的统计对比。

距离误差（L）：漂移轨迹的距离误差为某时段内模拟轨迹的终点与漂移轨迹终点的距离。

角度误差（D）：漂移轨迹的角度误差为某时段内模拟轨迹终点跟起始位置连线与漂移轨迹终点跟起始位置连线的夹角。

综合技术得分（s）：利用标准化累积间隔距离（c）和公差阈值（n）计算得到，能够反映模型的模拟效果。s值越大，模拟效果越好，s值越小，模拟效果越差，s取值范围为0～1[15-17]。

式中，n为公差阈值，是一个无量纲的正数，其定义了模拟轨迹s=0时c的值。n取值越大，对模型的要求越低，n值越小，则表示对模型的要求越严格。本文借鉴Liu等[11]在对墨西哥湾的漂流浮标的轨迹模拟分析中根据约27%的浮标位置的模拟轨迹的s=来确定n的取值。通过分析M_EGR模型的c的分布规律，我们得到约30%浮标点s=0时的n的取值为1.5，即当模拟轨迹与浮标轨迹之间的累积间隔距离超过1.5倍的浮标轨迹的累积长度时，其s=0。c即为累积间隔距离（d）与浮标轨迹的累积长度（l）的比值。

式中，i的取值范围为i=1,2,…,N，N为总天数。图3为模拟轨迹与漂移轨迹点之间d和l的图解说明。图中A—B段为模拟结果，记作lm；A—C段为实测结果，记作lo；l1、l2和l3分别表示从模拟起始时刻起第1 d、2 d和3 d的实际漂移距离，d1、d2和d3分别表示从模拟起始时刻起第1 d、2 d和3 d模拟轨迹与漂移轨迹点的间隔距离。在一段模拟时间内，模拟结果与实测结果位置越接近，d值和c值越小，s越高，模拟效果越好。当模拟轨迹与浮标轨迹完全重合时，s值为1。

图3 模拟轨迹（A—B段）与浮标轨迹（A—C段）之间d和l图解

5 模拟效果比较

ROMS海流模式结果中包含风海流和地转流的成分，可看作地转流、风海流和其他因素共同作用下的流动三者合成的海流，然而各成分在整体流速中所占比例无法计算，只能作为一个整体考虑。M_EG模型自变量选取了风海流和地转流来拟合漂流浮标轨迹，风海流和地转流中各项的系数可以不同；M_R模型的自变量选择了ROMS模式的结果，M_R模型中风海流、地转流和其他因素引起的流动只能作为一个整体使用同一个系数；M_EGR模型可以认为是使用M_EG模型中系数可以自由调整的风海流和地转流来订正不能自由调整系数的M_R模型中风海流、地转流和其他因素引起的流动。将10个浮标所有轨迹的数据经过处理后，利用M_EG、M_R和M_EGR 3个回归模型分别计算各个模型u和v方向各个自变量的系数（见表2和表3），将各个系数代入到回归模型中计算得到拟合的流速值，进而得到模拟的浮标轨迹。

表2 3个回归模型中u方向各个自变量的系数

表3 3个回归模型中v方向各个自变量的系数

利用M_EG、M_R和M_EGR模型分别模拟表层漂流浮标轨迹，3个模型24 h、48 h和72 h的平均距离误差和平均角度误差见表4。表中可以看出随着预报时间的增长，3个模型的平均距离误差均增大，平均角度误差变化不大。为方便描述，本节主要对72 h的模拟结果进行解释分析。图4—6分别为3个模型72 h平均距离误差、平均角度误差和标准化累积间隔距离的频率分布图。各模型72 h平均距离误差分别为42 km、48 km和38 km，距离误差的标准差分别为25 km、29 km和23 km，最小距离都为1 km，最大距离分别为182 km、156 km和143 km；各模型72 h平均角度误差分别为36°、40°和35°，角度误差的标准差均为39°；标准化累积间隔距离分别为1.42、1.47和1.26。可以看出，M_R模型的平均距离误差和平均角度误差在3个模型中最大，其对应的标准化累积间隔距离也最大；M_EGR模型的平均距离误差和平均角度误差最小，其对应的标准化累积间隔距离也最小，标准化累积间隔距离与平均距离误差和平均角度误差具有很好的一致性。以MLI00603号浮标为例（见图7），浮标漂移时间是从2017年12月9日—2018年1月8日，s较低（s<0.1）的位置主要在浮标开始运动的前6 d，其原因主要是该区域流速较弱，风力也不强，浮标未受到较为持续稳定的作用力，导致浮标轨迹较为发散，s较低；从2017年12月15日开始，浮标轨迹的s主要在0.4～0.7之间，部分时段能够超过0.7，是因为该区域具有较为持续稳定的偏南向流动[8]（见图8），这一结论从地转流和ROMS模式中均可以看出。

图4 模拟轨迹与漂移轨迹72 h距离误差频率分布图（mean：平均值，std：标准差，min：最小值，max：最大值）

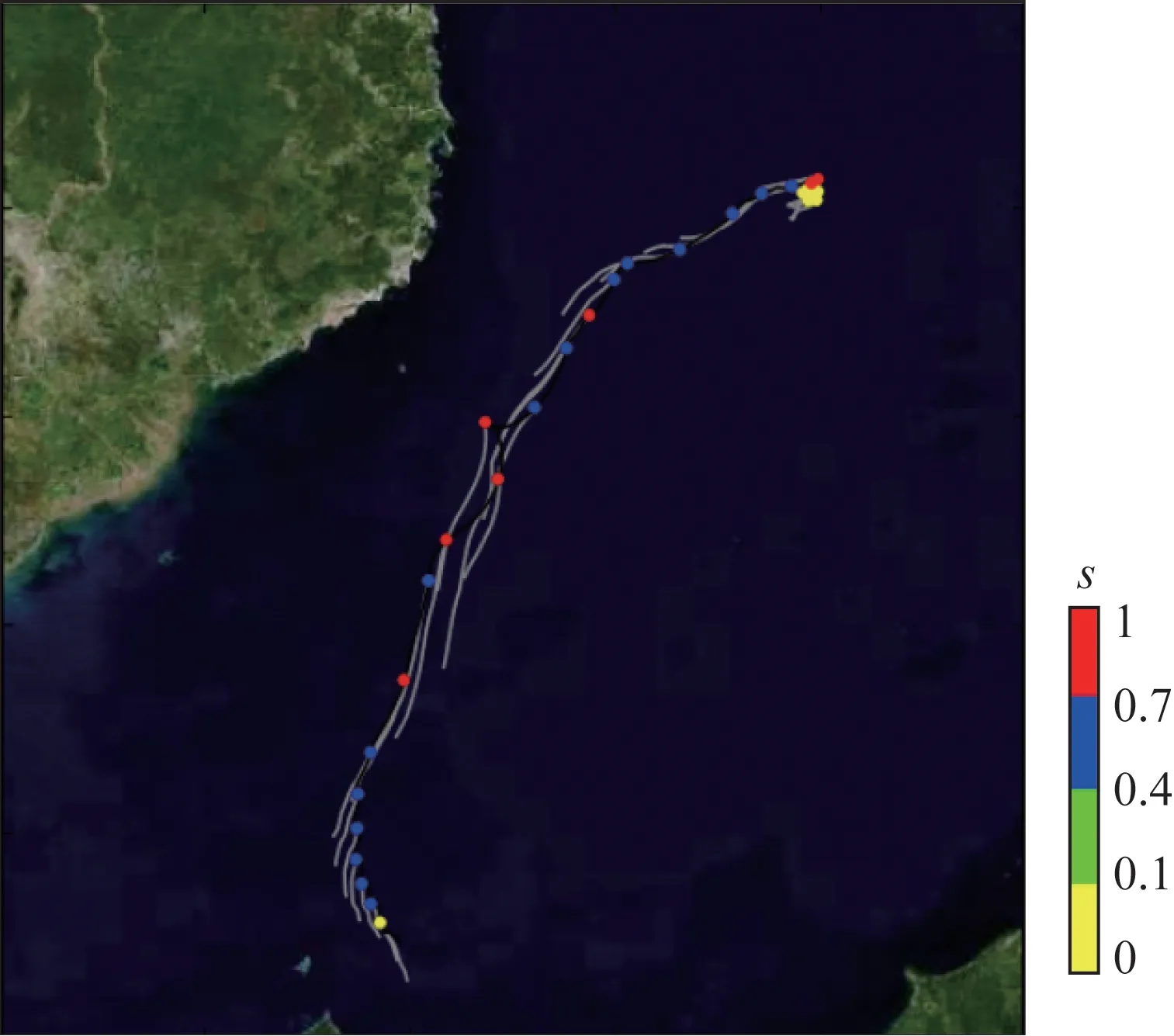
图7 MLI00603号浮标模拟轨迹（灰色）与漂移轨迹（黑色）分布（漂移轨迹中闭合圆圈颜色代表该点的s）

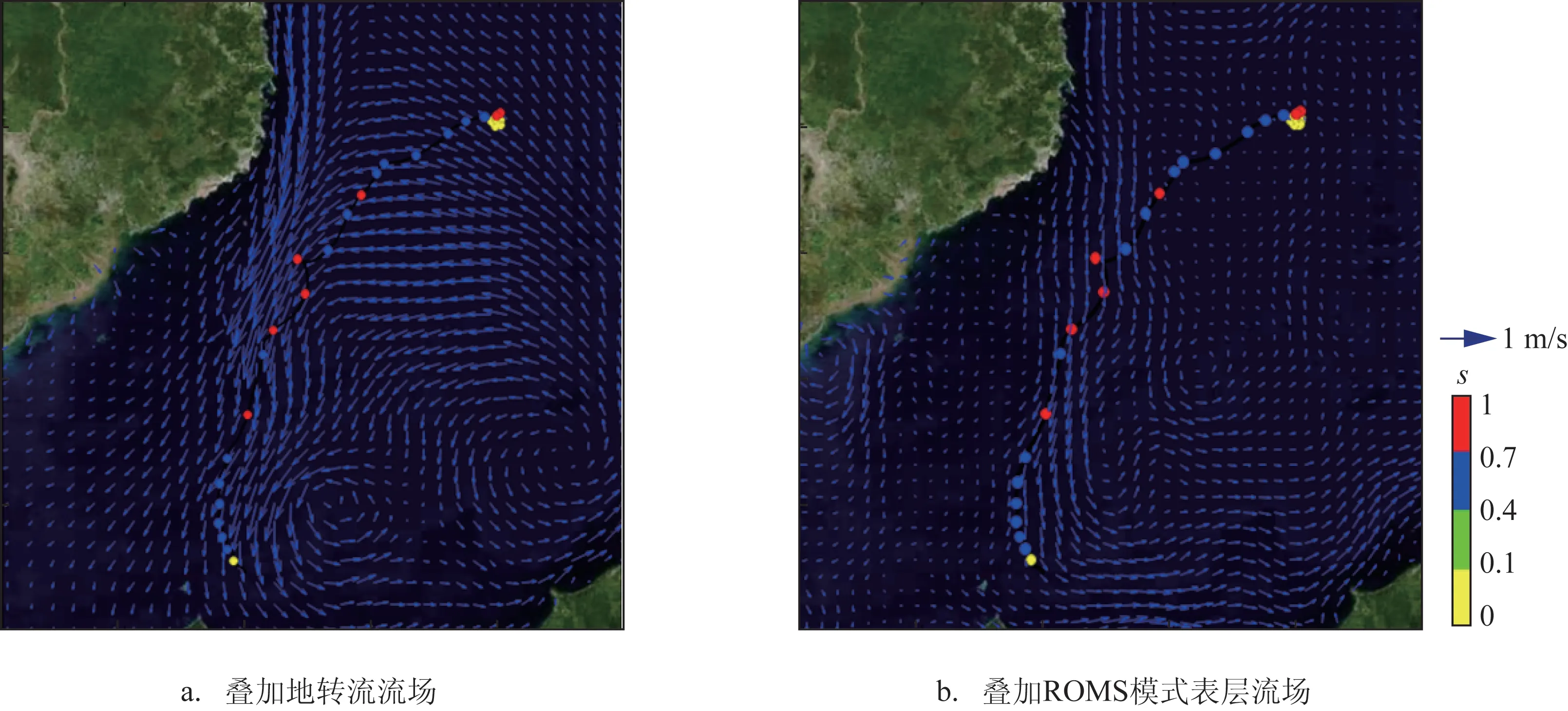
图8 MLI00603号浮标漂移轨迹（黑色）分别叠加地转流流场和表层流场结果

表4 3个模型24 h、48 h和72 h平均距离误差和平均角度误差统计表

根据3种模型模拟浮标轨迹与漂移轨迹的距离误差空间分布可以看出（见图9），3个模型72 h模拟结果中30%～50%的点的距离误差小于30 km。M_EG模型中距离误差小于30 km的区域主要分布在南海北部、中部偏西海域和西南区域，M_R模型中距离误差小于30 km的区域主要分布在南海西北部海域、南海中部海域和南海西南部大陆架附近海域；M_EG模型在南海北部和西南部涡旋较为显著区域的距离误差比M_R模型小，M_R模型在南海海盆边缘和大陆架区域的距离误差比M_EG模型小，M_EGR模型能够综合前两个模型的优点，对很多区域的距离误差有所降低。由3种模型模拟浮标轨迹与漂移轨迹的角度误差空间分布来看（见图10），3个模型中60%～70%的点的角度误差小于30°，其分布区域遍布南海北部海域、中部偏西海域和南海西南海域，角度误差偏大的区域主要在流速较小的海域。此外，由于文中使用的高频浮标轨迹（1 h）可能包含有潮流信号，在进行回归分析时未包含潮流分量，这也可能是导致3个模型产生误差的因素之一。

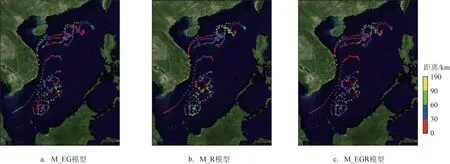
图9 3种模型模拟轨迹与漂移轨迹72 h距离误差空间分布

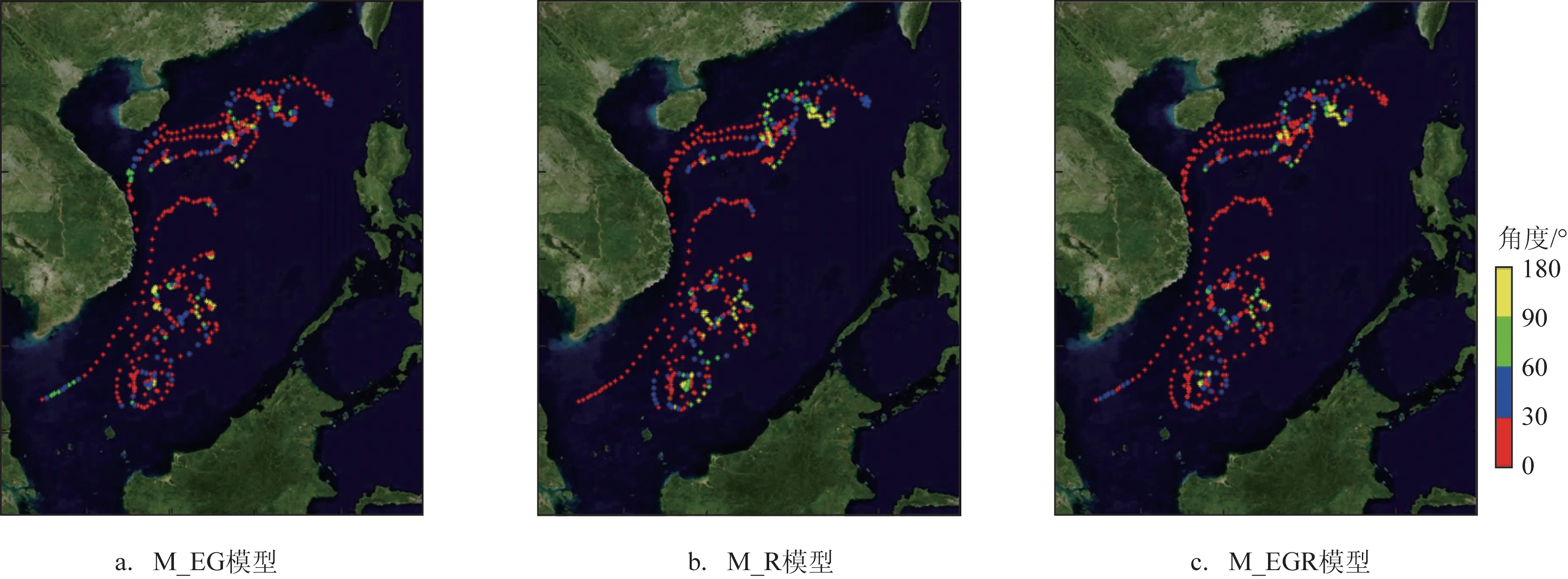
图10 3种模型模拟轨迹与漂移轨迹72 h角度误差空间分布

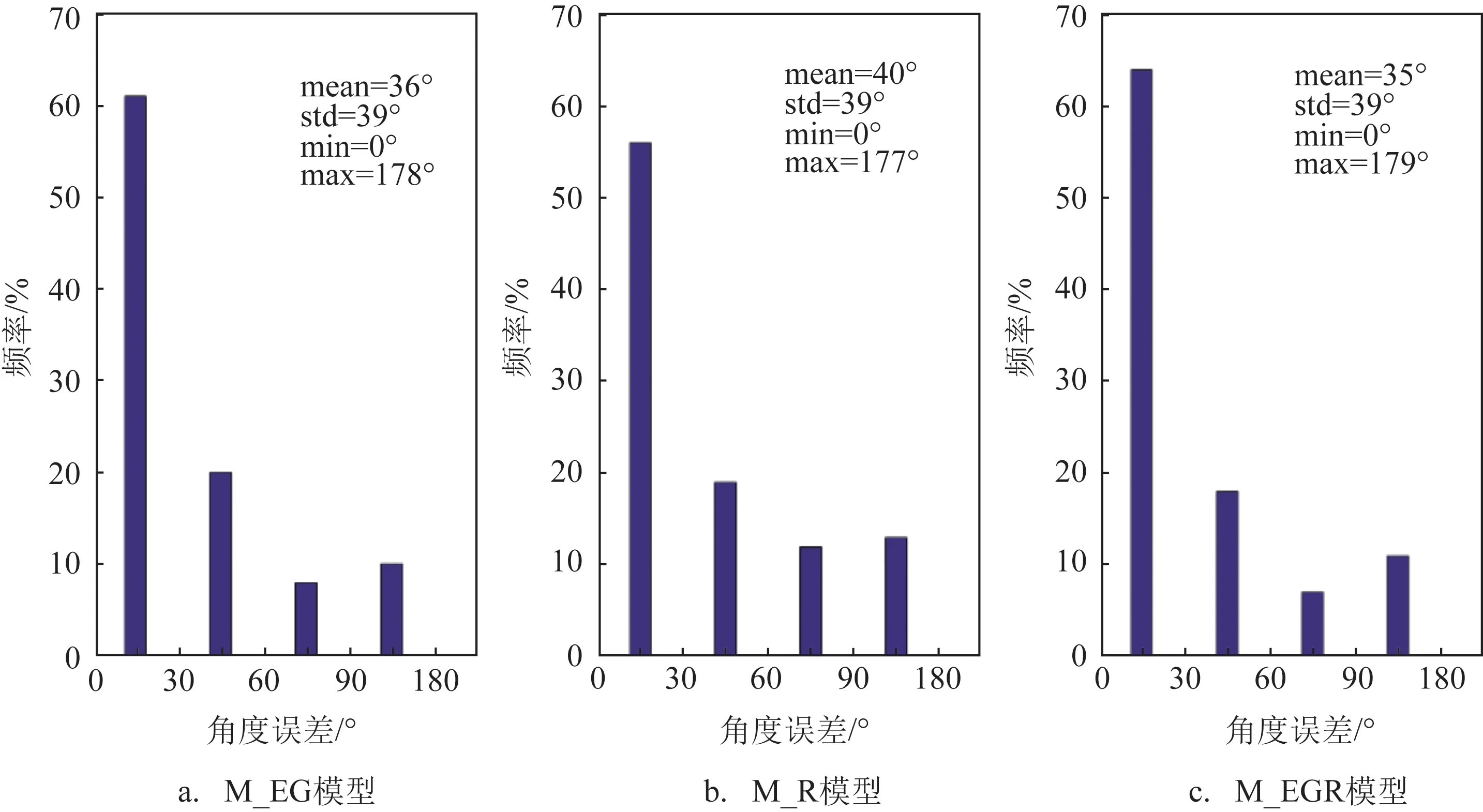
图5 模拟轨迹与漂移轨迹72 h角度误差频率分布图（mean：平均值，std：标准差，min：最小值，max：最大值）

图6 模拟轨迹与漂移轨迹72 h标准化累积间隔距离频率分布图（mean：平均值，std：标准差，min：最小值，max：最大值）

图11 为3种模型模拟轨迹72 h模拟结果s的空间分布。在M_EG模型中，s高于0.4的区域主要在南海北部部分海域和南海西南部冬季强流区以西海域，s平均为0.30，由于地转流数据在近岸区域和浅水区误差较大，海南南部、越南东部和泰国湾以东附近区域的模拟效果较差，s低于0.4；M_R模型中，s高于0.4的区域主要在南海西南部靠近海盆边缘的大陆架附近和南海西南部冬季强流区以西海域，s平均为0.25，ROMS模式在开阔海域对于中尺度涡位置和范围的模拟难度较大，导致模型在南海西南部和北部开阔海域模拟效果不理想；在M_EGR模型中，南海北部海盆边缘和大陆架区域、南海西南部和中部流速较为稳定海域的s大于0.4，在南海北部东沙群岛以南海域和南海西南海域的多涡旋区域的s小于0.4，与该区域涡旋多、位置变化较大有一定的关系，M_EGR模型的平均s为0.34，较M_EG模型提高了0.04，比M_R模型提高了0.09。

图11 3种模型模拟轨迹72 h综合技术得分空间分布

6 预报可行性分析

综合上面讨论的3个回归模型，M_EGR回归模型对浮标轨迹的拟合效果最好，因此在本节中使用M_EGR模型对浮标轨迹预报进行可行性分析实验。实验方法如下：将10个浮标轨迹中的任意9个浮标的漂移速度数据进行回归分析，得到各个变量的系数后计算拟合的速度，然后预报余下的一个浮标的轨迹，统计其24 h、48 h和72 h距离和角度的平均误差，总共进行10个浮标的轨迹的误差统计。利用该方法得到的误差统计结果作为实验组结果，上一节中利用所有浮标轨迹进行回归分析得到的轨迹模拟作为对照组，实验组和对照组误差统计结果见表5。

通过表5可以看出，实验组平均距离误差比对照组偏大，24 h、48 h和72 h的误差分别偏大2 km、4 km和6 km；实验组平均角度误差略大于对照组。这是因为对照组将预报检验的浮标轨迹得到的速度也进行了回归分析，得到的各变量的系数比实验组更接近预报检验的浮标的系数，因此平均距离误差和角度误差要优于实验组。实验组和对照组72 h的平均距离误差分别为44 km和38 km，与Liu等[11]利用11组数据在墨西哥湾水深区域中模拟18条漂流浮标轨迹后计算得到的72 h平均距离误差83 km相比，模拟效果相对更好。

结合图2和表5可以发现，10个浮标中漂移轨迹较为平直的MLI00569、MLI00607、MLI00640、MLI00602和MLI00603浮标的拟合效果明显好于漂移轨迹复杂多变的MLI00609、MLI00610、MLI00671、MLI00147和MLI00585，各浮标的平均角度误差体现得特别明显。崔凤娟等[18]利用Okubo-Weiss函数方法对20 a的高度计资料进行了涡旋识别分析，结合前人的研究基础[19-20]，认为涡旋个数没有明显的季节性，但在夏季容易产生反气旋涡，冬季容易产生气旋涡，冬季的气旋涡主要分布在吕宋岛西北和越南外海。这些特征从浮标轨迹、地转流场和数值模型流场结果中能体现。然而赵新华等[21]在使用1993—2015年高度计涡旋数据集的欧拉涡旋匹配相同时段内浮标漂流轨迹提取的拉格朗日涡旋[22]时发现，20°S～20°N区域内匹配成功率不足10%，卫星高度计无法观测到欧拉涡旋区域存在大量拉格朗日涡旋，在南海区域涡旋匹配成功率为17.4%。这从另一个方面说明使用欧拉流速拟合拉格朗日流速具有很大的挑战性。

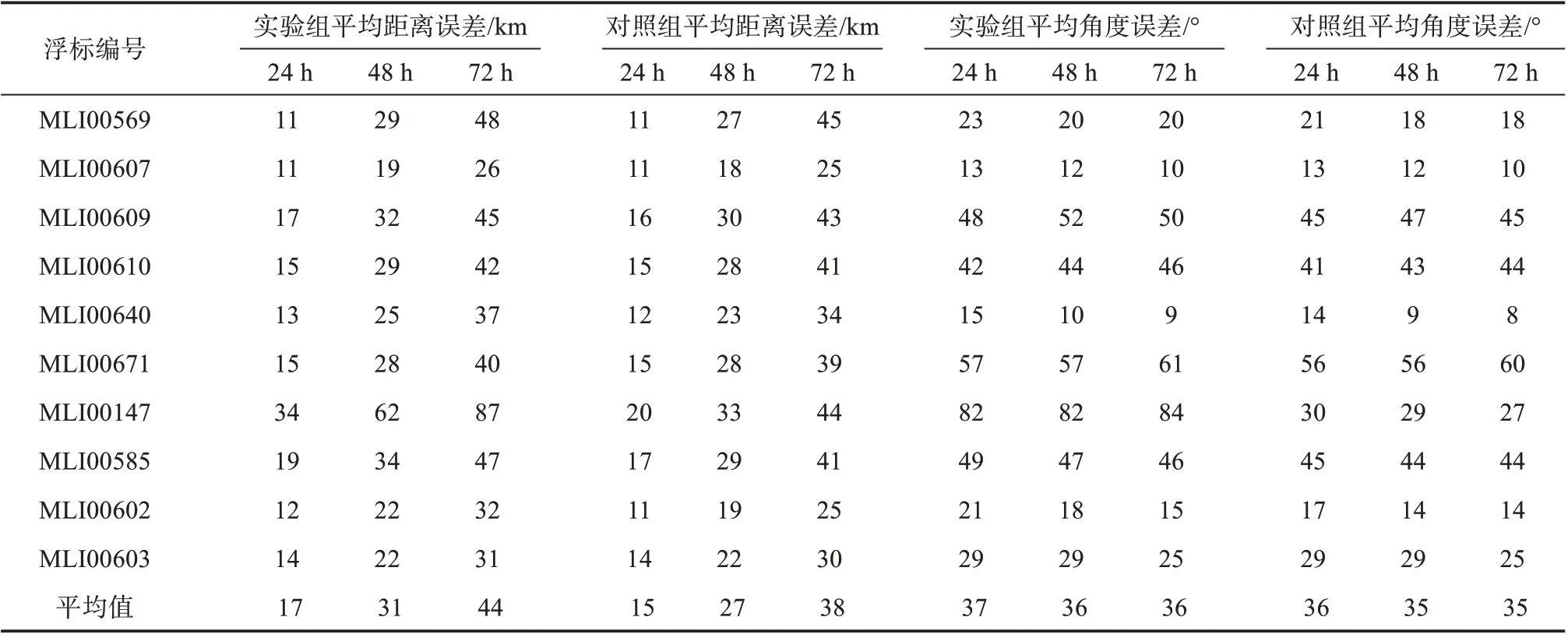
表5 实验组与对照组平均距离误差和平均角度误差统计

冬季，南海受东北季风的影响显著，其环流呈现出复杂多变的特性，受多种因素的影响，很多涡旋的形状、强度和移动变化较快；此外浮标运动对浮标的初始状态和外力非常敏感，实验显示投放点相邻的几个浮标会呈现出截然不同的运动轨迹。因此在涡旋较为活跃和季风较强的区域和时段内，容易出现浮标运动轨迹复杂和模拟效果较差的问题。

综合来看，对于南海流速较为稳定的区域，使用M_EGR回归模型拟合的流速与浮标的漂移速度符合较好，可以较为准确地模拟浮标的漂移轨迹；在南海涡旋较多的区域，模型模拟效果有待提高，可以通过增加该区域内浮标轨迹的数量提高回归模型的准确性，使回归模型中各自变量的系数对涡旋的特点体现更准确，从而更好地模拟浮标轨迹。

7 结论与讨论

本文利用海表面地转流异常数据、海表面地转流平均场数据、海表面风场数据和ROMS模式表层海流数据中的一项或者多项作为回归自变量，建立了M_EG、M_R和M_EGR 3个表层浮标漂移速度回归模型，模拟了2017年12月—2018年2月和2019年12月—2020年2月的南海海域表层漂流浮标轨迹，通过模型结果与浮标轨迹进行对比分析，得到以下结论：

（1）利用M_EG、M_R和M_EGR模型分别模拟表层漂流浮标轨迹，各模型72 h平均距离误差分别为42 km、48 km和38 km，距离误差的标准差分别为25 km、29 km和23 km，平均角度误差分别为36°、40°和35°，角度误差的标准差都为39°；标准化累积间隔距离分别为1.42、1.47和1.26；s平均分别为0.30、0.25和0.34。3种模型中，基于地转流、风海流和ROMS模式表层海流3项作为自变量的M_EGR回归模型效果最好。

（2）M_EG、M_R和M_EGR模型中30%～50%的点的距离误差控制在30 km以内，60%～70%的点的角度误差小于30°。在M_EG回归模型中加入ROMS模式表层海流结果后，72 h平均距离误差减少4 km，平均角度误差减少1°，s平均提高0.04，模拟结果提高的区域主要在南海海盆边缘和大陆架附近海域；在M_R回归模型中加入地转流和风海流后，72 h平均距离误差减少10 km，平均角度误差减少5°，s平均提高0.09，模拟结果提高的区域主要在南海北部和西南部涡旋较为显著区域。风海流叠加地转流数据与ROMS模式资料在南海表层浮标轨迹的预测方面具有较好的互补性，该方法对利用数值模式结果进行漂移浮标轨迹预测具有较好的订正效果。

（3）在南海流速较为稳定的的区域，采用M_EGR回归模型可以较好地拟合浮标的漂移速度，对浮标漂移轨迹的拟合情况较好；在南海涡旋较多的区域，受涡旋形状、强度和移动变化较快等因素的影响，漂流浮标轨迹模拟效果不如非涡旋区，可以通过增加该区域内浮标轨迹的模拟数量提高回归模型的准确性，从而更好地模拟浮标轨迹。

本文使用时间间隔为1 h的高频浮标轨迹数据可能包含有潮流的信号，在进行回归分析的流场中未包含潮流分量，这也可能是导致3个模型产生误差的因素之一，之后可以尝试对浮标速度进行适当的滑动平均进行分析，再利用回归模型对表层漂流浮标轨迹进行模拟分析。此外，不同区域的涡旋特点不同，可以通过搜集更多的漂移浮标资料进行分析和模拟，以增加回归模型对涡旋区域浮标轨迹模拟的准确性。