基于线性误差断言的推理方法
武 鹏,吴尽昭,2,3,4*
(1.北京交通大学计算机与信息技术学院,北京 100044;2.中国科学院成都计算机应用研究所,成都 610041;3.广西大学计算机与电子信息学院,南宁 530004;4.广西民族大学人工智能学院,南宁 530006)
0 引言
形式化验证属于形式化方法的范畴,形式化验证主要包含两种方法,模型检验和定理证明。模型检测是由Clarke和Emerson提出的,主要通过搜索系统状态空间来验证系统的正确性的一种方法[1]。而定理证明主要解决如何利用逻辑和数学推理证明的手段验证软件的关键性质。这两种方法优势互补,在学术界[2-3]、工业界[4]得到了广泛应用。定理证明中的推理方法是演绎推理范畴,其中语法、语义、推理规则涉及其中,许多学者在这一领域有广泛的深入研究[5-6]。标签变迁系统或其相似结构广泛应用在模型检验和定理证明相关的验证领域,它是刻画系统的变迁行为的常用技术手段[7]。其中,系统各个状态及变迁条件通过相应逻辑赋值及其满足的条件来刻画。然而,二值或多值逻辑在描述复杂系统的状态并不完全有效[8]。实多项式代数变迁系统将二值逻辑和多值逻辑的状态空间扩展到Rn域,这在描述复杂系统行为和验证复杂系统安全性质上更有效[9]。近年来,在混成系统的验证领域,微分多项式代数和不变量理论[10-11]相继被提出,这进一步地拓宽了基于定理证明的推理方法的应用领域。
另一方面,在复杂系统中,系统参数有时并不是精确确定的,大多数情况下只知道这些参数的取值范围,这增加了这些系统的推理验证工作的难度。例如,许多基于多项式的定理证明系统中广泛运用了Grobner基方法,然而多项式方程组的Grobner基对系数是不连续的[12],这大大增加了推理验证方法处理误差参数多项式系统的难度。而系统的误差又是普遍存在的。工程上,在验证系统某些性质的过程中,对变迁条件的刻画是确定的数值,而这恰恰是工程上无法做到的。例如,当系统温度等于90°时,停止供热。但实际中,无法精确测量温度刚好到达90°,测量的过程都伴随着一定的误差。在系统变迁的过程中,往往有若干个阈值条件来触发系统的变迁,这就需要对这若干个系统参数精确测量。而事实上,这是不可能做到的,测量的过程总是伴随着一定的误差。多个误差变量的累计和传递过程中,系统可能出现错误的变迁行为。是否能定量地将误差参数结合到推理方法中,并应用于含误差参数系统的推理验证工作中?笔者在文献[13]中给出了线性误差断言零点集的凸集性的证明,但未给出求线性误差断言所有顶点的方法和相关证明;而求取这些顶点是文本方法步骤的必不可少的环节,也是实现本文方法的难点。本文给出了求线性误差断言顶点的具体方法并证明了该方法的正确性,之后给出文本方法在验证火车加速状态的应用,求取了火车加速状态的参数化顶点,将看似非线性问题处理为线性问题,进一步扩大了本文方法的应用范围。这在以往的文献中是鲜有报道的。本文给出的推理方法可用于线性误差系统的推理验证工作中。
1 误差的区间数刻画
误差是普遍存在的,有时也是必不可免的。在推理方法中引入误差,就需要对误差做定量刻画。误差常常是限定的一个区域,而区间数是数的推广,区间数在许多方面已经成功应用[14-16],下面介绍区间数的运算规则。

区间数是实数的推广,当a-=a+时,-a为实数。然而上述定义的区间数的四则运算是不可逆的,下面给出例子。
若a为实数,则式(1)则一定成立。然而若a,b为区间数,式(1)不一定成立。


但这并不意味着包含上述四则运算的推理过程是错误的,只是推理过程不可逆,即推理的结论是前提的一个必要条件,而非充分必要条件。在包含误差的推理的过程中,运算次数的增多,可能会导致结果没有实际意义,所以在推理过程中,要尝试其他方法。本文的方法提供了一种思路。
2 线性误差断言及蕴含关系
2.1 线性误差断言

2.2 蕴含关系
蕴含关系是基于定理证明的形式化验证领域重要环节,也是推理规则的基础问题。φ1蕴含φ2表示:如果φ1为真,则φ2一定为真。记作φ1|=φ2。例如:φ1:x-1=0,φ2:x2-1=0,显然有:φ1|=φ2。基于多项式断言的蕴含关系[17]中有这样一个充要条件:φ1|=φ2的充分必要条件为Zero(φ1)⊆Zero(φ2)。这同样适用于线性误差断言。下面给出线性误差断言的蕴含关系的充分必要条件。

3 推理方法



4 实例分析
4.1 火车加速状态分析
下面以火车加速运动为例分析。为了便于分析,假设火车有2个车厢(8车厢和16车厢问题可由两车厢问题递归得到),两车厢各有动力输出。火车在加速过程中,当————guard为v=80 m s=288km h满足时,火车由加速状态转变为匀速状态(由图1所示),-φ、-ϕ为加速状态和匀速状态各自正常工作满足的条件。在火车的加速状态中,如果-φ不满足,则火车加速状态异常,需立即检测异常。
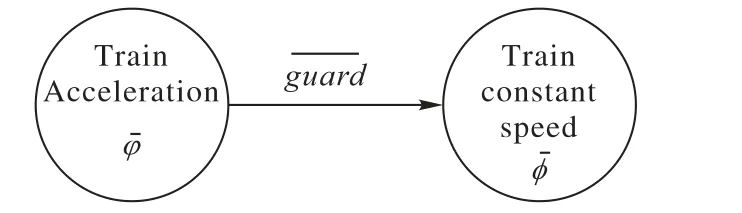
图1 火车状态变迁Fig.1 Train state transition
f1、f2分别表示车厢1与车厢2各自提供的牵引力。f12为车厢1对车厢2的作用力,为一区间数。m1、m2代表每个车厢的初始质量。Δm1、Δm2代表车厢的质量变化(由于乘客和行李的变化),为区间数。ζ是一个关联空气密度压强的系数,由于风、海拔等因素的变化,ζ为区间数。a表示加速度。g为重力加速度。
下面给出上述变量值,m1=50 000 kg,Δm1=[0,0.2m1],m2=50 000 kg, Δm2=[0,0.2m2],ζ=[1.5,1.6]kg m,μ=0.01,a=0.4 m s2,f12=[0,2 000]N,g=10 m s2。
由力学知识,可有式(20):
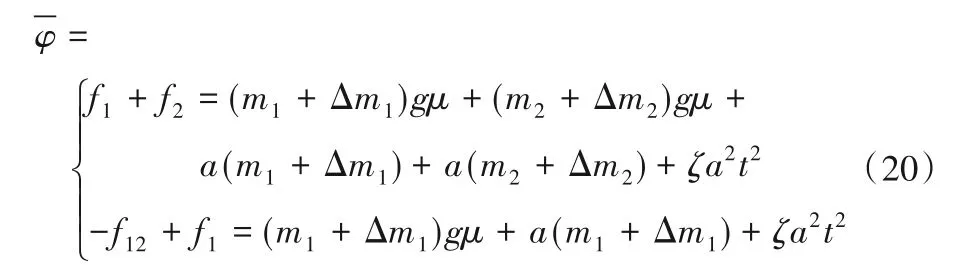
由第3章的推理方法的步骤2得式(21):
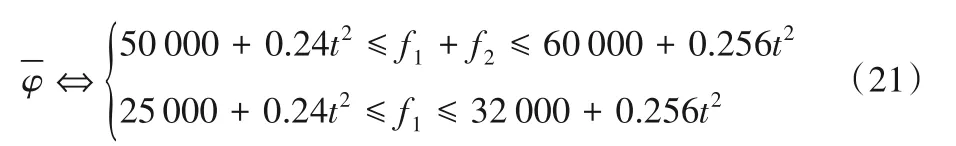

图2 的空间区域Fig.2 Spatial region of Zero(-φ)
4.2 模拟与测试
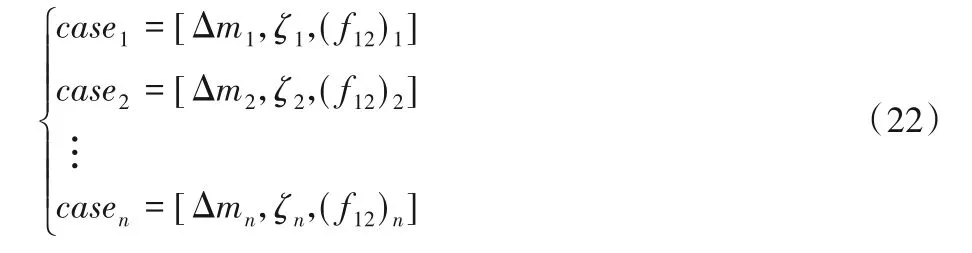
将式(22)代入式(20),可得到n个解,表示如式(23):
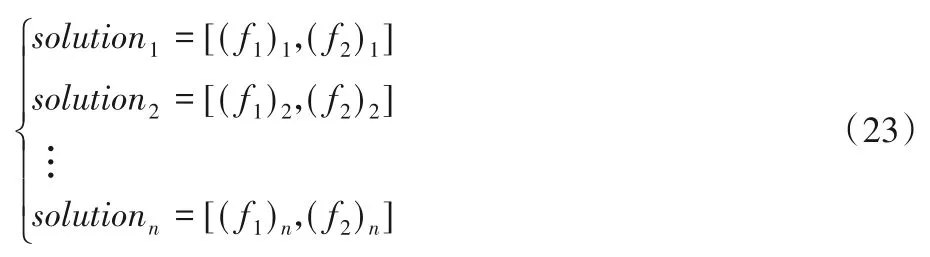
将式(23)中的n个解分别代入式(21),来验证是否满足该不等式组。分别测试了n=1 000,n=10 000,n=100 000的情况。其中图3和图4为1 000个解的空间位置(n=1000)。图5为10 000个解的空间位置(n=10 000)。图6为100 000个解的空间位置(n=100 000)。
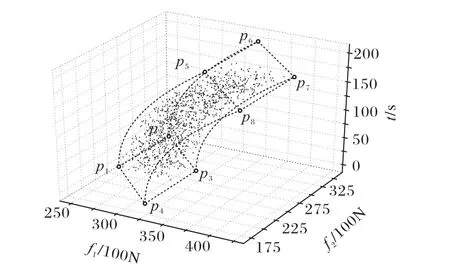
图3 1 000个测试用例Fig.3 A thousand test cases
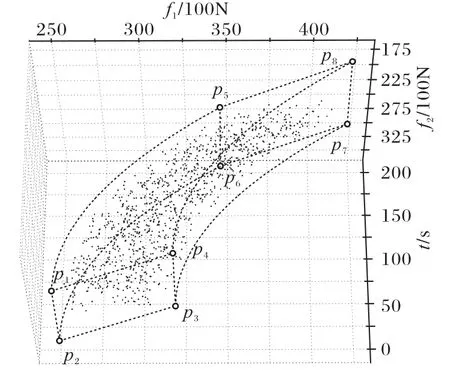
图4 图3的另一角度Fig.4 Another angleof Fig.3

图5 10 000个测试用例Fig.5 Ten thousand test cases
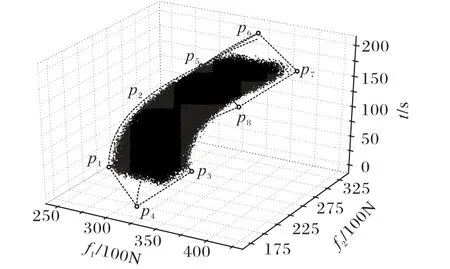
图6 100 000个测试用例Fig.6 Onehundred thousand test cases
经测试,所有的解都在式(21)表示的区域内。这个区域表示由不确定误差系数导致的可能的动力分配区域,以保证列车平稳加速行驶。如果列车平稳加速过程中的动力分配不在这个区域内部,或始终接近该区域的边界时,则表示存在非误差因素对动力系统的影响。这时需要排除是否存在机械故障,比如车轴轴承或电机轴承是否需要更换润滑脂。
4.3 推理分析
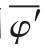

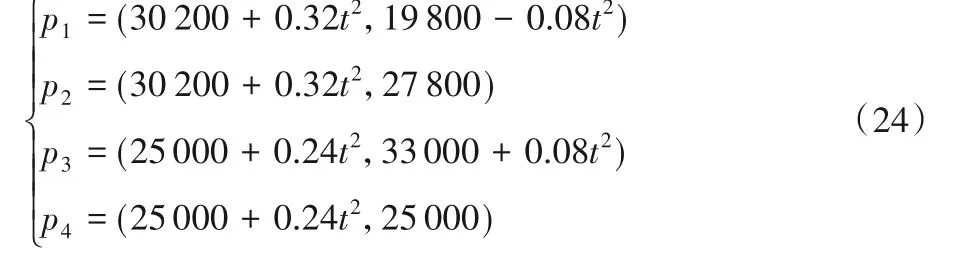
其中t∈[0,200]。
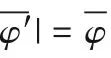
5 结语
对于系数和变量有误差的系统,大多数以前的推理方法都不适用。但是文献[18]方法对具有单个误差变量的多项式系统有非常高的理论价值。在多个误差变量的推理方法上,已有的文献还少有报道。另一方面,针对误差的模糊推理[19]也有一些学者在研究,这类方法最终给出了推理结论正确性的模糊程度或类似结论,这与本文提出的推理方法是有区别的,本文的推理方法最终可以给出推理结论是否正确的确定性回答。
本文推理方法可对给定误差区间的线性断言进行可靠的推理。此外,对于那些零点不完全非负的线性误差断言,可用变量替换将其零点全部做非负处理。例如,摄氏温度c是有可能出现负值的,可以用一个变量替换c'=c+273.15,其中c'表示其相应的开尔文温度(绝对温度)。然而,在非线性误差多项式断言的推理方法上,目前仍没有有效的解决方法。结合控制点生成方法,有望将非线性误差多项式断言的零点集作线性化包含处理,这样可以进一步扩大该方法应用范围,这也是今后的工作方向。

