基于弹性势能的多模数直齿轮副接触应力分析

朱增宝 龚明针 王东雨

摘 要：为了研究模数变化对多模数渐开线直齿轮副齿面接触应力的影响规律，根据理论齿侧间隙为零原则，推导了多模数渐开线直齿轮副的啮合角计算公式;引入了渐开线齿廓参数，结合基于最小弹性势能的非均匀载荷分配模型和赫兹应力模型，提出了多模数直齿轮副齿面接触应力计算公式并对多模数渐开线直齿轮副接触应力进行分析。结果表明：齿面接触应力随模数比增大而减小;采用多模数啮合形式，能减小少齿数主动轮啮合起始点的接触应力;齿面最大接触应力位置在啮合起始点或单齿啮合内点。

关键词：多模数;渐开线直齿轮副;载荷分配;接触应力

Abstract：In order to study the effect of modulus change on the contact stress of multi-module involute spur gear pair，the formula was derived for calculating the meshing angle of the involute spur gear pair with multi-module based on the theory that the tooth side clearance was zero. By introducing the involute tooth profile parameters and applying the non-uniform load distribution model based on the minimum elastic potential energy and the Hertz stress model， a formula for calculating the contact stress on the tooth surface of the multi-module spur gear pair is presented and the contact stress of the multi-module spur gear pair is analyzed. The results show that the contact stress decreases with the increase of modulus ratio. Adopting multi-module meshing can reduce the contact stress of the initial meshing point of the driving wheel with few teeth. The position of the maximum contact stress of tooth surface is the initial meshing point or the inner point of single tooth meshing.

Key words：multi-module;involute spur gear pair; load distribution; contact stress

渐开线齿轮广泛应用于航空航天、船舶车辆和工程机械等领域，齿面接触应力是影响其接触疲劳破坏的主要因素[1]，同时也是衡量与评估齿面接触承载能力的重要条件。文献[2-3]使用赫兹接触理论来评估接触应力，假定载荷沿接触线均匀分配，并引入了几种载荷分配影响因素来校正接触应力的计算值[4-5]6。实际上，载荷分布取决于齿轮副接触点的啮合刚度，刚度在任何接触点都不同，这意味着每单位齿宽的载荷在接触线的任何点上也都不同[6]。有许多研究通过理论计算法、实验和有限元分析等多种方法确定了直齿轮副的载荷分配比[7-10]785。

以上研究都是针对主、从动轮模数相等的齿轮副。对于主、从动轮模数不相等，但满足法节相等啮合条件的齿轮副（简称多模数齿轮副）的齿面接触应力研究，目前鲜见相关报道。

基于此，本文根据理论齿侧间隙为零原则，推导了多模数渐开线直齿轮副的啮合角计算公式。引入渐开线齿廓参数，结合赫兹理论模型和基于最小弹性势能的载荷分配模型，推导多模数齿轮副的齿面接触应力公式;分析了模数比对多模数齿轮副接触应力的影响，为多模数啮合齿轮传动设计提供参考。

1 多模数直齿轮副无侧隙啮合方程

1.1 齿轮副正确啮合条件

渐开線直齿轮正确啮合条件[11]

1.2 齿轮副无侧隙啮合方程

在无侧隙啮合情况下，主动轮沿节圆的齿厚sH1等于从动轮沿节圆的齿槽宽度wH2。

2 载荷分配模型

2.1 齿廓参数

文献[7]782详细介绍了最小弹性势能的载荷分配模型。弹性势能是根据弹性理论和齿轮齿形参数计算得出，单位载荷和单位齿宽的势能（单位势u）取决于接触点，主动轮齿廓上的接触点齿廓参数ξ为式中：z1为主动轮齿数;rb1为主动轮基圆半径，mm;rC1为主动轮在接触点处的半径，mm。该参数具有物理意义：它是接触点处的曲率半径与基圆齿距之比，也是接触点的滚动角与齿距圆心角2π/z之比。

2.2 载荷分配

在考虑同时接触的所有成对齿的情况下计算弹性势能，其中作用在每对齿上的负载计算公式由文献[7]784得

3 多模数直齿轮接触应力计算公式推导

3.1 赫兹公式

3.2 多模数直齿轮副接触应力公式推导

以赫兹公式为基础推导适应多模数渐开线直齿轮副啮合特点的齿面接触应力计算公式，过程如下。

4 多模数齿轮副齿面接触应力分析

4.1 算例参数设置

本文渐开线齿轮材料：齿轮的材料为20CrMnTi，表面渗碳淬火处理，齿面硬度HRC 57～63，弹性模量E为206GPa，泊松比ν为0.3。齿轮副基本参数设置如表 1所示。

由式（1）易知，从动轮的分度圆压力角α2随着模数比的增大而增大，易出现齿顶变薄、加载时容易断齿的现象[15]。根据文献[16]可知，工程实际应用齿厚通常要大于0.25～0.4倍的模数，本文中取模数比时均以0.25倍模数为最小齿厚限制，因此本文模数比上限可取到1.08～1.1。为使从动轮的分度圆压力角不小于20°，本文中模数比下限取为1.0。

4.2 主动轮齿数较少时齿面接触应力分析

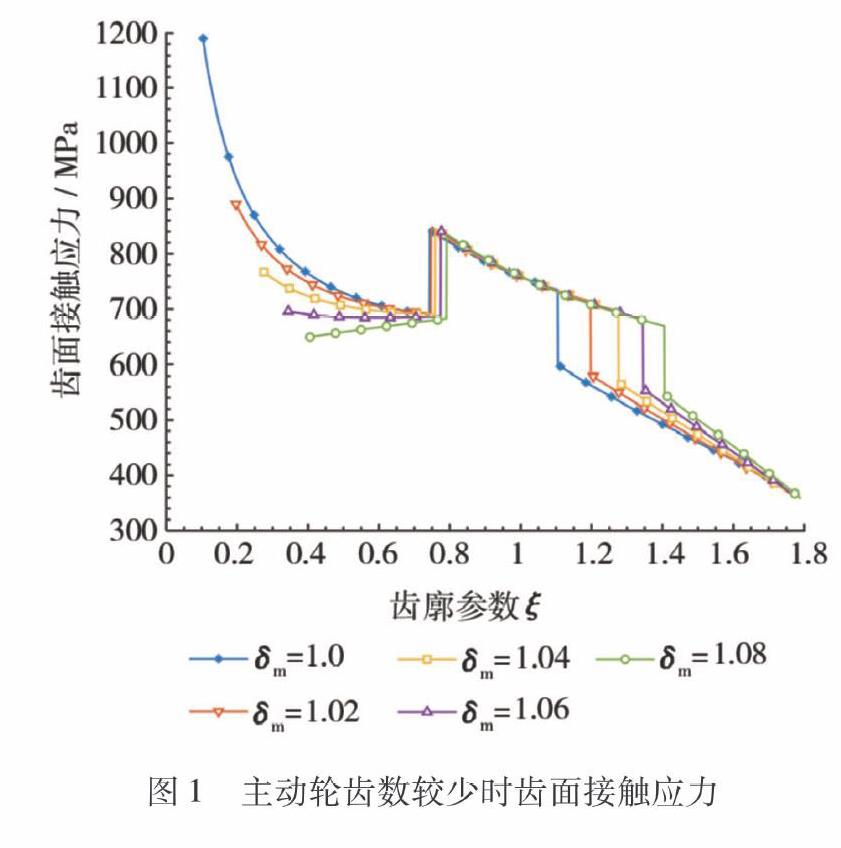
现以主动轮转数为4 000r/min， 传输功率为150kW， 主动轮齿数为17， 从动轮齿数为52的齿轮副带入式（26）取模数比分别为1.0、1.02、1.04、1.06、1.08进行齿面接触应力计算，得到各模数比的齿面接触应力情况如图1所示。

由图1，当齿轮副齿数比较大且主动轮轮齿较少时，齿面接触应力的最大值并没有出现在单齿啮合内点附近，而是出现在啮合起始点。因此，并不能将单齿啮合内点的齿面接触应力计为最大值，而应比较单齿啮合内点和啮合起始点处应力值的大小。

对于啮合起始点附近的齿面接触应力会异常大的现象，本文从综合曲率半径的角度来说明。由式（22）可知，当齿廓参数值ξinn非常小时综合曲率半径ρΣ（ξ）值较小，从而通过计算得到的齿面接触应力较大。从图1可以看到，模数比的改变正是增大了ξinn才使得小齿数齿轮啮合起始点的齿面接触应力减小。因此，采取多模数啮合形式用于齿轮副齿数比较大且主动轮轮齿较少的情况可以有效的减小啮合起始点的应力。

4.3 主动轮齿数较大时齿面接触应力分析

现以主动轮转数为4 500r/min，传输功率为450kW，主动轮齿数为29， 从动轮齿数为101的齿轮副带入式（26）取模数比分别为1.0、 1.02、 1.04、1.06、1.08、1.1进行齿面接触应力计算，得到各模数比的齿面接触应力情况如图2所示。

对比主动轮齿数较少时的情况可以发现：当主动轮齿数较多时，齿面接触应力较大的点出现在单齿啮合内点;随着模数比的增大，啮合起始点的接触应力有较大幅度的降低，这也要得益于增大了模数比的缘故。因为，模数比的增大使得啮合起始点齿廓参数值ξinn增大，增大了该点的综合曲率半径，从而降低了齿面接触应力。

4.4 节点的接触位置和接触应力分析

通过对主动轮节圆半径的计算，利用式（6）很容易得到节点在接触线上的位置，也很容易计算节点所在位置的接触应力。本文发现，当模数比处于某一范围时，多模数齿轮副节点会处于双齿啮合区，如图2圆点标示。通过计算单齿啮合区外点齿廓参数ξout和节点齿廓参数ξp，可以发现，当模数比δm≥1.014 3时有ξp≥ξout=ξinn+1，也就是说节点已经处于双齿啮合区了。齿轮副参数（如齿数）会影响多模数齿轮副节点位于双齿啮合区的临界模数比值，例如主动轮齿数为17，从动轮齿数为52时，在没有变位的条件下，只有当δm≥1.068 7时，节点才能处于双齿啮合区。

如图2圆点标示，当模数比δm=1.0时—齿轮副节点位于单齿啮合区—节点附近为单对齿受力，接触应力值约为700MPa。当模数比δm分别为1.02、1.04、1.06、1.08、1.1时—齿轮副节点位于双齿啮合区—节点附近为两对齿受力;随着模数比的增大节点应力降低得非常明显，当模数比δm=1.1时，节点接触应力值小到400MPa以下，节点的接触应力变化量为48.6%。

对于使用最多的压力角为20° 的渐开线非变位同模数直齿轮副来说，在节圆附近只有一对齿啮合，节点附近的齿面承受了全部載荷。在绝大多数情况下齿轮的点蚀发生在节圆附近的齿面上。因此，若节点位于两对齿啮合区内，减小易产生点蚀部分的载荷，点蚀便不易产生。从这一角度考虑，本文改变齿轮副模数比使节点位于双齿啮合区的啮合传动方法是有益的。

5 模数比对最大齿面接触应力的影响

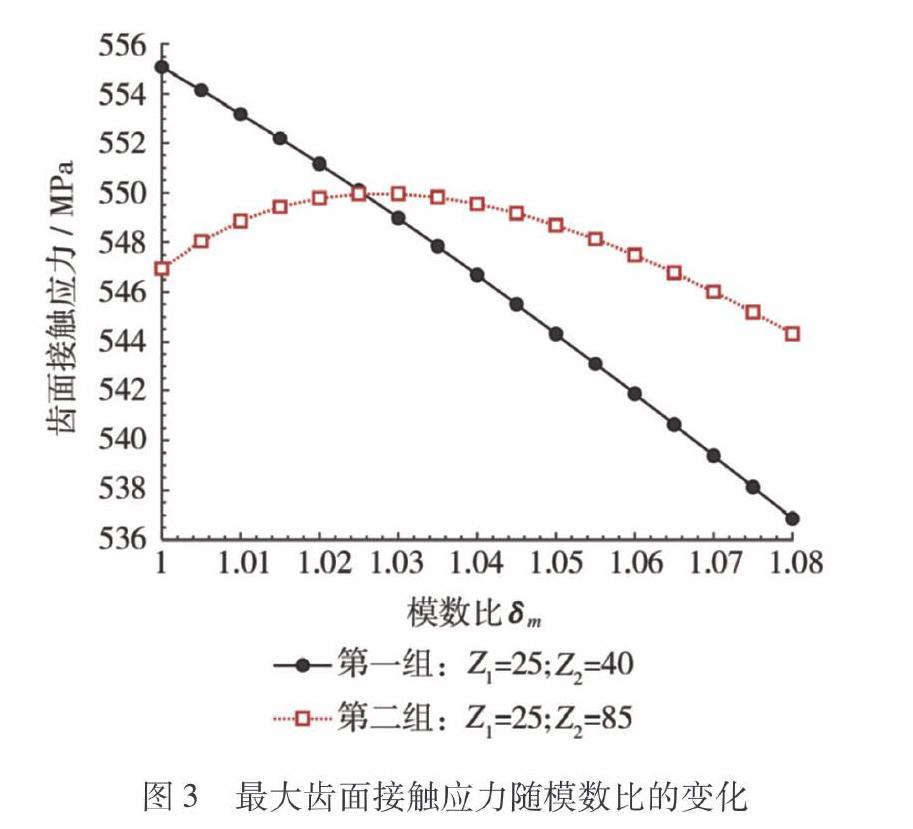
在实际齿面强度的校核计算中，最关心的还是沿接触线的最大齿面接触应力。为找到模数比对最大齿面接触应力的具体影响，先后对下列两组齿轮副：第一组：z1=25， z2=40; 第二组：z1=25，z2=85进行不同模数比下的最大齿面接触应力计算，结果如图3所示。需要说明的是图3两组齿轮副的传递功率有所不同，但是这并不影响其变化趋势。

由图3可以看出，在第一组齿数条件下，随着模数比的增大，齿轮副最大齿面接触应力有所降低而且是持续降低。在第二组齿数条件下，最大齿面接触应力有一个先增后减的趋势;当模数比δm=1.03时达到最大，δm=1.08时达到最小。结合图2和图3可知，模数比改变了齿轮副齿形参数，随之改变的是齿廓参数，从而改善最大齿面接触应力。单从齿面接触应力这一点来说，模数比越大接触应力总体有降低的趋势。

6 结论

（1）渐开线直齿轮齿面接触应力较大的位置不总是出现在单齿啮合内点附近;当齿轮副齿数比较大且主动轮轮齿较少时，齿面接触应力较大的位置便出现在啮合起始点附近。

（2）当齿轮副齿数比较大且主动轮轮齿较少时，主动轮齿根附近的接触应力会异常的大，若采取多模数啮合形式增大啮合起始点综合曲率半径从而减小了该点接触应力。

（3）多模数直齿轮副可以通过改变齿轮副模数比使节点位于双齿啮合区，从而使节点附近承受的接触压力显著降低。

（4）在一定的齿数条件下，齿轮副最大齿面接触应力随着模数比的增大而有所减小。在齿轮系统设计中采取多模数啮合形式可改善接触应力。

参考文献：

[1] 朱有利，王燕礼，边飞龙，等.渐开线直齿圆柱齿轮接触疲劳失效成因再分析[J].摩擦学学报，2014，34（6）：722-728.

[2] ISO Standard 6336.Calculation of load capacity of spur and helical gears：Calculation of surface durability[S].International Organization for Standardization：Geneva，Switz-erland，1996.

[3] ISO Standard 6336.Calculation of load capacity of spur and helical gears：Basic Principles，Introduction and General Influence Factors[S].International Organization for Standardi-zation：Geneva，Switzerland，1996.

[4] GB/T 3480.渐开线圆柱齿轮承载能力计算方法[S].中国：国家标准局，1997.

[5] AGMA Standard.Fundamental rating factors and calculation methods for involute spur and helical gear teeth[S].American Gear Manufacturers Association：Alexandria，VA，2004.

[6] SANCHEZ M，PLEGUEZUELOS M，PEDRERO J.Approximate equations for the meshing stiffness and the load sharing ratio of spur gears including hertzian effects[J].Mechanism and Machine Theory，2017，109（1）：231-249.

[7] PEDRERO J，PLEGUEZUELOS M，ARTES M，et al.Load distribution model along the line of contact for involute external gears[J].Mechanism and Machine Theory，2010，45（5）：782-789.

[8] RISTIVOJEVIC M， LAZOVIC T， VENCL A.Studying the load carrying capacity of spur gear tooth flanks[J].Mechanism and Machine Theory，2013，59（1）：125-137.

[9] SPITAS V，PAPADOPOULOS A，SPITAS C，et al.Experimental investingation of load sharing in multiple gear tooth contact using the stress optical method of caustics[J].Strain，2009，47（4）：227-233.

[10] LI S.Effect of addendum on contact strength，bending strength and basic performance parameters of a pair of spur gears[J].Mechanism and Machine Theory，2008，43（12）：1 557-1 584.

[11] 仙波正庄.齿轮变位[M].上海：上海科学技术出版社，1984：244-254.

[12] Φ JI 李特文.齿轮啮合原理[M].上海：上海科学技术出版社，1984：194-195.

[13] 叶福民.非等模数非等压力角行星齿轮传动系统设计与动力学特性研究[D].南京：南京航空航天大学机电学院，2014：10-20.

[14] 叶福民，朱如鹏，鲍和云.非等模数非等压力角NGW型行星齿轮系几何尺寸研究[J].机械科学与技术，2011，30（5）：732-735.

[15] 肖望强.非对称齿廓齿轮彎曲疲劳强度理论分析与试验[J].机械工程学报，2008，44（10）：44-50.

[16] 朱景梓，张展，张焕武，等.渐开线齿轮变位系数的选择[M].北京：人民教育出版社，1981：68-69.