基于随机环境下的物流网络流量分配研究

都晓惠 孟凡锋

摘 要：物流网络流量合理分配，对网络成本的降低具有重要意义。传统基于确定性条件下的物流网络流量分配问题无法准确反映出网络的动态变化，因此本文提出考虑随机环境下的物流网络配流模型，以使得研究结果更加符合实际情况。运用区间数表达网络中的不确定因素，构建以网络运输总成本最小为目标的优化模型，根据求解结果分析物流网络合理性。最后通过算例验证了模型的有效性。研究表明：区间规划可以有效处理随机环境下的物流网络流量分配问题，具有实际应用价值。

关键词：物流网络;随机环境;区间数;配流模型

随着贸易全球化的发展，物流网络作为货物流动的载体扮演着越来越重要的角色。因区域经济或环境的影响，物流网络中的网络要素并非静态，而是具有一定的随机性。因此，如何合理考虑网络中的不确定因素，使得所构建网络更加符合现实情况受到大家广泛关注。

Wang[1]等根据网络实际情况和现实条件进行适当假设，研究网络配流问题;Lin YK[2]以运输时间作为衡量路径长度的标准，对物流网络展开研究;周晓[3]结合决策者偏好，构建层次变权的物流网络;韩世莲[4]等提出物流网络的多目标最短路问题;范厚明[5]通过设定需求情景表达不确定需求，研究中转站选址问题;李淑霞[6]等采用两阶段随机规划方法完成物流网络中转点选址及路径规划;邹高祥[7]等引入三角模糊数理论研究客户需求不确定的网络优化问题;Emrah Demir[8]等考虑需求和速度的不确定性，利用SAA算法为物流网络设计运输方案。

区间规划方法于1965年被 Moore 提出，该方法无需较多的先验知识和假设条件，本文选用区间规划处理物流网络中的不确定因素。物流网络中，节点的运输需求受众多因素影响，因此具有不确定性;路段可用运载工具数量因车辆调动、天气及日常维修保养等原因具有随机性。因此，本研究综合考虑网络中需求不确定性及路段运能的不确定性，目的使得所构建网络可代表实际网络中的多数情况。

1模型构建

1.1问题描述

物流网络由节点和弧组成，节点包括供应节点、配送中心和需求节点三类，弧是指将不同节点连接起来的运输路径。考虑网络中的不确定要素，包括需求的不确定性和路段运能的不确定性，目的是使得优化结果具有较强的鲁棒性。在此基础上构建流量分配模型，根据配流结果分析现有网络的运营水平及存在的问题。

本文运用区间数代替一个确定的值，节点需求量及路段的可用车辆数均为区间数。需求节点的需求量区间已知，供应节点供应量充足，研究如何合理分配货流，使得物流网络总成本最小。

1.2模型假设

（1）只考虑一种货物;

（2）同类节点之间不发生货物流动;

（3）供应节点供应量充足。

1.3参数设定

1.3.1集合

供应节点集合;配送中心集合;需求节点集合;，为一个区间数，为区间下限，为区间上限。

1.3.2参数

供应节点编号;配送中心编号;需求节点编号;需求节点i的需求量，为一个区间数;配送中心容量限制;配送中心操作成本;从起点i到终点j的单位运输成本;从起点i到终点j的可用车辆数;运载工具的单位运量。

1.3.3决策变量

从起点i运到终点j的运量区间;

1.4模型构建

目标函数（1）表示从供应节点到需求节点的成本之和，包括从供应节点到配送中心的运输成本，配送中心到需求节点的运输成本以及配送中心的操作成本;（2）表示需求节点需求量得到满足;（3）表示配送中心流量守恒;（4）表示到配送中心的货物总量不超过配送中心最大容量;（5）-（6）为不同路段的运能约束;（7）为决策变量约束。

1.5模型的确定性转化

因区间数无法直接进行比较和计算，需要将区间线性规划模型转化为确定性线性規划模型求解。郭均鹏[9]等在《区间线性规划的标准型及其求解》一文中，为区间线性规划提供了解决方案。现假设存在区间线性规划问题：

2算例分析

2.1数据收集

在一个物流网络中，包括2个供应节点A1-2，3个配送中心B1-3和9个需求节点C1-9。供应节点可为任意需求节点提供服务，找到一种运输方案使得该网络中运输成本最小。模型中节点需求区间、配送中心容量、运输成本及配送中心操作成本、运能上下限已知，给定：=0.6，。设计遗传算法求解算例。

2.2结果分析

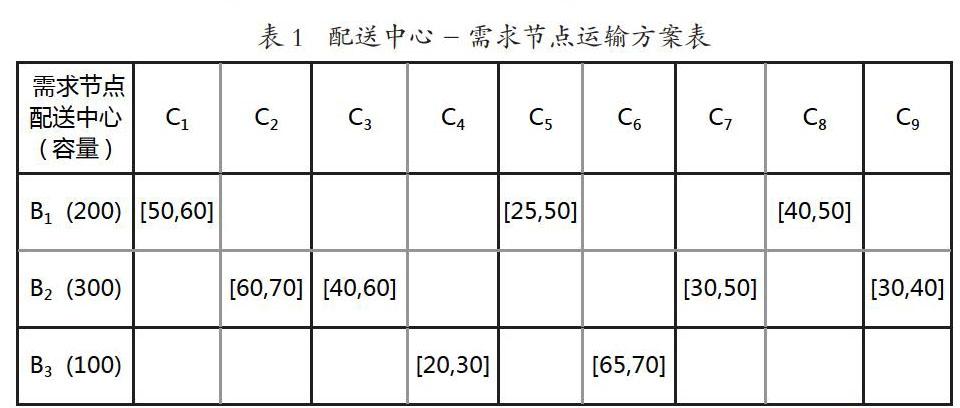
结果表明：供应节点A1与配送节点B3间有货物流动，供应节点A2与配送中心B1和B2有货物流动。配送中心与需求节点间的货物流动情况如表1所示：

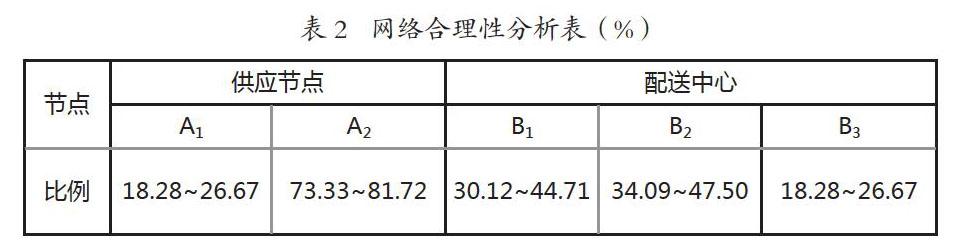
以B1-C1为例解释表1，需求节点C1的需求量区间为[50，60]，由配送中心B1配送，配送中心B1由供应节点A2供应，综上需求节点C1的运输方案为A2-B1-C1。根据运输方案，可确定各节点货流所占比例，得网络合理性分析表如表2所示：

表2可看出，供应节点A2 的货流比例明显高于A1，配送中心B3 货流分配比例低于其他两个配送中心，物流网络中货流分配不均衡。可通过改进网络要素使网络配流均衡，从而提高整个物流网络的运营效率，为进一步优化网络提供理论方向。

3结论

本研究 针对物流网络配流问题，首先分析网络中存在的不确定要素，包括需求节点需求的不确定性，运能的不确定性。用区间数代替确定的值表达不确定性，充分考虑了网络中可能发生的不同情况。结果表明：区间规划方法适用于物流网络配流问题中，可以为供应商提供较优的运输方案;同时根据配流结果可以发现现有网络中存在的问题，为进一步优化网络提供了决策支持。

参考文献：

[1] Wang Qingbin，Zang Baige.Optimal Model for the Distribution of the Cargoes in Inland Collection and Distribution Network of the Port.ICISE2009，The 1st International Conference on Information Science and Engineering.EI：20102212965213.

[2] Lin YK. Time version of the shortest path problem in a stochastic-flow network[J].  Journal of Computational and Applied Mathematics， 2009（1）：150-157.

[3]周晓.基于层次变权的物流网络流量分配模型[J].山东农业大学学报（自然科学版），2017，48（06）：943-947.

[4]韩世莲，刘新旺等.物流运输网络多目标最短路问题的模糊满意解[J].运筹与管理，2014（5）：55-61.

[5]范厚明，李彩云，蒋晓丹，徐振林.不确定需求下考虑路径可靠性的内陆港选址问题[J].管理学报，2018，15（08）：1256-1264.

[6]李淑霞，陈振，刘丽萍，吴一帆，孙思凡.基于不确定需求的多式联运物流网络设计[J].东华大学学报（自然科学版），2018，44（04）：550-554+577.

[7]邹高祥，杨斌，朱小林.考虑模糊需求的低碳多式联运运作优化[J].计算机应用与软件，2018，35（10）：94-99.

[8] Emrah Demir.A green intermodal service network design problem with travel time uncertainty[J].Transportation Research Part B：Methodological，Volume 93，part B，November 2016，Pages 789-807.

[9]郭均鹏，吴育华.区间线性规划的标准型及其求解[J].系统工程，2003（03）：79-82.