基于约束模型的多目标柔性作业车间调度问题求解
罗 雄,钱 谦,伏云发,冯 勇
(1.昆明理工大学信息工程与自动化学院,云南 昆明 650500;2.昆明理工大学云南省计算机技术应用重点实验室,云南 昆明 650500)
0 引言
柔性作业车间调度问题( flexible job-shop scheduling problem,FJSP)是作业车间调度问题(jobshop scheduling problem,JSP)的扩展,是计算复杂度更高的NP 难问题。 多目标柔性作业车间调度问题
(multi-objective flexible job-shop scheduling problem,MOFJSP)是FJSP 的子问题。 由于该问题更贴近实际的生产活动,对其进行研究可以更好地为企业经营者决策提供支持。 在实际生产活动中,MOFJSP 各个优化目标的相互冲突,导致MOFJSP 与单目标的FJSP、JSP 有着本质的区别,即一般情况下,多目标优化的最优解不是唯一的[1]。
在现阶段使用遗传算法求解MOFJSP 的研究中,朱伟[2]基于基础模型,考虑了工件移动时间的约束,建立了包括最小化最大完工时间、最小化总加工成本在内的多目标组合优化模型,并改进遗传算法中的变异算子自适应变异规则,求解MOFJSP。 王雷[3]等建立以完工时间、机器能耗和工人操作机器的舒适度为优化目标的优化模型,并使用改进的遗传算法进行求解。Fattahi[4]考虑了机器与工件的动态插入调度,建立了多目标优化的动态调度模型,并使用遗传算法进行求解。 张国辉[5]等构建了低碳多目标调度模型,使用改进的遗传算法对有低碳需求的车间进行求解。 以上研究均使用加权求和法将多个优化目标进行加权求和,从而转化为单目标进行求解。 虽然该方法易操作、易实现,但每次只能获得一个解,且权重设置的不同会导致输出结果的严重差异。 因此,如何保证产生多个调度方案供选以及尽可能地靠近最优解,是使用遗传算法求解MOFJSP 所需解决的问题之一。 极大极小法[6]是求解多目标优化的方法之一,被广泛运用于机械设计[7]中。 其主要思想是:若优化问题的某一目标可以给出一个可供选择的范围,则该目标就可以作为约束条件,从而被排除出目标组,进入约束组。 因此,该方法也被称为约束模型方法。 与加权求和法相比,该方法更为简单,并且能够在无需人为设置权重的情况下,产生多个调度方案供选。
本文基于极大极小法,对调度模型的优化目标作约束化处理,并以改进的遗传算法求解MOFJSP。 具体操作如下:使用余弦相似度计算个体间的相似程度,避免算法在运算过程中丢失种群的多样性从而陷入局部最优;改进基于机器编码的交叉操作及基于工序编码的变异操作,避免算法在运算过程中产生非法解,从而对上述两种算子作有效性验证;最后,建立以最小化最大完工时间和最小化碳排放量为优化目标的多目标调度模型,以改进后的遗传算法对MOFJSP 的实例进行仿真运算,验证算法的性能及方法的可行性。
1 问题描述及数学模型
1.1 柔性作业车间调度问题描述
柔性作业车间调度问题通常分为完全柔性作业车间调度问题(T-FJSP)和部分柔性作业车间调度问题(P-FJSP)。 由于P-FJSP 更贴近实际的生产活动,其研究较多,一般描述如下:对于给定的一个待加工工件集合与机器集合,每个工件包含多道工序,且有特定的加工顺序;允许工序在任意台可用机器上进行加工,且加工时间确定;若不单独指明柔性,一般默认为具有机器柔性的作业车间调度问题。 部分柔性作业车间调度问题实例如表1 所示。
表1 中,N 表示该机器无法对当前工序进行加工。如O23表示第2 个工件J2的第3 道工序,可选机器集为{M1,M2,M3,M4}。M5为不可选机器,无法对O23工序进行加工。 如果选择第1 台机器,则O23工序使用第1 台机器进行加工的时间长度为1。
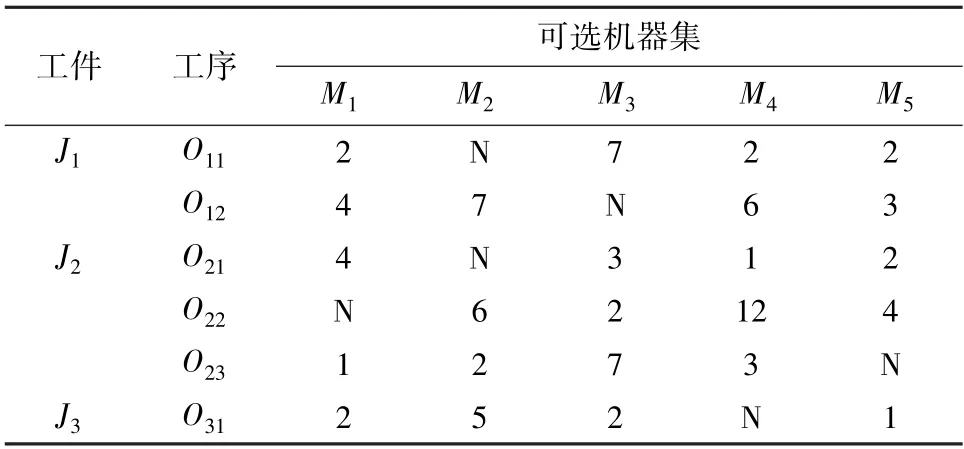
表1 部分柔性作业车间调度问题实例Tab.1 Example of partially flexible job-shop scheduling problems
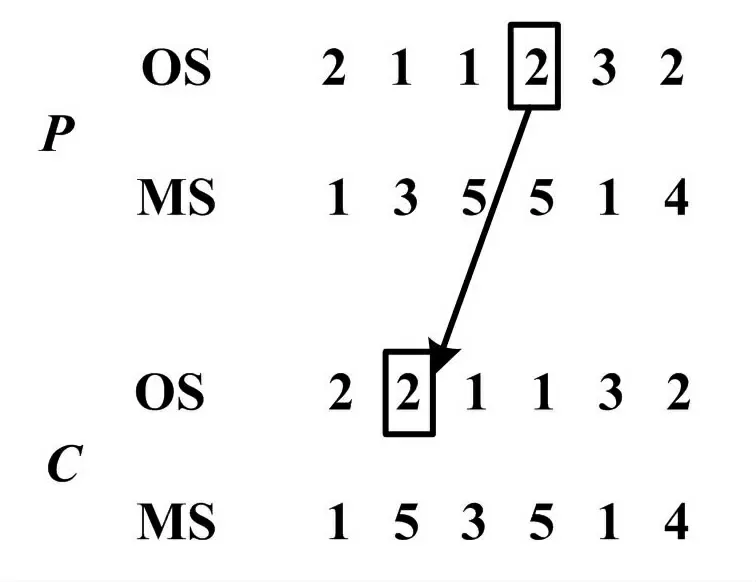
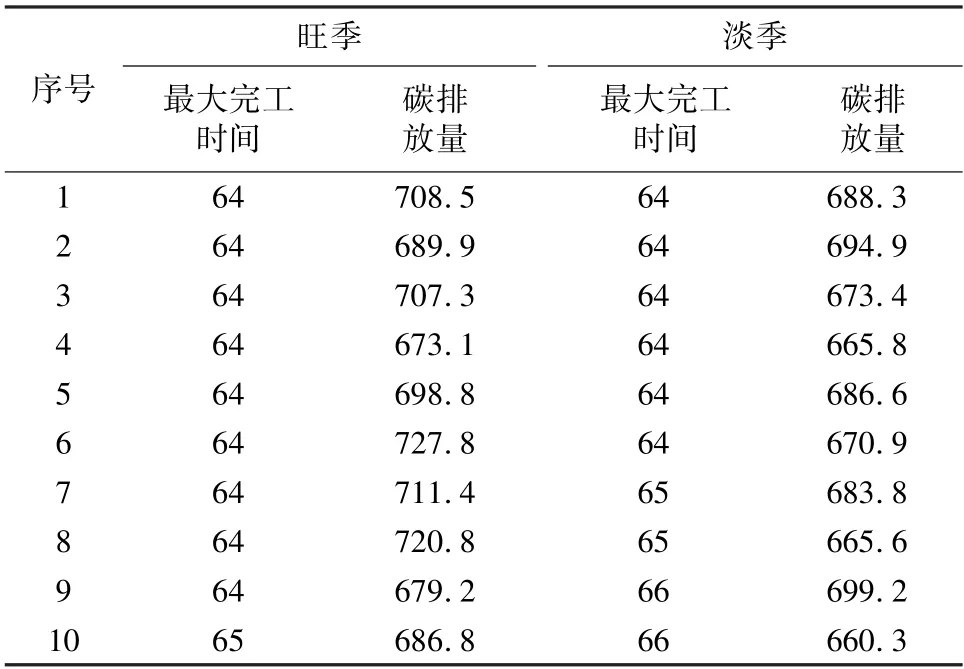
其约束条件如下。 ①令J={Ji},1 在实际的生产活动中,优化问题一般都是多目标优化问题[8],如生产效率、生产成本和设备的利用率等。 这些都是企业普遍关心的问题。 因此,根据优化目标的不同,建立调度模型如下: 式中:f1为基于最大完工时间的指标,表示生产效率的高低;Gi为完成第i个工件所用时间;n为工件总数;f2与f3为基于设备负荷的指标,表示设备利用率;Tijk为工件i的第j道工序在机器Mk上的加工时间;ni为其工序总数;f4与f5为基于拖期的指标,表示交货性能的强弱;Ei为工件i的交货期时间di与工件i的完工时间Gj的非负差值,Ei=max(di-Gi,0),即工件i的提前完工时间;ΔTi为工件i的完工时间Gi与工件i的交货期时间di的非负差值;Ti=max(Gi-di,0),即工件i的拖期时间;f6为基于节能减排类的指标,表示生产成本或碳排放量等成本类指标;ei为单位时间内的碳排放量或生产成本。 本文采用双层编码方式对染色体进行编码:每条染色体由工序编码OS 和机器编码MS 组成。 其中:工序编码OS 为随机编码,即随机产生工序序列;MS 按照已产生的工序顺序OS,依次从可选机器集中随机选择可用机器作为MS 的编码。 根据表1 所描述的FJSP,随机产生的一条染色体结构如图1 所示。 图1 一条染色体结构示意图Fig.1 Schematic diagram of a chromosome structure 解码时,工序编码和机器编码一一对应,只需要从左至右依次遍历OS,根据表1 所示的时间表产生一个可行解,即一个合法的生产调度方案。 个体的相似度用于衡量个体之间的相似程度,一般通过计算个体在特征空间中的距离获得。 在使用遗传算法的个体相似度计算中,一般将每条染色体作为一个特征向量,使用海明距离[9]计算个体等位基因的相同基因个数,从而得到两条染色体之间的相似度。但该方法针对一些与问题密切相关的编码方式时并不适用[9]。 例如,该方法并不适用或很难适用于MOFJSP。 因此,本文引入余弦相似度[10]对个体进行相似度区分。 由上述编码方式,可将每条染色体作为一个多维向量,通过计算每一对个体的夹角余弦值得到个体相似度后,再确定其是否进行交叉操作或进行变异操作。 其公式如下: 式中:xi、yi为即将交叉的2 个个体;cosθ的取值范围为[0,1]。 由式(1)可知,余弦值越大,夹角越小,说明2 个个体间的相似度越高。 使用遗传算法求解MOFJSP 的交叉操作分为两部分。 第一部分为基于工序编码OS 的交叉操作。第二部分为基于机器编码MS 的交叉操作。 在常用基于机器编码MS 的互换交叉方式[11]中,机器编码的随机互换易导致工序所对应的机器编码MS 失效。针对上述缺陷,本文对该方式进行改进,使之不会产生非法解。 改进后的互换交叉如图2 所示。 图2 改进后的互换交叉示意图Fig.2 Schematic diagram of improved crossover 针对工序编码OS 的交叉方式,本文使用IPOX[5]交叉方式。 ①在父代染色体P1中,产生2 个不大于染色体长度N的随机点X1、X2。 如图2 所示,产生随机点基因位2 和基因位4。 ②在P2中搜索P1位于随机点X1和X2之间的所有对应工序,用P2中对应工序的对应机器替换P1位于随机点X1和X2之间的机器。 如图2 所示,在P2中搜索工序O21、O12和O22,将P2中的机器编码3、2、4 替换P1中的机器编码1、5、5。 保持父代P1和P2的顺序,从而得到两个交叉后的子代C1和C2。 使用遗传算法求解MOFJSP 的变异操作也分为两部分。 第一部分为基于工序编码OS 的变异操作。 第二部分为基于机器编码MS 的变异操作。 基于工序编码OS 的常用插入变异[3]方式中,工序的随机插入不但改变了同一工件的工序顺序,同时也改变了工序所对应机器的编码顺序,导致第二层机器编码MS 失效。针对上述缺陷,本文对该操作进行改进,使之不会产生非法解。 改进后的插入变异如图3 所示。 针对机器编码MS 的变异方式,本文使用常见的单点变异方式[5]。①在工序编码OS 中,产生一个不大于染色体长度N的随机点X1。 图3 产生随机点基因位4。 ②同时,往左、往右搜索,遇到相同工件,则停止。 如图3 所示,随机点X1为工件2,往左搜索至基因位2 为止,往右搜索至基因位5 为止。 则工序O22的可插入位置为S={基因位2,基因位3,基因位4,基因位5}。 ③产生一个在S内的随机点X2,将随机点X1的双层编码同时插入到随机点X2。 如图3 所示,随机点X2为基因位2 位置。 图3 改进后的插入变异示意图Fig.3 Schematic diagram of improved insertion mutation 为了验证改进后的基于机器编码的互换交叉方式及基于工序编码的插入变异方式的有效性,现对上述交叉方式及变异方式计算交叉优秀解[12]和变异优秀解。 为了使结果尽量客观有效,设交叉概率Pc和变异概率Pm均为1,以Brandimarte[13]设计的MK01 为测试数据,以Visual Studio 2017 为仿真平台进行算子的有效性验证。 交叉优秀解指的是父代个体进行交叉之后,生成的子代个体的适应度值优于父代个体适应度值的数量比例。 交叉后,若交叉优秀解个数较多,说明交叉方式较优;若交叉优秀解个数较少,则交叉方式较差。 根据MK01 的数据,随机生成两条适应度值较高的染色体,以保证算法在寻找交叉优秀解的过程中有较高的上、下限。 随机生成的2 条染色体如图4 所示。 图4 随机生成的2 条染色体Fig.4 Two chromosomes out of random 图4 中,P1染色体适应度值为114,P2染色体适应度值为94。 现将P1和P2这2 条父代染色体使用改进前、后的互换交叉方式[12]分别进行10 000 次不相关对比交叉操作。 交叉操作试验结果如表2 所示。 表2 交叉操作试验结果Tab.2 Experimental results of crossover 由表2 可知,改进后的互换交叉方式的最大适应度值为122,最小适应度值为74,平均适应度值为101.923,方差为75.433 9。 改进后的互换交叉方式在平均适应度上仅比常用的互换交叉方式高1.727。 但改进后的互换交叉方式产生的子代个体总体方差较小,低于常用互换交叉方式7.842 3。 因此,改进后的互换交叉方式与常用的互换交叉方式相比,具有较高的稳定性。 改进后的互换交叉方式产生的子代交叉优秀解个数为7 043 个,而常用的互换交叉方式产生的子代交叉优秀解个数为6 520,因此,改进后的互换交叉方式与常用的互换交叉方式相比,在寻找交叉优秀解上具有一定优势。 同时,由于常用的互换交叉方式打乱了工件的工序顺序,且交叉时未绑定工序编码,导致交叉后的机器编码几乎全部失效,需要多次对交叉后的染色体基因位进行修复。 因此,非法基因位个数较多,为108 962 个,平均修复非法基因位所需时间为0.000 216 1。 当数据规模较大或迭代次数较多时,基因位修复时间较长。 验证基于工序的变异方式,首先根据MK01 的数据,随机生成一条染色体,如图4 中的P1染色体。 现将P1染色体使用改进后的插入变异方式与常用的插入变异方式、常用的互换变异方式进行10 000 次不相关对比变异操作。 变异操作试验结果如表3 所示。 表3 变异操作试验结果Tab.3 Experimental results of mutation 由表3 可知,改进后的插入变异方式的最大适应度值为126,最小适应度值为73,平均适应度值为113.083,方差为22.303 2。 改进后的插入变异方式与其余2 种变异方式相比,平均适应度有所降低,且在总体方差上,改进后的插入变异方式为22.303 2,远远低于其余2 种变异方式。 因此,改进后的插入变异方式与其余2 种变异方式相比,具有较高的稳定性。 改进后的插入变异方式产生的子代变异优秀解个数为8 272 个,改进前的插入变异方式与它在此性能上类似,优秀解个数为8 531 个,但互换变异方式的子代变异优秀解个数为7 844。 因此,插入变异方式与互换变异方式相比,在寻找变异优秀解上具有一定优势。 同时,由于以上2 种已有变异方式均打乱了工件的工序顺序,且变异时未绑定工序编码,导致变异后的机器编码几乎全部失效。 因此,非法基因位个数较多,需要多次对变异后的染色体基因位进行修复,从而增加了算法的运算时间。 由有效性验证可知,改进后的交叉及变异方式杜绝了算法在运行过程中的非法解,节省了算法的运行时间。 在实际生产环境中,工件的生产均基于车间生产管理人员的约束。 旺季生产需要较小的生产周期,将最大完工时间最小化作为主要优化目标,对碳排放量给定一个可供选择的范围,从而作为约束条件,进入约束条件组。 设定旺季生产中,碳排放量小于730,则有调度模型为:f1=Gmax=maxGi,i=1,2,…,n。 其约束条件为:ti(j+1)k-tijg>Tijk;Tijk>0;Sijk⊂{t|tijk 淡季生产与旺季生产类似,设定完工时间小于67,现采用上述改进遗传算法对此多目标优化问题进行求解,并使用文献[5]中的实例数据与方法进行对比。 相关参数设置如下:种群规模P=100;最大迭代次数t=300,阈值S=0.8。 为了检测调度方案的优劣,已知该文献所用数据的最小完工时间为64。 由于该算法一次运行可得到较多调度方案,现运行5 次,从中挑选出表现较佳的10 个调度方案供决策者进行决策。 可供选择的调度方案如表4 所示。 由表4 可知,旺季生产只考虑生产周期时,整体生产周期均较短,10 个最优调度方案中有9 个达到64,但整体碳排放量相对较高。 淡季生产只考虑碳排放量时,整体碳排放量较低,最小值为660.3,低于文献[5]中的677.4,但生产周期相对较长。 文献[5]使用的加权求和法的每次计算均需按经验设定权重。 该方法易影响子代个体基因的继承。 当完工时间权重较高时,调度方案的碳排放量较高,有关碳排放量的优秀基因易丢失;当碳排放量权重较高时,调度方案的完工时间较长,有关完工时间的优秀基因易丢失。 且该方法在每次计算后仅能得到一个调度结果,不利于企业经营者进行决策。 文中使用极大极小法,对基础模型进行约束。 该模型无需设定权重,使得算法在运行过程中,能够较好地继承优秀基因,从而较快地得到满意的调度方案,且产生多个调度方案供企业经营者进行决策。虽然未同时兼顾多个目标,但是在优先考虑主要目标的基础上,将剩余优化目标作为约束条件,在一定程度上达到了多目标优化的目的,为企业的调度决策提供了一定的理论依据。 表4 可供选择的调度方案Tab.4 Alternative scheduling programs p.u 本文针对柔性作业车间调度问题,将易产生非法解的互换交叉算子及插入变异算子进行改进,并验证了上述算子的性能。 同时,使用余弦相似度对个体进行相似度计算,避免在运算过程中丢失种群的多样性。最后,使用极大极小法对多目标调度模型进行约束,并对多目标柔性作业车间调度问题的实例进行仿真运算。 该研究为解决多目标柔性作业车间调度问题提供了新的思路。1.2 多目标柔性作业车间调度问题数学模型

2 遗传算法求解多目标柔性作业车间调度问题
2.1 编码与解码
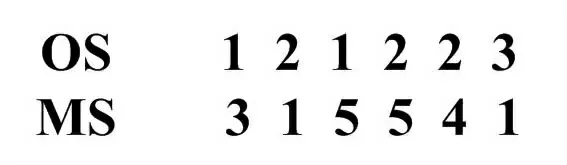
2.2 个体相似度
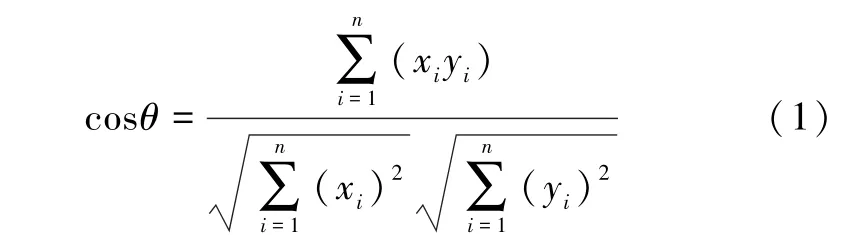
2.3 交叉操作
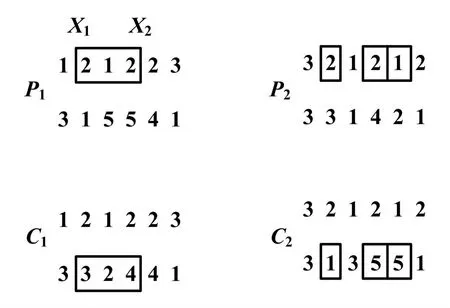
2.4 变异操作
3 试验结果与分析
3.1 交叉及变异算子有效性验证



3.2 多目标优化验证
4 结论

