大规模非结构化数据的分布式存储方法
朴承哲
(辽宁民族师范高等专科学校 民族文化与职业教育系,辽宁 沈阳 110032)
随着大数据处理技术的发展,网络中的数据量快速增加,使得数据规模持续增大,所以加大了大规模非结构化数据分布式存储难度.为了解决这一问题,需要构建优化的大规模非结构化数据分布式存储结构模型,以此提高大规模非结构化数据的优化管理能力,所以对于大规模非结构化数据分布式存储方法的研究受到人们的极大关注[1].
现阶段,对大规模非结构化数据分布式存储研究主要是建立在对数据融合和特征提取基础上,构建大规模非结构化数据分布式存储的聚类和压缩模型,通过网格分块区域聚类方法进行大规模非结构化数据分布式存储设计[2],传统的大规模非结构化数据分布式存储方法主要有以NoSQL为代表的非结构化数据分布式存储方式[3]、基于Spark的大规模非结构化数据分布式存储方法[4]、基于信息分散算法的大规模非结构化数据分布式存储方法等[5].这些方法均是通过提取大规模非结构化数据的特征量,通过关联信息融合聚类分析进行大规模非结构化数据分布式存储设计,结合压缩感知方法实现大规模非结构化数据分布式存储,但是采用传统方法进行非结构化数据分布式存储的自适应性不好,数据压缩精度不高,所用的存储开销较高,且存储耗时较长,其数据存储性能并不好.
针对上述问题,本文提出基于空间网格聚类的大规模非结构化数据分布式存储方法,并通过仿真测试进行性能验证,展示了本文方法在大规模非结构化数据分布式存储能力方面的优越性能.
1 大规模非结构化数据线性加权控制及融合
1.1 大规模非结构化数据的线性加权控制
为了实现大规模非结构化数据分布式存储优化设计,需要定义类簇之间的距离参数分布[6],以此为基础构建大规模非结构化数据多维空间分布式信息融合模型.首先采用全局分布特征融合的方法,分析大规模非结构化数据的交互特征空间分布集,通过模糊度参数特征重组的方法[7],得到第t次迭代后大规模非结构化数据多维空间分布式信息融合模型为
(1)
其中,A(t)为大规模非结构化数据的分布包络数值量,θ(t)为大规模非结构化数据调制分量.计算第k+1次迭代后大规模非结构化数据的模糊关联信息分量,并根据的密度样本分布信息[8],得到网络输入元素的自相关矩阵R为
(2)
设定Q(k)表示第k个大规模非结构化数据聚类中心的量化参数集,ε表示聚类中心与数据集分布的线性阀值,则存在以下关系式,
Q(k+1)≥ε-Q(k),
(3)
其中,Q(k+1)表示第k+1个大规模非结构化数据聚类中心的量化参数集[9].
采用模糊中心权重的方法得构建非结构化数据的交互访问控制模型,该模型具体如图1所示.
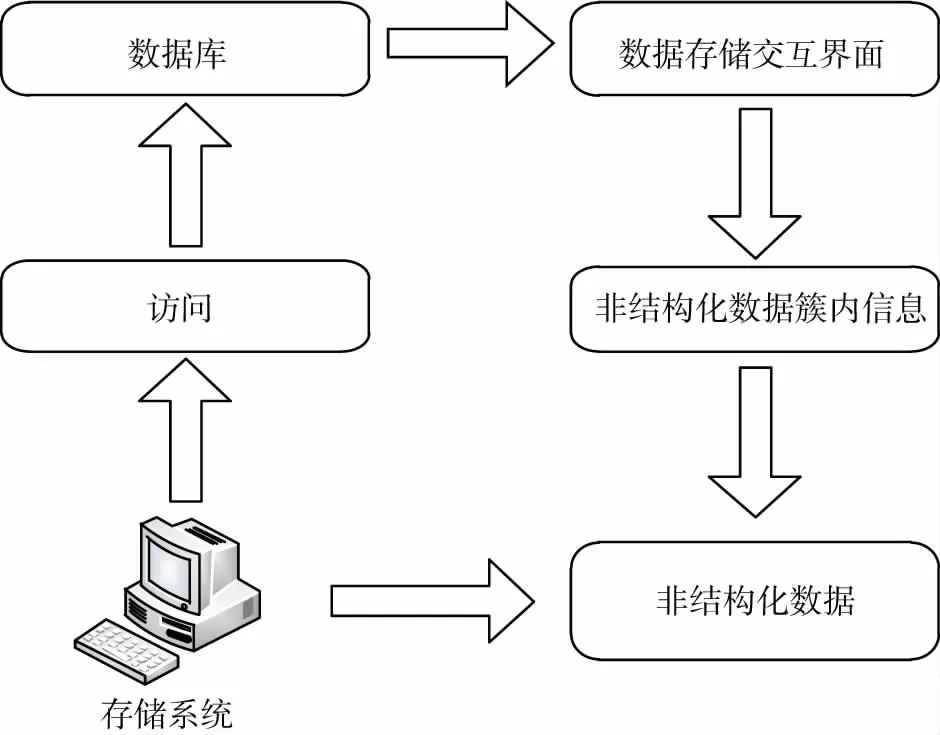
图1 大规模非结构化数据的交互访问控制模型
根据上述交互访问控制模型,进行非结构化数据簇内线性加权控制处理.在此过程中,需要先对加权系数进行计算,则其最小值可以通过公式(4)计算得出.
(4)
1.2 数据融合
根据大规模非结构化数据的特征空间分布集,采用密度最大的点作为进行大规模非结构化数据管理和自适应检测,大规模非结构化数据融合的检测统计量为
(5)
对大规模非结构化数据存储特征分量进行线性融合处理,寻找初始聚类中心.通过线性融合和二元规划设计的方法,进行大规模非结构化数据重建[10],并在初始聚类中心构建大规模非结构化数据的信息融合模型
(6)
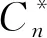
2 大规模非结构化数据分布式存储
2.1 数据特征提取
根据数据融合处理结果进行大规模非结构化数据分布式存储方法的设计.通过样本扩展和密度融合的方法进行大规模非结构化数据特征提取[11-13],采用选择随机性特征分析方法,对易混淆的大规模非结构化数据进行去重处理,以此获取大规模非结构化数据关联维特分布特征量及相似度的关系为
(7)
其中,D(A)表示大规模非结构化数据存储的额外能量开销.对大规模非结构化数据进行连续特征分解处理,假设
(8)
其中,pi为大规模非结构化数据的所有样本元素的权重,通过上述结果得到大规模非结构化数据融合的复合迁移特征量为:
(9)
当大规模非结构化数据的密度聚敛性参数满足[δ1,δ2,…,δN],通过状态结构重组,得到大规模非结构化数据的密度特征分布集
(10)
其中,|Rg|表示大规模非结构化数据的密度参数融合量.结合状态寻优控制和多模空间压缩的方法[14],得到大规模非结构化数据的聚类中心寻优控制模型为
(11)
其中,si表示大规模非结构化数据的概念集,qj表示模糊空间特征匹配集.根据聚类中心的样本元素的权重分布获取权重学习参数
(12)
其中,WjT(n)表示大规模非结构化数据存储空间主元j的统计结果;Yj(n)表示大规模非结构化数据模糊状态线性空间输出值.
根据上述分析,构建大规模非结构化数据特征提取模型为
(13)
其中,ajT(n)表示大规模非结构化数据结构重组的线性加权值,Yj-1(n)表示大规模非结构化数据存储分布的反馈输入.
综上所述,实现了大规模非结构化数据特征提取,下一步需要结合自相关融合聚类分析,进行大规模非结构化数据存储结构的优化设计,以此实现数据分布式存储.
2.2 数据分布式存储实现
根据特征提取结果进行大规模非结构化数据融合和特征空间划分,采用自相关融合聚类分析方法[15],得到大规模非结构化数据样本空间分布为
(14)
根据样本空间分布对大规模非结构化数据的个体结构信息重组,得到数据的优化存储的模糊空间分布为
(15)
根据数据预处理结果以及模糊空间分布,求大规模非结构化数据存储空间的占用期望值为
(16)
假设wj(n)为学习权重,得到存储空间中大规模非结构化数据的簇内紧密度为
(17)
其中,θjk(n)为类间相异性参数.结合簇内紧密度计算结果,对大规模非结构化数据的存储空间容量进行估计,结果为:
(18)
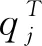
(19)
3 仿真实验与结果分析
为了验证本文方法在实现大规模非结构化数据存储优化中的应用性能,进行实验测试分析,具体的实验环境如下:操作系统为Windows7,CPU为Intel Core i5-7300HQ,内存为32 G,硬盘为500 GB,运行内存为8 G,主频为2.1 GHz,仿真软件为Matlab R2014a.
利用网络爬虫技术抓取网络中的大规模非结构化数据,并对采集到的数据进行归一化处理,将处理好的数据作为实验样本数据.其中,样本数据采集频率120 Hz,数据融合聚类的运行迭代次数为50次,数据属性间的区分度为0.46.
根据上述实验设定,构建非结构化数据分布式存储,比较应用前后的非结构化数据分布式存储的有效计算比如图2所示.
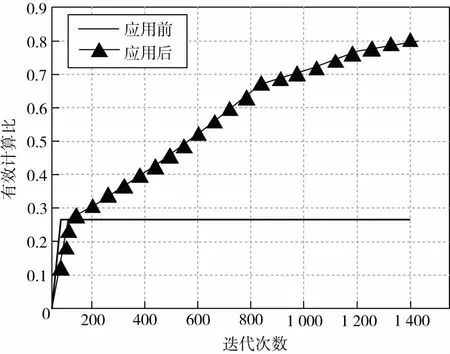
图2 有效计算比
分析图2得知,与应用前相比,大规模非结构化数据分布式存储方法应用后,数据分布式存储过程中的有效计算比较高,说明利用该方法在进行大规模非结构化数据分布式存储方面具有较高的存储能力.
为了进一步验证本文方法的应用性能,将以NoSQL为代表的存储方法(文献[3]方法)、基于Spark的存储方法(文献[4]方法)、基于信息分散算法的存储方法(文献[5]方法)作为对比方法,通过比较不同的实验指标来验证不同方法的综合性能.
测试不同方法的执行时间,得到对比结果如图3所示.
分析图3得知,文献[3]方法的执行时间在88 ms~110 ms之间,文献[4]方法的执行时间在70 ms~92 ms之间,文献[5]方法的执行时间在57 ms~77 ms之间,而本文方法的执行时间在40 ms~52 ms之间,说明采用这种方法进行大规模非结构化数据分布式存储的执行时间较短,提高了数据存储的实时性.
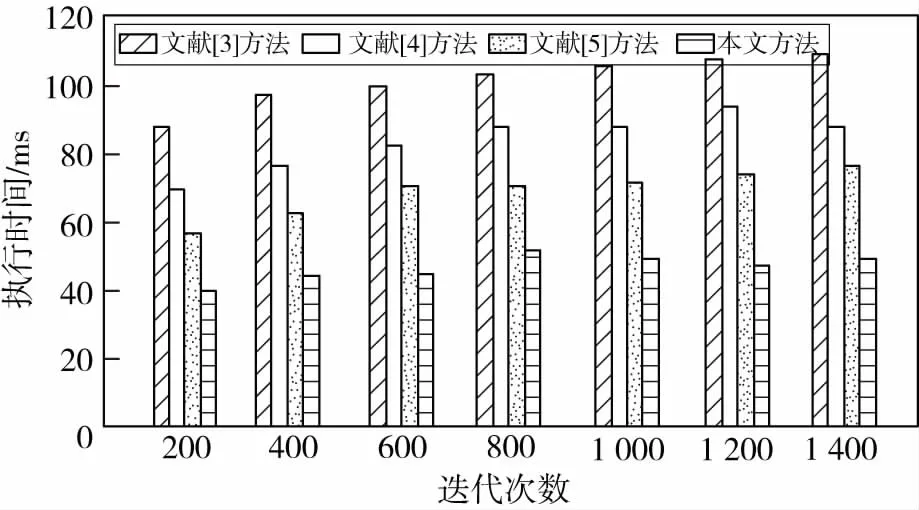
图3 执行时间测试
在此基础上,测试不同方法的数据存储的融合聚类准确性,得到对比结果如图4所示.
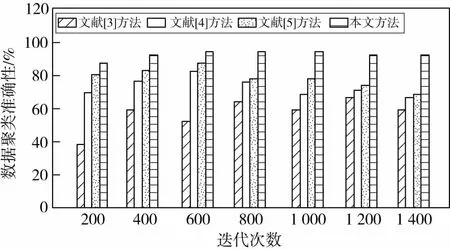
图4 数据聚类准确性测试
分析图4得知,文献[3]方法的数据聚类准确性在39%~68%之间,文献[4]方法的数据聚类准确性在66%~82%之间,文献[5]方法的数据聚类准确性在68%~85%之间,而本文方法的数据聚类准确性在87%~94%之间,说明采用这种方法进行大规模非结构化数据分布式存储,具有较高的数据聚类准确率,且明显高于其他传统方法.
4 结语
本文提出基于空间网格聚类的大规模非结构化数据分布式存储方法.构建大规模非结构化数据多维空间分布式融合模型,采用模糊中心权重聚类的方法进行大规模非结构化数据簇内特征线性加权控制处理,采用压缩感知控制方法,得到数据存储的交互结构模型,通过线性融合和二元规划设计的方法,进行大规模非结构化数据重建,根据数据预处理结果,求大规模非结构化数据存储空间的占用期望值,得到类间相异性参数,计算大规模非结构化数据的簇内分布状态特征量,实现数据存储优化设计.研究得知,本文方法进行大规模非结构化数据分布式存储的计算开销较小,降低了存储空间,提高了数据聚类准确性.

