随机邻近提升机
李金香,王福胜
(太原师范学院 数学系,山西 晋中 030619)
0 引言
随着机器学习技术的发展,从海量高维数据中建立精确预测模型的迫切需求使得人们对提升算法越来越感兴趣.提升算法的思想是通过改变训练数据的概率分布(权重分布)来学习多个弱学习器,并将它们线性组合成强学习器.提升算法起源于Freund和Schapire的组合分类器工作[1-3].进一步,Breiman和Friedman等人在论文和技术报告中阐述了提升和优化之间的突破性联系[4,5].Friedman于2001年受数值优化文献的启发提出了梯度提升算法(GBM)并讨论了弱学习器是决策树的情况[6,7].GBM在处理异构数据集(分类数据、数据缺失、高度相关数据等)方面具有优势,并有多个开源实现,例如scikitlearn[8],XGBoost[9],LightGBM[10],TF提升树[11]等.
尽管GBM在实践中表现出了优异的性能,但目前人们对这种算法的理论理解却相当有限.1999年,Mason和Collins等人首先建立了梯度提升算法的收敛性保证,但没有给出收敛速度[12,13].Bickel[14]于2006年证明了当损失函数光滑强凸时,GBM具有O(exp(1/ε2))次迭代复杂度.之后Telgarsky[15]在2012年根据GBM的原始对偶关系证明了该算法实际上只需要O(ln(1/ε))次迭代.最近,Lu和Mazumder[16]给出了更好的结果,即当损失函数是光滑且凸的,只要O(1/ε)迭代就足够了.
近年来,有关学者进一步改进了梯度提升算法.例如,Wang等人[17]在他们提出的FWboost算法中用Frank-Wolfe算法代替梯度下降,Chen和Guestrin[9]通过计算Hessian矩阵执行牛顿步而不是梯度步,Biau等人[18]结合梯度提升和Nesterov加速下降设计了AGBM.在AGBM的基础上,Lu等人[19]进一步使用修正伪残差建立了AGBM的一个变体,它的收敛速度为O(1/t2),Fouillen等人[20]基于邻近点算法提出了PBM,且结合Nesterov加速下降设计了APBM.
众所周知,梯度提升算法中时间成本最高的步骤是寻找最佳的弱学习器.例如,当弱学习器是深度为d的决策树时,训练样本数为n,特征数为p,要找到最佳的弱学习器则需要遍历n2d-1p2d-1次可能的树拆分,这说明对于中等规模的问题,即使d=1时也是难以解决的.因此,文献[16]通过使用随机化方案提出了RGBM算法,能够减少弱学习器空间中的搜索进而降低计算成本.然而RGBM只适用于损失函数可微的情况下.例如,当损失函数l(x,y)=|x-y|时,由于绝对值函数不可微则无法训练数据.因此,RGBM算法具有局限性.本文用邻近算子代替负梯度来计算伪残差,提出了新算法随机邻近提升机(RPBM),该算法不仅可以捕获数据用以准确预测,而且对可微损失函数和不可微损失函数均适用.本文还将新算法用于机器学习常用数据分类上且通过数值实验说明了RPBM的有效性.
1 算法
在本节中,我们首先给出了问题的描述和背景并回顾了RGBM算法,之后用邻近算子计算伪残差,构造了我们提出的新算法RPBM.
1.1 问题描述和背景
在本文中,假设我们给定一个参数为τ∈的基学习器类={bτ(x)∈},这些基学习器的线性组合的集合为span其中为非负整数的集合,bτt∈为其中一个基学习器且βt为其对应的加性系数.
我们的目标是获得一个对函数f的良好估计,使经验损失近似最小化:
(1)
其中l(yi,f(xi))是损失函数的数据保真度的度量.
1.2 RGBM
为了构造新算法,首先回顾一下RGBM算法[16](如算法1所示),该算法通过随机化方案减少弱学习器空间的搜索.

算法1 RGBM 输入:f0(x)=0,步长η.For t=0,…,T-1 do a)计算伪残差rit=-∂l(yi,ft(xi))∂ft(xi),i=1,…,n,rt=(r1t,r2t,…,rnt). b)通过规则1)-4)选择弱学习器的随机子集. c)在中寻找最佳弱学习器τt=argminτ∈∑ni=1(rit-bτ(xi))2. d)更新模型ft+1(x)=ft(x)+ηbτt(x).End for输出:fT(x).
2)(随机选择)我们从所有可能的弱学习器中不替换地随机选择t个弱学习器,集合用表示.
3)(随机单组选择)给定弱学习器的不重叠划分,我们随机地选择一个组,并用表示该组中弱学习器的集合.
4)(随机多组选择)给定弱学习器的不重叠划分,我们随机选择t组,并令这t组中的弱学习器的集合为.
RGBM从一个空模型f0(x)开始,在每次迭代t中计算伪残差rt∈n.由于提升的关键是学习器为弱学习器且预测空间不密集,因此,APBM在最小二乘意义上通过拟合伪残差rt寻找最佳弱学习者:最后f序列由一个最逼近rt的弱学习器更新.
RGBM使用随机化方案降低了搜索最佳弱学习器的时间成本.然而,该算法只适用于可微损失函数,对于不可微损失函数无法计算伪残差.
1.3 RPBM
在本小节中,我们提出可以同时适用于可微损失函数与不可微损失函数的新算法RPBM.RPBM与RGBM的主要区别是伪残差的不同,伪残差由邻近算子给出,其定义如下:
(2)

算法2 RPBM 输入:f0(x)=0,步长η,邻近步λ.Fort=0,…,T-1 do a)计算伪残差rit=1λproxλL(ft(xi))-ft(xi) ,i=1,…,n,rt=(r1t,r2t,…,rnt). b)通过规则1)-4)选择弱学习器的随机子集T. c)在T中寻找最佳弱学习器τt=argminτ∈∑ni=1(rit-bτ(xi))2. d)更新模型ft+1(x)=ft(x)+ηbτt(x).End for输出:fT(x).
2 数值实验
本节通过数值实验验证了所提出的RPBM(算法2)的有效性.所有的测试均在Python计算环境下的具有4GB内存的IntelCorei5处理器上进行.我们在数值实验中使用的数据集是从LIBSVM库[21]中收集到的.表1显示了这些数据集的详细信息.

表1 数据信息
对于每个数据集,我们随机选择80%作为训练数据集,其余部分作为测试数据集.提升算法在实践中常用的弱学习器有小波函数,支持向量机,树桩(即深度为1的决策树)和分类和回归树(CART)等[22].本节实验中所有的算法都使用树桩作为弱学习器,我们考虑可微的logistic损失函数l(x,y)=log2(1+e-xy)和不可微的hinge损失函数l(x,y)=max(0,1-xy).实验中我们选择2.2节介绍的规则4),其中每一组代表在单个特征上分裂的所有树桩.
实验包括两个部分.首先第一个实验说明我们提出的RPBM算法能够同时适用于可微损失函数与不可微损失函数,结果如图1所示.不同的线对应于不同的t值,即每次迭代中随机集J出现多少组.因为a9a数据集的特征为123,故蓝线t=123对应于无随机的邻近提升机PBM[20].此外,我们设置步长η=0.3.图1的左列和右列分别显示了可微logistic损失函数与不可微hinge损失函数的训练损失/测试损失与运行时间的关系.从图1中可以观察到,当t的组数变小时,每次迭代的成本显著降低,也就是说,与较大的t值相比,一个小的t值(不一定是最小的)需要更少的计算就可以实现类似甚至更小的训练/测试损失.这意味着本文所提出的RPBM对两种损失函数都具有良好的性能.
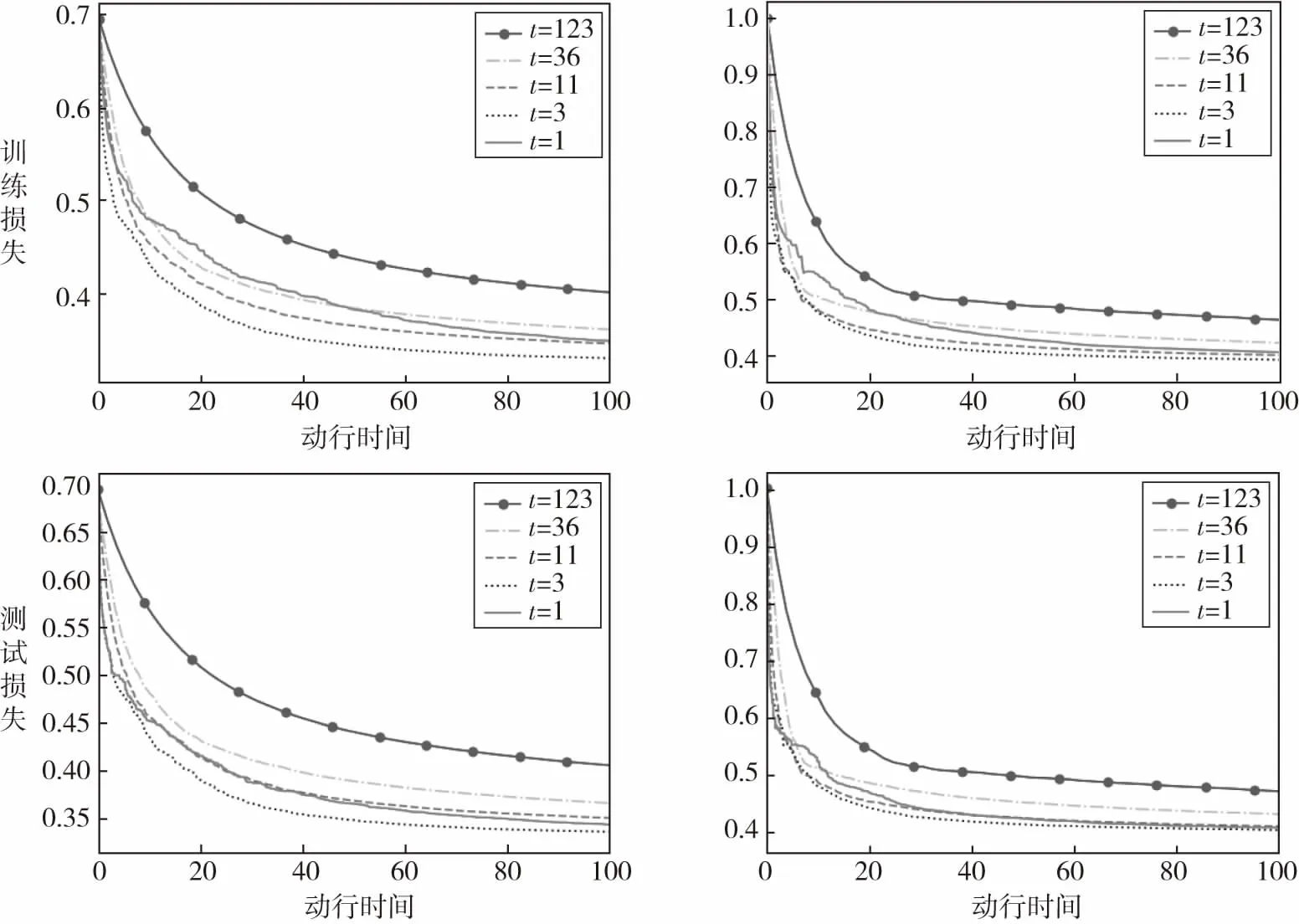
图1 Logistic损失函数(左列)与hinge损失函数(右列)的RPBM训练损失/测试损失与运行时间的关系
第二个实验展示了RPBM在不可微的hinge损失函数的泛化性能.实验中选取机器学习中五个常用分类数据集,分别是w7a,cifar10,mnist,splice,german,每个数据集的t取最大均代表无随机状态的邻近提升机(PBM).此外,算法中的步长η=0.1,邻近步λ=1,运行时间以秒为单位,具体数值实验结果见表2.
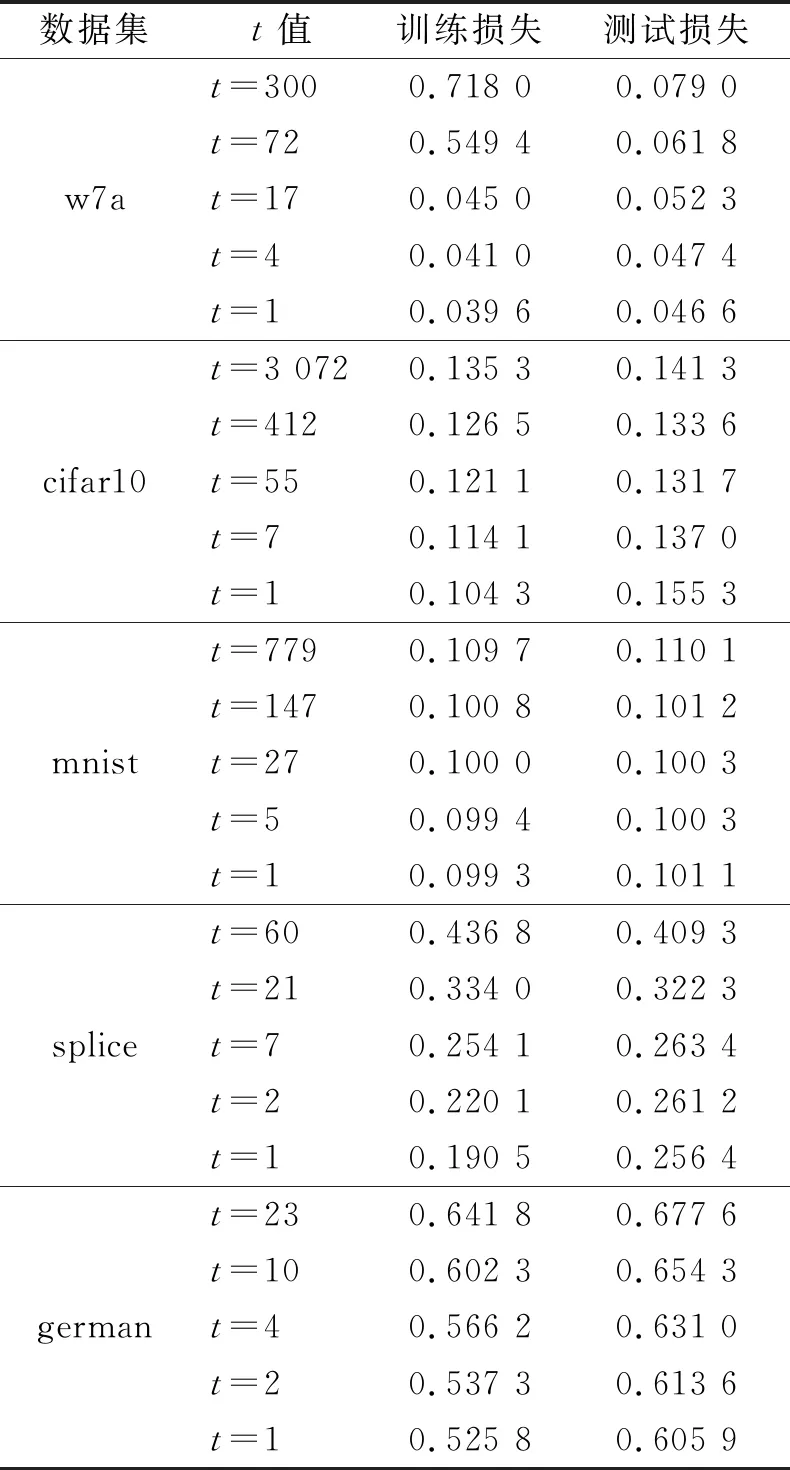
表2 RPBM在不同t值(最大的t值对应于PBM)的性能
通过表2可以看出通过使用较小的t值,RPBM可以显著地节省计算量,且训练损失与测试损失都较小.因此,随机邻近提升算法不仅可以在可微损失函数上训练数据,还可应用在不可微损失函数上,且在不同的数据集上均具有良好的性能,这说明本文提出的RPBM有效,且与已有算法比较具有优势.
3 小结
本文基于邻近点算法,用邻近算子计算伪残差,提出一种新算法RPBM,新算法克服了RGBM的局限性,可以同时应用于可微损失函数与不可微损失函数.数值实验表明,与已有的无随机的PBM相比,本文提出的RPBM可以显著降低计算成本,提高了运算效率,因而具有优良的数值表现.

