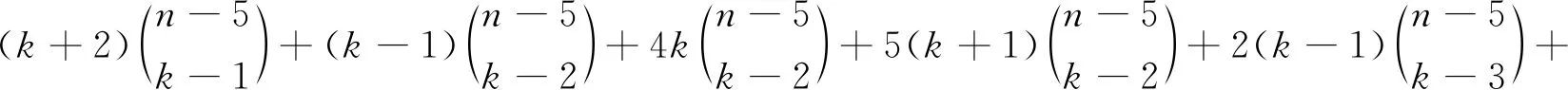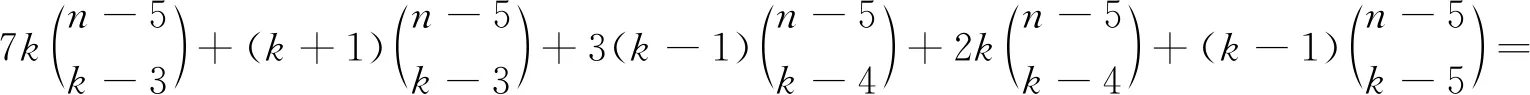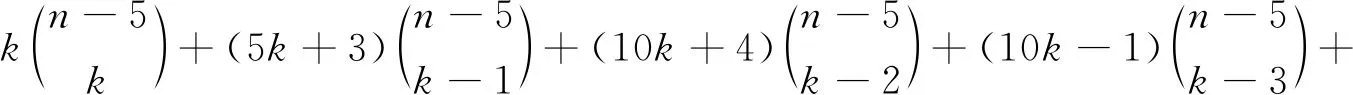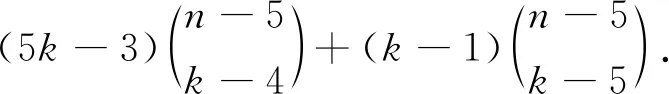两类图的k-Steiner Wiener指数的研究

郑学谦

(山西工程科技职业大学，山西 晋中 030619)

0 引言

点集S的Steiner距离d(S)间题是组合优化中经典的问题,在现代生产、生活中有着十分广泛的应用.1947年H.Wiener提出连通图G的Wiener指数[1]，1993年M.Randics 提出了超Wiener指数WW(G)的概念[2]，2016年李学良，毛亚平和Gutman提出了k-Steiner Wiener指数SWk(G)[3]，同时给出了树、完全图Kn、完全二部图Ka,b的SWk(T)指数的计算公式．2016年刘中柱，程晓胜给出了给定点着色数和匹配数的图类中的k-Steiner Wiener指数的下界并刻画了极图[4].2017年刘中柱，何莉给出了给定匹配数的树中的k-Steiner Wiener指数SWk(G)的极小值，并刻画了极图[5]．2018年Niko Tratnik给出了网图的k-Steiner Wiener指数和超k-Steiner Wiener指数[6].在此基础上，本文利用组合不等式给出了星勺图Stn-1P1C4和R(4，1×n)型图的k-Steiner Wiener指数的计算公式.

1 相关概念

定义1[7]由圈C4的点u1与n条p2路粘接所得到的图形，称为R(4，1×n)型图(图1)．

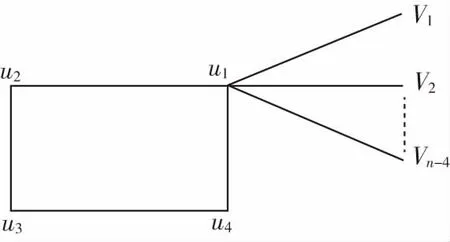
图1 R(4，1×n)型图

定义2[8]把n个顶点的星图与圈C4由一条长为1的路连接，其中路的一端点与星图的中心粘结，另一端点与圈的一个顶点粘结，所构成的图称为星勺图，记为Stn-1P1C4(图2)．

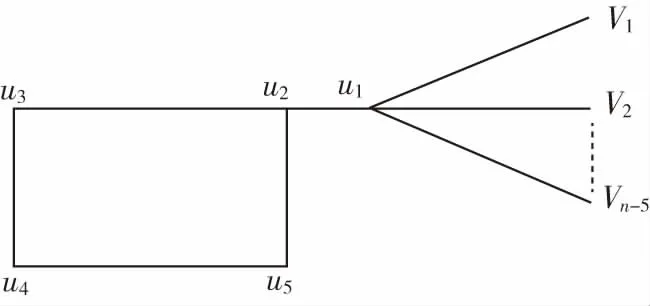
图2 星勺图Stn-1P1C4

定义3[3]点集S的Steiner距离d(S)是指包含子集S的最小子树的边数即d(S)=min{|E(T)|:S⊂V(T),T是G的子树}．k-Steiner Wiener指数SWk(G)，

2 主要结论

定理1对于R(4，1×n)型图，

证明 对于R(4，1×n)型图，U={u1,u2,u3,u4}，W={v1,…,vn-4}

当k=3,4时，S∩U=∅,或者S∩W=∅,或者S∩U≠∅且S∩W≠∅．假设S∩U=∅,S⊂W．则d(S)=k.假设S∩W=∅,S⊂U．则当k=3时，d(S)=2;当k=4时，d(S)=3.

假设S∩U≠∅且S∩W≠∅．不失一般性S={u1,u2,…,ut,v1,…,vk-t},t=1,…,4,当k=3时，d(S)=2，3,4;当k=4时，d(S)=3,4,5.

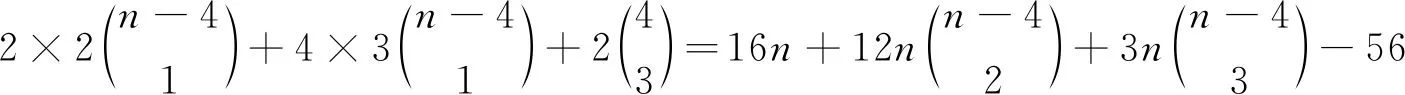
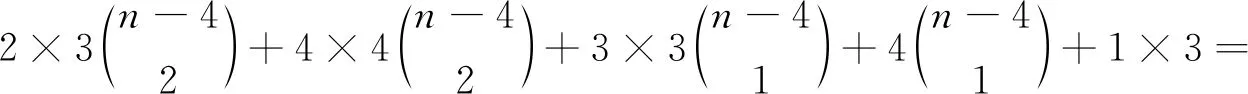
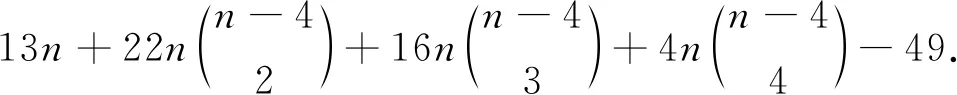
当k>4时，S∩U=∅且S∩W≠∅或者S∩U≠∅且S∩W≠∅：假设S∩U=∅且S∩W≠∅,S⊂W．则，d(S)=k.假设S∩U≠∅且S∩W≠∅．

不失一般性S={u1,u2,…,ut,v1,…,vk-t},t=1,…,4,容易得到d(S)分别k-1,k,k+1.

证明

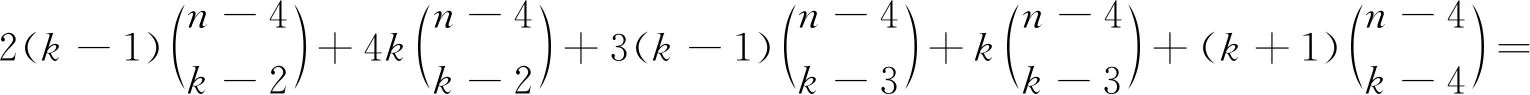
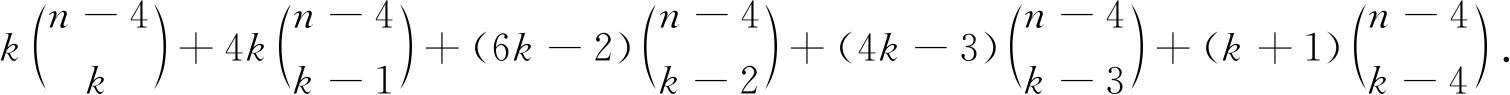
定理2对于星勺图Stn-1P1C4，

SWk(Stn-1P1C4)=

证明 对于星勺图Stn-1P1C4，U={u0,u1,u2,u3,u4}，W={v1,…,vn-5}对于任意S⊂V(G),|S|=k．

当k<5时，S∩U=∅,或者S∩W=∅,或者S∩U≠∅且S∩W≠∅．假设S∩U=∅,S⊂W．则d(S)=k.假设S∩W=∅,S⊂U．则当k=3时，d(S)=3，2;当k=4时，d(S)=4，3;当k=5时，d(S)=4.

假设S∩U≠∅且S∩W≠∅．不失一般性S={u1,u2,…,ut,v1,…,vk-t},t=0,1,…,4,当k=3时，d(S)=2，3,4,5;当k=4时，d(S)=3,4,5;当k=5时，d(S)=4,5,6,7.

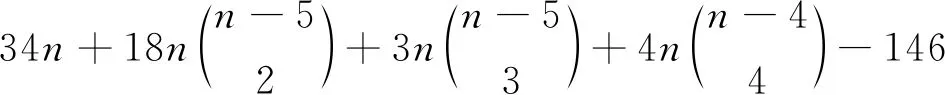
SW4(Stn-1P1C4)=

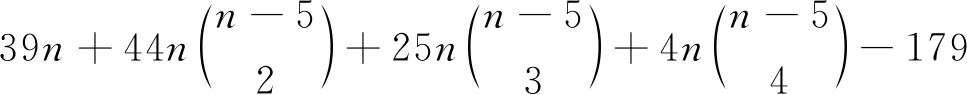
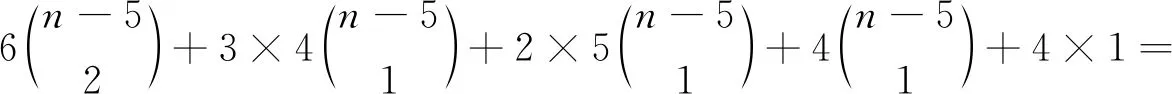
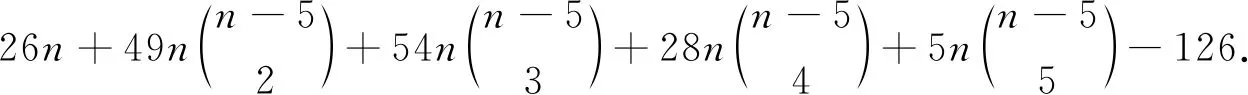
当k>5时，S∩U=∅且S∩W≠∅或者S∩U≠∅且S∩W≠∅：假设S∩U=∅且S∩W≠∅,S⊂W．则，d(S)=k.假设S∩U≠∅且S∩W≠∅．

不失一般性，S={u1,u2,…,ut,v1,…,vk-t},t=0,1,…,4,容易得到d(S)分别k-1,k,k+1,k+2,则

SWk(Stn-1P1C4)=