连续时间级联∑-Δ调制器的系统综合设计

史宜巧，赵 辉

(1.江苏电子信息职业学院 智能制造学院，江苏 淮安 223003;2.河北工程大学 信息与电气工程学院，河北 邯郸 056038)

0 引言

日益缩小的CMOS形体尺寸引发了集成电路设计的革命。由于关键设计能力仍严重滞后，使得设计成本快速增长；对于模拟和/或混合信号设计，由于诸多原因，设计开发更加困难，最重要的是缺乏商业计算机辅助设计工具和方法来有效支持设计。

高速无线和有线通信终端一般要求宽带模/数变换器(Analog-to-Digital Converters,ADCs)能够将20 MHz宽带信号数字化，且具有超过12位的有效分辨率和功耗最低，其中∑-Δ调制器是实现这些性能指标的关键；目前大多数∑-Δ调制器都采用离散(Discrete-Time,DT)电路实现，而宽带数据通信系统推动了连续时间(Continuous-Time,CT)∑-Δ调制器的使用。CT ∑-Δ调制器除了显示出固有的抗混叠滤波优势之外，还可以提供比相应的DT ∑-Δ调制器更快的运算速度和更低的功耗，而且对于一些电路误差(如时钟抖动、过回路延迟和工艺参数变化)来说，CT ∑-Δ调制器比DT ∑-Δ调制器更灵敏；其中工艺参数变化对于级联结构的实现尤为重要，这也是现有大多数硅原型中采用单回路拓扑的原因[1]。尽管单回路CT拓扑比级联CT拓扑对工艺过程的变化可能有更低的灵敏度要求，但级联CT拓扑的高稳定性使得它们对高分辨率和高信号带宽特别有吸引力[2],需要针对CT级联∑-Δ调制器这类电路的设计方法进行研究。

目前，大多数系统设计方法和工具都针对DT ∑-Δ调制器[3-5]。一方面是由于它们的广泛采用;另一方面是因为它们更容易实现。

针对CT ∑-Δ 调制器的设计方法和工具开发也得到了研究[6-11]。文献[6]基于数学方法和内部块的行为建模，提出了一种具有噪声整形的CT ∑-Δ调制器设计，在系统级和行为电路级上实现了一种补偿超循环延迟的4-阶单回路CT ∑-Δ调制器，具有78 dB的信噪比(Signal to Noise Ratio,SNR)；文献[7]提出了一种混合式CT Sigma-Delta调制器，并分析了系统中的运放有限增益带宽积、积分常数变化、环路延时和比较器失调等非理想因素；文献[8]提出了一种新的方法来分析时钟抖动对连续时间Σ-Δ调制器性能的影响，实际实例应用表明了预测与数值仿真之间的良好匹配；文献[9]为了降低连续时间Σ-Δ调制器的带内噪声，基于跳频技术建立了一种抗混叠模型，然后利用该模型导出了给定的非重叠持续时间的带内噪声和抗混叠的解析表达式，通过仿真验证了所得结果；文献[10]设计了一个真分式噪声传递函数使调制器所允许的最大环路延时提升至2个时钟周期，采用高能效的逐次逼近型ADC作为内部量化器，并采用Matlab综合出真分式噪声传递函数，基于Simulink仿真平台建模了反馈-前馈混合结构的三阶调制器结构；文献[11]基于Matlab/Simulink平台提出了一种∑-Δ变换器设计方法来找到合适的拓扑结构和块级规范，并采用这种方法实现了一个16位、250 kHz信号带宽的开关电容∑-Δ变换器；文献[12]提出了一种SATA Ⅲ的6 GHz Sigma-Delta小数分频扩频时钟产生器的设计，克服了整数分频器扩频时钟产生器的缺点,较好地满足了SATA Ⅲ的要求；文献[13]针对Sigma-Delta ADC实现高精度和降低系统功耗问题，对二阶Sigma-Delta调制器的非理想因素进行数学建模分析，并利用SDtoolbox进行了仿真验证，对调制器进行了电路级设计。结果表明，调制器输出信号的带内信噪比为83.5 dB，总功耗为1.8 mW。

本文针对CT级联∑-Δ调制器提出的完整系统综合设计方法，其创新点在于通过设计空间探索和传输规范构建起成本函数来获得满足调制器性能指标的可选体系结构的集合，从而得到满足调制器性能指标的不同构建模块的非理想性的最大值，并通过实验结果验证了所提出设计方法的有效性。

1 系统综合设计原理概述

本文提出的系统综合设计过程原理如图1所示，设计流程主要包括3个阶段：结构综合、高级尺寸调整和电路级尺寸调整。

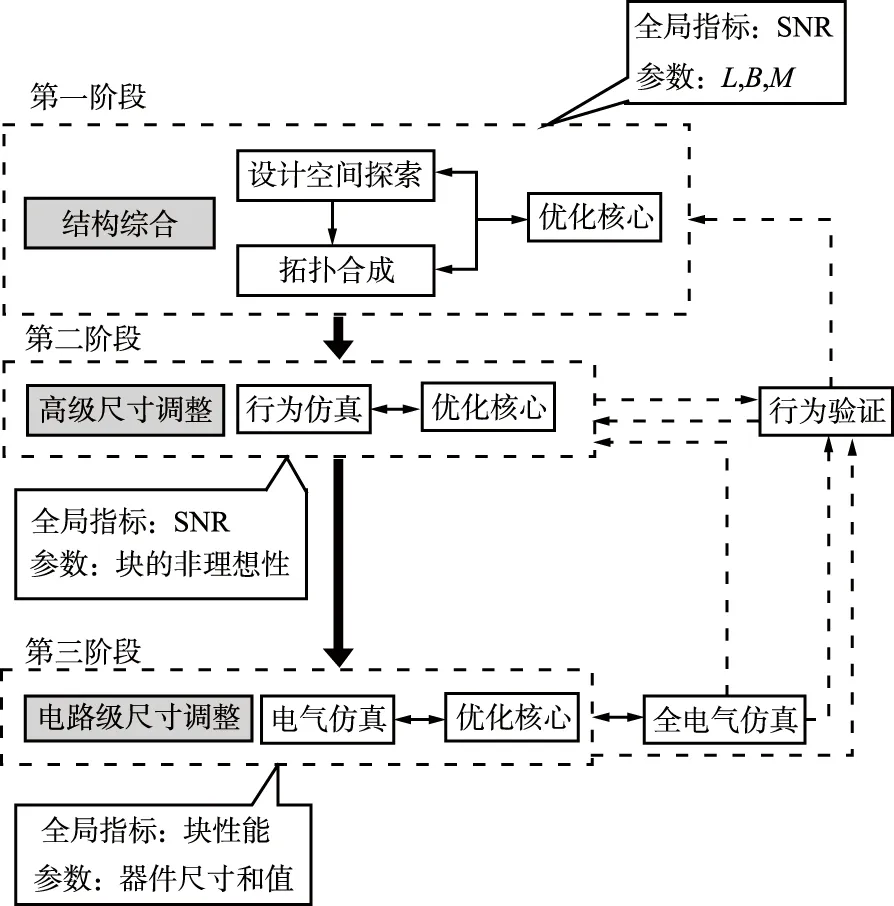
图1 综合设计过程原理Fig.1 Principles of synthetical design process

在结构综合设计阶段，设计空间探索和传输规范依赖于某种性能评估(例如在某种抽象层次上采用建模方程和行为仿真)与优化器的交互。这个过程的重要部分是合适的成本函数构建，它是对设计与目标性能的一致性程度的量化，也是求解成本函数的一种快速而准确的方法，以及在设计空间上生成后续推动力的有效技术。

其中的优化核心有2个步骤：第一步是应用全局优化技术，第二步是采用具体技术进行局部优化[11-12]。

优化问题从数学上表述为：

(1)

式中，yi(x)为第i个设计目标的值(如最小化功耗)；yj(x)为第j个设计约束的值(如信噪比大于70 dB)；Yj为这种设计规范的目标值；x为设计变量向量。设计目标、设计约束和变量依赖于实际的优化任务。例如，块非理想性(如放大器增益)是高级尺寸调整的设计变量，但却是电路级尺寸调整的设计约束。设计约束定义了有效设计的集合(也称为可行性设计空间)，而设计目标(如功耗或面积占用)是对设计的最优性进行表征，并给出有效解决方案之间的权衡；尺寸调整机制是通过采用单一成本函数进行优化的。对于设计空间中不满足设计约束的点，成本函数定义为：

Ψ(x)=max[-wjlg(yj/Yj)]，

(2)

式中，wj为与第j个设计约束相关联的权重。对于可行的设计空间点来说，成本函数定义为：

Ψ(x)=Φ(yi)=-∑iwilg(|yi|)，

(3)

式中，wi是与第i个设计目标相关联的权重。

结构综合设计阶段的输入是CT ∑-Δ调制器要求的性能指标和工艺过程信息。方法从体系结构探索开始，主要是尝试获得可选体系结构，这些体系结构由调制器的阶数L、量化器的位数B和过采样率M确定，从而获得一定的信噪比(Signal to Noise Ratio,SNR)指标；这种体系结构探索是通过解析表达式来实现的，解析表达式是对限制可实现信噪比的主要误差源进行建模，并结合优化核心。体系结构探索的输出是可能满足调制器性能指标的可选体系结构的集合。

接下来是拓扑合成，即级联结构、级内和级间环路滤波器传递函数和消除逻辑(Cancellation Logic,CL)函数的确定。本文采用CT域中的直接合成方法，而不采用更一般的等效DT拓扑的DT到CT变换。

第二个阶段的高级尺寸调整阶段的输入是合成拓扑的结构描述。随后的自动尺寸调整过程采用行为仿真器以及全局优化程序来得到在仍然满足调制器性能指标的情况下可接受的不同构建模块的非理想性的最大值。在这个层次上，功耗估计非常重要，因为要建立与每个构建模块性能指标之间的关系。然后，通过采用行为仿真器在全部工作条件(过程、温度和电源变化)下验证采用传输构建模块指标的调制器性能。如果验证表明某些性能指标下降超过了某个约束，则在更严格的约束下再次执行高级综合和/或体系结构合成。

系统综合设计过程的最后一个阶段是电路级尺寸调整，即调整各构建模块的尺寸。电路级尺寸调整阶段的输入是每个构建模块的性能要求(如放大器的DC增益和带宽，或比较器的滞后和偏移)。这种尺寸调整是通过将电气仿真器与前面的全局优化过程[11,14]相结合来实现的。

2 系统综合设计的具体实现

2.1 第一阶段的结构综合

2.1.1 高级性能建模和体系结构探索

设计空间探索和传输规范依赖于全局优化器和快速性能估计器之间的迭代交互。在高的抽象层次上，调制器的性能是由一组封闭形式的方程来建模的，这组方程包含了关于控制系统行为的设计参数的基本信息。∑-Δ调制器的SNR为：

(4)

式中，A为输入信号的幅值；Pe为带内误差功率。理想情况下，带内误差功率仅包含量化噪声功率Peq：

(5)

式中，Xfs为量化器的全尺寸(满标度)；B为量化器的位数；fs为采样频率；NTF(·)为噪声传递函数；Bw为信号带宽。但在实际中，带内误差功率包含因量化误差功率放大、数/模变换器非线性、电容失配、热噪声、时钟抖动、有限的放大器增益和不完全放大器沉降等因素而产生的项，因此，实际的带内误差功率应为：

Pe=Peq+ΔPeq+Pe-thermal+Pe-jitter+Pe-DAC+Pe-settling，

(6)

式中，Pe-thermal为热噪声功率；Pe-jitter为时钟抖动功率；Pe-DAC为数/模变换器非线性引起的功率；Pe-settling为不完全放大器沉降等因素引起的功率。

不同于其他类型的∑-Δ调制器，高速CT ∑-Δ调制器中的主要误差源是由时钟抖动引起的。因此，抖动影响的建模至关重要。采用非归零(Non-Return-to-Zero,NRZ)DAC的CT ∑-Δ调制器中由时钟抖动引起的误差功率可表示为[15-16]：

(7)

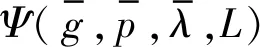
利用式(6)中的主要误差功率项(式(5)和式(7)所示)和优化核相结合，可以得到在NTF零点分布和对时钟抖动不敏感性方面有更好性能的可选结构[17]，每个可选结构由3个一组的阶数、比特数和过采样率{L，B，M}值表示。

通常，在后面的阶段要考虑若干个3个一组的{L，B，M}值，原因如下：第一，由于建模方程是近似的，因此不能确保当采用包含特定物理实现的非理想性更精确的模型时，所选取的结构将继续满足性能指标。最优结构是在满足性能约束的条件下，使得诸如功耗或面积占用等目标最小化。在体系结构层面探索的准则包括考虑诸如阶数最小化、过采样率最小化(以避免功耗方面的不可行采样频率)，以及量化器的比特数最小化(以避免采用线性化技术)。因此，在这个层面可能考虑的功率或面积占用最小化标准是定性的。因此，在整个综合过程中，可选体系结构的任何排序都可能发生大的变化。但在这个阶段，这并不是最关键的，因为所期望的结果只是一组可选拓扑，当在随后的设计步骤中考虑更详细的模型时，将对这些可选拓扑进行修剪。

2.1.2 拓扑合成

级联CT ∑-Δ调制器结构通常是在DT域中通过首先合成具有相同性能指标的∑-Δ调制器，然后将DT应用于保持相同数字消除逻辑的CT变换来合成的。然而，从这种变换和保持消除逻辑获得一个功能性CT调制器需要每个状态变量，且要求DAC输出连接到后级的积分器输入，图2给出了一个采用DT到CT变换的2-1-1结构。这意味着需要大量的模拟器件(半导体和放大器)，进而意味着更大的面积、更高的功耗和对电路容限更高的灵敏度。

图2 采用DT到CT变换的2-1-1 CT ∑-Δ调制器原理图Fig.2 Schematic diagram of 2-1-1 CT∑-Δ modulator using DT to CT transformation

为了克服上述缺点，本文提出一种直接在CT域中的合成方法。考虑图1所示有m级的级联CT ∑-Δ调制器的一般情形，从yi(s)到第j个量化器输入的传递函数表示为：

(8)

合成方法从最优地将单回路传递函数Fij(s)的极点放置在使信号带宽中NTF最小化的位置[10,16]开始，即从放置相应NTF的零点所要求的标称值开始，在动态范围和稳定性方面优化调制器的性能。为此，这些系数在其标称值的范围内变化，在保持稳定性的同时使得信噪比最大化。然后，通过级间集成路径自动确定传输函数Fij(s)。

如果调制器输入x(t)设置为零，则可以得到每级的输出yk(z)为：

(9)

式中，Z为z-变换；L-1为Laplace(拉普拉斯)逆变换。

调制器的输出yo为：

(10)

式中，CLk(z)为第k级的部分消除逻辑传递函数，计算如下：

(11)

式中，最后一级的部分消除逻辑传递函数CLm(z)可以选取为最简单的形式，以保持要求的噪声整形。通过采用这种方法合成的2-1-1 CT ∑-Δ调制器原理如图3所示。

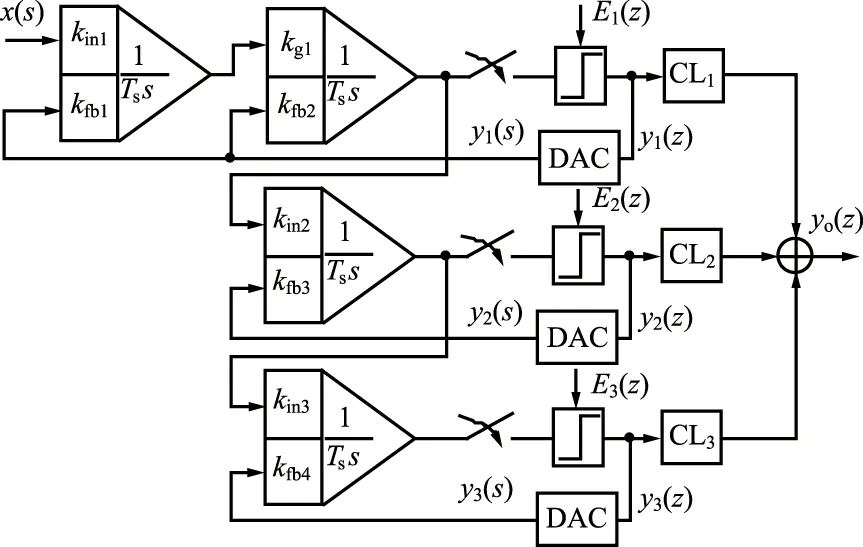
图3 采用直接合成的2-1-1 CT∑-Δ调制器原理图Fig.3 Schematic diagram of 2-1-1 CT∑-Δ modulator using direct synthesis

显然，图3的电路比图2简单，同时对参数容限有更好的灵敏度。

2.2 第二阶段的高级尺寸调整

这个阶段主要是行为建模和仿真。传输规范和验证要求性能评价机制的精度要高于式(5)～式(7)等近似方程给出的精度，此外，这种性能评价通常是在迭代优化过程中进行。因此，仿真效率对于合成过程至关重要。

由于CT ∑-Δ调制器是强非线性采样数据电路，它的主要性能指标的仿真必须在时域中进行，并因其过采样特性，需要长时间的瞬态仿真来评估它们的主要性能指标。晶体管级的仿真会导致过长的计算时间，因此本文采用行为仿真来实现仿真精度和效率之间的合适权衡。具体来说，把调制器划分为子块(如积分器和量化器等)，把这些子块用一组方程建模，建模方程包含主要的子块功能性和最重要的非理想特性。本文采用Matlab/Simulink[18]作为实现平台，通过Matlab求解器集成的一组连续时间状态空间方程来描述连续时间构建模块的行为模型。这种机制可以通过嵌入C语言程序来建模非理想特性，而无需互连许多Simulink基本模块。采用行为仿真器建模的基本构建模块以及其非理想特性如表1所示。

表1 采用行为仿真器建模的基本构建模块和非理想特性Tab.1 Basic building blocks and non-idealities modeled in the behavioral simulator

建模中的工具箱包括考虑不同电路实现的CT构建模块的几个库：gm-C、gm-MC、有源-RC和MOSFET-C。

行为仿真器与优化工具相结合可以有效地实现CT ∑-Δ调制器的高级尺寸调整，即在满足调制器性能要求下，获得可容许的构建模块的最大非理想性。

2.3 电路级尺寸调整

对于全部块的大小，在标称点和几个关键工艺角，在电气层次上对完整的调制器进行最终验证。验证采用在电气层面上提取的信息，通过行为层面上更详尽的验证(所有过程、温度和电源变化)得以补充。如果性能退化超过可接受的裕量，则将在电路和/或调制器层面上进行重新设计迭代，优化时结合每个构建模块的设计理论知识。在优化层次上，设计理论知识又涉及到可行性空间方面，从而提高综合过程的效率和优化效果。

3 系统综合设计方法的实证研究

为此，采用提出的系统综合设计方法来实现一种有线通信应用的CT 级联∑-Δ调制器，其目标技术指标是12位和20 MHz信号带宽，系统级信噪比要求大于70 dB。

根据结构探索过程的不同步骤，选取3种5-阶(L=5)级联∑-Δ调制器：2-1-1-1、2-2-1和3-2拓扑。图4(a)所示为只保留了最终合成步骤的拓扑原理图，它由一个2-2-1拓扑构成。为减少抖动的影响，在fs=240 MHz(M=6)、B=4和在全部级的NRZ DAC提供时钟。

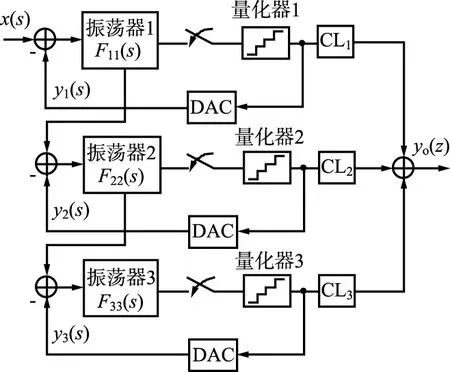
(a) 调制器原理图

级内和级间传递函数Fij(s)可写为：

(12)

式中，ωp1,2表示极点频率的最佳位置；系数bij是通过基于仿真使得动态范围最优的优化过程得到的。

从放置相应的NTF的零点所要求的标称值开始，这些系数的变化范围在其标称值的±20%附近，以便在保持稳定的同时获得最大信噪比。部分消除逻辑传递函数CLk(z)从式(11)计算得到：

CL1=z-1(n14+n13z-1+n12z-2+n11z-3+n10z-4),

CL2=z-1(n22+n21z-1+n20z-2)(1-2cos(Tsωp1)z-1+z-2),

CL3=(1-2cos(Tsωp1)z-1+z-2)(1-2cos(Tsωp2)z-1+z-2),

式中，

式中，Ts=1/fs为采样周期。

图4(b)所示为调制器的原理电路实现，表2所示为优化过程得到的结果，其中包括环路滤波器系数ki和采用的电容Ci的值。

表2 CT级联∑-Δ调制器的环路滤波器系数Tab.2 Loop filter coefficients of CT cascaded∑-Δ modulator

调制器采用高级尺寸调整，即将系统级指标(12位和20 MHz)映射到构建模块指标中，采用全局优化选择设计参数。表3所示为尺寸调整过程得到的结果，给出了满足所要求的调制器性能可容许的非理想性(构建块级)的最大(最小)值。注意，表3中只列出了对调制器性能有重要影响的那些非理想性指标。

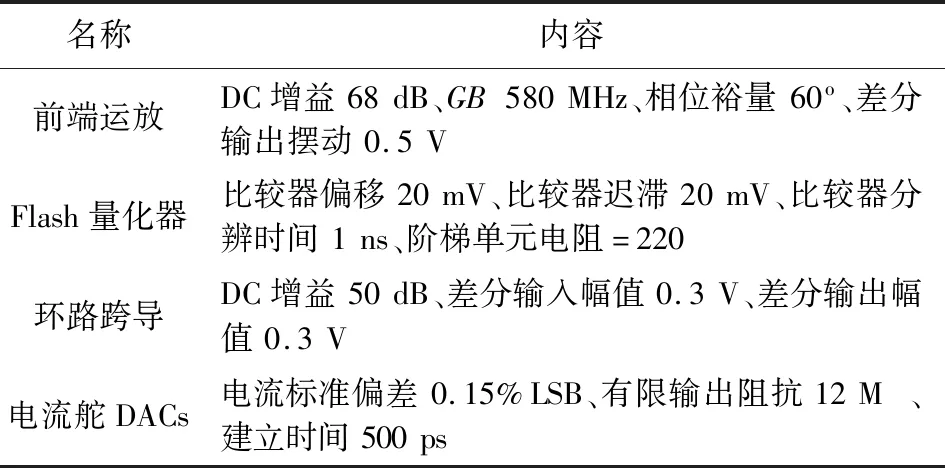
表3 调制器的高级尺寸调整Tab.3 The high-level sizing of modulator

构建模块包括前端运放、环路滤波器跨导、量化器和DACs，是通过应用单元级尺寸调整(即电路级尺寸调整)工具[11,14]来设计的。由于篇幅所限，这里只给出了前端运放尺寸调整的合成结果。前端运放及其共模反馈电路的原理图如图5所示，它是一种具有增益增强的全差分折叠共射共基放大器拓扑。经过一个仿真循环优化过程，得到尺寸调整后的电路的电性能如表4所示。类似的尺寸调整方法适用于其他构建模块。

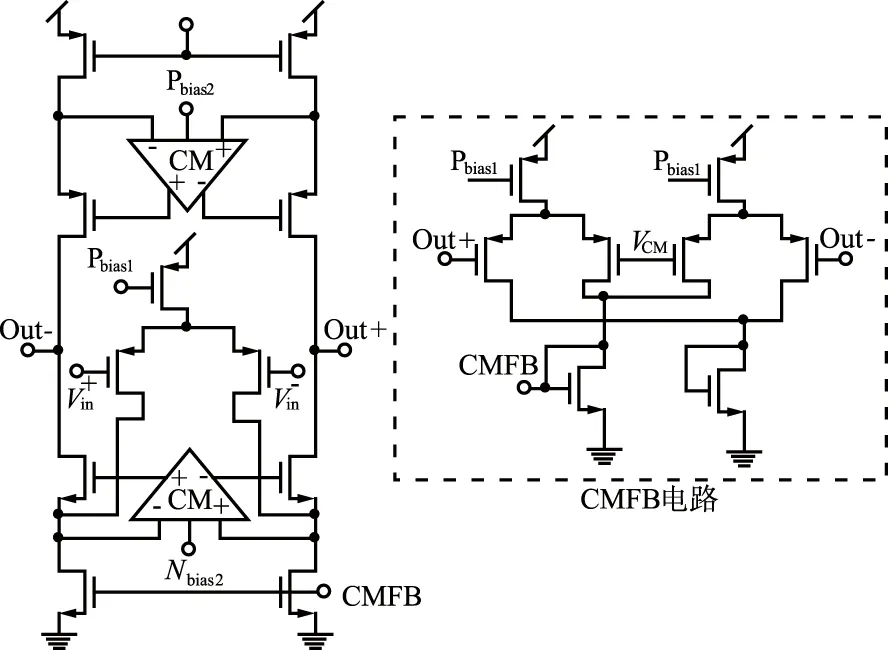
图5 前端运算放大器Fig.5 Front-end operational amplifier

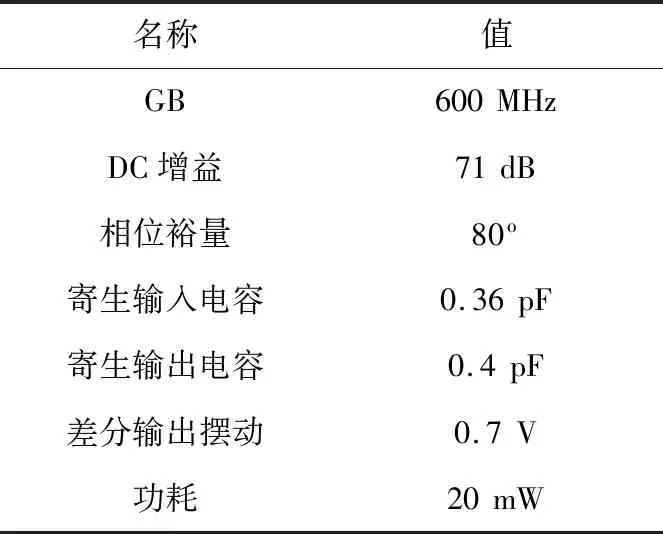
表4 前端运放的电性能Tab.4 Electrical performance of front end operational amplifiers

最后，采用130 nm CMOS工艺实现的调制器的微缩版图(带焊盘)如图6所示。

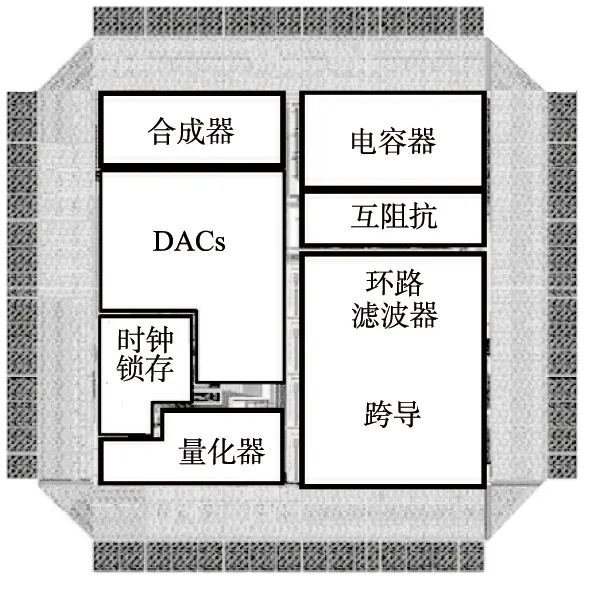
图6 调制器微缩版图(带焊盘)Fig.6 Modulator miniature layout (welding plate)

对生成后的调制器性能进行实验。测得总的占用面积仅为2.33 mm2(包括焊盘)，单电源1.2 V电压时的功耗为70 mW；图7所示为幅值为-6.5 dBV、频率为1.76 MHz的正弦波输入得到的调制器输出频谱。可以看到，在目标技术指标12位和20 MHz信号带宽内最大信噪比约为80 dB，即使在最坏的失配情况下，也可获得大于74 dB的信噪比，结果完全达到系统级设计指标要求。

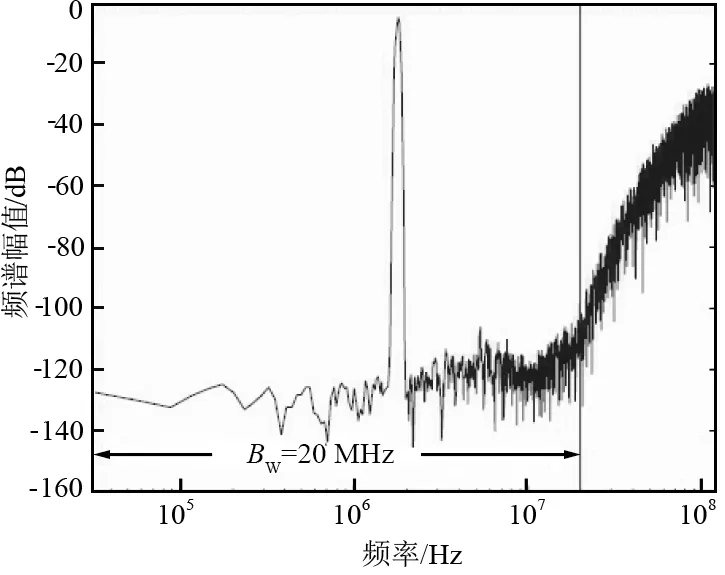
图7 调制器的输出频谱Fig.7 The output spectrum of the modulator

图8所示为采用双音输入信号(f1=1.49 MHz,f2=2.02 MHz,)测试调制器得到的结果。可见，即使存在三阶互调失真导致性能下降，但仍能获得大于76 dB的信噪比。可见，采用本文的系统综合设计方法能够实现CT ∑-Δ调制器的目标设计。

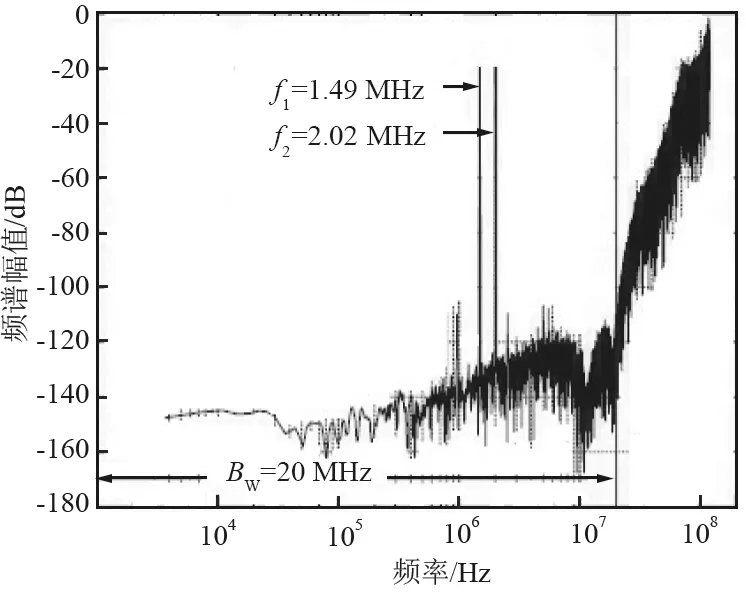
图8 双音输入信号测试的输出频谱Fig.8 The output spectrum of a two-tone input signal test

4 结束语

本文提出了一种支持CT级联 ∑-Δ调制器设计的完整系统的综合设计方法，详细讨论了从设计理论原理到设计过程的实现。这种自顶向下和自底向上的系统综合设计方法，有助于设计人员将设计理论、合成方法、行为仿真和优化工具的适当结合来完成CT级联∑-Δ调制器的设计，从而简化这类高性能调制器的设计复杂性。