对地观测卫星动态任务调度优化算法研究

陈 昊，赵 斐，白建东

(北京跟踪与通信技术研究所，北京 100094)

0 引言

对地观测卫星任务规划的目标就是选择需要观测的目标、确定观测的卫星遥感器、观测开始时间和结束时间。对于多颗卫星、多种遥感器和多个任务需求的情况下，如何充分分配卫星资源、高效地完成任务和发挥对地观测卫星系统的能力，生成一个满意的卫星任务规划方案，显得非常重要。

国内外对于卫星对地观测任务规划问题已经开展了较多研究。P.Wang等[1-2]建立了约束规划模型，并比较了贪婪算法、动态规划、约束规划和局部搜索4种不同的求解策略；Han S M等[3-4]建立多目标敏捷卫星调度模型，并提出一种偏好的随机遗传算法求解该问题，研究了多种选择策略和解码策略；LI J F等[5]利用敏捷卫星的高机动性优势，提出了一种针对区域目标的最优条带划分和观测窗口计算方法；国内以国防科学技术大学信息系统工程团队为代表，在单星以及多星对地观测的任务规划问题上进行了广泛和深入的研究，取得了一系列的研究成果[6-14]。

但是，截止目前，国内外对于卫星对地观测任务规划问题的研究主要是针对静态任务，即给定一定时间(通常为1天)进行一次，在调度前卫星观测任务是预先提交确定的，规划方案一经生成便不再改变，方案提交给卫星进行执行完成即可。然而这种情况在应急任务时并不合适。此外，卫星系统在运行过程中因为各种原因，导致当前调度方案无法顺利执行下去，也需要对调度方案进行动态调整。

本文针对卫星任务规划调度的动态调整需求，在每个动态调度决策点，将所有的任务划分为已完成任务、已安排任务和新任务。首先对卫星任务动态调度问题进行统一描述，包括新任务的插入、已安排任务的取消、任务优先级的变更、天气条件的变化和卫星资源状态的变化描述为新任务的插入；其次以最大任务收益和最小任务扰动测度为目标函数构建完成任务动态调度优化模型，设计可见时间窗口拥挤度和执行时刻点重叠度2种启发式因子，基于启发式智能ISR-HA算法寻求最优任务编排结果。

1 任务动态调度问题的统一描述

由于卫星系统在运行过程中可能会遇到各种环境变化、任务扰动，导致当前调度方案无法顺利地执行下去，需要对调度方案进行动态调整。卫星任务优化调度技术路径如图1所示。

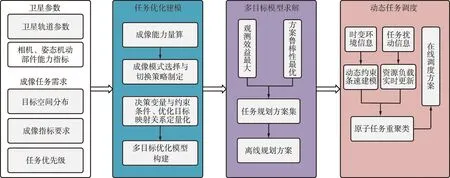
图1 卫星任务优化调度技术路径Fig.1 Technical approach to optimal sechduling of satellite mission

本文分析各类扰动对姿态机动时间的影响，结合星上实时状态信息，把动态调度问题统一用插入任务的卫星动态调度问题进行描述，在每个动态调度决策点，将所有的任务划分为3种类型：己完成任务、已安排任务和新任务，如图2所示。已完成任务不需要再考虑；已安排任务表示在当前调度方案中尚未执行的任务；新任务指的是新到达任务或因不满足约束条件而暂时没有安排进当前调度方案的任务。任务动态调整指的是有新任务或者是已安排任务中，因约束条件改变导致无法按当前调度方案执行，或当约束条件改变而导致某些任务无法按当前调度方案执行时，已安排任务就转化为新任务。

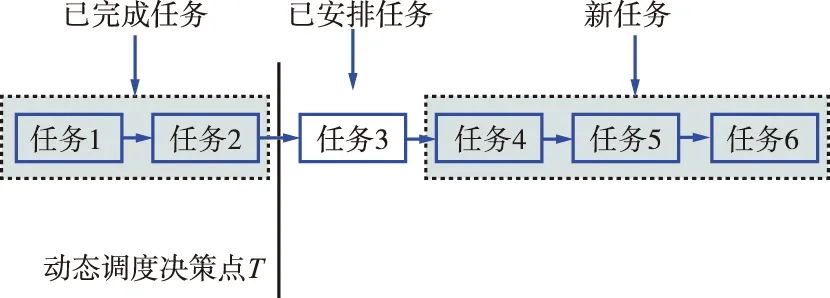
图2 动态调度任务的划分Fig.2 Partition of dynamic sechduling tasks

可以把未安排任务看作是新任务集中的任务，并将取消的任务从已安排任务集中删除；针对任务优先级变化，如已安排任务的收益变低，或未安排任务收益变高，需将新任务集中的高收益任务插入到调度方案中，同时可将低收益任务从调度方案中调整出任务集；对天气情况变化和卫星资源变化，需要把这些因天气条件不满足暂无法执行的任务从已安排任务集调整到新任务集中，必要时将后续优先级低的任务从调度方案中调整出来。因此，动态调度调整问题中虽然扰动的类型不同，但本质上都可以归结为一类插入任务的动态调度问题。

2 卫星任务动态调度优化模型

2.1 约束满足问题

在人工智能领域中有一个比较重要的问题就是约束满足问题。一个约束满足问题由3部分组成：① 变量集合；② 对应变量所属的值域；③ 求解过程中需要满足的相关约束集合。

约束满足问题的求解目标是满足各项约束条件的前提下，为在每个变量相应的值域范围内取某一个特定的值。约束满足问题的描述形式有多种，一种较为有代表性的定义是把约束满足问题以一个三元组P=〈V,D,C〉来表示，其中：V为变量集，V={V1,V2,...,Vn}；D为定义域集，D={D1,D2,...,Dn}，其中Di为Vi的值域；C为约束关系集，C={C1,C2,...,Cm}，每个约束Cj与V的一个子集相关，即Cj≤Vsub，其中Vsub是约束中包含的变量，Vsub=Vj1×Vj2×...×Vjn；R是与变量相关的值域：R=Dj1×Dj2×...×Djn，即每个约束关系确定了它所涉及的变量定义域的笛卡儿积的一个子集；R>表示一个约束关系。

约束满足问题的解是组合{〈V1,d1〉,〈V2,d2〉,...,〈Vn,dn〉}，该组合满足所有相关的约束条件，其中di∈Di。

在优化模型构建前，首先对问题进行假设，关注核心约束条件，实现模型约束条件的简化，然后提出动态调度优化的目标函数与约束条件。多星任务动态调度问题涉及多颗卫星，每颗卫星都具有固定的运行状态。同时，该问题也涉及多个地面观测目标，每个地面观测目标均有明确的经纬度信息。受卫星运行过程的限制，卫星在一天内通过地面观测目标的时间是有限的，此时间范围称为可见时间窗口。可用时间窗相对于卫星需要执行的任务而言往往是不足的，所以，需要编排合理的卫星调度执行方案。

S：表示卫星资源集合，即S={s1,s2,...,sn}；

Td：表示动态调度时刻点；

OriginTasks：表示原调度方案集合，即OriginTasks={t1,t2,...,tm}，其中ti表示原调度方案中第i个任务；

NewTasks：表示新任务集合，即NewTasks={t1,t2,...,tp}，其中ti表示新任务集中第i个任务；

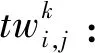
Values：表示所有任务的价值集合，Values={v1,v2,...,vm+p}，其中任务数为m+p，即新任务与原调度方案任务数之和；

disturbi：布尔变量，表示任务ti是否受到扰动，是则为1，否则为0，其中ti∈OriginTasks；

tci：表示卫星遥感器的相邻任务间切换时间，即tci表示卫星si的遥感器转换时间，由于之前假设一个卫星只携带一种传感器，那么si∈S；

di：表示任务ti需要满足的持续观测时间，其中ti∈NewTasks∪OriginTasks；

ai：表示任务ti到达的时刻点，其中ti∈NewTasks∪OriginTasks；

ei：表示任务ti必须在此之前完成，即任务的完成截止期限，其中ti∈NewTasks∪OriginTasks；

tmini：表示卫星si的遥感器最小开机时间；

tmaxi：表示卫星si的遥感器最长开机时间。

2.2任务动态调度模型

卫星动态调度问题可描述为：已知卫星资源S，在动态调度决策时刻点Td，有一批新任务集NewTasks需要插入到原调度方案中OriginTasks。在满足卫星任务各种约束条件下，获取尽量大的任务总价值，由于动态调度问题需要满足时效性，所以应保证尽量快地制定出新的调度方案，并保证新方案与原调度方案的差异性越小越好。

针对对地观测卫星在执行初始调度方案的过程中经常遇到各种突发事件的情况，分析导致动态调度的主要扰动因素以及主要的约束条件，并将其归为一类复杂约束下的新任务插入问题，以最大化完成任务优先级之和，并将对原调度计划调整最小作为另一个目标，建立了具有两级优化目标的动态约束满足问题模型。

卫星对地观测动态调度问题可以描述为七元组：

〈SimTime,S,Td,OriginTasks,Windows,Constraints,Values〉。

SimTime为整个仿真周期，SimTime=[tb,te]，tb表示仿真周期起始点，te表示仿真周期结束点。TimeWindows为所有任务的时间窗口集，即TimeWindows={tw1,tw2,...,twm+p}。Constraints表示任务所要满足的所有约束集。

优化目标函数如下：

(1)

(2)

式(1)为第一级目标，表示最大化完成任务总权值，反映了调度方案整体的收益。式(2)为第二级目标，表示最小化受干扰的原计划任务数目，反映了新任务对原调度方案的震荡程度。

约束条件如下：

(3)

(4)

(5)

(6)

(7)

式(3)表示每个任务最多被某颗卫星执行一次， 如果任务i被成功安排在资源i的绿色部分，对于同一资源上和其他资源上的任何位置都不能再安排任务i。

式(4)表示每个任务的执行时间必须在可见时间窗口内，且满足相应的持续时间。

式(5)表示为了保证任务的时效性，每个任务必须安排在其规定的截止时间之前，比如虽然任务i在资源1、资源2及资源3上均有2个不同的时间窗口，但考虑到任务的截至期限，实际上，任务在各个资源上的有效时间窗口均只有一个，各个资源上位于任务的截至期限之后的时间窗口均为无效时间窗口。

式(6)表示在同一个卫星上相邻的2个被安排任务，必须满足相应的转换时间，以保证卫星有足够的时间完成姿态转换。

式(7)表示一颗卫星资源在同一时刻只能完成一个任务。

3 卫星任务动态调度优化算法

对地观测卫星动态调度问题实质是在满足各项约束条件的前提下，为各项任务合理分配卫星资源以及确定执行起止时间。虽然可以撤销原方案，利用整体重新规划调度的方法对所有的任务进行新的分配，理论意义上能得到全局最优解，但是这种方式没有充分利用原调度方案的优良特性，而且处理数据规模过大，无法满足时效性要求，并且产生的新调度方案对原调度方案干扰过大，不利于后续工作的开展。本文基于对地观测卫星任务安排中2个关键过程，即可见时间窗口的选取和执行时刻点的确定，给出了2种比较合理的启发因子，并将其加入了设计的基于启发式规则的ISR-HA算法。

3.1 启发因子设计

3.1.1 可见时间窗口拥挤度

可见时间窗口拥挤度，是指当将任务i安排在某个可见时间窗口后，对其他未安排新任务可能造成的干扰程度，以及对原调度方案中已安排任务干扰之和，计算公式如下：

(8)

式中，NT为新任务集中所有在衡量任务ti时还未安排的任务；OT为原调度方案任务集；λ为权衡对新任务和原任务干扰程度比重因子，根据需要进行调整，本方案中取λ=3。

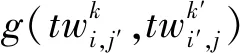
3.1.2 执行时刻点重叠度

每个任务都需要确定它的执行开始时刻和结束时刻，而每个任务的持续时间是一定的，那么只需要确定每个任务的开始时刻即可。若按照最早开始原则选择，有些情况会导致有些任务无法执行。如在同一个资源r上，若选择最早开始原则安排任务j，那么若后续任务i在该资源上的时间窗口也比较靠前，则将无法分配时间段执行观测。若按图3方式安排任务j，那么任务i和任务j均能得到安排。由此引入第二个启发因子，即执行时刻点重叠度。

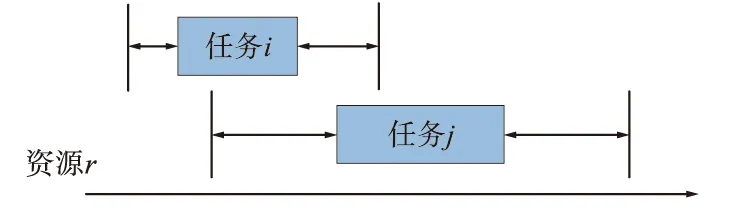
图3 按基于执行时刻点重叠度插入任务Fig.3 Insert task based on overlap of execution time

3.2 启发式ISR-HA算法设计

3.2.1 预处理

在预处理过程中，主要完成3大任务：

① 将动态调度时刻点以前的任务安排为已完成；② 删除动态调度时刻点以前的任务时间窗口；③ 删除不满足任务观测时长的时间窗口。

3.2.2 基于遗传算法的初始调度方案

在新任务动态插入之前，需要对原始任务集生成初始调度方案，在本文中使用遗传算法(GA)对原始任务集生成初始调度方案。具体流程包括编码设计—适应度函数设计，由于遗传算法比较成熟，本文不再赘述，需要强调的是：在编码设计中本文采用“卫星资源-时间窗次序编号”形式定义单个染色体，其示意如图4所示。

图4 动态调度遗传算法编码示意Fig.4 Diagram of genetic algorithm coding for dynamic sechduling

第1号任务分配给第4颗卫星的第2个可见时间窗口，第2号任务分配给第5颗卫星的第3个可见时间窗口，第3号任务分配给第1颗卫星的第4个可见时间窗口，第5号任务分配给第2颗卫星的第2个可见时间窗口。其中“0-0”表示第4号任务没有对应的卫星资源进行分配。

3.2.3 ISR-HA算法

ISR-HA算法步骤如下：

① 需要动态插入的新任务集合NewTasks中共有N个任务，将N个任务降序排列。

② 令i= 1。

③ 选择NewTasks集合中第i个任务，计算任务i每个可见时间窗口的拥挤度，并按非降序原则排列。

④ 按排序后的可见时间窗口顺序，依次考察每个可见时间窗口，计算该时间窗口内每个时刻点的重叠度，并按非降序原则排列。依次考察排序后每个时刻点，尝试无冲突的直接插空安排任务i，若成功，则转③；否则，转⑤。

⑤ 分别计算任务i插入到每个可选时刻点后，与任务i相冲突的已安排任务的数目。设任务i共有mi个可选时刻点，则得到任务i的任务冲突数向量ΔNi=[Δn1,Δn2,...,Δnmi]，并记录相应的任务冲突集，并按非降序排列ΔNi。

⑥ 依次从小到大考察ΔNi(为了保证对原调度方案扰动最小)，令k=1。

⑦ 选择Δnk，若k>mi， 则转⑧，否则将任务i安排到此时所选择的时刻点，将此时与任务i冲突的所有任务集移位，移位的原则是在不删除任何任务的前提下，将这些冲突任务重新安排。若成功，则转③;否则，恢复任务i插入前的状态，k=k+1，转⑦。

⑧ 分别计算ΔNi中每个相应任务冲突集的任务价值之和ΔWi=[Δw1,Δw2,...,Δwmi]，选择ΔWi中价值和最小的Δwk(为了保证最大化收益总值)，如果任务i的权值小于等于Δwk，表示任务i不能替代相应的冲突任务集，那么删除任务i，并将其加入任务集Delete，转③；否则，将相应的任务冲突任务集加入优先级队列Q中(Q的排序准则是按任务权值从小到大排序)。

⑨ 循环处理Q中每个任务，若队列为空则转⑩，否则取出队首元素j，若无冲突直接安排任务j成功，那么继续处理下一个队首元素；否则，找出与任务j冲突的最小权值任务集Δwj，若任务j的权值大于Δwj，那么任务j安排成功，并将与任务j冲突的任务加入Q中，继续处理下一个队首元素；否则删除任务j，并将其加入任务集Delete，继续处理下一个队首任务。

⑩ 若i≥N，转；否则i=i+1， 转③。

其中，关键步骤④任务直接插入过程的流程如图5所示。

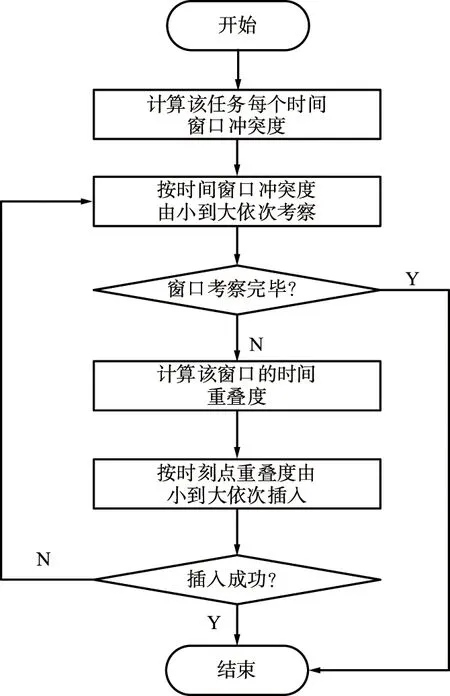
图5 任务直接插入流程Fig.5 Direct task insertion flow chart

其中步骤⑦任务移位插入过程示意如图6所示(插入任务k在不同执行窗口下的情况)。由此可知，如果要将动态任务k插入在资源r的执行窗口1，则此时与任务4及任务5在资源r上的执行时间窗口冲突，为了能够将动态任务k插入在资源r的执行窗口1上，此时必须将任务4及任务5的执行时间窗口在其可见时间窗口范围内移动到对应的虚线框内的时间段。同样，如果要将动态任务k插入在资源r的执行窗口2，则此时与任务1、任务2及任务3在资源r上的执行时间窗口冲突，为了能够将动态任务k插入在资源r的执行窗口2上，此时必须将任务1、任务2及任务3的执行时间窗口在其可见时间窗口范围内移动到对应的虚线框内的时间段。

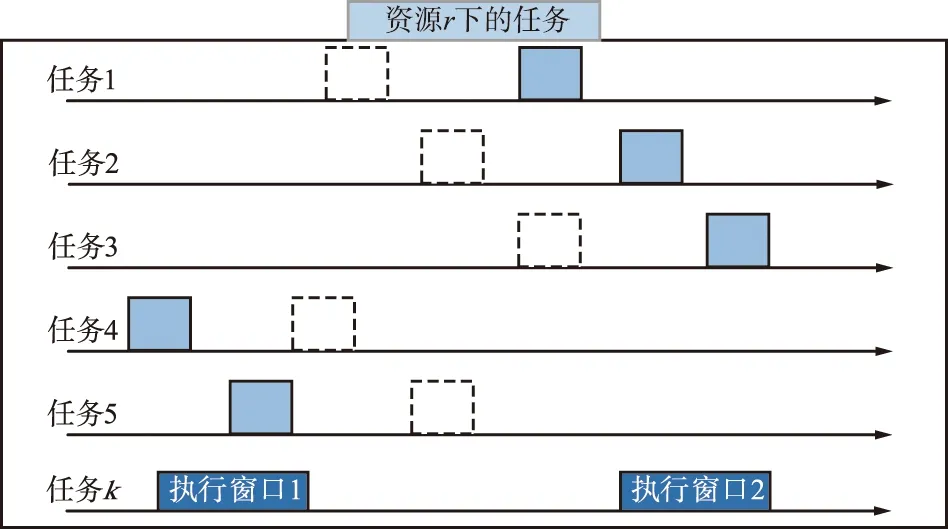
图6 任务移位过程图Fig.6 Task shift process diagram

综上，ISR-HA算法流程如图7所示。

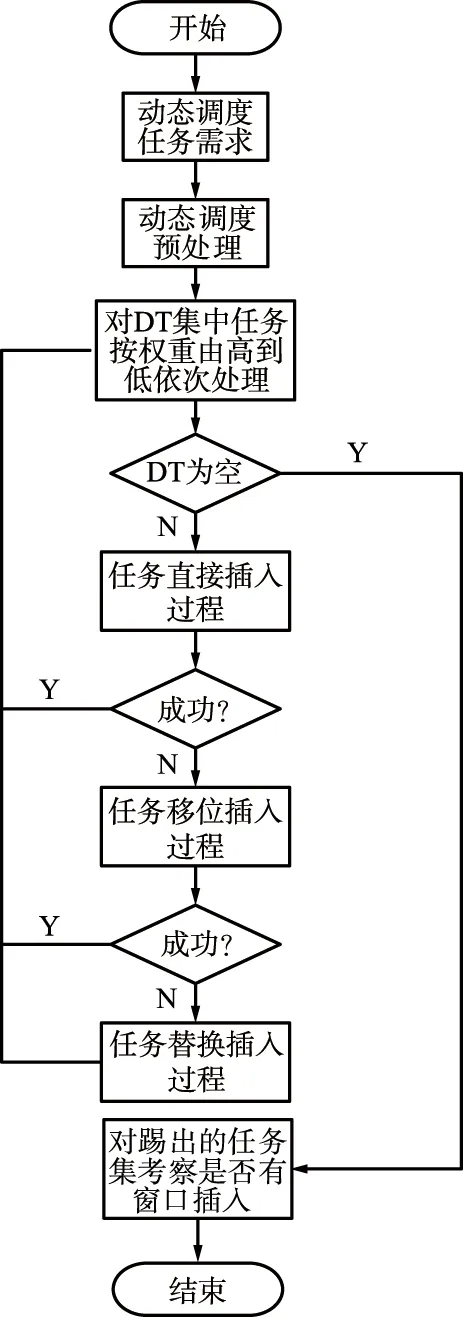
图7 ISR-HA算法流程Fig.7 ISR-HA algorithm flow chart

4 仿真实验

本次仿真实验环境为Core i7-8550 @1.8 GHz CPU，8 GB RAM，Windows 10，64位操作系统的笔记本电脑。设置仿真实验的 5颗卫星轨道参数，以及初始任务、新任务等相关基本参数，最后通过 Matlab R2016a 仿真对比验证所提出算法的有效性。

4.1仿真参数设置

实验的初始调度任务集数为150个，经度范围[76°E，131°E]，纬度范围[17°N，45°N]内随机生成的点目标任务;动态任务集数为200个，经度范围[80°E，120°E]， 纬度范围[20°N，42°N]内随机生成的点目标任务。实验通过卫星工具包(STK)生成相应的卫星观测任务集，动态任务集的经纬度范围更集中，有利于增加与原任务集的时间冲突度。仿真实验总调度周期设置为24 h(2020年5月15日0:00-24:00)，动态调度时刻点设置为2020年5月15日6:00。

仿真实验卫星轨道基本参数设置如表1所示。

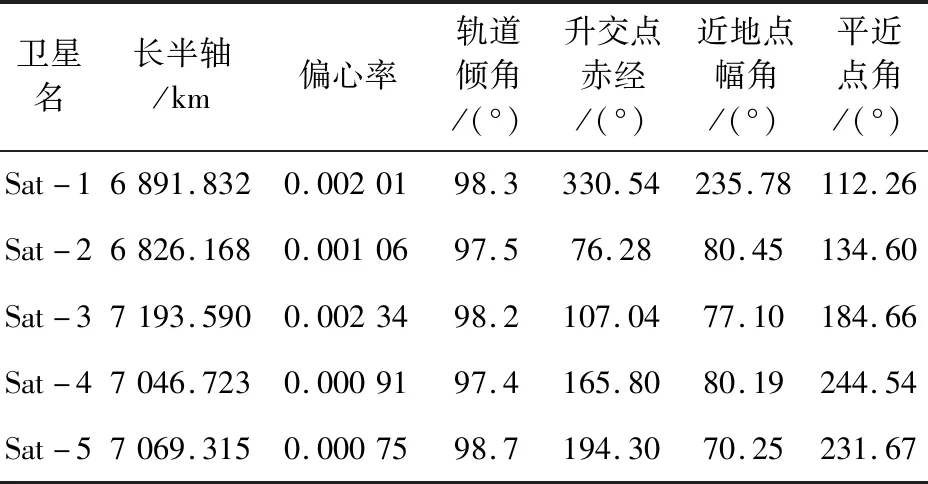
表1 仿真实验卫星轨道基本参数表Tab.1 Basic paramaters of simulation experimental satellite orbit

4.2 仿真实验及结果分析

通过前一节设置的任务观测集数据和卫星轨道参数即可获得每个观测任务的卫星过境窗口来进行卫星观测任务的调度。由于反应式调度基于初始预调度进行重新调度，仿真实验首先采用GA对初始任务集生成初始预调度方案，生成的初始调度方案如表2所示。

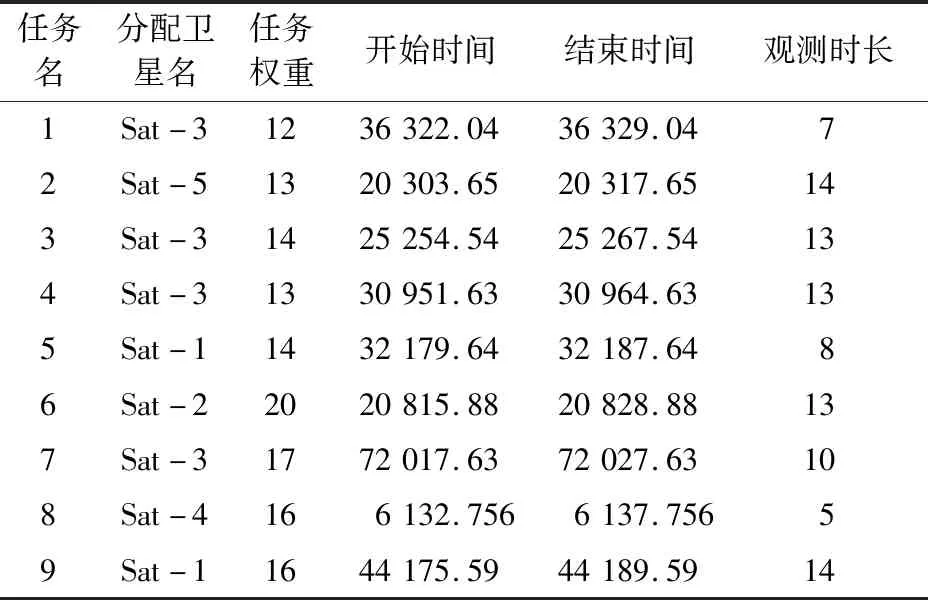
表2 仿真实验初始调度方案(部分)Tab.2 Initial schedule scheme of simulation experiment (partial) 单位：s

为了验证启发因子本身设计的有效性，本文从2种设计的算法中分别加入和不加入启发因子2种情况进行对比，为了方便对以下实验结果管理，做以下名称替换：

(a) 表示未加任何启发式策略的改进迭代法；

(b) 表示加了时间窗口拥挤度，以及基于重叠度的开始执行时间启发因子的改进迭代法；

(c) 表示没有加入任何启发因子的ISR-HA算法；

(d) 表示在直接插入过程、移位插入过程和替换插入过程中均加入了两种启发因子的ISR-HA算法。

通过设置动态任务集的个数(10、20、100和200)来对上述各个算法分组仿真，为避免少数实验的随机性造成的影响，本文将每种算法迭代 10 次，得到的卫星调度结果如表3所示。

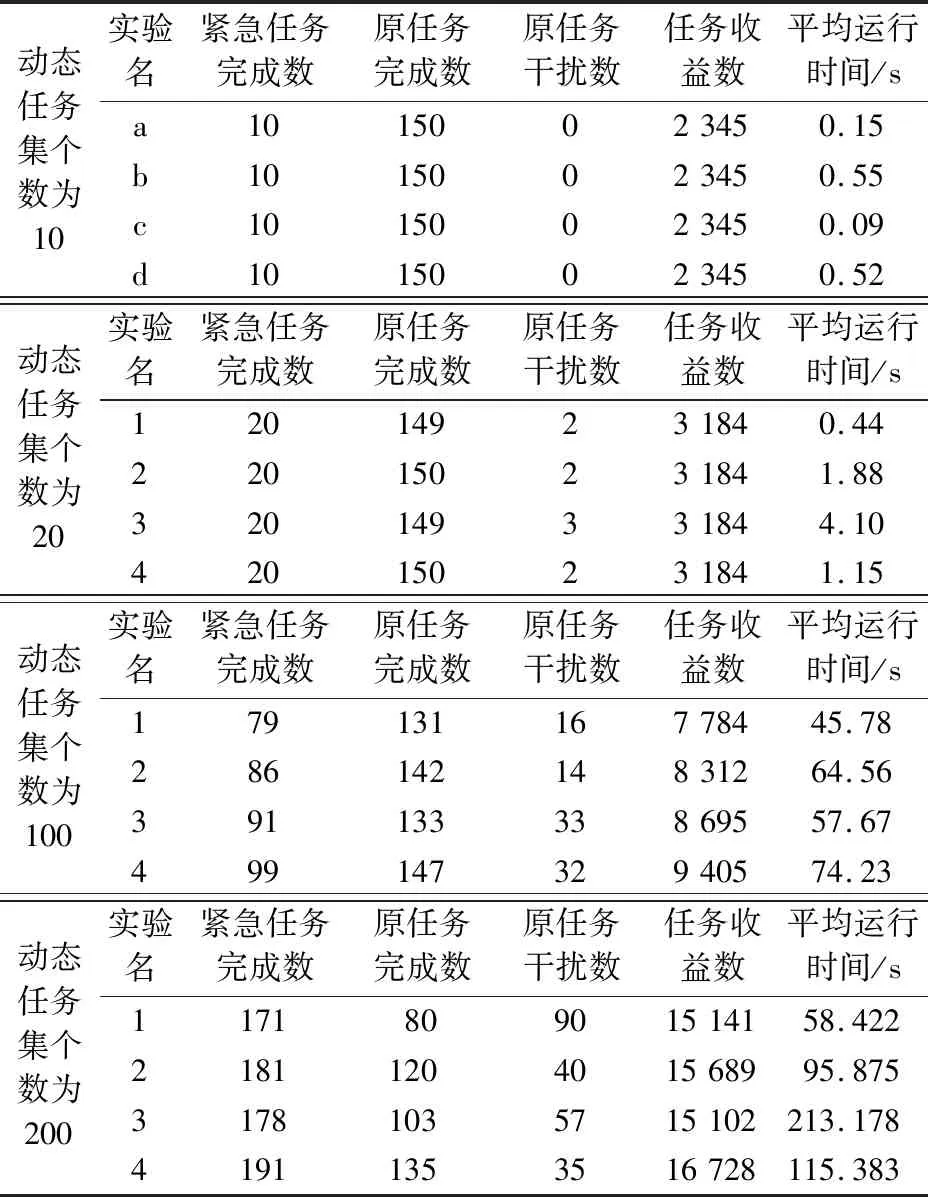
表3 各算法动态插入任务规划仿真实验结果表Tab.3 Simuliation experiment result of dynamic insertion of algorithms into a task planning

以任务收益和扰动测度作为最后对比的参考结果，具体结果如图8所示。

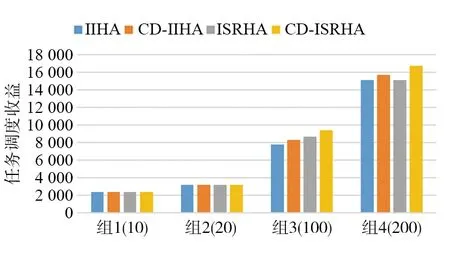
图8 4种算法任务调度收益对比Fig.8 Comparision of task scheduling benefits among four algorithms

由图8可以看出，当动态任务集个数较少时(个数为10和20)，紧急任务集与已安排任务集冲突度较小，4种算法都能完成已安排任务和动态任务集，无观测收益上的差别；当动态任务集个数较多时(个数为100和200)，紧急任务集与已安排任务集冲突度较大，ISR-HA算法的观测收益要高于II-HA算法的观测收益，其中ISR-HA比II-HA平均收益提高5.8%，并且加入2种启发式因子的算法与不加启发式因子的算法对比，明显有观测收益上的提高，其中II-HA和ISR-HA的平均收益分别增加5.2%和9.5%，证明了本研究2种启发因子的有效性。4种算法任务扰动测度对比如图9所示。

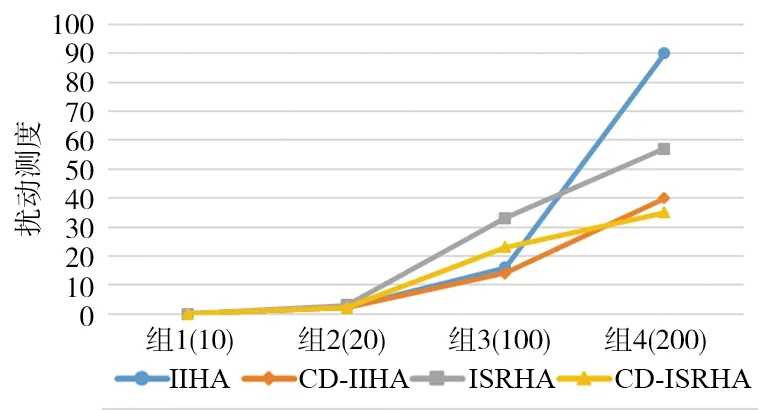
图9 4种算法任务扰动测度对比Fig.9 Comparision of task disturbance measures among four algorithms

由图9可以看出，当动态任务集个数较少时(个数为10和20)，紧急任务集与已安排任务集冲突度较小，4种算法都能完成已安排任务和动态任务集，在任务扰动测度上无明显区别；当动态任务集个数较多时(个数为100和200)，紧急任务集与已安排任务集冲突度较大，II-HA算法的扰动测度起初低于ISR-HA算法的扰动测度，但随着冲突度的增加，II-HA算法的扰动测度迅速增加并远远超过ISR-HA算法的扰动测度，另外加入2种启发式因子的算法与不加启发式因子的算法对比，明显有扰动测度上的降低，其中II-HA和ISR-HA的平均扰动测度下降34%和34.4%，证明了本研究2种启发因子的有效性。

5 结束语

卫星对地观测任务规划问题已经被证明是NP-Hard问题。本文针对卫星任务规划调度的动态调整需求，将所有的任务划分为已完成任务、已安排任务和新任务。第一步，对卫星任务动态调度问题进行统一描述，包括新任务的插入、已安排任务的取消、任务优先级的变更、天气条件的变化和卫星资源状态的变化描述为新任务的插入；第二步，以最大任务收益和最小任务扰动测度为目标函数构建完成任务动态调度优化模型，设计可见时间窗口拥挤度和执行时刻点重叠度2种启发式因子；最后，提出基于启发式智能ISR-HA算法寻求最优任务编排结果。