基于深度神经网络的京津冀地区PM2.5反演

刘 宇,楚博策,高 峰,邓 越

(1.中国电子科技集团公司航天信息应用技术重点实验室,河北 石家庄 050081；2.北京师范大学 地理科学学部,北京 100875)

0 引言

PM2.5是指空气动力学当量直径≤2.5 μm的颗粒物，其在空气中的浓度越高，则意味着空气污染越严重。已经有研究指出，人体某些病症的发生概率与人在污染空气中的暴露时间呈正相关[1-2]。随着近年来中国北方雾霾天气的频繁发生，尤其是京津冀地区，社会对PM2.5的分布情况越来越关注[3]。地面PM2.5浓度的监测及实时公布已经成为环境领域的重要内容。传统的PM2.5监测方式是地面站点监测,“十二五”以来，已经在全国建立了空气质量监测网，但是监测站点基本上集中在城市地区，且全国总共只有1 497个监测站点。站点数量严重不足以及空间分布不均导致难以在面尺度上进行全国PM2.5监测[4]。

低分辨率遥感能够获得大范围的大气观测信息，且拥有较高的时间分辨率，能够满足对PM2.5进行时间和空间上的连续观测，所以近些年已有很多研究人员使用遥感进行不同地区的PM2.5反演[5-7]。根据PM2.5反演方法的差异，可以将这些PM2.5反演模型分为2类：基于模拟和基于卫星观测数据的模型。基于模拟的模型通常使用全球化学传输模型来刻画气象因子和气溶胶对PM2.5浓度的影响效应，然后将建立的模型应用到卫星观测数据，来反演PM2.5浓度[8-9]。该类模型的缺点是对数据要求较高，且化学传输模型需要较多的参数设定。基于卫星观测数据的模型是遥感领域较为通用的模型，其基本原理是基于PM2.5浓度和气溶胶光学厚度(AOD)间的统计关系。该模型是遥感领域较为常用的方法，优点是所需数据教少，且方法简单[10]。利用地理加权回归算法建立MODIS AOD数据与PM2.5浓度的统计关系，并考虑气象因子在模型中的有效性，该模型的精度明显优于多元线性回归模型[11]，Ma等[12]则同时考虑了气象因子和土地利用情况对PM2.5反演的影响。杨丽娟等[13]认为虽然气象因子和土地利用情况等参数对AOD和PM2.5间的模型建立有积极影响，但气象因子的变化较复杂，会导致AOD和PM2.5浓度间呈现明显的日差异关系，故建立了包含固定效应和随机效应的日校正模型。考虑到PM2.5和AOD数据间具有时空变异的统计特性后，有研究人员尝试使用2层统计模型来分别对PM2.5-AOD在时间和空间上的变异进行建模[14-16]。半经验模型是另外一种较常用的PM2.5反演模型，该模型考虑的因子与上述模型并无差别，只是一般使用指数函数形式进行气象因子和PM2.5间的回归[7,17-18]。

传统的回归模型能够通过有限样本刻画简单的映射关系，但实际应用中，数据量的增加会给回归模型带来巨大挑战。当因变量与自变量间是复杂的非线性映射关系时，如PM2.5浓度与气象因子、AOD间呈难以简单描述的非线性关系，传统的回归模型很难对样本进行准确建模[19]。而深度神经网络(DNN)能够有效学习样本中的复杂非线性映射关系，对噪声数据有较好的鲁棒性，非常适用于PM2.5反演的建模。

京津冀地区是我国雾霾发生最频繁以及最严重的区域，监测京津冀地区及其周边PM2.5的时空分布可为环境部门提供决策支撑。当前，使用深度学习进行PM2.5反演建模的研究还很少；为此，本文使用MODIS AOD数据，并结合气象同化资料，利用DNN挖掘PM2.5和气象因子、AOD间的非线性关系，构建PM2.5反演模型，并依此分析PM2.5的时空分布模式。

1 研究区和数据介绍

1.1 研究区概况

京津冀地区是我国空气污染最严重的地区之一，根据环保部的数据显示，2016年京津冀区域大气优良天数比例为56.8%，比全国平均天数比例低22%。京津冀大气污染严重的原因主要有2个：其一，京津冀地区是重化工业集中的重要区域，集中了多种废气、废水排放，从而直接影响大气质量的产业，其中以钢铁产业为主，包括船舶、水泥等重污染产业；其二，京津冀地区地形复杂，西邻太行山脉、北靠燕山山脉、东邻渤海，再考虑到京津冀地区的海陆风转换情况，京津冀地区的大气污染物难以疏散[20]。

随着社会对大气污染问题的重视程度逐渐提高，国家相继出台了若干细则进行京津冀地区的大气污染整治。为及时评估大气污染整治情况，有必要及时对京津冀地区PM2.5的时空分布进行长期监测。

1.2 数据介绍

本文使用的数据包括2015年中国环境监测总站发布的PM2.5站点数据、MODIS AOD气溶胶产品数据以及再分析气象资料MERRA-2。

1.2.1 PM2.5站点数据

2013年开始，中国环境监测总站在全国338个地级以上城市设置空气质量监测站点1 436个，“十二五”期间，又建成了农村区域空气质量监测站点61个。目前，中国环境监测总站实时公布1 497个监测站点的监测数据(包括PM2.5、PM10、NO2、SO2、O3、CO浓度)。该数据为遥感反演面尺度的PM2.5浓度提供了数据基础。

由于单一省份内空气质量监测站点数量较少，且地理分布不均匀，会导致深度学习样本过少，故本研究使用包括北京市、天津市、河北省及其周边共9个省市的空气质量监测站点数据，以增加样本数量。提取2015年1月1日—12月31日的PM2.5逐小时数据，并求取10—11时的PM2.5浓度平均值，以对应MODIS上午的过境时间10:30。

1.2.2 MODIS AOD产品

MOD/MYD04(MODIS Terra/Aqua Aerosol)产品是NASA发布的Level 2级气溶胶产品，用来获取全球海洋和陆地的大气气溶胶光学特性(如AOD等)。在之前的Collection 5中，NASA仅提供了10 km分辨率的气溶胶产品，而在最新的Collection 6中，NASA提供了3 km分辨率的气溶胶产品。本文使用2015年每天的MOD/MYD AOD产品，空间分辨率为3 km。

Terra星过境时间大约在10:30，Aqua星过境时间大约在13:30，故MOD04 AOD产品和MYD04 AOD产品分别对应的是10:30和13:30的AOD数据。由于该产品中部分像素值缺失，故本文使用回归方式对缺失值进行补充[21]：将每天的MOD04 AOD和MYD04 AOD数据进行线性回归，然后利用该回归方程进行MOD04 AOD缺失值的补充。

1.2.3 气象数据MERRA-2

本文使用NASA发布的MERRA-2再分析产品，该产品使用GEOS-5同化系统生成，空间分辨率为0.625°×0.5°，包括自1981年至今的气象再分析资料。提取京津唐地区2015年每日10时的地表气压、2 m高相对湿度、2 m高气温数据，行星边界层高度数据以及地表风速数据用于本研究的建模(GMAO,2015)。

将以上数据处理为时间和空间上统一的数据集。首先，将AOD数据和气象数据重投影到地理坐标系下，分辨率为0.03°；然后，提取对应空气质量监测站点位置的AOD和气象数据，考虑到空气质量监测站点和其他数据间的地理定位误差，使用3×3窗口像元平均值为对应空气质量监测站点的AOD和气象数据。最后，删除无观测值记录，共得到32 753条记录用来发展PM2.5反演模型，每条记录包括PM2.5浓度、AOD、相对湿度RH、地表气压SP、气温T、行星边界层高度PBLH及地表风速SWS。

2 PM2.5浓度反演方法

2.1 样本均衡化

PM2.5浓度天数呈伽马分布如图1所示，污染主要集中在低于100 μg/m3的区域，PM2.5浓度高的天数非常少，浓度极高的天数趋近于0。不均衡的样本分布会导致DNN模型训练的时候难以捕获PM2.5高值区的特征[22]，故需要对样本进行均衡化处理。

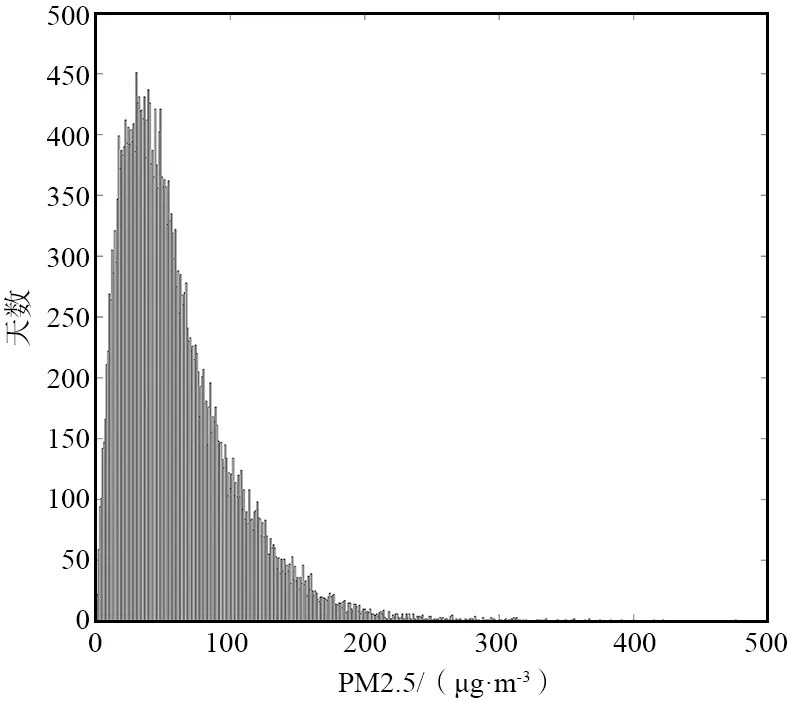
图1 2015年研究区内所有空气质量监测站点每日10时PM2.5浓度天数分布Fig.1 Daily distribution of PM2.5 concentrations at 10 a.m.observed by all air quality monitoring systems in the study region in 2015

本文使用传统的重复过采样方法进行样本均衡化。假设样本集中PM值为i的天数为Ni，首先确定Ni的最大值Nmax，然后将Ni小于Nmax的样本复制至Nmax个，使PM浓度值呈均匀分布。

2.2 深度神经网络结构及其评估方法

将均衡化的样本按照0.9∶0.1的比例划分为训练样本与检验样本；根据训练样本与检验样本不断调整DNN的结构参数，包括隐藏层数量和每层的节点数量，得到的最优结构如图2所示。该DNN共有8个隐藏层，每层的隐藏节点个数分别为39,31,27,21,15,11,7,3。

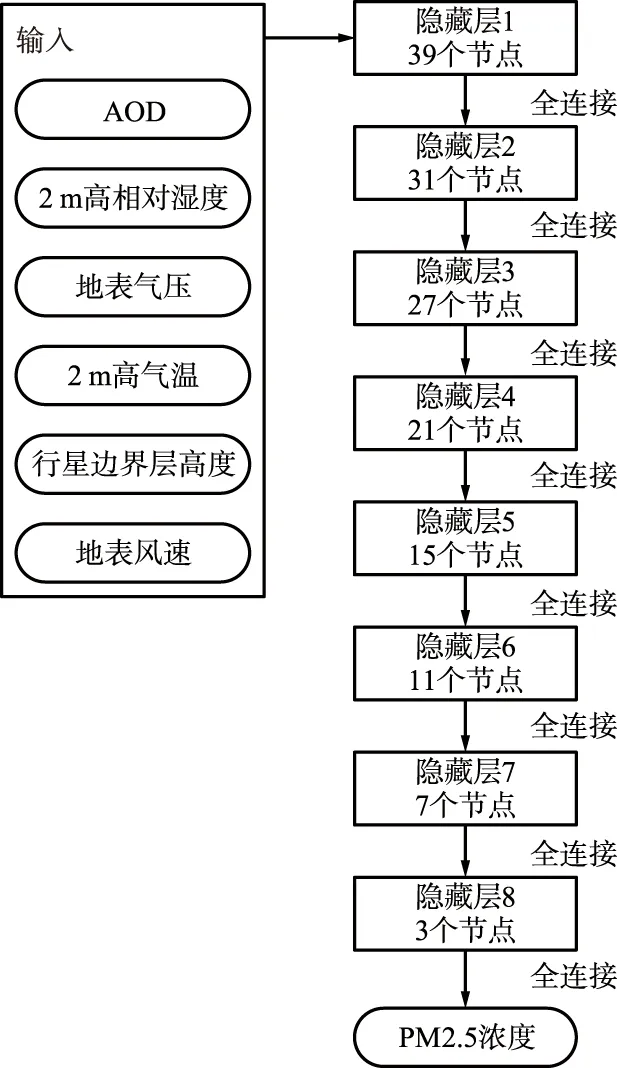
图2 拟合效果最优的深度神经网络结构Fig.2 Structure of DNN obtaining optimal fitting result

作为对比，使用式(1)的半经验回归模型对样本进行回归验[18]：

ln(PM2.5)=β0+βAODln(AOD)+βPBLHln(PBLH)+

βRHln(RH)+βTln(T)。

(1)

对该模型的评估指标包括相关系数r(PM2.5真实值与模型值间的相关系数)、平均绝对误差MAE以及平均相对误差MRE。

2.3 基于点面融合模型的PM2.5时空数据融合方法

由于AOD数据缺失，导致DNN反演得到的PM2.5分布也是缺失的，本文采用点面融合模型对PM2.5的时空分布进行插值[21]。空气质量监测站点的PM2.5浓度数据不包含空间特征，但其反映的时序规律是准确的，而DNN反演的PM2.5浓度数据则包含部分准确的空间特征；点面融合模型结合了站点插值数据与DNN反演数据的优点，该模型假设站点插值PM2.5数据在不同日期间的差值与DNN反演的PM2.5数据在相同日期间的差值相同，具体方法为：

Vi,j,t1-Vi,j,t2=Mi,j,t1-Mi,j,t2，

(2)

式中，i,j代表像素位置(行、列值)；t代表时间(天)；V为DNN反演的PM2.5浓度数据；M为PM2.5站点插值数据。假设Vi,j,t1为PM2.5浓度缺失值，Vi,j,t2为时间上距离Vi,j,t1最近的有效值，则其差值与PM2.5浓度在站点插值数据中的差是相同的。

3 结果与讨论

3.1 样本均衡化的效果

原始样本数量为32 753个，经过样本均衡化后的样本数量为148 330个。对原始样本同样按照0.9∶0.1的比例进行DNN的训练和检验，得到拟合效果最优的网络结构与图2相同。作为均衡化样本的对比，表1列出了原始样本与均衡化样本的拟合结果。

表1 DNN模型对原始样本与均衡化样本拟合效果对比Tab.1 Comparison between fitting result for original samples and balanced samples separately on DNN model

原始样本的拟合相关系数0.43远低于均衡化样本的拟合精度0.94；同时由于原始样本分布过于集中，导致训练样本集与检验样本集的拟合效果相差较大，训练样本集的拟合相关系数为0.68，而检验样本集的拟合相关系数仅为0.43。原始样本与均衡化样本拟合结果的MAE差异不大，但由于原始样本分布过于集中，其训练样本集与检验样本集的MAE差异更大；原始样本中训练样本集与检验样本集拟合结果的MRE差异巨大，达到20.6%。

作为对比，均衡化样本的拟合结果远远优于原始样本，同时训练样本和检验样本在模型拟合精度上差异也明显优于原始样本，MAE差异仅为0.5 μg/m3，MRE差异仅为0.3%，故样本均衡化明显提高了DNN模型的鲁棒性和PM2.5反演时的精度。

3.2 PM2.5回归精度

使用图2的DNN模型分别对训练样本集和检验样本集进行拟合，拟合结果如图3所示。对训练样本集而言，真实PM2.5浓度与模型预测的PM2.5浓度间的相关系数为0.944，平均绝对偏差为24.5 μg/m3，平均相对偏差为25.9%；对于检验样本集而言，真实PM2.5浓度与模型预测的PM2.5浓度间的相关系数为0.94，平均绝对偏差为25.0 μg/m3，平均相对偏差为26.2%，DNN对训练样本集和检验样本集的回归散点图如图3所示。

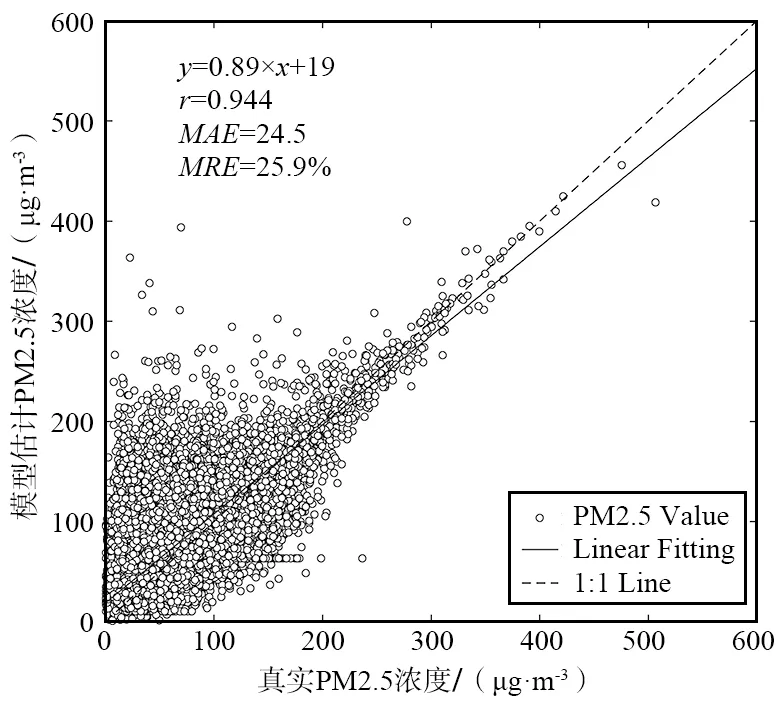
(a) 训练样本集的拟合结果

半经验回归模型对训练样本集和验证样本集的集合结果如表2所示，回归相关系数仅为0.18，远低于DNN模型的0.94；平均绝对误差和平均相对误差也远高于DNN模型的结果。

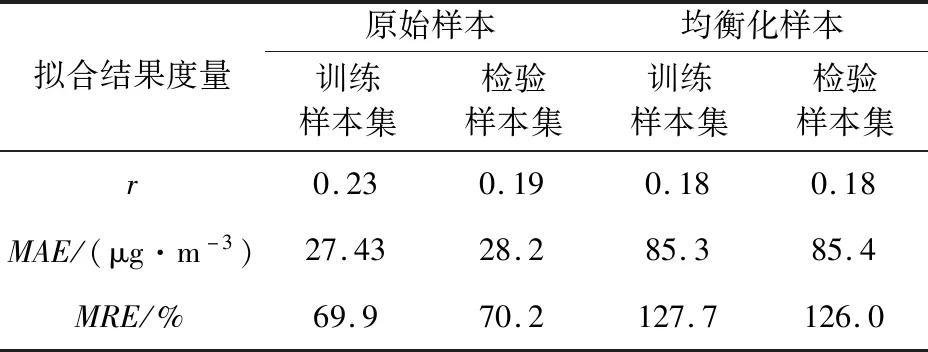
表2 半经验回归模型对原始样本与均衡化样本拟合效果对比Tab.2 Comparison between fitting result for original samples and balanced samples separately onsemi-empirical model

3.3 PM2.5时空分布

利用点面融合算法，可以得到每天上午10:30空间分辨率为0.03°的PM2.5时空分布；考虑到在气象条件不发生较大变化的情况下，PM2.5浓度不会发生剧烈变化，故上午10:30的PM2.5浓度可以一定程度上代表全天的PM2.5浓度。本文假定每日10:30的PM2.5浓度为日均PM2.5浓度，全月每日10:30的平均PM2.5浓度为月均PM2.5浓度，全年每日10:30的平均PM2.5浓度为年均PM2.5浓度。

DNN反演得到的月均PM2.5时空分布如图4所示。

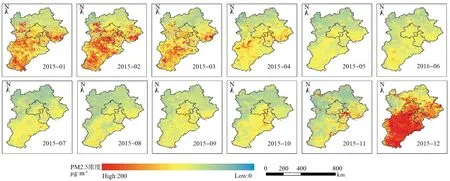
图4 DNN模型反演的京津冀地区2015年月均PM2.5浓度时空分布图Fig.4 Spatiotemporal distribution of average PM2.5 concentration monthly in Beijing-Tianjin-Hebei area retrieved by DNN model

从时间上看，PM2.5浓度较高的月份主要集中在属于冬季的12月、1月和2月，这与实际情况相符，每年冬季由于京津冀地区供暖的需求，煤炭燃烧会向大气输送大量污染物，同时，受蒙古西伯利亚高压控制，大气污染物不易扩散；PM2.5浓度最低的月份为9月。

PM2.5浓度年均地理分布如图5所示。PM2.5浓度较高的地区集中在北京市中部以南地区，太行山东部，与实际情况相符，受到地形因素影响，京津冀地区西侧毗邻太行山，北京北部山地环绕，导致大气污染物难以扩散；京津冀北部空气质量为优良状况。

(a) 空气质量监测站点插值数据 (b) DNN模型反演数据图5 PM2.5年平均空间分布Fig.5 Annual average geographical distribution of PM2.5 concentration

作为京津冀地区空气污染严重且最受关注的城市，北京市与石家庄市PM2.5浓度的逐日波动如图6所示。

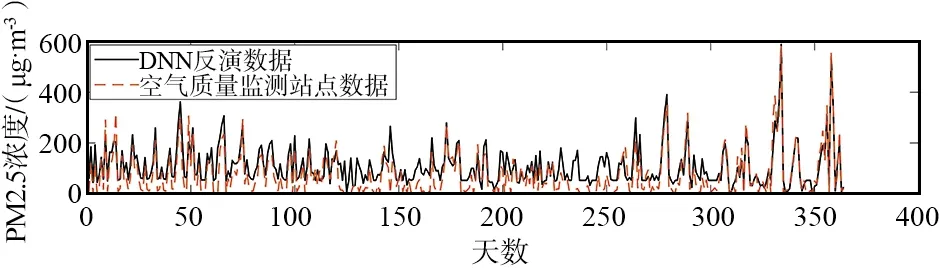
(a) 北京市

对于北京市，DNN反演的11、12月份PM2.5浓度与空气质量监测站点数据一致性很好，但其他日期的数据间存在系统偏差；对于石家庄市，DNN反演的全年PM2.5浓度与空气质量监测站点间数据一致性都很好。北京市全年的空气污染波动频率较均匀，PM2.5浓度峰值主要分布在冬季，最高值可达589 μg/m3；12月份的空气污染频率略低于其他月份，但大气污染的持续时间长于其他月份，年平均PM2.5浓度为107.3 μg/m3。石家庄市呈现出与北京市相同的空气污染波动模式，PM2.5浓度峰值同样主要分布在冬季，但峰值395 μg/m3低于北京市，但年平均PM2.5浓度110.5 μg/m3略高于北京市；同时，石家庄市冬季高污染的频率也高于北京市。

4 结束语

本文使用MODIS AOD数据及MERRA2气象再分析资料构建了PM2.5浓度反演的DNN模型，验证了该模型在PM2.5浓度反演方面的效果，通过样本均衡化的方法提高了DNN在反演PM2.5浓度时的精度，并用此模型反演了2015年京津冀地区的PM2.5浓度时空分布。最后，通过月均PM2.5浓度空间分布、年均PM2.5浓度空间分布及北京市与石家庄市PM2.5日波动情况进行了初步分析。得到相关结论：① 样本均衡化增加了PM2.5高值的样本数量，使得样本分布更加均一，有效地将DNN的拟合相关系数由0.43提高到了0.94，且增加了DNN模型的鲁棒性。DNN模型对PM2.5浓度站点数据的拟合相关系数分别为0.944和0.94，平均绝对误差和平均相对误差分别为25.0 μg/m3，26.2%，完全能满足对京津冀地区大气污染监测的需要。② 京津冀地区的大气污染主要分布在中南部，且中南部的污染程度远高于北部地区；2015年，京津冀地区大气污染最严重的时间为冬季，夏季的PM2.5浓度最低，北京市与石家庄市PM2.5浓度峰值均分布在冬季；北京市与石家庄市12月份的空气污染频率略低于其他月份，但大气污染的持续时间长于其他月份。