基于概率统计的水电机组状态监测参数波动预警策略
周宁刚,徐剑峰,江书樵,陈泽阳
(1.浙江华电乌溪江水力发电有限公司,浙江省衢州市 324000;2.北京华科同安监控技术有限公司,北京市 100043)
0 引言
自20世纪90年代起,水电机组状态监测系统陆续在各大水电厂投运,至今已得到广泛应用,实时监测水电机组的振动、压力脉动、噪声等特征参数,当出现异常时及时做出预警,保障水电机组的安全运行[1]。近年来,行业内对水电机组状态监测数据开展了多种数据挖掘研究,探索更完善、更科学的预警模式。参考文献[2]对某机组在一定时段的不同监测值进行了概率统计,证明了不同监测值的概率分布与正态分布较为接近。参考文献[3]对机组轴瓦温度进行了统计分析,并进行了严格的分布检验,证明了轴瓦温度数据的样本均值序列服从正态分布。参考文献[4]和参考文献[5]对比了不同的概率统计方法对状态监测数据统计特性的影响。参考文献[6]对基于不同统计原理的故障诊断方法做了梳理和对比。参考文献[7]设计了基于机器学习的水电机组监测参数预警模式。但时至今日,状态监测系统的预警方式仍多以单一的限值作为预警依据,即当实时监测值超过预设的阈值时做出预警。对此,本文根据正态分布理论,对状态监测参数的波动特性开展统计分析,探寻机组潜在的状态变化,进而对其波动中出现的异常进行预警,以期改善单一阈值的越限预警方式,提高水电机组的安全运行系数。
1 波动预警原理
水电机组属于慢速旋转机械,运行特性经常处于缓慢变化的状态,在系统工作正常的前提下,监测参数较少出现突然跳变的情况。若机组由于某种故障或潜在隐患的不断恶化,运行状态已在发生缓慢的劣化,但监测参数尚未超过预设的阈值,此时单一阈值的预警方式难以察觉。此外,水电机组监测参数的单一预警限值大多来自于相关国内、国际标准中对应的规定,即便设置了多个单一阈值进行分级报警,仍为单一的数值越限预警模式,不能监测到特征参数正在发生的缓慢变化。这就导致故障已经发生或设备已恶化到一定程度才被发现,给机组的安全运行带来隐患,增加未预期的检修成本。
根据概率统计学中的中心极限定理,对于容量足够大的数据样本,其采样均值服从正态分布[8],可利用正态分布的理论对其进行分析。
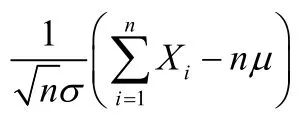
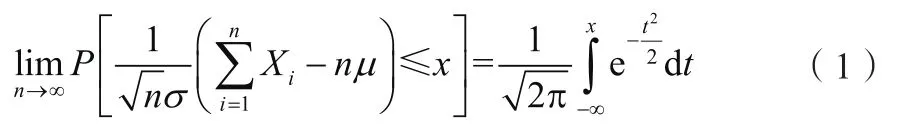
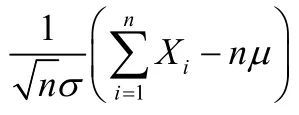
中心极限定理表明,只要采样样本容量n足够大,多次采样的样本均值序列服从正态分布。对水电机组而言,特征参数的每一个实时监测值由系统根据实时采集波形独立计算得出,不同的监测值之间相互独立,且由于其监测同一特征参数,不同的监测值服从同一概率分布。不管该概率分布为一明确的还是未知的数学分布,其均值序列均应服从正态分布。但值得注意的是,中心极限定理表述的是监测值的样本均值序列服从正态分布,而非不同监测值构成的序列本身服从正态分布。因此,不可盲目地对任一监测参数的数据序列进行概率统计分析,即便其近似服从正态分布,也属偶然现象,且缺乏中心极限定理的理论支持,必须经过严格的正态分布检验,才可利用正态分布的理论进行分析。
根据中心极限定理,若某一监测参数的采样样本均值序列服从正态分布,即可对该参数n次采样的均值进行监测和预警。由于监测参数的均值反映的是该参数在稳态工况下的缓慢波动,本文定义该预警模式为波动预警。具体而言,根据正态分布的理论,监测参数实时值位于3σ区间内的概率为99.74%,即99.74%的概率下,监测值会在3σ区间内波动,如果数据波动超出了这一区间,监测参数出现异常的概率为99.74%。因此,可采用3σ准则设定参数的波动阈值:

式中:μ——样本均值;
σ——样本标准差。
2 波动预警的实现
选取国内某水电机组满负荷稳定运行10h积累的监测数据进行概率统计分析,包括上导摆度+X、上机架水平振动+X、蜗壳进口压力脉动、发电机层噪声4个监测参数。状态监测系统每3s保存一组实时数据,以上每个监测参数分别包括12000个数据点,作为统计分析的总体P。
2.1 概率特性统计
4个监测参数的时域分布如图1所示。从图中可以看出,由于机组在满负荷稳定运行,各监测值均保持稳定,偶有数值出现突然增大或减小的现象,但未超过系统预设的单一报警阈值,系统不会作出预警。
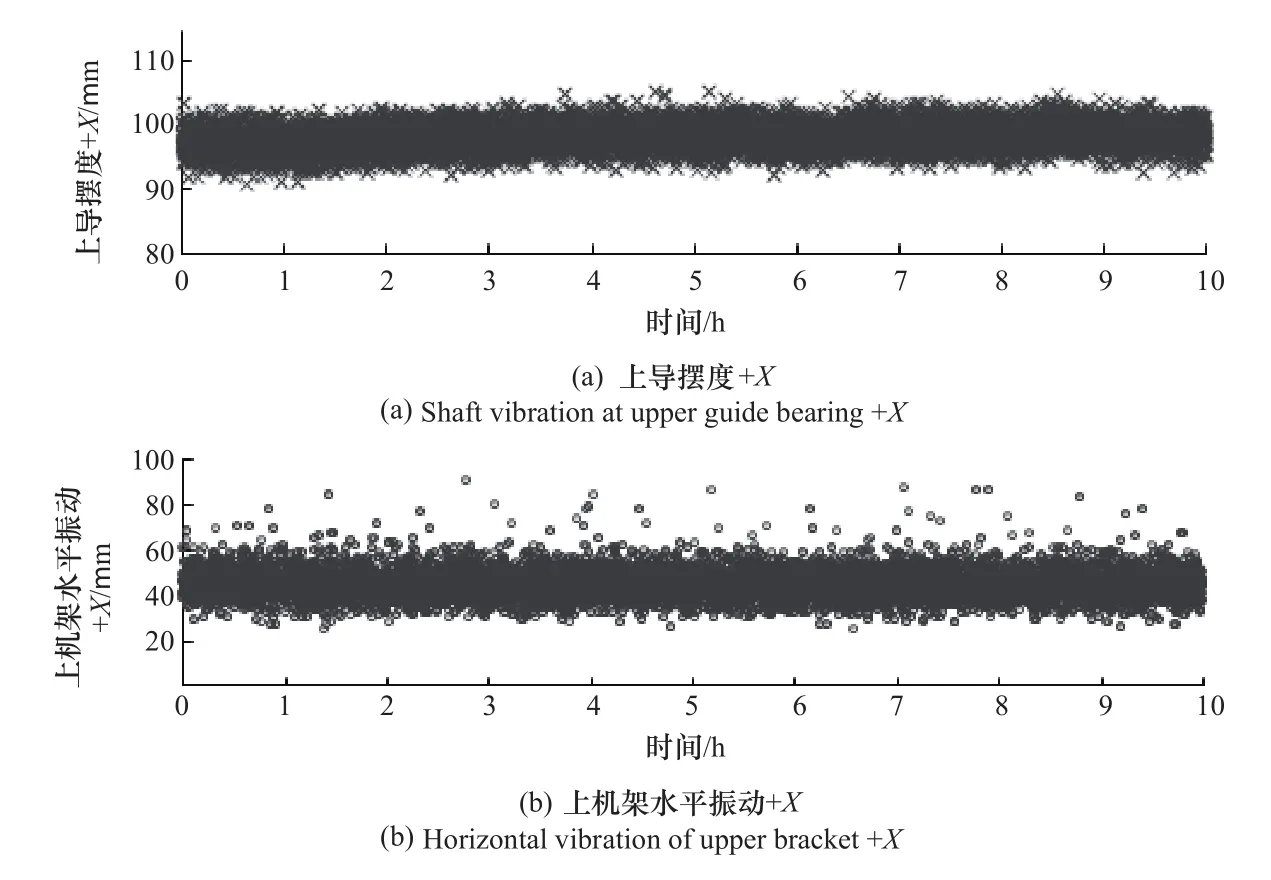
图1 监测参数时域分布图(一)Figure 1 Time-domain diagrams of monitoring parameters(No.1)
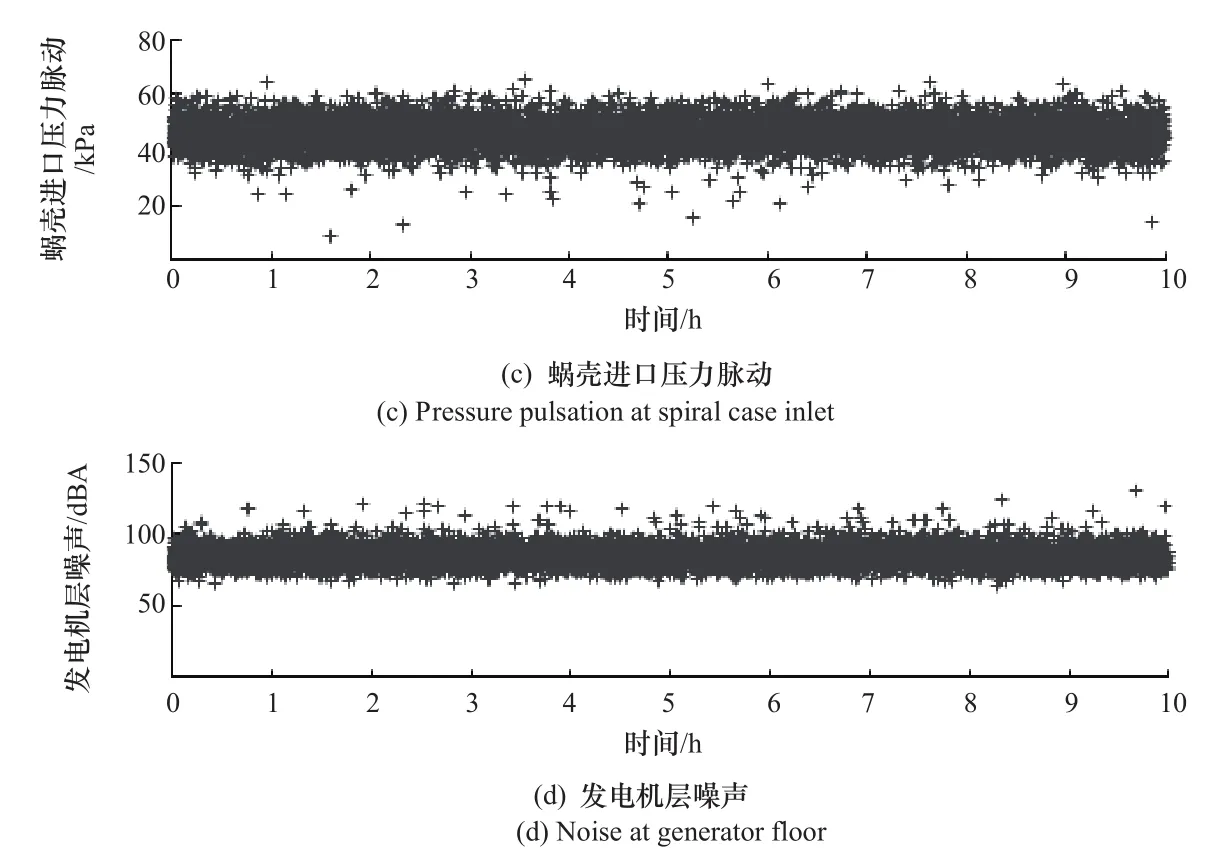
图1 监测参数时域分布图(二)Figure 1 Time-domain diagrams of monitoring parameters(No.2)
2.2 数据分布验证
对每个监测参数,按照以下步骤进行数据分布检验:
(1)在总体P中进行n次采样,得到n个样本值x1,x2,…,xn,计算样本均值;
(3)利用MATLAB中的Jbtest函数对样本均值序列进行正态分布检验。
4个监测参数的概率密度分布如图2所示。累积概率分布如图3所示。从图2和图3可以看出,监测数据的概率分布近似服从正态分布。正态分布检验结果如表1所示。
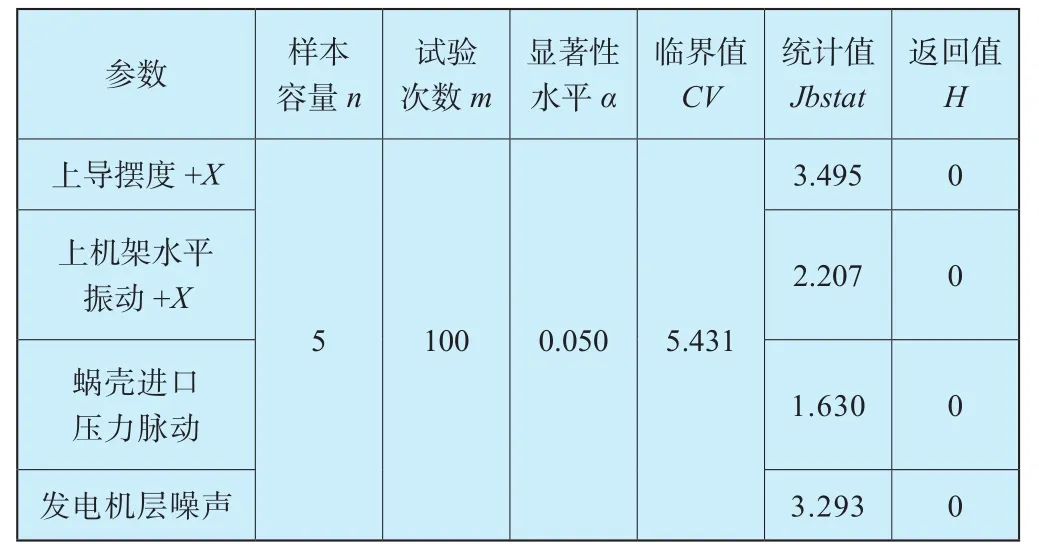
表1 监测参数正态分布检验结果Table 1 Test results of Gaussian distribution on monitoring parameters
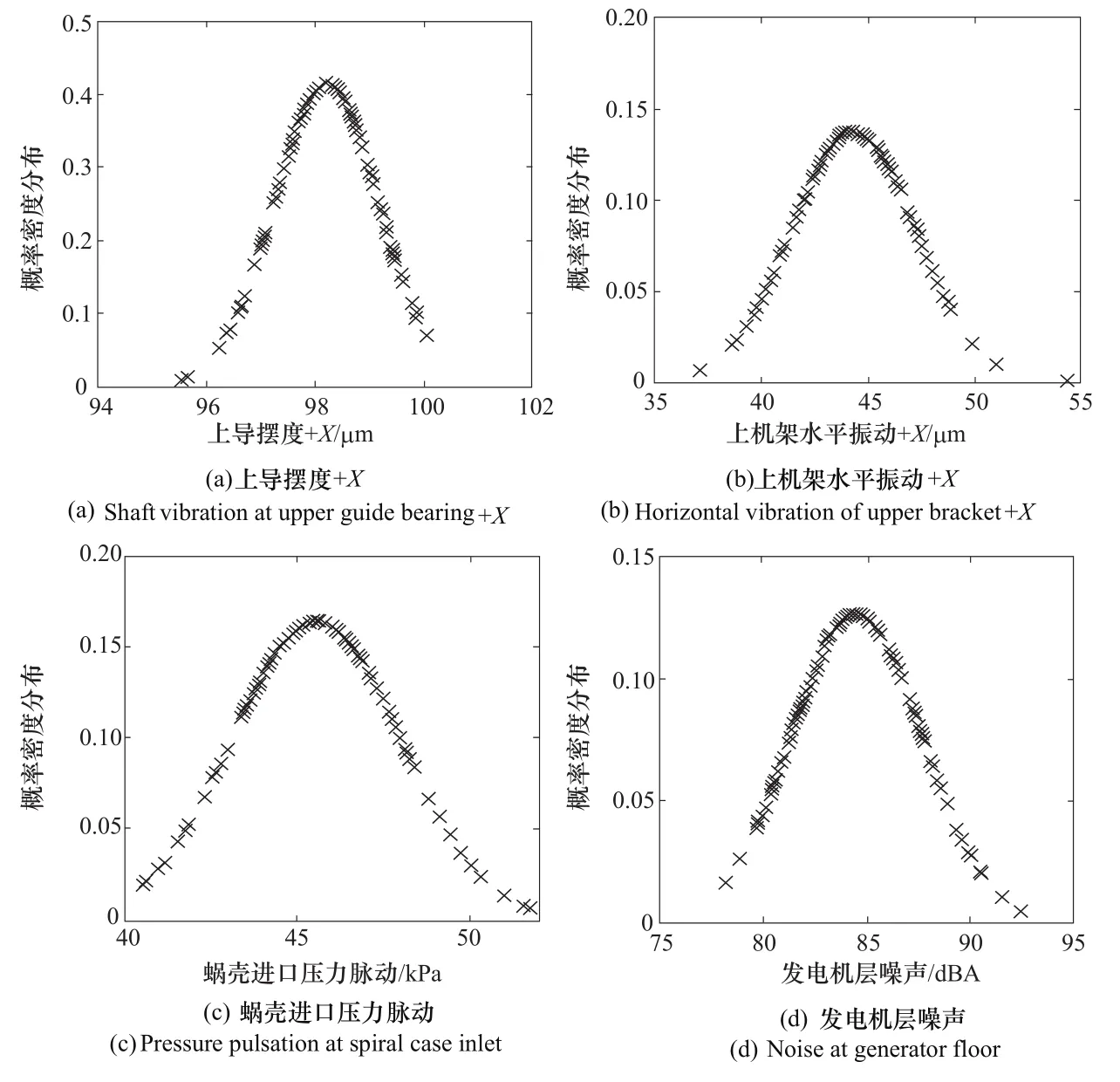
图2 监测参数概率密度分布图Figure 2 Probability density distribution of monitoring parameters
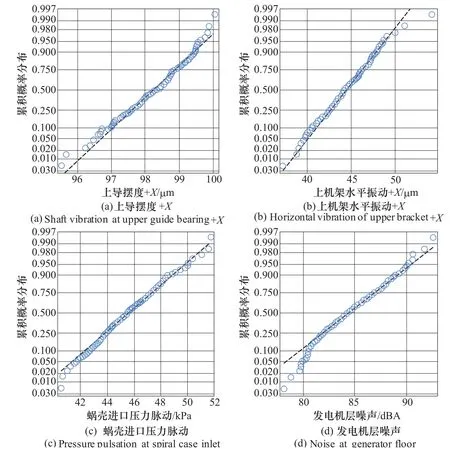
图3 监测参数累积概率分布图Figure 3 Cumulative probability distribution of monitoring parameters
表1中,样本容量n为单次试验的采样次数,试验次数m即样本均值序列的容量,统计值Jbstat均小于临界值CV,检验返回值H均为0,表明4个监测参数的样本均值序列均服从正态分布,验证了检验前的预测。样本均值序列的均值和方差统计同总体的对比如表2所示。
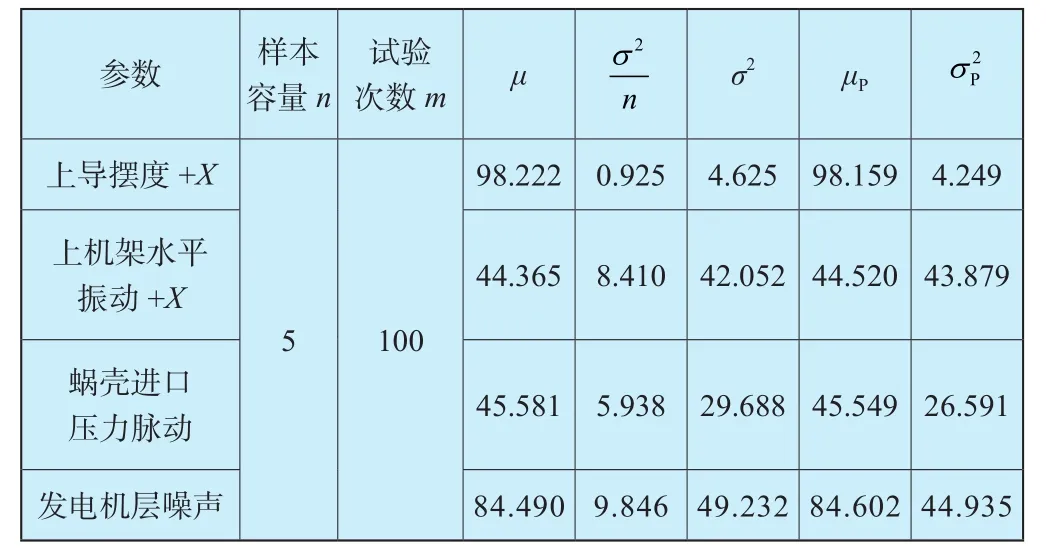
表2 监测参数样本均值与方差估计结果Table 2 Estimation results of sample average and variance of monitoring parameters
从表2可以看出,由样本均值推算出的均值μ和方差σ2同实际总体的均值μP和方差较为接近,可以将经过检验的样本均值序列作为波动预警的数据基础。
2.3 波动预警策略
根据上述检验结果,状态监测参数的样本均值序列服从正态分布,可利用正态分布的知识对其波动阈值进行规定。根据正态分布理论,服从正态分布的监测量在(μ-3σ,μ+3σ)区间波动的概率为99.74%,可根据3σ准则,即判断监测量是否位于该区间来判定该监测量是否超出正常的波动范围,采用该准则可以涵盖绝大部分的正常数据,能够满足工程上的监测需要。
对水电机组状态监测系统,单一阈值的预警依据往往来源于相关国内、外标准的规定,如摆度预警阈值设定来源于GB/T 11348.5—2002《旋转机械转轴径向振动的测量和评定 第5部分:水力发电厂和泵站机组》,振动预警阈值设定来源于GB/T 8564—2003《水轮发电机组安装技术规范》等。当监测参数出现小幅波动,尚未超过预设预警阈值时,系统难以发现和做出及时预警。利用正态分布知识对监测参数进行波动预警,可有效地捕捉这一类异常波动。具体实施时,对任一监测参数,当系统采集到最新的实时监测值时,首先判断其是否超过单一阈值,如超过则马上作出越限预警;计算最新实时监测值与前序相邻若干监测值的均值,若超过根据3σ准则预设的波动区间,则做出波动预警。预警流程图如图4所示。波动预警的模式,可有效监测参数偶然出现的数值波动,若该波动持续不间断地发生,且波动量超出预设区间的程度呈现一定的规律性,则可判断机组存在某种异常,需进行进一步检查。
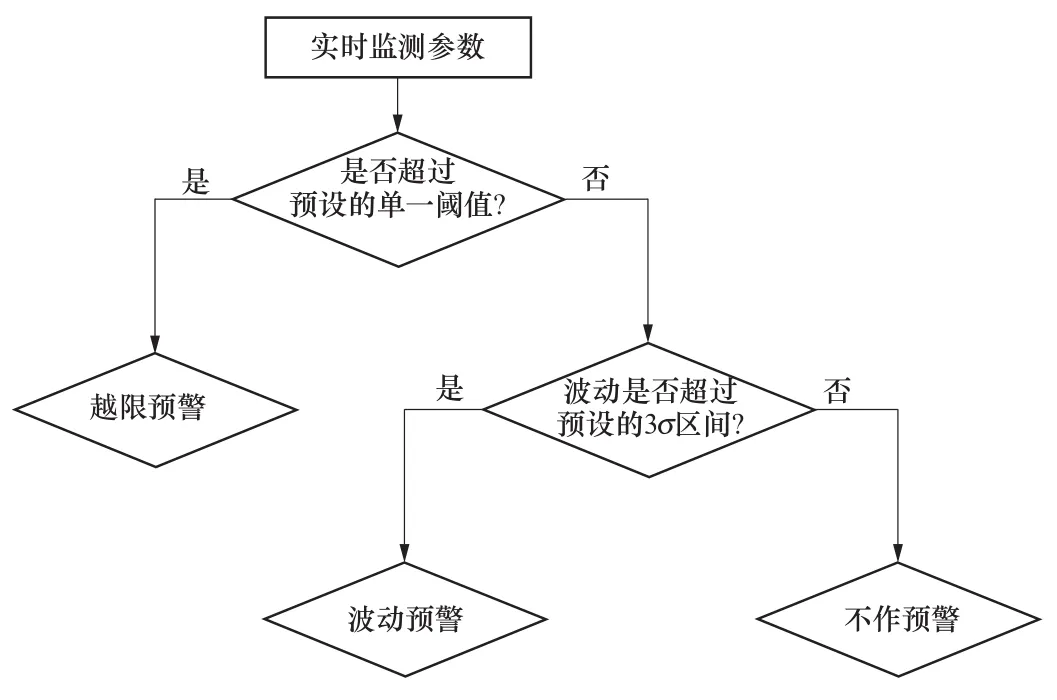
图4 预警策略流程图Figure 4 Flow diagram of alarm procedure
3 结论
本文以水电机组的实际监测数据为研究对象,对其样本均值序列进行了严格的分布检验,结果表明,样本均值序列服从正态分布,验证了中心极限定理的正确性。进而根据正态分布的理论,提出了基于3σ准则的波动预警策略,该预警模式可有效地捕捉状态监测参数的小幅异常波动,对监测参数的波动量做出及时预警,保障机组在发生小幅变化时可被系统及时察觉,有利于机组的长期安全运行。为防止误报、错报发生,本文提出的波动预警策略,仍需得到长期运行的考验,以不断完善,实现科学、全面地监测预警。

