Prediction of Online Judge Practice Passing Rate Based on Knowledge Tracing

HUANG Yongfeng(黄永锋)， CHENG Yanhua(成燕华)

College of Computer Science and Technology, Donghua University, Shanghai 201620, China

Abstract: Programming ability has become one of the most practical basic skills， and it is also the foundation of software development. However, in the daily training experiment, it is difficult for students to find suitable exercises from a large number of topics provided by numerous online judge(OJ) systems. Recommending high passing rate topics with an effective prediction algorithm can effectively solve the problem. Directly applying some common prediction algorithms based on knowledge tracing could bring some problems, such as the lack of the relationship among programming exercises and dimension disaster of input data. In this paper, those problems were analyzed, and a new prediction algorithm was proposed. Additional information, which represented the relationship between exercises, was added in the input data. And the input vector was also compressed to solve the problem of dimension disaster. The experimental results show that deep knowledge tracing (DKT) with side information and compression (SC) model has an area under the curve (AUC) of 0.776 1, which is better than other models based on knowledge tracing and runs faster.

Key words: individualized prediction; knowledge tracing; online judge (OJ); recommending; deep learning

Introduction

As the online judge (OJ) systems have accumulated many exercises so far, it is difficult for students to choose suitable topics[1-2]. Moreover, solving those programming exercises with a certain passing rate can effectively improve learning interest and encourage students to keep practicing[3-5]. Therefore, recommending exercises by predicting the passing rate is our purpose in this study.

There are many algorithms in predicting the passing rate of programming exercises of students in the last years. Thai-Ngheetal.[6]proposed a novel approach using matrix factorization, which predicted the passing rate of unfinished programming exercises based on the previous performance matrix of students. However, the generalization ability of matrix factorization was weak, as it was difficult to integrate more useful features in the learning process. Corbett and Anderson[7]proposed another popular method, called Bayesian knowledge tracing(BKT), which assumes that the student knowledge state was represented as a set of binary variables, where the knowledge was either mastered or not. However, it ignored the relationship among knowledge points because they were trained separately in the model. To establish the connections among knowledge points in training, Kaseretal.[8]studied the hierarchy and relationship among knowledge combinations. Unfortunately, the accuracy of prediction results was still insufficient. Recently, a more accurate model of knowledge tracing had been proposed by Piechetal.[9], called deep knowledge tracing(DKT), which was based on a neural network. It has a better performance than the classic BKT model[10].

The input of the knowledge tracking model mentioned above is all knowledge points, which assumes that the programming exercises under the same knowledge point are equivalent[11-13]. However, the programming exercises often have many differences, even if they have the same knowledge points, such as the difficulty of each exercise[14]. Therefore, replacing the knowledge points with exercises without any processing may lead to certain errors. In our algorithm, we use additional feature information, knowledge points, and programming exercises to establish the connection between the exercises. What’s more, we use linear transformations to compress the input size to save running time and memory.

1 Problem Statement and DKT Overview

1.1 Problem statement

In the OJ system, there areUstudents,Qprogramming exercises, andMknowledge points. We record the learning process for each student asu= {(q1,r1), (q2,r2), …, (qt,rt)}, whereu∈U,qt∈Qandqtrepresents the programming exercise that the studentupracticed at timetandrtrepresents whether the student gets the correct answer of the exercise. Generally, if the student answers programming exerciseqtright,rt=1; otherwise,rt=0. Each programming exercise has no less than one knowledge point, represented by a problem-knowledge point matrixk∈{0, 1}q, m, if problemqcontains knowledge pointm,kq, m=1; otherwise,kq, m=0.

According to the above definition, our task is to train a knowledge tracing model, and predict the probability of getting the correct answer to the programming exercise at timet.

1.2 DKT model

DKT model uses a recurrent neural network (e.g., long short term memory network, LSTM) to predict the passing rate of students in their programming exercises using previous records. The model diagram is shown in Fig. 1.

The input to this model is a time series that consists of knowledge points interaction sequences, given byu= {(s1,r1), (s2,r2), …, (st,rt)}, wherestrepresents the knowledge point of a certain programming exercise.xtis set to be a high-dimensional one-hot encoding of the knowledge point interaction tupleut= {st,rt},xt∈{0, 1}2M, whereMis the number of knowledge points, and the correctness of the programming exercisesrtis extended to a sequence0= (0, 0, …, 0) with the same dimensions of programming exercises embeddingvt. Ifstandrthave separate representation, the performance will be reduced[9]. The entire input is shown as

(1)

where0∈RM,xt∈R2M, ⊕ represents the combination of two vectors. This input could contain information about whether the correctness of answering the exercise influences the student master knowledge points. The forward equations of the DKT model using LSTM are given by

ht∈A(xt),

(2)

yt=σ(Wyhht+by),

(3)

whereArepresents the formula of LSTM,htis the estimated knowledge state of the student at timet, theσis the sigmoid function. The final outputyt∈RMof the DKT model predicts the student’s proficiency over the knowledge points for next time stept+1. Since the assumption of DKT is that the mastery in the knowledge point is equivalent to mastery in any of the exercises containing the point, the lossltfor a specific student is defined as

lt=l (yt[st+1],rt+1)

,

(4)

whereyt[st+1] is the success probability for the skillst.

2 Proposed Model: DKT with Side Information and Compression(DKT-SC)

The proposed model, DKT-SC, is applied to predict the passing rate of finishing each programming exercise rather than for each skill or knowledge point. Therefore, the input to the DKT-SC model is the identity of programming exercises. Compared with DKT model，the DKT-SC model is improved in two aspects, including addition of knowledge point information and compression of input, which are described in sections 2.1 and 2.2.

2.1 Addition of knowledge point information

Some programming exercises are similar, but others do not even contain the same or similar knowledge points. Considering the relationship between programming exercises is a good way to help students find suitable topics. However, the relationship among programming exercises would be ignored if utilizing the identity of exercises only as input. Therefore, additional information needs to be added to the input. Here, we directly appended additional information such as knowledge points to the end of the input in Eq. (1), which is quite simple and effective. In this way, the input contains both programming exercises information and knowledge points information. We useptas the programming exercises embedding. The improvement in the input is given by

(5)

Compared with Eq. (1), Eq. (5) substitutes programming exercises embeddingptfor skill embeddingvt, and appends knowledge pointkqat the end of input.

2.2 Compression of input

The input size is too large to train when the identity of programming exercises are used as input due to numerous exercises provided by the OJ system. If some additional information is contained, the size will become much larger, resulting in a disaster in the training process. Consequently, a linear layer is employed to compress the size of the input. The specific method is given by

yt=wxt+b.

(6)

The dimension size ofwis set to compress the size of input into the specified size. The compressedytis used as the input of the DKT model. After compressing the data, the corresponding running time is shortened, and the memory is saved.

2.3 DKT-SC model

The input to the DKT-SC is the complete sequence of exercise recordu= {(q1,r1), (q2,r2), …, (qt,rt)}, whereqtrepresents the question answered at timetandrt∈{0, 1}.[Also, the additional information and knowledge points are appended to the input and then the input is compressed. Our goal is to predict, at the next time stept+ 1, the probability that the student will answer all theQquestions. DKT-SC has the same formula as DKT, as specified in Eq. (2). Simultaneously, a dropout layer is applied to solve the overfitting problem, and the formula is as follows

yt=σ(Wy·dropout(ht)+by).

(7)

The update lossltfrom Eq. (4) at timetis given by

lt=l (yt[qt+1],rt+1).

(8)

The structure of the whole model is shown in Fig. 2.

3 Experiments

3.1 Datasets and preprocessing

The experimental data are crawled from the codeforces (CF) website using crawler technology. The CF website has many users and programming exercises, and most programming exercises have corresponding knowledge points.

After crawling the data, the data processing is needed. Firstly, the programming exercises without knowledge points are removed which would affect training. Secondly, programming exercises with little user records are removed. These exercises have little contribution to the model, which will seriously delay the training of the model[15]. Finally, the crawled dataset includes 4 070 student users, 6 417 programming exercises, and 37 knowledge points.

In the dataset, if one student submits the same programming exercise repeatedly, it will bring duplicate records. To train the data conveniently, the correctness of the first submission result of one programming exercise is recorded as part of the input information, and the number of student records on the programming exercise as additional information.

3.2 LSTM

In the experiments, the DKT model is implemented based on LSTM. We set the dimension of hidden states in LSTM as 512, the output dimension as 6 417, which is the number of programming exercises. The input dimension in the basic DKT is 12 834, which is twice the number of programming exercises. The input dimension in the model with knowledge points is 12 871, and the input dimension in the model with compression is 512. The number of hidden layers in the LSTM is 1. All the models are trained using the Adam optimizer[16]and adding the clip_grad clipping gradient to mitigate network training termination caused by gradient disappearance or explosion.

3.3 Area under the curve(AUC)

For the performance evaluation, we use the AUC to predict results as a performance metric. Meanwhile, In the experiments, 80% of the dataset is used for training and the rest for testing. Given that several improvements are included in the model, five different methods based on LSTM are compared.

(1) The classic DKT model with input of programming exercises.

(2) The DKT model with input of programming exercises and dropout layer.

(3) The DKT with the side information(DKT-S) model with the addition of knowledge point information and dropout layer.

(4) The DKT with the compression(DKT-C) model with input of programming exercises, compression for the input, and dropout layer.

(5) The DKT-SC model with the addition of knowledge point information, compression for the input and dropout layers.

3.4 Running time of each method

During the experiment, the running time of each method is recorded to evaluate the operational efficiency. The methods are tested with the Tesla T4 GPU. The running time records the seconds that takes to one iterate.

4 Results and Discussion

4.1 Comparison between LSTM and RNN

The AUC of the predicting results of the two network models, namely RNN and LSTM, are shown in Fig. 3. The results indicate that the LSTM model generally performs better than the RNN network model, causing gradient disappearance or gradient explosion[17]. The average length of our data sequence is 960, which means the application of the RNN model can easily come to the problem of gradient disappearance or gradient explosion, and bad results are unavoidable.

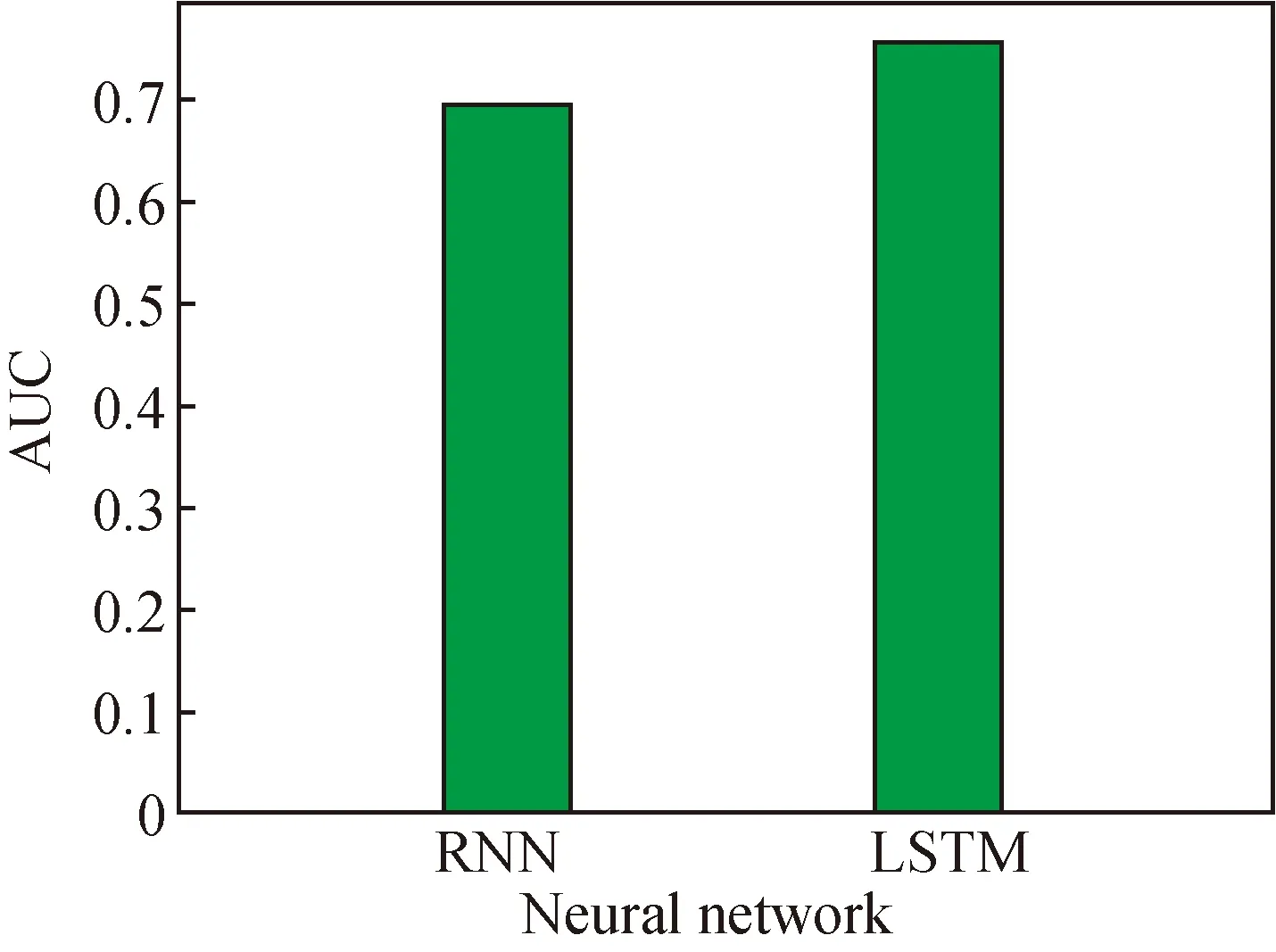
Fig. 3 AUC of two networks

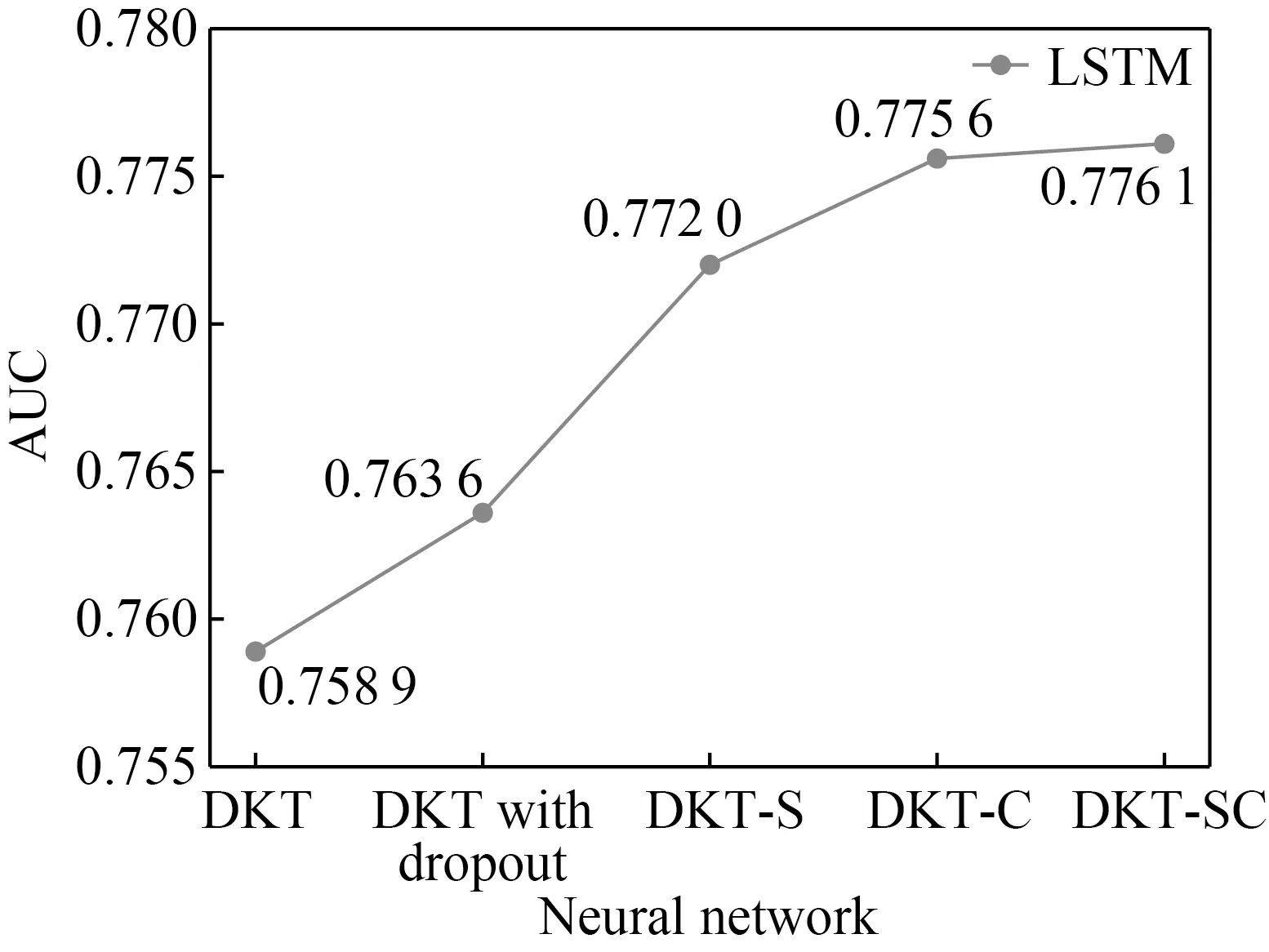
Fig. 4 AUC results of five models

4.2 AUC results

Figure 4 shows the AUC of the five methods. It can be seen that DKT-SC, the model with additional information and input vector compression, has the best results. Since the DKT-S and DKT-C have better results than the DKT, adding additional information and compressing the input vector results are improvements over the classic DKT model. We can find that adding the dropout layer in the network can better improve the performance[18].

4.3 Running time

The running time of each model is recorded in Table 1. It can be seen from Table 1 that the running time of the DKT-C is almost half of the DKT when the input is compressed. Without compressing the input, the running time of the DKT-S comes to 1 123.9 s by adding extra information, which is 24% more than that of the DKT. However, the DKT-SC has a comparable running time to that of the DKT-C. The results in Table 1 indicate that the running time is significantly shortened by compressing the input, which would greatly benefit the future deployment of the model.

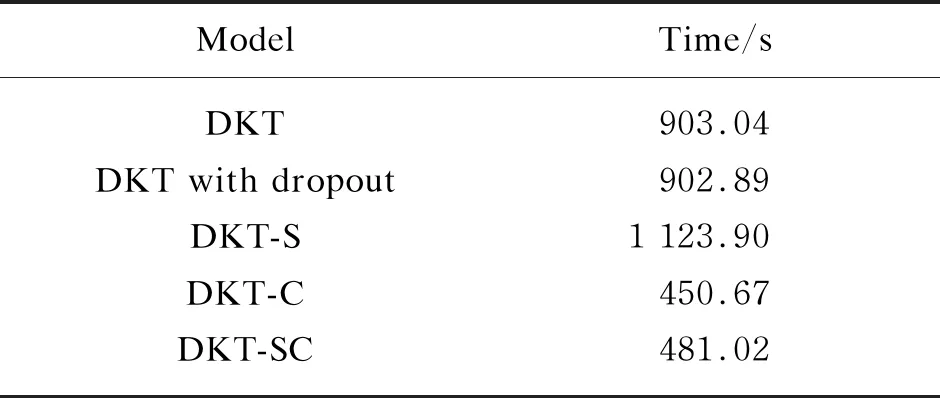
Table 1 Running time of each model

5 Conclusions

In our work, the DKT model is applied to predict the passing rate of students in finishing programming exercises. Two improvements are implemented to reach better performance. The DKT-SC model could achieve 0.776 1 in predicting AUC, which is better than that of DKT model. In addition, the running time of this model is almost half of that of DKT model.

In the future, we would like to introduce other information such as difficulty level to the input and encode the input in different forms. It would be a better choice for us to use graph model or knowledge graph to represent the relationship between exercises.