把握四“度” 搭建“云梯”

倪志敏

摘 要：正比例和反比例，属于“数与代数”领域。本单元教学，笔者认为可以把握好四“度”——高度、角度、牢固度、灵活度，为学生搭建寻求变化数量之间规律的“云梯”。

关键词：正比例和反比例;函数关系;四“度”  “云梯”

正比例和反比例的关系，本质上是函数关系。函数以运动、变化的观点反映事物数量之间的相互联系和内在规律。但是正比例和反比例教学，历来被数学老师们概括为有三难——概念抽象、思维复杂、关系隐晦。在疫情防控期间，学生已通过观看“名师空中课堂”教学视频学习了这部分知识。因此，复学前，笔者以一道题对“正比例和反比例”单元进行了前测摸底。

题目呈现：圆的周长一定，圆的直径和圆周率成比例吗？如果成比例，成什么比例？如果不成比例，为什么？

测后经统计，全班53名同学一致认为圆的直径和圆周率成反比例。因为圆的直径×圆周率=圆的周长（一定）。

如何让“正比例和反比例”单元教学，在复学后的数学课堂能够平稳着地，笔者认为可以把握好四“度”，为学生搭建寻求变化数量之间规律的“云梯”。

一、由薄到厚，定好“云梯”的高度

考虑到学生在疫情防控期间学习效果的差异性，因此复学后的“正比例和反比例”单元教学应既不等同于新课，也不等同于复习。如果说以往的复习重在“融会贯通”，而复学后的本单元教学则首要重在“查漏补缺”，厘清概念，注重概念的“生长点”与“延伸点”，让知识生发“由薄到厚”。通过前测题，笔者认为学生对于正比例和反比例概念的“生长点”——“相关联”理解不到位。成正比例或反比例的两个量必定是相关联的，所以认识正、反比例关系之前，应该先认识相关联的量。

【案例片段】

出示：下题中的两种量是否是相关联的量？为什么？

（1）购买同一种铅笔的数量和总价。

（2）一辆自行车在公路上行驶，行驶的时间和路程如下表：

（3）用60元购买笔记本，购买笔记本的单价和数量。

（4）读一本书，已读页数和剩下页数。

（5）圆的直径和圆周率。

“一种量变化，另一种量也随之变化”这种“关联性”体现在5道题的比较辨析中，让学生深刻理解题5中，圆周率是固定不变的，它不会随着直径的变化而变化。因此，圆的直径和圆周率不是两种相关联的量。既然不是两种相关联的量，那么这两种量既不成正比例，也不成反比例。

二、由末到本，设定“云梯”的角度

为什么要学习正比例和反比例？这应该是我们在教学前首先要厘清的问题。小学生在学习本单元知识之前，接触的基本上是常量数学的内容，是静态的数学知识。而正比例和反比例研究的是变量与变量之间的关系，两种相关联的量虽然都在变化，但又保持着某种不变。学生感受到这种“变”与“不变”的对立统一性，就受到了辩证思想的影响。所以，“变中找不变（规律）”就是正比例和反比例意义教学中的核心。

【案例片段】

教师继续让学生观察，在题1至题4中，一种量变化，另一种量也随之变化。那么题2中，最后一个空，填多少是根本没有办法确定的。因为正比例和反比例中，两种相关联的量在变化中是相互影响、相互制约的。题2中，路程比时间得到速度，如果速度不确定，路程和时间的变化也不确定，所以最后一个空无法填。因此，这两种量既不成正比例，也不成反比例。

师：那么剩下的4题中，哪两种量成正比例？哪两种量成反比例？为什么？

生1：题1中，=单价（一定）。单价是总价和数量的比值，比值一定，总价和数量就成正比例。

生2：题3中，单价×数量=总价（一定）。总价是单价和数量的乘积，乘积一定，单价和数量就成反比例。

师：题4中，已读页数+未读页数=总页数（一定），那么已读页数和未读页数成什么比例？为什么？

抽象正比例和反比例概念，除了需要情境的支撑，更需要我们返璞归真，由末到本，舍弃其非本质属性的部分而抽取其本质属性。教师要让学生认识到数学学习中，我们要学会寻找变化中的不变。两种量成正比例或反比例关系，它们必定按某种确定的关系进行相应变化，而这种关系只能是商一定或积一定。否则，就既不成正比例，也不成反比例。

三、由单到双，强化“云梯”的牢固度

疫情防控期间，“空中课堂”的课虽上得生动有趣，但隔着屏幕，缺少师生之间面对面的交流互动。复学后，考虑到正比例和反比例毕竟学过，而且在现实生活和生产劳动中经常能够遇到，所以在教学之前，笔者让学生以小组为单位，去找一找生活中有哪些成正比例或反比例的量。回归日常生活，通过寻找成正比例和反比例的量，进一步体验正、反比例关系的本质特征。这是数学概念教学经常需要的“具体化”环节。这一环节通过小组合作的形式要求课前完成，既是“空中课堂”学习效果的反馈，也是一次小组内的“集思广益”。

筆者先汇总学生收集的成正比例和反比例的量，写下相关的数量关系式，然后看其中一个数量关系式：单价×数量=总价。

学生反馈：如果总价一定，单价和数量成反比例。如果确定单价，那么数量和总价就成正比例。如果确定数量，总价和单价成正比例。

接着，教师让学生在组内互相说一说，在时间×速度=路程，工作效率×工作时间=工作总量，长×宽=长方形面积，圆柱的底面积×圆柱的高=圆柱的体积……这些数量关系中，其中一个量一定，另外两个量成什么比例关系？

最后，通过讨论交流，学生发现如果总量一定，两个部分量之间满足反比例关系;如果决定总量的任何一个部分量一定，那么总量和另一个部分量就满足正比例的关系规律。

四、由仿到变，改变“云梯”的灵活度

因时间有限，线上课程速度较快，留给学生思考的时间太少，课堂上学生只能听，来不及练。而练习的题型也只能以教材中的习题为主，就题讲题。生活中，木工师傅连接梯子时，往往会在梯子的顶端部位上各上一对“荷叶”，就能让梯子收缩自如。那么，“云梯”的灵活度也需要安装“荷叶”——相应的变式练习。“变”要把概念的本质属性以不同的方式呈现，引发学生从不同的角度去明晰概念的本质属性和非本质属性之间的区别。

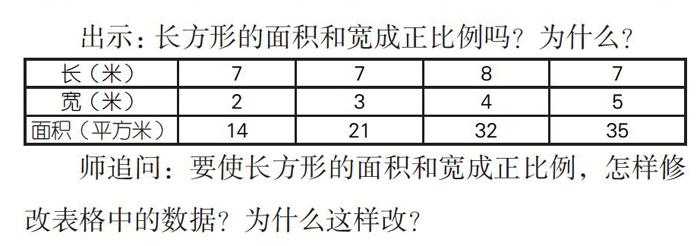
出示：长方形的面积和宽成正比例吗？为什么？

师追问：要使长方形的面积和宽成正比例，怎样修改表格中的数据？为什么这样改？

在正比例和反比例教学中，理解“单值对应”也是一个难点。例题和“试一试”中的题型都是依据表格中的两种量相对应的数值的比值或乘积是否一定，进而判断两种量是否成正比例和反比例。变式练习中的两题，在正、反比例概念的“生长点”的理解运用上避免了机械地重复辨析，让学生逆向思考：乘积或比值一定时，何谓“单值对应”。

总之，疫情复学后的“正比例和反比例”单元教学，笔者认为可以为学生搭建“云梯”，注意把握好四“度”，以寻求变化数量之间的规律。

参考文献

[1]沈重予，王林.小学数学内容分析与教学指导1[M].南京：江苏凤凰教育出版社，2015：117+125.