孤立波漫坝模型试验研究

高红艳 唐英敏 赵立飞

摘 要：水库环境中发生的滑坡涌浪或洪水波传播到大坝附近时会沿着坝体继续爬升，严重时可能会发生漫坝。漫坝水流对下游所造成的危害往往是毁灭性的。为了研究冲击波漫坝时的水力特征，在试验水槽中用孤立波来模拟涌浪漫坝过程。试验中发现孤立波最大漫坝高度发生在坝顶紧靠迎水坡处，且各漫坝指标与静水深度、相对波高、坝前角度、坝顶宽度等控制参数有关。通过对无量纲参数的多元回归分析，建立了漫坝体积、最大漫坝高度和漫坝持续时间的经验计算公式，揭示了孤立波漫坝水力特性与各控制参数间的关系，可为大坝设计及水库漫坝险情应急处理提供参考。

关键词：孤立波;漫坝;模型试验;无量纲分析

中图分类号：TV135.1 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.08.009

引用格式：高红艳，唐英敏，赵立飞.孤立波漫坝模型试验研究[J].人民黄河，2021，43（8）：48-51.

Abstract：Landslide surge occurred in reservoir wasting into the dam generates so-called impulse waves. These waves run up onto shores and may overtop dams which often causes devastating damage to the downstream of the dam. This research dealt with solitary waves to model the overtopping process in a two-dimensional laboratory-scale test setup for studying the hydraulic characteristics of dam overtopping. It was found that the maximum wave overtopping depth locates at the dam crest. The indexes of wave overtopping were related to the governing parameters of still-water depth， relative wave amplitude， dam front face angle and dam crest width. The predictive equations for overtopping volume， maximum overtopping depth and wave overtopping duration were derived in this study by using a multi-variable regression analysis of the dimensionless parameters， which revealed the relationship between hydraulic characteristics and control parameters. This study provided a theoretical basis for dam design and emergency treatment for dam overtopping.

Key words： solitary wave; dam overtopping; model test; dimensionless analysis

高山峽谷水库地质条件复杂，大中型滑坡分布广泛，高速运动的山体滑坡入水后诱发的冲击波会迅速向远处传播。当滑坡发生点距下游水利枢纽较近时，所产生的冲击波无法得到充分衰减，在到达坝前水域时依然具有较大的立波高度并携带巨大能量，导致离岸波沿着坝身继续向上爬动，严重时甚至发生漫坝，对下游居民生命财产及沿岸基础设施造成巨大损失。其中最著名也是最惨痛的案例是发生在意大利瓦伊昂（Vajont）水库的滑坡涌浪事件[1-2]。对于土石坝来说，冲击波或洪水漫溢还会对大坝结构安全造成严重威胁，甚至有发生溃坝的危险[3]。

目前有关水库漫坝的研究仅限于洪水漫坝概率及漫坝风险方面，无法获得洪水溢流波的物理参数及相关特性。李平等[4]通过构建洪水作用下双库连溃的贝叶斯网络模型，分析了四川大渡河上两相邻梯级水库漫坝概率及连溃风险;陈伏龙等[5]采用Pettitt非参数检验法和Mann-Kendall非参数趋势检验法分析肯斯瓦特水库入库年最大洪峰流量序列的非一致性，并通过基于直角梯形模糊数的风险分析法，给出过去、现状两种条件下的水库漫坝模糊风险率。虽然在海岸工程中海防结构的波浪漫溢方面已研究多年并制定了相关规范[6]，但其主要研究的是风浪越顶，其产生机理并不适用于水库冲击波漫坝。因此，需要针对水库环境下滑坡冲击波（或洪水波）的漫坝过程所涉及的水力特征参数进行研究。Mohammed[7]曾通过物理模型试验发现初始滑坡涌浪具有许多类似于孤立波的特征，Superchi[8]在其建立的瓦伊昂滑坡研究模型中也证实了这一点，因此用孤立波来模拟滑坡冲击波的漫坝过程是合理的。笔者通过水槽模型试验，研究了孤立波漫坝过程，并建立了孤立波漫坝水力特征参数的经验计算公式。

1 试验设置

试验在一个长12 m、宽0.5 m的矩形玻璃水槽中进行，模拟了不同坝前角度和坝顶宽度下的孤立波漫坝过程，并通过一台高速摄像机进行记录。模型试验布置见图1。坝体模型由有机玻璃材料制成，孤立波的产生则是采用一台气动活塞式波浪发生器，其造波原理见参考文献[9]。试验研究的变量包括孤立波漫坝体积V、最大漫坝高度d0（x=0处的最大水深）以及漫坝持续时间t0，其中漫坝水体由图1中的蓄水池进行收集。图2显示了孤立波漫坝过程中的相关参数，其中：a为孤波波高，h为水深，w为坝高，bK为坝顶宽度，β为大坝迎水坡角度，孤立波波速c=[g（h+a）]1/2，坝顶到水面的垂直高度f=w-h。表1列出了试验中模型相关参数的取值范围，其中相对波高ε=a/h。在不同水深条件下所产生的相对波高工况组合见表2。考虑到模型尺度效应[10]，将d0<0.05 m时的试验结果忽略。

2 漫坝指标计算公式

对水库涌浪灾害风险评估来说，孤立波漫坝所涉及的主要评估指标包括漫坝体积V、最大漫坝高度d0以及漫坝持续时间t0。试验中相关影响参数包括水深h、波高a、坝顶宽度bK、坝高w和大坝迎水坡角度β。

2.1 漫坝体积

漫坝体积是指孤立波漫坝后在坝下游溢出的水体体积，是研究漫坝后坝下游洪水灾害的重要参数。试验中通过坝后蓄水池收集的水体体积来估算孤立波漫坝体积。图3为h=0.25 m、β=20°时无量纲漫坝体积V/（bh2）随相对波高ε的变化规律。由图3可知，相对波高对漫坝体积的影响十分强烈，且漫坝体积随相对波高的增大而增大;此外，相同条件下坝顶宽度越小，坝面对冲击波的阻力作用就越小，孤立波漫坝体积就越大。当β=45°和90°时，也有相似的变化规律。除了相对波高外，波峰与坝顶间的垂直高度aw（即最大水面超高）也是影响漫坝体积的一个重要因素。通过试验可知，漫坝体积随aw的增大而增大。虽然水深大小与漫坝体积之间并无直接联系，但在波高和坝高一定的情况下，水深增加可使得aw值增大，从而间接对漫坝体积造成影响。通过以上分析，孤立波漫坝体积可用以下无量纲函数表示：

通过对无量纲函数的多元回归分析，得到孤立波漫坝体积的经验公式：

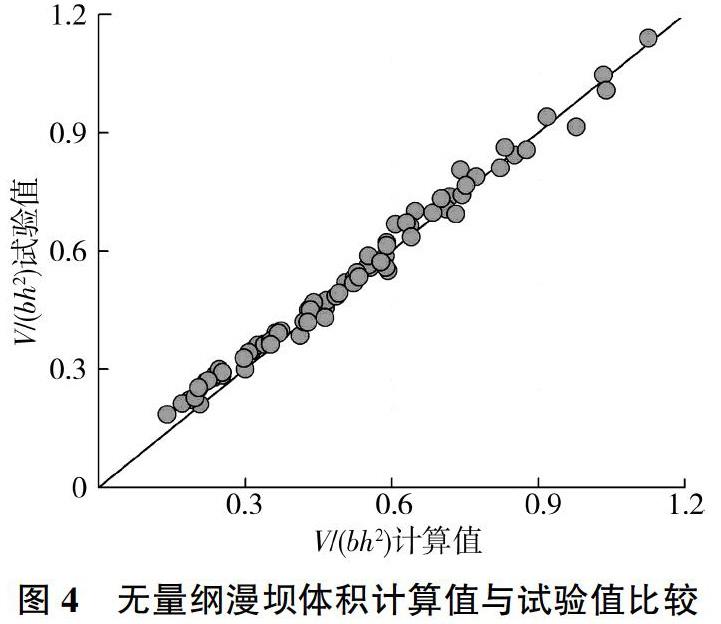
图4为通过式（2）计算的无量纲漫坝体积与试验测量值间的关系，复相关系数R2=0.97。由此可见，式（2）的相关性较好。以上结果从另一方面也反映出：在水库蓄水期，坝前水位较高，则相对水深与相对水面超高较大，当发生滑坡冲击浪时，会产生更大的漫坝体积;此外，孤立波漫坝体积随着坝前迎水坡角度的减小而增大，说明坡度越小，波浪爬坡能力越强。

2.2 最大漫坝高度

除了漫坝体积V外，最大漫坝高度d0也是漫坝风险评估的重要指标，其决定了冲击波漫坝后在坝下游形成洪峰的立波高度及能量大小。试验中发现，孤立波漫坝时的最大漫坝高度发生在坝顶紧靠迎水坡处，即图2中x=0处。图5列出了不同坝前角度的孤立波漫坝过程，结果验证了孤立波最大漫坝高度与坝前迎水坡角度β及坝顶宽度bK无关。

图6为h=0.3 m时无量纲最大漫坝高度d0/w随相对波高ε的变化规律，可以看出，无量纲最大漫坝高度与相对波高之间有较好的线性关系，且随着相对波高的增大而增大;此外，β也对漫坝高度产生影响，当坝前迎水坡角度增大，迎水坝面对波的阻力作用增强，导致坝前水体产生挤压，漫坝高度增加，同时消能效果也显著增强。

参照式（1），通过无量纲分析与多元回归分析，得到孤立波最大漫坝高度的经验公式：

式中：d0/w为无量纲最大漫坝高度。

图7为通过式（3）计算的无量纲最大漫坝高度与试验测量结果间的关系，复相关系数R2=0.93，相关性较好。由式（3）可以看出，孤立波漫坝高度随相对波高、相对水深的增大而增大;与漫坝体积不同，孤立波漫坝高度随着坝前迎水坡角度的减小而减小，其原因是迎水坡角度越大，波浪上坝时速度越慢，壅水作用越明显，导致漫坝高度增加。

2.3 漫坝持续时间

漫坝持续时间可用来分析冲击波漫坝后在坝下游形成的洪水流量过程。试验中通过在水槽一侧布置的高速摄像机跟踪记录孤立波漫坝过程，进而得到漫坝持续时间。Müller[11]曾研究坝顶到水面垂直高度f=0情况下的涌浪漫坝持续时间t0，并得到以下计算公式：

式中：T为冲击波在到达坝前时的周期;h为坝前水深;g为重力加速度。

由于f=0属于极端情况，因此式（4）不具有普适性。通过本试验结果，对f>0情况下的孤立波漫坝持续时间进行分析，并对其进行无量纲化處理，得到无量纲漫坝时间w/g/t0。图8为h=0.25 m时无量纲漫坝时间随相对波高ε的变化规律，可以看出漫坝持续时间t0随相对波高的增大而减小，并随着大坝迎水坡角度的增大而增大。2.1节中曾提到水深增加可使得aw值增大，从而间接增大了漫坝体积，由此产生了更长的漫坝时间。而大坝迎水坡角度的增大可对来流产生更大的阻力作用，使得孤立波坝前波速减慢，导致漫坝时间增加。因此，可以基本确定漫坝持续时间与相对波高ε、相对水深h/w以及坝前迎水坡角段β有关，对参数进行无量纲处理后得到：

通过试验数据对式（5）进行多元回归分析，得到f>0时孤立波漫坝持续时间t0的经验公式：

图9为通过式（6）计算的无量纲漫坝持续时间与试验测量结果间的关系，复相关系数R2=0.98，相关性较好。由式（6）可以反映出，孤立波漫坝持续时间随相对水深的增大而减小，说明在水库蓄水期，坝前水位较高时，冲击波漫坝速度更快，对坝面持续作用时间较短;而在水库枯水期，坝前水位较低时，冲击波漫坝持续时间较长，很可能会对土石坝坝体结构稳定造成更不利影响。此外，孤立波漫坝持续时间随着坝前迎水坡角度的增大而增大，进一步证明了坝体坡度越小，波浪爬坡能力越强。

3 结 语

通过物理模型试验研究了孤立波漫坝过程，试验控制参数包括水深、坝高、大坝迎水坡角度、坝顶宽度以及孤立波波高。试验分析了孤立波漫坝时3个主要的水力特征参数，即漫坝体积、最大漫坝高度和漫坝持续时间。通过无量纲分析与多元回归分析，得到孤立波漫坝体积、最大漫坝高度和漫坝持续时间的经验计算公式。从与试验结果的比较来看，经验公式的相关性较好，可为大坝结构设计以及冲击波漫坝风险评估提供一定的参考。受试验条件限制，并未研究孤立波漫坝后在坝下游形成的洪水波过程;此外，本试验结果是由二维模型得到的，现实中冲击波漫坝时沿坝顶长度方向上的漫坝过程是否满足二维单宽情况，还有待进一步验证。

参考文献：

[1] ZHAO T， UTILI S， CROSTA G B. Rockslide and Impulse Wave Modelling in the Vajont Reservoir by DEM-CFD Analyses[J]. Rock Mechanics and Rock Engineering， 2016， 49（6）： 2437-2456.

[2] KIERSCH G A， ASCE F. Vaiont Reservoir Disaster[J]. Civil Engineering， 1964（3）： 32-39.

[3] 陈玺，孙平，李守义，等.考虑地震与溃坝洪水共同作用的土石坝坝坡稳定分析方法[J].水利学报，2017，48（12）：1499-1505.

[4] 李平，黄跃飞，李兵.基于贝叶斯网络的梯级水库连溃风险[J].水科学进展，2018，29（5）：73-80.

[5] 陈伏龙，张鑫厚，冯平，等.基于非一致融雪洪水的水库漫坝模糊风险分析[J].水力发电学报，2018，37（12）：22-32.

[6] HUGHES S. Advanced Series on Ocean Engineering 7： Physical Models and Laboratory Techniques in Coastal Engineering[M].Singapore：World Scientific Publishing， 1993：256-268.

[7] MOHAMMED F. Physical Modeling of Tsunamis Generated by Three-Dimensional Deformable Granular Landslides[D]. Atlanta： Georgia Institute of Technology， 2010：132-145.

[8] SUPERCHI L. The Vajont Rockslide： New Techniquesand Traditional Methods to Re-Evaluate the Catastrophic Event[D]. Veneto： Padova University， 2012：97-106.

[9] GORING D G. Tsunamis： The Propagationof Long Waves onto a Shelf[D].Pasadena：California Institute of Technology， 1978：36-49.

[10] FUCHS H， HAGER W H. Solitary Impulse Wave Transformationto Overland Flow[J]. Journal of Waterway Port Coastal and Ocean Engineering， 2015， 141（5）： 04015004.

[11] MLLER D. Run-up and Run-over of Impulse Waves at Dams[R].Switzerland： ETH Zurich， 1995：77-85.

【責任编辑 许立新】