基于地理加权回归模型的博斯腾湖湖滨绿洲土壤盐分离子含量高光谱估算①

赵 慧，李新国*，靳万贵，牛芳鹏，麦麦提吐尔逊·艾则孜

基于地理加权回归模型的博斯腾湖湖滨绿洲土壤盐分离子含量高光谱估算①

赵 慧1, 2，李新国1, 2*，靳万贵1, 2，牛芳鹏1, 2，麦麦提吐尔逊·艾则孜1, 2

(1 新疆师范大学地理科学与旅游学院，乌鲁木齐 830054；2 新疆干旱区湖泊环境与资源实验室，乌鲁木齐 830054)

以博斯腾湖湖滨绿洲为研究区，分析HCO– 3、Cl–、SO2– 4、Ca2+、Mg2+、Na++K+等主要土壤盐分离子含量与土壤高光谱反射率的分数阶微分光谱变换与RSI、DSI、NDSI等二维土壤指数的相关性优选特征波段，构建基于地理加权回归模型的土壤盐分离子含量估算模型。研究结果表明：Na++K+的微分变换特征波段集中在468 ～ 724 nm与1 182 ～ 1 539 nm，二维土壤指数的特征波段集中在1 742 ～ 2 395 nm，基于RSI的特征波段优选下地理加权回归模型对Na++K+含量的估算效果较好，建模集2= 0.94，RMSE = 0.22，验证集2= 0.74，RMSE = 0.19；SO2– 4含量在1.2阶优选的位于469 ～ 636 nm波段估算效果较佳，建模集2= 0.91，RMSE = 0.02，验证集2= 0.75，RMSE = 0.33；Ca2+、Mg2+优选的特征波段主要集中在912 ～ 2 340 nm的近红外波段；Cl–含量在1阶的近红外波段建模效果较好，建模集2= 0.74，RMSE = 0.03，验证集2= 0.93，RMSE = 0.11；含量相对较高的Na++K+、SO2– 4、Cl–的地理加权回归模型精度高于含量较低的Ca2+、Mg2+。

土壤盐分离子；分数阶微分；光谱矩阵系数图；地理加权回归模型；湖滨绿洲

土壤中不同盐分离子对作物的毒害不同，土壤盐分离子的分异对作物的危害性往往高于总盐的危害[1-2]。传统土壤盐分离子的测定需要耗费时间，且步骤繁琐，而高光谱遥感技术可以充分挖掘光谱信息和构建高精度的模型[3]。土壤盐分离子的含量和特征在一定程度上决定了盐渍化的性状和程度，将土壤盐分离子和高光谱数据综合考虑，筛选其特征波段，可以明确研究区土壤盐分离子的特征光谱，提高土壤盐分离子的估算精度和实用性[4-5]。郭鹏等[6]采用混合波段和筛选波段的方法以提高土壤盐分离子估算模型的精度；张俊华等[7]基于0 ～ 5 cm和0 ～ 20 cm对比分析土壤盐分离子在不同土层的估算模型。针对分数阶微分预处理高光谱数据的方法中，有采用Savitzky-Golay加一阶微分变换和以不同间隔的分数阶微分变换等不同方式[8-9]。亚森江·喀哈尔等[10]认为利用分数阶微分优化光谱指数对土壤电导率的特征波段敏感程度更强。高光谱数据常用的模型估算方法有神经网络模型、偏最小二乘、支持向量机等[11-13]。袁玉芸等[14]利用地理加权回归模型(GWR)分析于田绿洲土壤表层盐分高光谱数据估算精度优于OLS模型。GWR能够考虑到空间异质性，将采样点的坐标代入不同的系数，就能进行空间坐标分析，通过建立空间尺度上每个点的局部回归方程，能有效揭示土壤属性空间变异特征关系[15]。空间关系约束的高光谱土壤盐分离子估算方面研究鲜有报道。针对干旱区湖滨绿洲土壤盐分离子的空间异质性，开展以博斯腾湖湖滨绿洲为研究区，分析土壤盐分离子与相关光谱参量间的关系，构建地理加权回归模型，将每个样本点加入空间坐标估算土壤盐分离子含量。

1 材料与方法

1.1 研究区概况

博斯腾湖湖滨绿洲行政区划隶属于新疆博湖县，位于新疆焉耆盆地东南部，地理位置介于86°15′ ～ 86°55′E，41°45′ ～ 42°10′N(图1)。其是典型的人工绿洲和自然绿洲混合的山前湖泊绿洲，面积为1 360 km2。湖滨绿洲受到博斯腾湖水域的调节，年平均气温8.2 ～ 11.5 ℃，无霜期175.8 ～ 211.3 d，年蒸发量1 880.0 ～ 2 785.8 mm，年降水量47.7 ～ 68.1 mm，蒸降比高达40:1。研究区内土壤类型主要有沼泽地、草甸土、灌耕潮土、风沙土、盐土、棕漠土等，地下水埋深1.0 ～ 2.5 m，矿化度为0.1 ～ 10 g/L[16-17]。研究区土地利用/覆盖类型主要为耕地与未利用地，土壤盐分以氯化钾钠盐和硫酸钾钠盐为主，主要土壤盐分离子有HCO– 3、Cl–、SO2– 4、Ca2+、Mg2+、Na++K+。

1.2 土壤样品采集及测定

根据研究区土壤类型的现状，结合研究区的土壤盐分状况，采用GPS定位技术，使采样点尽可能遍及研究区范围内的主要土地利用类型，考虑采样点的水文地貌条件、植被覆盖类型以及土壤盐渍化程度等因素，选取34个样点进行土壤采集(图1)，每个样点3次重复。采样时间为2019年7月8日，采用分层随机取样的方法，每个样本点范围分0 ～ 10、10 ～ 20 cm采样土层进行，共计68份。土壤光谱测定采用ASD FieldSpec3便携式地物光谱仪，波段范围为350 ～ 2 500 nm，野外测量需要选择晴朗无风的天气，采集光谱前对光谱仪白板校正，且校正间隔控制在5 min[18]，每个土壤样品重复测量20条光谱曲线，取其平均值作为此样本的光谱数据。对均值处理后的光谱曲线去除水分吸收带波段，对去除干扰波段的光谱曲线用Savitzky-Golay滤波方法进行平滑处理。

1.3 数据处理与研究方法

1.3.1 分数阶微分 分数阶微分是将整数阶微分的阶数扩展至任意阶。目前，在众多的分数阶微分定义形式中[19-20]，Grünwald-Letnikov(G-L)定义的分数阶微分较为常用，主要是应用一元函数差分来实现，表达式为：

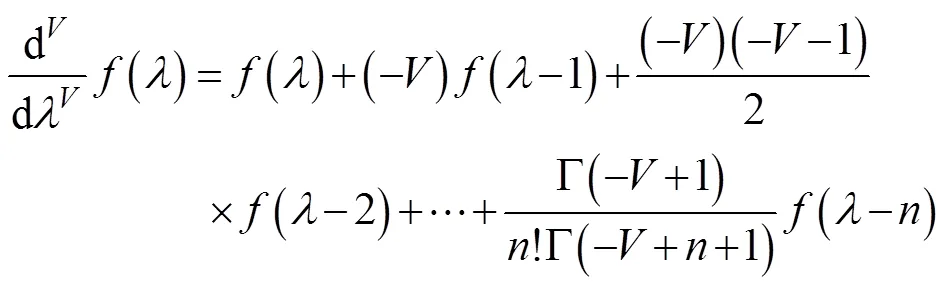
1.3.2 光谱指数 根据研究区土壤盐分离子状况，结合前人的研究结果，光谱指数采用比值盐分指数(ratio salt indices，RSI)、差值光谱指数(difference spectral indices，DSI)和归一化光谱指数(normalized difference spectral indices，NDSI)[21]。根据全光谱的第波段和第波段的所有组合计算二维相关系数，绘制形成光谱系数矩阵图。光谱指数计算公式：

RSI=R/R(2)

DSI=R–(3)

NDSI=(R–R)/(R+R) (4)

式中：R和R是土壤盐分离子在第波段和第波段的土壤光谱反射率。

1.3.3 地理加权回归 Fotheringham等[22]提出地理加权回归模型(geographically weighted regression，GWR)能够将空间坐标代入到回归参数中，采用的是局部光滑思想，这样能使局部加权的最小二乘法进行样点的估测，其中权重是回归点所在位置到其他观测点的位置之间距离的函数。该模型表达式[23]为：

式中：y为样点的因变量；0为回归常数项；(u,v)为第个采样点的坐标(如经纬度)；β(u,v)是个采样点上的第个回归参数，是地理位置的函数；ε为误差项；x为第个样点上的个变量的观测值。采用带宽优化方法中易于与经典的线性回归模型进行比较的AIC信息准则，表达式为：

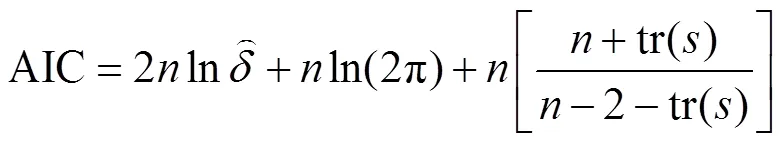
2 结果

2.1 主要土壤盐分离子含量描述性统计

由表1可知，主要土壤盐分离子为HCO– 3、Cl–、SO2– 4、Ca2+、Mg2+、Na++K+。从均值看，研究区土壤的SO2– 4、Na++K+含量最高，分别为1.58和1.59 g/kg；阴离子中Cl–次之；HCO– 3含量最少，为0.11 g/kg。Ca2+、Mg2+含量分别占阳离子的10.64% 和10.95%，Cl–占阴离子的15.06%。结合前人的研究结果，在后续建模中以3︰1比例选取建模集与验证集[25]。

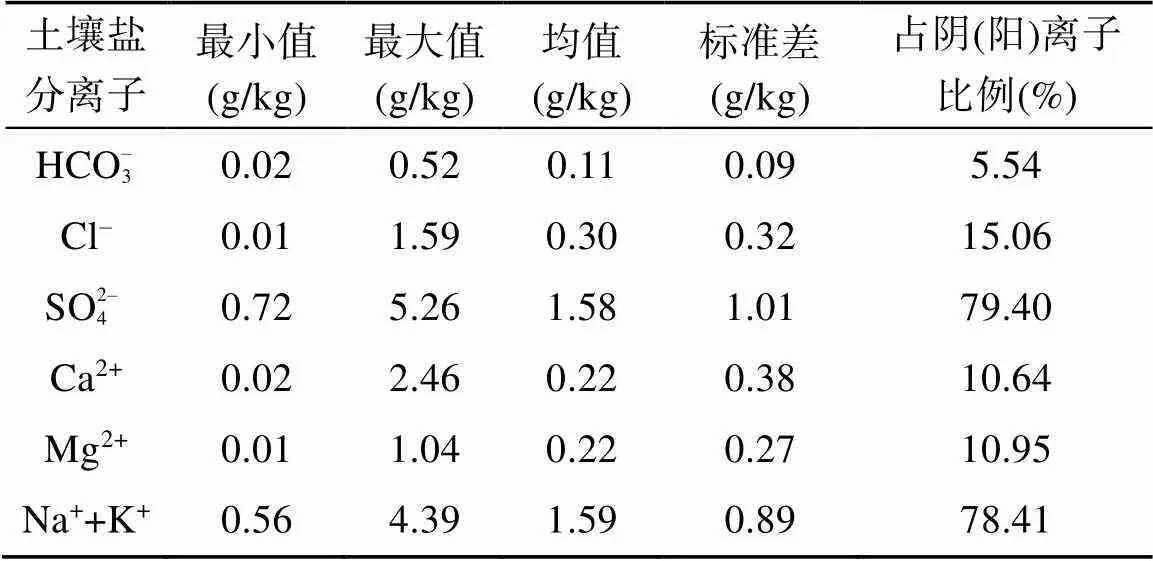
表1 主要土壤盐分离子的描述性统计特征

2.2 一维光谱相关性特征波段选择

由图2可知，对原始光谱反射率以0.2为间隔，在0 ～ 2阶进行微分处理，将分数阶微分变换下的光谱反射率与HCO– 3、SO2– 4、Ca2+、Mg2+、Na++K+、Cl–进行相关性分析，筛选出通过极显著性检验且相关性较高的阶数进行分析。1.6阶和2阶与HCO– 3的相关性较小，通过极显著性检验的波段较少；1阶与Cl–相关性在分数阶微分变化下最优，最大相关系数绝对值为0.57；SO2– 4、Ca2+、Mg2+、Na++K+、Cl–的较大相关系数集中在正相关。波段筛选原则为：在样本数为68，通过显著性检验，即选取相关系数大于0.315的最优4条波段。

由表2可知，对优选出的土壤盐分离子建模所需要的特征波段进行分析，HCO– 3的特征波段主要集中在419 ～ 490 nm可见光紫、蓝光波段；Na++K+的特征波段主要集中在468 ～ 874 nm、1 182 ～ 1 539 nm可见光绿、黄、橙、红光及近红外波段；Cl–的特征波段主要集中在1 253 ～ 2 360 nm近红外波段；SO2– 4的特征波段主要集中在468 ～ 830 nm可见光绿、黄、橙、红光波段，与近红外波段也有一定相关性；Ca2+的特征波段主要集中在1 080 ～ 2 316 nm近红外波段，Mg2+的特征波段主要集中在912 ～ 2 175 nm近红外波段。1 ～ 2阶的光谱反射率与土壤盐分离子的相关性较高，达到显著水平，从而筛选出较优的特征波段。分数阶微分变换下的光谱数据更能深度挖掘光谱中的潜在信息。

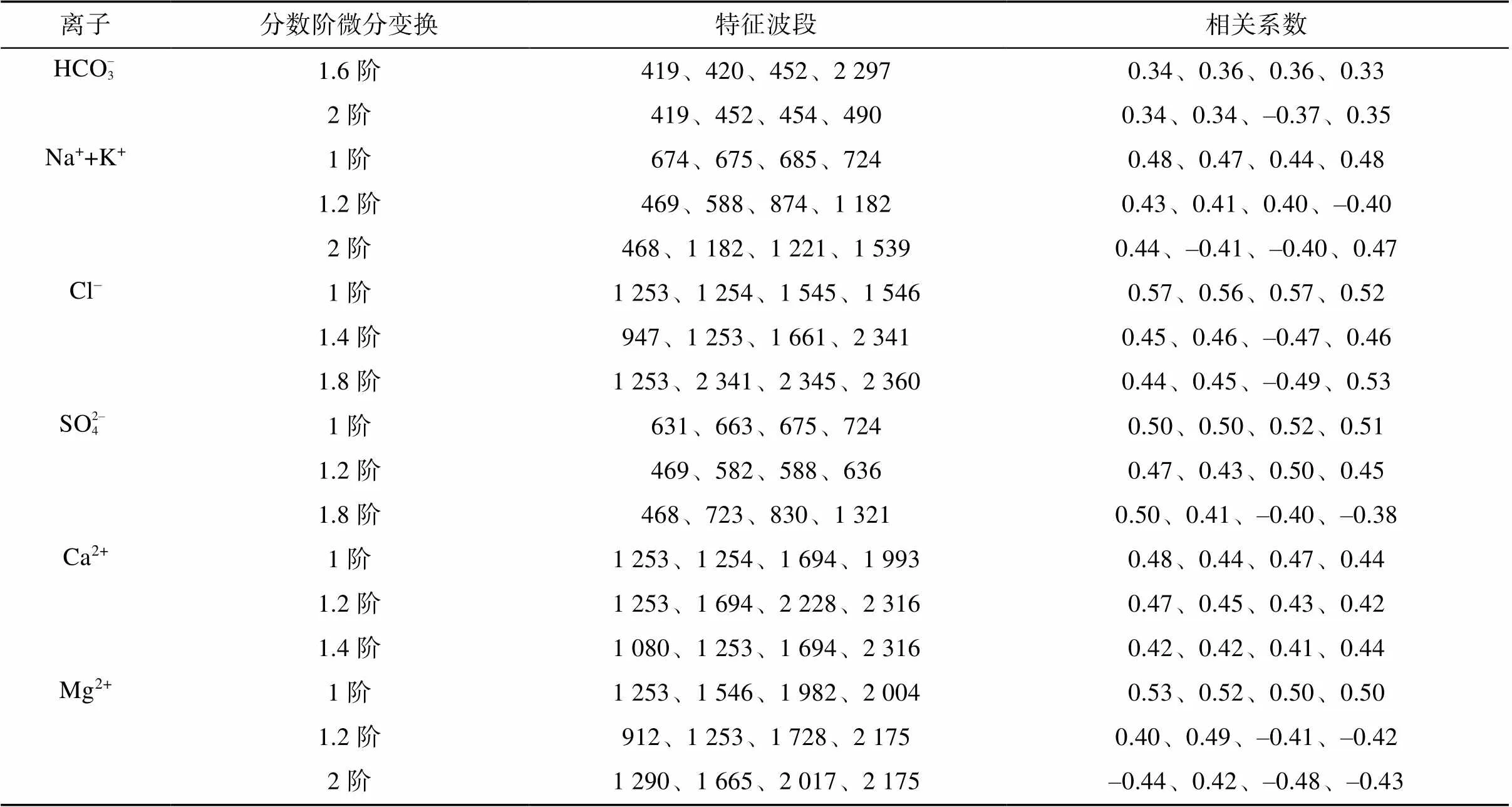
表2 主要土壤盐分离子建模波段及分数阶微分光谱变换形式

2.3 二维土壤指数特征波段选择

土壤盐分离子含量和光谱指数之间的相关性，能够利用二维光谱矩阵系数图进行可视化表达。通过建立HCO– 3、SO2– 4、Ca2+、Mg2+、Na++K+、Cl–分别与原光谱反射率的RSI、DSI、NDSI光谱矩阵系数图，从中选取相关性较高的光谱矩阵图进行分析，如图3可知：同种离子在RSI、DSI、NDSI的光谱指数下二维光谱矩阵系数图具有相似性。其中Cl–的相关性整体大于其他离子，特征波段主要集中在1 461 ～ 1 597 nm和1 710 ～ 1 749 nm，主要位于近红外波段；Mg2+在RSI和DSI的相关性与Cl–的光谱矩阵图相似，但相关系数值比Cl–低；HCO– 3特征波段主要集中在1 550～ 1 760 nm；Na++K+特征波段主要集中在1 742 ～ 2 395 nm；SO2– 4、Ca2+、Mg2+的特征波段主要集中在1 977 ～ 2 340 nm的近红外波段，其中SO2– 4的特征波段还集中在600 ～ 700 nm的可见光红光波段。

优选出的特征波段，用于构建模型的二维土壤指数见表3，由于Mg2+、Ca2+在RSI、NDSI光谱指数下筛选的特征波段相同，分别为(1 989, 2 066)、(2 005, 1 982)，为避免冗余，选择RSI建模。

2.4 地理加权回归模型分析

一维相关优选特征波段和二维相关优选特征波段与土壤盐分离子都具有较高的相关性，为寻找较优的估算模型，分别以HCO– 3、SO2– 4、Ca2+、Mg2+、Na++K+、Cl–为因变量，优选的特征波段分别为自变量，构建地理加权回归模型。由表4可知，由于一维相关和二维相关的RMSE相差较大，因此从一维和二维相关中各筛选出一个较优的建模集，再根据验证集的较优模型确定土壤盐分离子的最优模型。Cl–估算模型中，1阶的2= 0.74最大，RMSE = 0.03最小；DSI的2= 0.82最大，RMSE = 0.11最小，均为建模集较优模型。SO2– 4估算模型中，1.2阶的2= 0.91最大，RMSE = 0.02最小；DSI的2= 0.89最大，RMSE = 0.36最小，均为建模集较优模型。Na++K+估算模型中，1.2阶和2阶的2= 0.74最大，RMSE = 0.01最小；RSI的2= 0.94最大，RMSE = 0.22最小，均为建模集较优模型。HCO– 3估算模型中，2阶的2= 0.23最大，RMSE = 0.01最小；NDSI的2= 0.17最大，RMSE = 0.09最小，均为建模集较优模型。Ca2+估算模型中，1阶的2= 0.75最大，RMSE = 0.03最小；DSI的2= 0.74最大，RMSE = 0.18最小，均为建模集较优模型。Mg2+估算模型中，1.2阶的2= 0.69最大，RMSE = 0.01最小；RSI的2= 0.83最大，RMSE = 0.10最小，均为建模集较优模型。

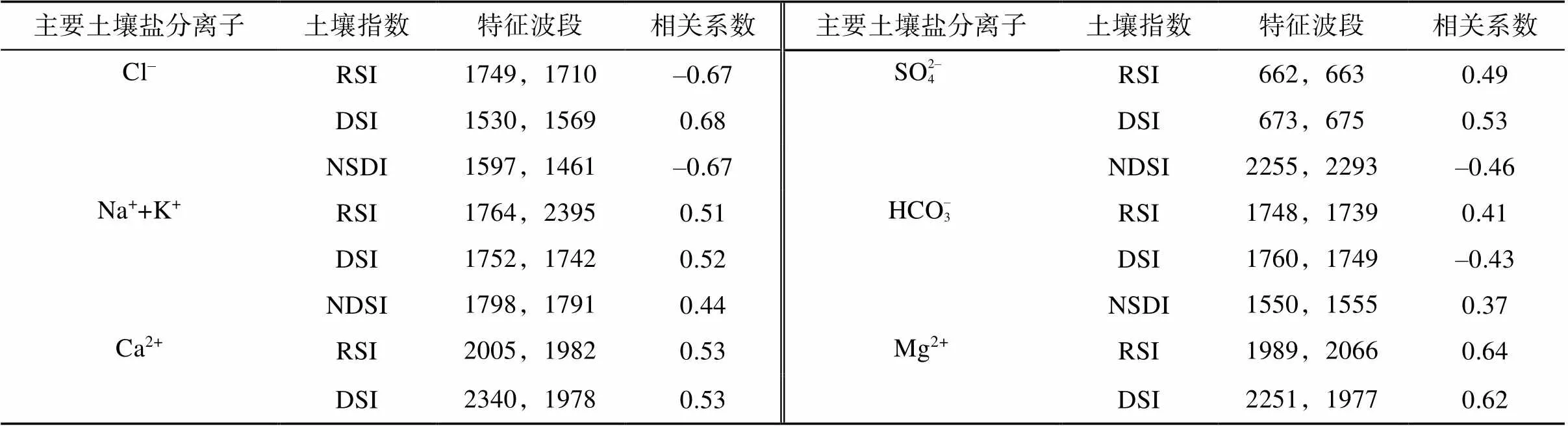
表3 二维指数筛选特征波段

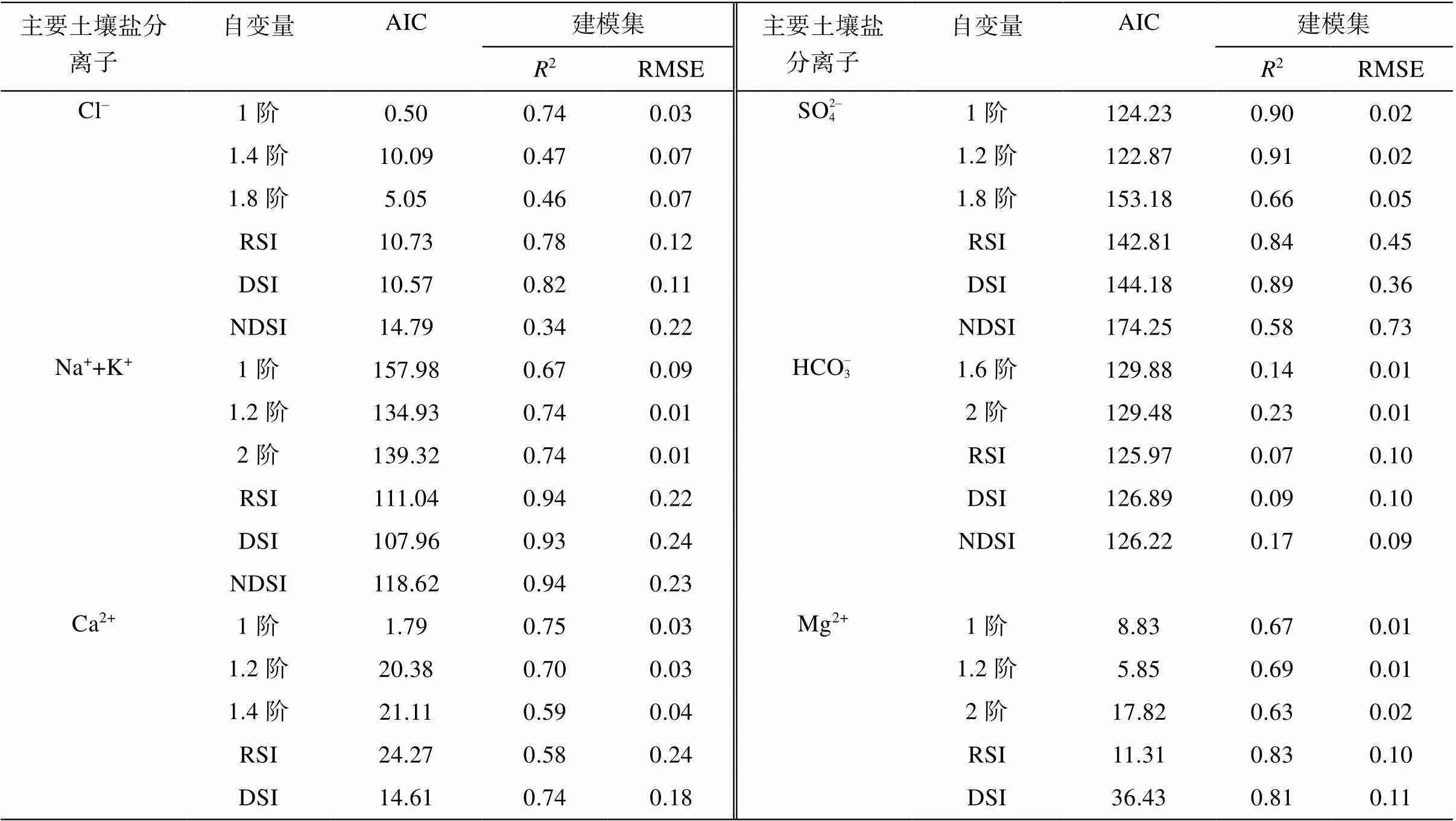
表4 基于GWR模型的建模集

由图4可知估算模型的验证集，对于Cl–而言，基于1阶的2= 0.93，RMSE = 0.11；SO2– 4基于DSI的2= 0.77，RMSE = 0.32；Na++K+基于RSI和DSI的2= 0.74，RMSE = 0.19；HCO– 3基于DSI的2= 0.83，RMSE=0.05；Ca2+基于DSI的2= 0.96，RMSE=0.08；Mg2+基于RSI的2= 0.93，RMSE = 0.08，均为验证集较优模型。综合建模集和验证集来看，Cl–的最优模型是1阶，其中1阶的AIC值为0.50；SO2– 4的最优模型是1.2阶，1.2阶的AIC较小为122.87；Na++K+的最优模型是RSI，AIC最小的是DSI，RSI比DSI的AIC高3.08；Ca2+的最优模型是DSI，其中1阶微分的AIC较小为1.79，DSI在光谱指数中AIC为14.61；Mg2+的最优模型是RSI，RSI的AIC为11.31，比最小的AIC高5.46。从整体来看，选择的最优模型，多是分数阶微分或光谱指数中AIC值较小的模型。Na++K+和Mg2+在二维光谱指数构建的估算模型，建模集和验证集的决定系数均优于一维。

3 讨论

通过优选高光谱的特征波段，对优选的1种特征波段和优选的2种特征波段进行比较，优选的特征波段具有一定重合性，Na++K+特征波段在光谱变换下集中在可见光绿、黄、橙、红光及近红外波段，2种波段选取中重合部分为近红外波段；SO2– 4的特征波段在光谱变换下主要集中在可见光波段，2种波段选取重合部分也为可见光红光和近红外波段；Cl–、Ca2+、Mg2+的特征波段在光谱变化下和2种波段选取中都集中在近红外波段；HCO– 3在光谱变换及指数选取的特征波段分别集中在可见光紫光、蓝光波段和近红外波段。基于GWR模型对于研究区土壤盐分离子估算具有较优的结果。GWR模型对Na++K+估算效果较好，这与宋梦洁和李新国[26]在相同研究区下利用多元线性回归模型估算的分析结果相同。GWR模型能够对Na++K+进行较好的预测，依据梁东等[27]的研究结果，研究区的土壤盐分与Na++K+呈极显著正相关，且Na++K+在不同植被类型中含量都是最高。土壤盐分离子含量较高，可进行很好的预测，这或许也说明光谱反射特征机理是对主要离子组成的响应。土壤盐分离子含量、组成、结合方式的差异，在提取特征波段和光谱构建模型时难度较大。GWR模型提高土壤盐分离子的估算效果受到土壤盐分离子与各变量间相关关系的空间非稳定性程度[28]。本研究的土壤盐分离子估算效果与代希君等[1]在新疆南疆的研究结果基本相同，SO2– 4、Ca2+、Mg2+、Cl–的估算精度较高，对于土壤盐分离子中含量较低的HCO– 3估算精度较低。

4 结论

1)Na++K+的微分变换光谱特征波段主要集中在468 ～ 724 nm与1 182 ～ 1 539 nm，相关性值最大为0.48；二维土壤指数特征波段主要集中在1 742 ～ 2 395 nm；基于RSI的特征波段优选下地理加权回归模型对Na++K+含量的估算效果较好，建模集2= 0.94，RMSE = 0.22，验证集2= 0.74，RMSE = 0.19。

2)SO2– 4的微分变换特征波段主要集中在468 ～ 724 nm，其中在1阶、1.2阶、DSI的建模集和验证集精度2值最大，2值均大于0.71；Ca2+、Mg2+、Cl–的特征波段均在近红外区域，且验证集精度高于建模集精度，其中Ca2+在光谱指数DSI的验证精度2值最大为0.96，RMSE为0.08。

3)基于地理加权回归模型的土壤盐分离子估算的最优模型2值范围在0.74 ～ 0.96，最优模型的AIC值范围在0.50 ～ 122.87；土壤离子中含量相对较高的Na++K+、SO2– 4、Cl–的地理加权回归模型精度高于含量较低的Ca2+、Mg2+。

[1] 代希君, 张艳丽, 彭杰, 等. 土壤水溶性盐基离子的高光谱反演模型及验证[J]. 农业工程学报, 2015, 31(22): 139–145.

[2] Hammam A A, Mohamed E S. Mapping soil salinity in the East Nile Delta using several methodological approaches of salinity assessment[J]. The Egyptian Journal of Remote Sensing and Space Science, 2020, 23(2): 125–131.

[3] Chen K, Li C, Tang R N. Estimation of the nitrogen concentration of rubber tree using fractionalaugmented NIR spectra[J]. Industrial Crops and Products, 2017, 108: 831–839.

[4] Srivastava R, Sethi M, Yadav R K, et al. Visible-near infrared reflectance spectroscopy for rapid characterization of salt-affected soil in the indo-Gangetic Plains of Haryana, India[J]. Journal of the Indian Society of Remote Sensing, 2017, 45(2): 307–315.

[5] 孙亚楠, 李仙岳, 史海滨, 等. 河套灌区土壤水溶性盐基离子高光谱综合反演模型[J]. 农业机械学报, 2019, 50(5): 344–355.

[6] 郭鹏, 李华, 陈红艳, 等. 基于光谱指数优选的土壤盐分定量光谱估测[J]. 水土保持通报, 2018, 38(3): 193–199, 205.

[7] 张俊华, 贾萍萍, 孙媛, 等. 基于高光谱特征的盐渍化土壤不同土层盐分离子含量预测[J]. 农业工程学报, 2019, 35(12): 106–115.

[8] 肖云飞, 高小红, 李冠稳. 土壤有机质可见光–近红外光谱预测样本优化选择[J]. 土壤, 2020, 52(2): 404–413.

[9] 张文文, 杨可明, 夏天, 等. 光谱分数阶微分与玉米叶片重金属铜含量的相关性分析[J]. 科学技术与工程, 2017, 17(25): 33–38.

[10] 亚森江·喀哈尔, 杨胜天, 尼格拉·塔什甫拉提, 等. 基于分数阶微分优化光谱指数的土壤电导率高光谱估算[J]. 生态学报, 2019, 39(19): 7237–7248.

[11] 吾木提·艾山江, 买买提·沙吾提, 马春玥. 基于分数阶微分和连续投影算法-反向传播神经网络的小麦叶片含水量高光谱估算[J]. 激光与光电子学进展, 2019, 56(15): 251–259.

[12] 池涛, 曹广溥, 李丙春, 等. 基于高光谱数据和SVM方法的土壤盐渍度反演[J]. 山东农业大学学报(自然科学版), 2018, 49(4): 585–590.

[13] 刘亚秋, 陈红艳, 王瑞燕, 等. 基于可见/近红外光谱的黄河口区土壤盐分及其主要离子的定量分析[J]. 中国农业科学, 2016, 49(10): 1925–1935.

[14] 袁玉芸, 瓦哈甫·哈力克, 关靖云, 等. 基于GWR模型的于田绿洲土壤表层盐分空间分异及其影响因子[J]. 应用生态学报, 2016, 27(10): 3273–3282.

[15] 巫振富, 赵彦锋, 程道全, 等. 基于地理加权回归的小麦测土配方施肥效果空间分析[J]. 土壤学报, 2019, 56(4): 860–872.

[16] 李志, 李新国, 毛东雷, 等. 博斯腾湖西岸湖滨带不同植被类型土壤剖面盐分特征分析[J]. 西北农业学报, 2018, 27(2): 260–268.

[17] 李新国, 李和平, 任云霞, 等. 开都河流域下游绿洲土壤盐渍化特征及其光谱分析[J]. 土壤通报, 2012, 43(1): 166–170.

[18] 马利芳, 熊黑钢, 张芳. 基于野外VIS-NIR光谱的土壤盐分主要离子预测[J]. 土壤, 2020, 52(1): 188–194.

[19] 张绍阳, 解源源, 张鑫, 等. 基于分数阶微分的模糊交通视频图像增强[J]. 光学精密工程, 2014, 22(3): 779–786.

[20] Tarasov V E. On chain rule for fractional derivatives[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 30(1/2/3): 1–4.

[21] 梁静, 丁建丽, 王敬哲, 等. 基于反射光谱与Landsat 8 OLI多光谱数据的艾比湖湿地土壤盐分估算[J]. 土壤学报, 2019, 56(2): 320–330.

[22] Fotheringham A S, Charlton M E, Brunsdon C. Geographically weighted regression: A natural evolution of the expansion method for spatial data analysis[J]. Environment and Planning A: Economy and Space, 1998, 30(11): 1905–1927.

[23] Abliz A, Tiyip T, Ghulam A, et al. Effects of shallow groundwater table and salinity on soil salt dynamics in the Keriya Oasis, Northwestern China[J]. Environmental Earth Sciences, 2016, 75(3): 1–15.

[24] 赵明松, 刘斌寅, 卢宏亮, 等. 基于地理加权回归的地形平缓区土壤有机质空间建模[J]. 农业工程学报, 2019, 35(20): 102–110.

[25] 袁婕, 张飞, 葛翔宇, 等. 地理加权回归模型结合高光谱反演盐生植物叶片盐离子含量[J]. 农业工程学报, 2019, 35(10): 115–124.

[26] 宋梦洁, 李新国. 博斯腾湖西岸湖滨绿洲芦苇地土壤盐分特征高光谱分析[J]. 扬州大学学报(农业与生命科学版), 2016, 37(1): 75–80.

[27] 梁东, 李新国, 阿斯耶姆·图尔迪, 等. 博斯腾湖西岸湖滨带土壤剖面盐分特征分析[J]. 干旱地区农业研究, 2014, 32(4): 151–158.

[28] 江振蓝, 杨玉盛, 沙晋明. GWR模型在土壤重金属高光谱预测中的应用[J]. 地理学报, 2017, 72(3): 533–544.

Hyperspectral Estimation of Soil Salt Ion Contents in Lakeside Oasis of Bosten Lake Based on Geographical Weighted Regression Model

ZHAO Hui1, 2, LI Xinguo1, 2*, JIN Wangui1, 2, NIU Fangpeng1, 2, MAMATTURSUN·Eziz1, 2

(1 College of Geographic Sciences and Tourism, Xinjiang Normal University, Urumqi 830054, China; 2 Xinjiang Laboratory of Lake Environment and Resources in Arid Zone, Urumqi 830054, China)

In this paper, the lakeside oasis of Bosten Lake was taken as the study area, the contents of main soil salt ions (HCO– 3, Cl–, SO2– 4, Ca2+, Mg2+, Na++K+) were measured, soil hyperspectral reflectance, fractional differential spectral transformation, and 2D soil indexes such as RSI, DSI and NDSI were obtained, and then the estimation models of soil salt ion contents were constructed based on the geographically weighted regression (GWR) model. The results showed that the feature bands of Na++K+were concentrated in 468-724 nm and 1 182-1 539 nm under the differential spectral transformation, and the feature bands of 2D soil indexes were concentrated in the near-infrared band (1 742-2 395 nm). GWR model based on RSI feature band optimization estimated Na++K+content well, in which the modeling set2was 0.94 and RMSE was 0.22, the validation set2was 0.74 and RMSE was 0.19.The optimal band of SO2– 4 content in order 1.2 was 469-636 nm, in which the modeling set2was 0.91 and RMSE was 0.02, the validation set2was 0.75 and RMSE was 0.33.The preferred feature bands of Ca2+and Mg2+were mainly concentrated in the near-infrared band (912-2 340 nm). The modeling effect of the near-infrared band with Cl–content in the first order was better, the modeling set2= 0.74, RMSE = 0.03, verification set2= 0.93, RMSE = 0.11.The accuracies of GWR model of Na++K+, SO2– 4and Cl–with higher contents were higher than those of Ca2+and Mg2+with lower contents.

Soil salt ion; Fractional differentiation; Spectral matrix coefficient map; Geographically weighted regression model; Lakeside oasis

S127

A

10.13758/j.cnki.tr.2021.03.026

赵慧, 李新国, 靳万贵, 等. 基于地理加权回归模型的博斯腾湖湖滨绿洲土壤盐分离子含量高光谱估算. 土壤, 2021, 53(3): 646–653.

国家自然科学基金项目(41661047，U2003301)资助。

(onlinelxg@sina.com)

赵慧(1994—)，女，河南周口人，硕士研究生，主要从事干旱区土壤资源变化及其遥感应用研究。E-mail: ziyuhe528@163.com